JL
Uploaded byJimbo Lamb
PDF, PPTX2,433 views

Geometry Section 5-1 1112

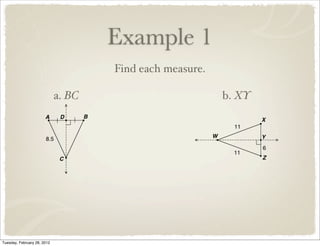
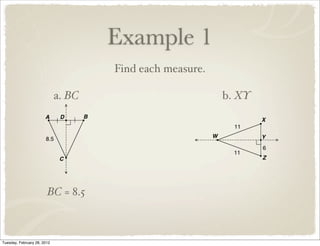
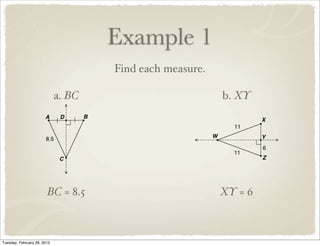
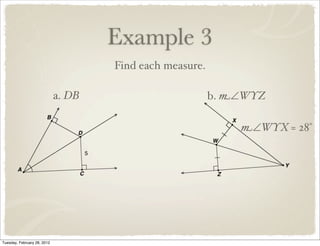
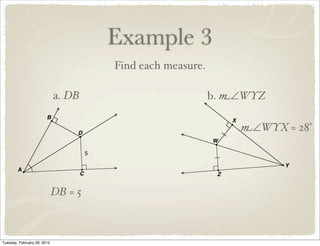
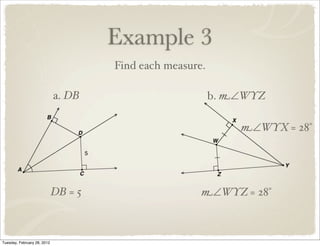
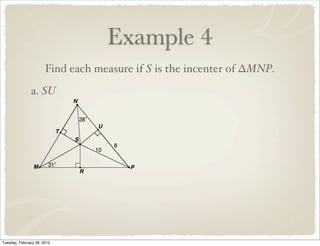
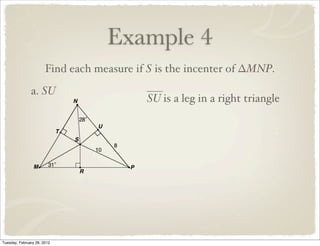
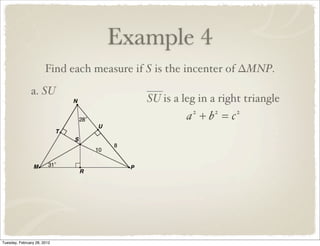
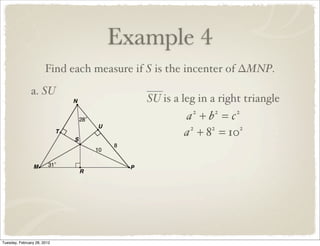
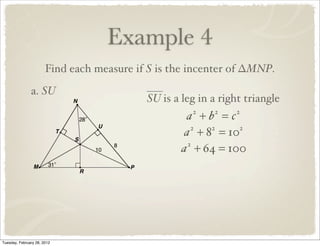
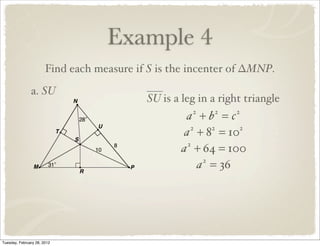
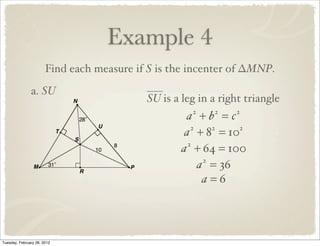
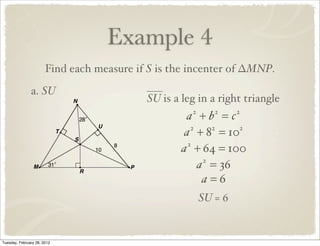
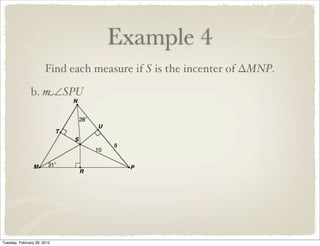
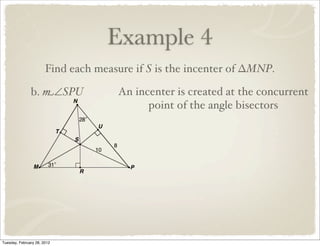
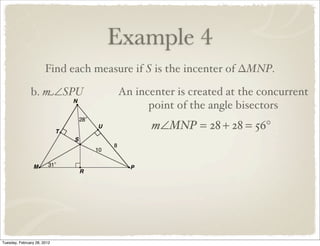
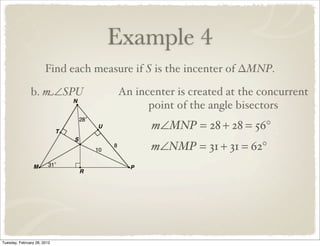
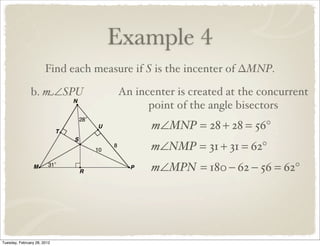
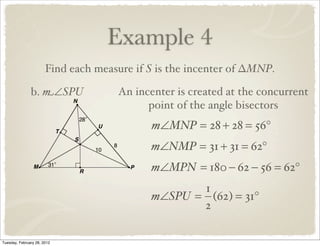
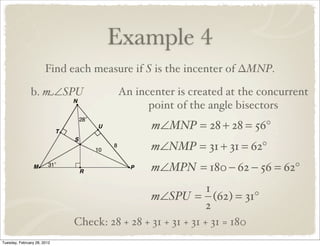
The document discusses bisectors of triangles, including perpendicular bisectors and angle bisectors. It defines key terms like perpendicular bisector, concurrent lines, circumcenter, and incenter. Theorems are presented about the properties of points on perpendicular bisectors, including that they are equidistant from the endpoints of the bisected segment. Similarly, points on angle bisectors are equidistant from the sides of the bisected angle. The circumcenter and incenter are shown to be equidistant from the vertices and sides of a triangle respectively. Examples demonstrate applying the concepts.

Embed presentation

Download as PDF, PPTX
Chapter 5 Relationships in Triangles Tuesday, February 28, 2012
SECTION 5-1 Bisectors of Triangles Tuesday, February 28, 2012
Essential Questions How do you identify and use perpendicular bisectors in triangles? How do you identify and use angle bisectors in triangles? Tuesday, February 28, 2012
Vocabulary 1. Perpendicular Bisector: 2. Concurrent Lines: 3. Point of Concurrency: 4. Circumcenter: 5. Incenter: Tuesday, February 28, 2012
Vocabulary 1. Perpendicular Bisector: A segment that not only cuts another segment in half, but it also forms a 90° angle at the intersection 2. Concurrent Lines: 3. Point of Concurrency: 4. Circumcenter: 5. Incenter: Tuesday, February 28, 2012
Vocabulary 1. Perpendicular Bisector: A segment that not only cuts another segment in half, but it also forms a 90° angle at the intersection 2. Concurrent Lines: Three or more lines that intersect at the same point 3. Point of Concurrency: 4. Circumcenter: 5. Incenter: Tuesday, February 28, 2012
Vocabulary 1. Perpendicular Bisector: A segment that not only cuts another segment in half, but it also forms a 90° angle at the intersection 2. Concurrent Lines: Three or more lines that intersect at the same point 3. Point of Concurrency: The common point where three or more lines intersect 4. Circumcenter: 5. Incenter: Tuesday, February 28, 2012
Vocabulary 1. Perpendicular Bisector: A segment that not only cuts another segment in half, but it also forms a 90° angle at the intersection 2. Concurrent Lines: Three or more lines that intersect at the same point 3. Point of Concurrency: The common point where three or more lines intersect 4. Circumcenter: The concurrent point where the perpendicular bisectors of the sides of a triangle meet 5. Incenter: Tuesday, February 28, 2012
Vocabulary 1. Perpendicular Bisector: A segment that not only cuts another segment in half, but it also forms a 90° angle at the intersection 2. Concurrent Lines: Three or more lines that intersect at the same point 3. Point of Concurrency: The common point where three or more lines intersect 4. Circumcenter: The concurrent point where the perpendicular bisectors of the sides of a triangle meet 5. Incenter: The concurrent point where the angle bisectors of the angles of a triangle meet Tuesday, February 28, 2012
5.1 - Perpendicular Bisector Theorem If a point lies on the perpendicular bisector of a segment, the it is equidistant from the endpoints of the segment Tuesday, February 28, 2012
5.1 - Perpendicular Bisector Theorem If a point lies on the perpendicular bisector of a segment, the it is equidistant from the endpoints of the segment Tuesday, February 28, 2012
5.1 - Perpendicular Bisector Theorem If a point lies on the perpendicular bisector of a segment, the it is equidistant from the endpoints of the segment AC = BC Tuesday, February 28, 2012
5.2 - Converse of the Perpendicular Bisector Theorem If a point is equidistant from the endpoints of a segment, then it is on the perpendicular bisector of the segment Tuesday, February 28, 2012
5.2 - Converse of the Perpendicular Bisector Theorem If a point is equidistant from the endpoints of a segment, then it is on the perpendicular bisector of the segment Tuesday, February 28, 2012
5.2 - Converse of the Perpendicular Bisector Theorem If a point is equidistant from the endpoints of a segment, then it is on the perpendicular bisector of the segment If WX = WZ, then XY = ZY Tuesday, February 28, 2012
5.3 - Circumcenter Theorem The circumcenter (concurrent point where perpendicular bisectors intersect) is equidistant from the vertices of a triangle Tuesday, February 28, 2012
5.3 - Circumcenter Theorem The circumcenter (concurrent point where perpendicular bisectors intersect) is equidistant from the vertices of a triangle Tuesday, February 28, 2012
5.3 - Circumcenter Theorem The circumcenter (concurrent point where perpendicular bisectors intersect) is equidistant from the vertices of a triangle If G is the circumcenter, then GA = GB = GC Tuesday, February 28, 2012
5.4 - Angle Bisector Theorem If a point is on the bisector of an angle, then it is equidistant from the sides of the angle Tuesday, February 28, 2012
5.4 - Angle Bisector Theorem If a point is on the bisector of an angle, then it is equidistant from the sides of the angle Tuesday, February 28, 2012
5.4 - Angle Bisector Theorem If a point is on the bisector of an angle, then it is equidistant from the sides of the angle If AD bisects ∠BAC, BD ⊥ AB, and CD ⊥ AC, then BD = CD Tuesday, February 28, 2012
5.5 - Converse of the Angle Bisector Theorem If a point in the interior of an angle is equidistant from the sides of the angle, then it is on the bisector of the angle Tuesday, February 28, 2012
5.5 - Converse of the Angle Bisector Theorem If a point in the interior of an angle is equidistant from the sides of the angle, then it is on the bisector of the angle Tuesday, February 28, 2012
5.5 - Converse of the Angle Bisector Theorem If a point in the interior of an angle is equidistant from the sides of the angle, then it is on the bisector of the angle If BD ⊥ AB, CD ⊥ AC, and BD = CD, then AD bisects ∠BAC Tuesday, February 28, 2012
5.6 - Incenter Theorem The incenter (concurrent point where angle bisectors meet) is equidistant from each side of the triangle Tuesday, February 28, 2012
5.6 - Incenter Theorem The incenter (concurrent point where angle bisectors meet) is equidistant from each side of the triangle Tuesday, February 28, 2012
5.6 - Incenter Theorem The incenter (concurrent point where angle bisectors meet) is equidistant from each side of the triangle If S is the incenter of ∆MNP, then RS = TS = US Tuesday, February 28, 2012
Example 1 Find each measure. a. BC b. XY Tuesday, February 28, 2012
Example 1 Find each measure. a. BC b. XY BC = 8.5 Tuesday, February 28, 2012
Example 1 Find each measure. a. BC b. XY BC = 8.5 XY = 6 Tuesday, February 28, 2012
Example 1 Find each measure. c. PQ Tuesday, February 28, 2012
Example 1 Find each measure. c. PQ 3x + 1 = 5x − 3 Tuesday, February 28, 2012
Example 1 Find each measure. c. PQ 3x + 1 = 5x − 3 -3x -3x Tuesday, February 28, 2012
Example 1 Find each measure. c. PQ 3x + 1 = 5x − 3 -3x +3 -3x +3 Tuesday, February 28, 2012
Example 1 Find each measure. c. PQ 3x + 1 = 5x − 3 -3x +3 -3x +3 4 = 2x Tuesday, February 28, 2012
Example 1 Find each measure. c. PQ 3x + 1 = 5x − 3 -3x +3 -3x +3 4 = 2x x=2 Tuesday, February 28, 2012
Example 1 Find each measure. c. PQ 3x + 1 = 5x − 3 PQ = 3x + 1 -3x +3 -3x +3 4 = 2x x=2 Tuesday, February 28, 2012
Example 1 Find each measure. c. PQ 3x + 1 = 5x − 3 PQ = 3x + 1 -3x +3 -3x +3 PQ = 3(2) + 1 4 = 2x x=2 Tuesday, February 28, 2012
Example 1 Find each measure. c. PQ 3x + 1 = 5x − 3 PQ = 3x + 1 -3x +3 -3x +3 PQ = 3(2) + 1 4 = 2x PQ = 6 + 1 x=2 Tuesday, February 28, 2012
Example 1 Find each measure. c. PQ 3x + 1 = 5x − 3 PQ = 3x + 1 -3x +3 -3x +3 PQ = 3(2) + 1 4 = 2x PQ = 6 + 1 x=2 PQ = 7 Tuesday, February 28, 2012
Example 2 A triangular shaped garden is shown. Can a fountain be placed at the circumcenter and still be in the garden? Tuesday, February 28, 2012
Example 2 A triangular shaped garden is shown. Can a fountain be placed at the circumcenter and still be in the garden? Tuesday, February 28, 2012
Example 2 A triangular shaped garden is shown. Can a fountain be placed at the circumcenter and still be in the garden? No, it cannot Tuesday, February 28, 2012
Question If you have an obtuse triangle, where will the circumcenter be? If you have an acute triangle, where will the circumcenter be? If you have an right triangle, where will the circumcenter be? Tuesday, February 28, 2012
Question If you have an obtuse triangle, where will the circumcenter be? It will be outside the triangle If you have an acute triangle, where will the circumcenter be? If you have an right triangle, where will the circumcenter be? Tuesday, February 28, 2012
Question If you have an obtuse triangle, where will the circumcenter be? It will be outside the triangle If you have an acute triangle, where will the circumcenter be? It will be inside the triangle If you have an right triangle, where will the circumcenter be? Tuesday, February 28, 2012
Question If you have an obtuse triangle, where will the circumcenter be? It will be outside the triangle If you have an acute triangle, where will the circumcenter be? It will be inside the triangle If you have an right triangle, where will the circumcenter be? It will be on the hypotenuse of the triangle Tuesday, February 28, 2012
Example 3 Find each measure. a. DB b. m∠WYZ m∠WYX = 28° Tuesday, February 28, 2012
Example 3 Find each measure. a. DB b. m∠WYZ m∠WYX = 28° DB = 5 Tuesday, February 28, 2012
Example 3 Find each measure. a. DB b. m∠WYZ m∠WYX = 28° DB = 5 m∠WYZ = 28° Tuesday, February 28, 2012
Example 3 Find each measure. c. QS Tuesday, February 28, 2012
Example 3 Find each measure. c. QS 4x - 1 = 3x + 2 Tuesday, February 28, 2012
Example 3 Find each measure. c. QS 4x - 1 = 3x + 2 -3x -3x Tuesday, February 28, 2012
Example 3 Find each measure. c. QS 4x - 1 = 3x + 2 -3x +1 -3x +1 Tuesday, February 28, 2012
Example 3 Find each measure. c. QS 4x - 1 = 3x + 2 -3x +1 -3x +1 x=3 Tuesday, February 28, 2012
Example 3 Find each measure. c. QS 4x - 1 = 3x + 2 QS = 4x - 1 -3x +1 -3x +1 x=3 Tuesday, February 28, 2012
Example 3 Find each measure. c. QS 4x - 1 = 3x + 2 QS = 4x - 1 -3x +1 -3x +1 QS = 4(3) - 1 x=3 Tuesday, February 28, 2012
Example 3 Find each measure. c. QS 4x - 1 = 3x + 2 QS = 4x - 1 -3x +1 -3x +1 QS = 4(3) - 1 x=3 QS = 12 - 1 Tuesday, February 28, 2012
Example 3 Find each measure. c. QS 4x - 1 = 3x + 2 QS = 4x - 1 -3x +1 -3x +1 QS = 4(3) - 1 x=3 QS = 12 - 1 QS = 11 Tuesday, February 28, 2012
Example 4 Find each measure if S is the incenter of ∆MNP. a. SU Tuesday, February 28, 2012
Example 4 Find each measure if S is the incenter of ∆MNP. a. SU SU is a leg in a right triangle Tuesday, February 28, 2012
Example 4 Find each measure if S is the incenter of ∆MNP. a. SU SU is a leg in a right triangle a +b =c 2 2 2 Tuesday, February 28, 2012
Example 4 Find each measure if S is the incenter of ∆MNP. a. SU SU is a leg in a right triangle a +b =c 2 2 2 a + 8 = 10 2 2 2 Tuesday, February 28, 2012
Example 4 Find each measure if S is the incenter of ∆MNP. a. SU SU is a leg in a right triangle a +b =c 2 2 2 a + 8 = 10 2 2 2 a + 64 = 100 2 Tuesday, February 28, 2012
Example 4 Find each measure if S is the incenter of ∆MNP. a. SU SU is a leg in a right triangle a +b =c 2 2 2 a + 8 = 10 2 2 2 a + 64 = 100 2 a = 36 2 Tuesday, February 28, 2012
Example 4 Find each measure if S is the incenter of ∆MNP. a. SU SU is a leg in a right triangle a +b =c 2 2 2 a + 8 = 10 2 2 2 a + 64 = 100 2 a = 36 2 a=6 Tuesday, February 28, 2012
Example 4 Find each measure if S is the incenter of ∆MNP. a. SU SU is a leg in a right triangle a +b =c 2 2 2 a + 8 = 10 2 2 2 a + 64 = 100 2 a = 36 2 a=6 SU = 6 Tuesday, February 28, 2012
Example 4 Find each measure if S is the incenter of ∆MNP. b. m∠SPU Tuesday, February 28, 2012
Example 4 Find each measure if S is the incenter of ∆MNP. b. m∠SPU An incenter is created at the concurrent point of the angle bisectors Tuesday, February 28, 2012
Example 4 Find each measure if S is the incenter of ∆MNP. b. m∠SPU An incenter is created at the concurrent point of the angle bisectors m∠MNP = 28 + 28 = 56° Tuesday, February 28, 2012
Example 4 Find each measure if S is the incenter of ∆MNP. b. m∠SPU An incenter is created at the concurrent point of the angle bisectors m∠MNP = 28 + 28 = 56° m∠NMP = 31 + 31 = 62° Tuesday, February 28, 2012
Example 4 Find each measure if S is the incenter of ∆MNP. b. m∠SPU An incenter is created at the concurrent point of the angle bisectors m∠MNP = 28 + 28 = 56° m∠NMP = 31 + 31 = 62° m∠MPN = 180 − 62 − 56 = 62° Tuesday, February 28, 2012
Example 4 Find each measure if S is the incenter of ∆MNP. b. m∠SPU An incenter is created at the concurrent point of the angle bisectors m∠MNP = 28 + 28 = 56° m∠NMP = 31 + 31 = 62° m∠MPN = 180 − 62 − 56 = 62° 1 m∠SPU = (62) = 31° 2 Tuesday, February 28, 2012
Example 4 Find each measure if S is the incenter of ∆MNP. b. m∠SPU An incenter is created at the concurrent point of the angle bisectors m∠MNP = 28 + 28 = 56° m∠NMP = 31 + 31 = 62° m∠MPN = 180 − 62 − 56 = 62° 1 m∠SPU = (62) = 31° 2 Check: 28 + 28 + 31 + 31 + 31 + 31 = 180 Tuesday, February 28, 2012
Check Your Understading Make sure to review p. 327 #1-8 Tuesday, February 28, 2012
Problem Set Tuesday, February 28, 2012
Problem Set p. 327 #9-29 odd, 48 "Great opportunities to help others seldom come, but small ones surround us every day." - Sally Koch Tuesday, February 28, 2012

More Related Content

PDF
Geometry section 4-1 1112
byJimbo Lamb
 
PDF
Geometry Section 3-5 1112
byJimbo Lamb
 
PPT
1.1 sets, statements, and reasoning
bysadhwani37
 
PDF
Geometry Section 5-3 11-12
byJimbo Lamb
 
PDF
Geometry Section 4-3
byJimbo Lamb
 
PDF
Geometry Section 6-4 1112
byJimbo Lamb
 
PDF
Geometry Section 4-6 1112
byJimbo Lamb
 
PDF
Geometry Section 5-4 1112
byJimbo Lamb
 
Geometry section 4-1 1112
byJimbo Lamb
 
Geometry Section 3-5 1112
byJimbo Lamb
 
1.1 sets, statements, and reasoning
bysadhwani37
 
Geometry Section 5-3 11-12
byJimbo Lamb
 
Geometry Section 4-3
byJimbo Lamb
 
Geometry Section 6-4 1112
byJimbo Lamb
 
Geometry Section 4-6 1112
byJimbo Lamb
 
Geometry Section 5-4 1112
byJimbo Lamb
 

Viewers also liked

PDF
Geometry Section 3-1 1112
byJimbo Lamb
 
PDF
Geometry Section 3-6 1112
byJimbo Lamb
 
PDF
Geometry Section 6-2 1112
byJimbo Lamb
 
PDF
Geometry Section 3-3 1112
byJimbo Lamb
 
PDF
Geometry Section 3-2 1112
byJimbo Lamb
 
PDF
Geometry Section 3-4 1112
byJimbo Lamb
 
PDF
Geometry Section 5-2 1112
byJimbo Lamb
 
PDF
Geometry Section 6-1 1112
byJimbo Lamb
 
PDF
Geometry Section 4-5 1112
byJimbo Lamb
 
PDF
Geometry Section 6-5 1112
byJimbo Lamb
 
PDF
Geometry Section 4-2
byJimbo Lamb
 
PDF
Geometry Section 6-6 1112
byJimbo Lamb
 
PDF
Geometry Section 6-3 1112
byJimbo Lamb
 
PDF
Geometry Section 2-8 1112
byJimbo Lamb
 
PDF
Geometry Section 2-3 1112
byJimbo Lamb
 
PDF
Geometry Section 5-5 1112
byJimbo Lamb
 
PDF
Geometry Section 2-7 1112
byJimbo Lamb
 
PDF
Geometry Section 2-5 1112
byJimbo Lamb
 
PDF
Geometry Section 2-2 1112
byJimbo Lamb
 
PDF
Geometry Section 2-6
byJimbo Lamb
 
Geometry Section 3-1 1112
byJimbo Lamb
 
Geometry Section 3-6 1112
byJimbo Lamb
 
Geometry Section 6-2 1112
byJimbo Lamb
 
Geometry Section 3-3 1112
byJimbo Lamb
 
Geometry Section 3-2 1112
byJimbo Lamb
 
Geometry Section 3-4 1112
byJimbo Lamb
 
Geometry Section 5-2 1112
byJimbo Lamb
 
Geometry Section 6-1 1112
byJimbo Lamb
 
Geometry Section 4-5 1112
byJimbo Lamb
 
Geometry Section 6-5 1112
byJimbo Lamb
 
Geometry Section 4-2
byJimbo Lamb
 
Geometry Section 6-6 1112
byJimbo Lamb
 
Geometry Section 6-3 1112
byJimbo Lamb
 
Geometry Section 2-8 1112
byJimbo Lamb
 
Geometry Section 2-3 1112
byJimbo Lamb
 
Geometry Section 5-5 1112
byJimbo Lamb
 
Geometry Section 2-7 1112
byJimbo Lamb
 
Geometry Section 2-5 1112
byJimbo Lamb
 
Geometry Section 2-2 1112
byJimbo Lamb
 
Geometry Section 2-6
byJimbo Lamb
 

Similar to Geometry Section 5-1 1112

PDF
Obj. 20 Perpendicular and Angle Bisectors
bysmiller5
 
PPT
5.2 terms
bytommy34g
 
PPTX
Perpendicular Bisectors in Triangles.pptx
byAteeqRehman86
 
PPTX
Perpendicular Bisectors in Triangles.pptx
byAteeqRehman86
 
PPT
Geom 5point1and2
byherbison
 
PPT
5.2 bisectors of a triangle
byRobert Hammarstrand
 
PDF
2.5.6 Perpendicular and Angle Bisectors
bysmiller5
 
PDF
2.5.5 Perpendicular and Angle Bisectors
bysmiller5
 
PPTX
Sec. 5.2.pptxkkkkjjjjjjjjjjjjjjjjjjjjjjjj
byperjgalio
 
PPT
5.1 terms
bytommy34g
 
PPT
Chapter_5_Organizer_Properties_ofTriangles.ppt
byJenieDimarucut1
 
PPTX
5-2 Perpendicular and Angle Bisectors.pptx
byInactiveBear838
 
PPTX
perpendicular lines-lesson in mathematics8.pptx
byAngelFaithBactol
 
PPT
Geometry unit 5.3
byMark Ryder
 
PDF
4.5 Special Segments in Triangles
bysmiller5
 
PPT
Geometry 201 unit 5.3
byMark Ryder
 
PPTX
mathematics 8 Q4 proving ANGLE BISECTOR.pptx
byFranklinPaira
 
PPTX
Quarter 4 week 4day 2Mathematics Grade 8 PPT
byRica Mae Morales Rosete
 
PDF
Geometry mell2010
byTexas State University
 
PPT
Perpendicular_and_Angle_Bisector_Activity_Lesson.ppt
byLailaVispoBalinado
 
Obj. 20 Perpendicular and Angle Bisectors
bysmiller5
 
5.2 terms
bytommy34g
 
Perpendicular Bisectors in Triangles.pptx
byAteeqRehman86
 
Perpendicular Bisectors in Triangles.pptx
byAteeqRehman86
 
Geom 5point1and2
byherbison
 
5.2 bisectors of a triangle
byRobert Hammarstrand
 
2.5.6 Perpendicular and Angle Bisectors
bysmiller5
 
2.5.5 Perpendicular and Angle Bisectors
bysmiller5
 
Sec. 5.2.pptxkkkkjjjjjjjjjjjjjjjjjjjjjjjj
byperjgalio
 
5.1 terms
bytommy34g
 
Chapter_5_Organizer_Properties_ofTriangles.ppt
byJenieDimarucut1
 
5-2 Perpendicular and Angle Bisectors.pptx
byInactiveBear838
 
perpendicular lines-lesson in mathematics8.pptx
byAngelFaithBactol
 
Geometry unit 5.3
byMark Ryder
 
4.5 Special Segments in Triangles
bysmiller5
 
Geometry 201 unit 5.3
byMark Ryder
 
mathematics 8 Q4 proving ANGLE BISECTOR.pptx
byFranklinPaira
 
Quarter 4 week 4day 2Mathematics Grade 8 PPT
byRica Mae Morales Rosete
 
Geometry mell2010
byTexas State University
 
Perpendicular_and_Angle_Bisector_Activity_Lesson.ppt
byLailaVispoBalinado
 

More from Jimbo Lamb

PDF
Geometry Section 1-5
byJimbo Lamb
 
PDF
Geometry Section 1-4
byJimbo Lamb
 
PDF
Geometry Section 1-3
byJimbo Lamb
 
PDF
Geometry Section 1-2
byJimbo Lamb
 
PDF
Geometry Section 1-2
byJimbo Lamb
 
PDF
Geometry Section 1-1
byJimbo Lamb
 
PDF
Algebra 2 Section 5-3
byJimbo Lamb
 
PDF
Algebra 2 Section 5-2
byJimbo Lamb
 
PDF
Algebra 2 Section 5-1
byJimbo Lamb
 
PDF
Algebra 2 Section 4-9
byJimbo Lamb
 
PDF
Algebra 2 Section 4-8
byJimbo Lamb
 
PDF
Algebra 2 Section 4-6
byJimbo Lamb
 
PDF
Geometry Section 6-6
byJimbo Lamb
 
PDF
Geometry Section 6-5
byJimbo Lamb
 
PDF
Geometry Section 6-4
byJimbo Lamb
 
PDF
Geometry Section 6-3
byJimbo Lamb
 
PDF
Geometry Section 6-2
byJimbo Lamb
 
PDF
Geometry Section 6-1
byJimbo Lamb
 
PDF
Algebra 2 Section 4-5
byJimbo Lamb
 
PDF
Algebra 2 Section 4-4
byJimbo Lamb
 
Geometry Section 1-5
byJimbo Lamb
 
Geometry Section 1-4
byJimbo Lamb
 
Geometry Section 1-3
byJimbo Lamb
 
Geometry Section 1-2
byJimbo Lamb
 
Geometry Section 1-2
byJimbo Lamb
 
Geometry Section 1-1
byJimbo Lamb
 
Algebra 2 Section 5-3
byJimbo Lamb
 
Algebra 2 Section 5-2
byJimbo Lamb
 
Algebra 2 Section 5-1
byJimbo Lamb
 
Algebra 2 Section 4-9
byJimbo Lamb
 
Algebra 2 Section 4-8
byJimbo Lamb
 
Algebra 2 Section 4-6
byJimbo Lamb
 
Geometry Section 6-6
byJimbo Lamb
 
Geometry Section 6-5
byJimbo Lamb
 
Geometry Section 6-4
byJimbo Lamb
 
Geometry Section 6-3
byJimbo Lamb
 
Geometry Section 6-2
byJimbo Lamb
 
Geometry Section 6-1
byJimbo Lamb
 
Algebra 2 Section 4-5
byJimbo Lamb
 
Algebra 2 Section 4-4
byJimbo Lamb
 

Recently uploaded

PDF
AI Is a Tool, Not a Voice: Radio, Trust, and the Human Factor
byN.A. Shah Ansari
 
PPTX
Greengnorance Toolkit Module 3 Shopping and Food
byKarl Donert
 
PDF
Family and Marriage __ Sociology __ Jhasketan Kuanar __ NURSING VIBE ONLY .pdf
byJK NURSING VIBES ONLY JHASKETAN KUANAR
 
PPTX
Greengnorance Toolkit Module1 Climate Change
byKarl Donert
 
PPTX
Plant fibres used as surgical dressings & Sutures – Surgical Catgut and Ligat...
bySai Meer College of Pharmacy
 
PPTX
Math 8 Quarter 4 Week 4-SECONDARY DATA.pptx
byshahanieabbat3
 
PPTX
Greengnorance Toolkit Module 5 Waste Management
byKarl Donert
 
PPTX
Fluorimetric Analysis- Theory, Instrumentation and Application
bySayali Powar
 
PPTX
How to perform product search based on a custom field from the Website Shop p...
byCeline George
 
PDF
Pratishta Educational Society., Courses & Opportunities
byGanapathiVankudoth
 
PPTX
How to Manage Reservation Method in Odoo 18 Inventory
byCeline George
 
PDF
Conservation of Earthen Structures in India Preserving Traditional and Sustai...
byAman Kumar Singh
 
PDF
Chapter 05 Drugs Acting on the Central Nervous System: Anticonvulsant (Antiep...
bySandeshSul
 
PDF
BP502T Industrial Pharmacy I (Theory) UNIT– I (Part 1)
byRushi Mandali
 
PDF
How "Raiders of the Lost Ark" and "Ordinary People" Employ Non-Verbal Acting
by6x5csns4pn
 
PDF
Workshop 29 Crystal Review All Students by YogiGoddess
by©LDMMIA, ©Reiki Yoga
 
PPTX
How to Track & Manage My Time Section in Odoo 18 Time Off
byCeline George
 
PPTX
Overview of How to set priority in Odoo 19 Todo
byCeline George
 
PDF
java full stack programming and interview questions
byrajuashokit
 
PDF
PHARMACOLOGY 1 ( BP 404 T) Unit 1 (Cology 1)
byChetan Mali
 
AI Is a Tool, Not a Voice: Radio, Trust, and the Human Factor
byN.A. Shah Ansari
 
Greengnorance Toolkit Module 3 Shopping and Food
byKarl Donert
 
Family and Marriage __ Sociology __ Jhasketan Kuanar __ NURSING VIBE ONLY .pdf
byJK NURSING VIBES ONLY JHASKETAN KUANAR
 
Greengnorance Toolkit Module1 Climate Change
byKarl Donert
 
Plant fibres used as surgical dressings & Sutures – Surgical Catgut and Ligat...
bySai Meer College of Pharmacy
 
Math 8 Quarter 4 Week 4-SECONDARY DATA.pptx
byshahanieabbat3
 
Greengnorance Toolkit Module 5 Waste Management
byKarl Donert
 
Fluorimetric Analysis- Theory, Instrumentation and Application
bySayali Powar
 
How to perform product search based on a custom field from the Website Shop p...
byCeline George
 
Pratishta Educational Society., Courses & Opportunities
byGanapathiVankudoth
 
How to Manage Reservation Method in Odoo 18 Inventory
byCeline George
 
Conservation of Earthen Structures in India Preserving Traditional and Sustai...
byAman Kumar Singh
 
Chapter 05 Drugs Acting on the Central Nervous System: Anticonvulsant (Antiep...
bySandeshSul
 
BP502T Industrial Pharmacy I (Theory) UNIT– I (Part 1)
byRushi Mandali
 
How "Raiders of the Lost Ark" and "Ordinary People" Employ Non-Verbal Acting
by6x5csns4pn
 
Workshop 29 Crystal Review All Students by YogiGoddess
by©LDMMIA, ©Reiki Yoga
 
How to Track & Manage My Time Section in Odoo 18 Time Off
byCeline George
 
Overview of How to set priority in Odoo 19 Todo
byCeline George
 
java full stack programming and interview questions
byrajuashokit
 
PHARMACOLOGY 1 ( BP 404 T) Unit 1 (Cology 1)
byChetan Mali
 

Geometry Section 5-1 1112

  • 1.
    Chapter 5 Relationships in Triangles Tuesday, February 28, 2012
  • 2.
    SECTION 5-1 Bisectors of Triangles Tuesday, February 28, 2012
  • 3.
    Essential Questions How do you identify and use perpendicular bisectors in triangles? How do you identify and use angle bisectors in triangles? Tuesday, February 28, 2012
  • 4.
    Vocabulary 1. Perpendicular Bisector: 2. Concurrent Lines: 3. Point of Concurrency: 4. Circumcenter: 5. Incenter: Tuesday, February 28, 2012
  • 5.
    Vocabulary 1. Perpendicular Bisector: A segment that not only cuts another segment in half, but it also forms a 90° angle at the intersection 2. Concurrent Lines: 3. Point of Concurrency: 4. Circumcenter: 5. Incenter: Tuesday, February 28, 2012
  • 6.
    Vocabulary 1. Perpendicular Bisector: A segment that not only cuts another segment in half, but it also forms a 90° angle at the intersection 2. Concurrent Lines: Three or more lines that intersect at the same point 3. Point of Concurrency: 4. Circumcenter: 5. Incenter: Tuesday, February 28, 2012
  • 7.
    Vocabulary 1. Perpendicular Bisector: A segment that not only cuts another segment in half, but it also forms a 90° angle at the intersection 2. Concurrent Lines: Three or more lines that intersect at the same point 3. Point of Concurrency: The common point where three or more lines intersect 4. Circumcenter: 5. Incenter: Tuesday, February 28, 2012
  • 8.
    Vocabulary 1. Perpendicular Bisector: A segment that not only cuts another segment in half, but it also forms a 90° angle at the intersection 2. Concurrent Lines: Three or more lines that intersect at the same point 3. Point of Concurrency: The common point where three or more lines intersect 4. Circumcenter: The concurrent point where the perpendicular bisectors of the sides of a triangle meet 5. Incenter: Tuesday, February 28, 2012
  • 9.
    Vocabulary 1. Perpendicular Bisector: A segment that not only cuts another segment in half, but it also forms a 90° angle at the intersection 2. Concurrent Lines: Three or more lines that intersect at the same point 3. Point of Concurrency: The common point where three or more lines intersect 4. Circumcenter: The concurrent point where the perpendicular bisectors of the sides of a triangle meet 5. Incenter: The concurrent point where the angle bisectors of the angles of a triangle meet Tuesday, February 28, 2012
  • 10.
    5.1 - PerpendicularBisector Theorem If a point lies on the perpendicular bisector of a segment, the it is equidistant from the endpoints of the segment Tuesday, February 28, 2012
  • 11.
    5.1 - PerpendicularBisector Theorem If a point lies on the perpendicular bisector of a segment, the it is equidistant from the endpoints of the segment Tuesday, February 28, 2012
  • 12.
    5.1 - PerpendicularBisector Theorem If a point lies on the perpendicular bisector of a segment, the it is equidistant from the endpoints of the segment AC = BC Tuesday, February 28, 2012
  • 13.
    5.2 - Converseof the Perpendicular Bisector Theorem If a point is equidistant from the endpoints of a segment, then it is on the perpendicular bisector of the segment Tuesday, February 28, 2012
  • 14.
    5.2 - Converseof the Perpendicular Bisector Theorem If a point is equidistant from the endpoints of a segment, then it is on the perpendicular bisector of the segment Tuesday, February 28, 2012
  • 15.
    5.2 - Converseof the Perpendicular Bisector Theorem If a point is equidistant from the endpoints of a segment, then it is on the perpendicular bisector of the segment If WX = WZ, then XY = ZY Tuesday, February 28, 2012
  • 16.
    5.3 - Circumcenter Theorem The circumcenter (concurrent point where perpendicular bisectors intersect) is equidistant from the vertices of a triangle Tuesday, February 28, 2012
  • 17.
    5.3 - Circumcenter Theorem The circumcenter (concurrent point where perpendicular bisectors intersect) is equidistant from the vertices of a triangle Tuesday, February 28, 2012
  • 18.
    5.3 - Circumcenter Theorem The circumcenter (concurrent point where perpendicular bisectors intersect) is equidistant from the vertices of a triangle If G is the circumcenter, then GA = GB = GC Tuesday, February 28, 2012
  • 19.
    5.4 - AngleBisector Theorem If a point is on the bisector of an angle, then it is equidistant from the sides of the angle Tuesday, February 28, 2012
  • 20.
    5.4 - AngleBisector Theorem If a point is on the bisector of an angle, then it is equidistant from the sides of the angle Tuesday, February 28, 2012
  • 21.
    5.4 - AngleBisector Theorem If a point is on the bisector of an angle, then it is equidistant from the sides of the angle If AD bisects ∠BAC, BD ⊥ AB, and CD ⊥ AC, then BD = CD Tuesday, February 28, 2012
  • 22.
    5.5 - Converseof the Angle Bisector Theorem If a point in the interior of an angle is equidistant from the sides of the angle, then it is on the bisector of the angle Tuesday, February 28, 2012
  • 23.
    5.5 - Converseof the Angle Bisector Theorem If a point in the interior of an angle is equidistant from the sides of the angle, then it is on the bisector of the angle Tuesday, February 28, 2012
  • 24.
    5.5 - Converseof the Angle Bisector Theorem If a point in the interior of an angle is equidistant from the sides of the angle, then it is on the bisector of the angle If BD ⊥ AB, CD ⊥ AC, and BD = CD, then AD bisects ∠BAC Tuesday, February 28, 2012
  • 25.
    5.6 - IncenterTheorem The incenter (concurrent point where angle bisectors meet) is equidistant from each side of the triangle Tuesday, February 28, 2012
  • 26.
    5.6 - IncenterTheorem The incenter (concurrent point where angle bisectors meet) is equidistant from each side of the triangle Tuesday, February 28, 2012
  • 27.
    5.6 - IncenterTheorem The incenter (concurrent point where angle bisectors meet) is equidistant from each side of the triangle If S is the incenter of ∆MNP, then RS = TS = US Tuesday, February 28, 2012
  • 28.
    Example 1 Find each measure. a. BC b. XY Tuesday, February 28, 2012
  • 29.
    Example 1 Find each measure. a. BC b. XY BC = 8.5 Tuesday, February 28, 2012
  • 30.
    Example 1 Find each measure. a. BC b. XY BC = 8.5 XY = 6 Tuesday, February 28, 2012
  • 31.
    Example 1 Find each measure. c. PQ Tuesday, February 28, 2012
  • 32.
    Example 1 Find each measure. c. PQ 3x + 1 = 5x − 3 Tuesday, February 28, 2012
  • 33.
    Example 1 Find each measure. c. PQ 3x + 1 = 5x − 3 -3x -3x Tuesday, February 28, 2012
  • 34.
    Example 1 Find each measure. c. PQ 3x + 1 = 5x − 3 -3x +3 -3x +3 Tuesday, February 28, 2012
  • 35.
    Example 1 Find each measure. c. PQ 3x + 1 = 5x − 3 -3x +3 -3x +3 4 = 2x Tuesday, February 28, 2012
  • 36.
    Example 1 Find each measure. c. PQ 3x + 1 = 5x − 3 -3x +3 -3x +3 4 = 2x x=2 Tuesday, February 28, 2012
  • 37.
    Example 1 Find each measure. c. PQ 3x + 1 = 5x − 3 PQ = 3x + 1 -3x +3 -3x +3 4 = 2x x=2 Tuesday, February 28, 2012
  • 38.
    Example 1 Find each measure. c. PQ 3x + 1 = 5x − 3 PQ = 3x + 1 -3x +3 -3x +3 PQ = 3(2) + 1 4 = 2x x=2 Tuesday, February 28, 2012
  • 39.
    Example 1 Find each measure. c. PQ 3x + 1 = 5x − 3 PQ = 3x + 1 -3x +3 -3x +3 PQ = 3(2) + 1 4 = 2x PQ = 6 + 1 x=2 Tuesday, February 28, 2012
  • 40.
    Example 1 Find each measure. c. PQ 3x + 1 = 5x − 3 PQ = 3x + 1 -3x +3 -3x +3 PQ = 3(2) + 1 4 = 2x PQ = 6 + 1 x=2 PQ = 7 Tuesday, February 28, 2012
  • 41.
    Example 2 A triangular shaped garden is shown. Can a fountain be placed at the circumcenter and still be in the garden? Tuesday, February 28, 2012
  • 42.
    Example 2 A triangular shaped garden is shown. Can a fountain be placed at the circumcenter and still be in the garden? Tuesday, February 28, 2012
  • 43.
    Example 2 A triangular shaped garden is shown. Can a fountain be placed at the circumcenter and still be in the garden? No, it cannot Tuesday, February 28, 2012
  • 44.
    Question If you have an obtuse triangle, where will the circumcenter be? If you have an acute triangle, where will the circumcenter be? If you have an right triangle, where will the circumcenter be? Tuesday, February 28, 2012
  • 45.
    Question If you have an obtuse triangle, where will the circumcenter be? It will be outside the triangle If you have an acute triangle, where will the circumcenter be? If you have an right triangle, where will the circumcenter be? Tuesday, February 28, 2012
  • 46.
    Question If you have an obtuse triangle, where will the circumcenter be? It will be outside the triangle If you have an acute triangle, where will the circumcenter be? It will be inside the triangle If you have an right triangle, where will the circumcenter be? Tuesday, February 28, 2012
  • 47.
    Question If you have an obtuse triangle, where will the circumcenter be? It will be outside the triangle If you have an acute triangle, where will the circumcenter be? It will be inside the triangle If you have an right triangle, where will the circumcenter be? It will be on the hypotenuse of the triangle Tuesday, February 28, 2012
  • 48.
    Example 3 Find each measure. a. DB b. m∠WYZ m∠WYX = 28° Tuesday, February 28, 2012
  • 49.
    Example 3 Find each measure. a. DB b. m∠WYZ m∠WYX = 28° DB = 5 Tuesday, February 28, 2012
  • 50.
    Example 3 Find each measure. a. DB b. m∠WYZ m∠WYX = 28° DB = 5 m∠WYZ = 28° Tuesday, February 28, 2012
  • 51.
    Example 3 Find each measure. c. QS Tuesday, February 28, 2012
  • 52.
    Example 3 Find each measure. c. QS 4x - 1 = 3x + 2 Tuesday, February 28, 2012
  • 53.
    Example 3 Find each measure. c. QS 4x - 1 = 3x + 2 -3x -3x Tuesday, February 28, 2012
  • 54.
    Example 3 Find each measure. c. QS 4x - 1 = 3x + 2 -3x +1 -3x +1 Tuesday, February 28, 2012
  • 55.
    Example 3 Find each measure. c. QS 4x - 1 = 3x + 2 -3x +1 -3x +1 x=3 Tuesday, February 28, 2012
  • 56.
    Example 3 Find each measure. c. QS 4x - 1 = 3x + 2 QS = 4x - 1 -3x +1 -3x +1 x=3 Tuesday, February 28, 2012
  • 57.
    Example 3 Find each measure. c. QS 4x - 1 = 3x + 2 QS = 4x - 1 -3x +1 -3x +1 QS = 4(3) - 1 x=3 Tuesday, February 28, 2012
  • 58.
    Example 3 Find each measure. c. QS 4x - 1 = 3x + 2 QS = 4x - 1 -3x +1 -3x +1 QS = 4(3) - 1 x=3 QS = 12 - 1 Tuesday, February 28, 2012
  • 59.
    Example 3 Find each measure. c. QS 4x - 1 = 3x + 2 QS = 4x - 1 -3x +1 -3x +1 QS = 4(3) - 1 x=3 QS = 12 - 1 QS = 11 Tuesday, February 28, 2012
  • 60.
    Example 4 Find each measure if S is the incenter of ∆MNP. a. SU Tuesday, February 28, 2012
  • 61.
    Example 4 Find each measure if S is the incenter of ∆MNP. a. SU SU is a leg in a right triangle Tuesday, February 28, 2012
  • 62.
    Example 4 Find each measure if S is the incenter of ∆MNP. a. SU SU is a leg in a right triangle a +b =c 2 2 2 Tuesday, February 28, 2012
  • 63.
    Example 4 Find each measure if S is the incenter of ∆MNP. a. SU SU is a leg in a right triangle a +b =c 2 2 2 a + 8 = 10 2 2 2 Tuesday, February 28, 2012
  • 64.
    Example 4 Find each measure if S is the incenter of ∆MNP. a. SU SU is a leg in a right triangle a +b =c 2 2 2 a + 8 = 10 2 2 2 a + 64 = 100 2 Tuesday, February 28, 2012
  • 65.
    Example 4 Find each measure if S is the incenter of ∆MNP. a. SU SU is a leg in a right triangle a +b =c 2 2 2 a + 8 = 10 2 2 2 a + 64 = 100 2 a = 36 2 Tuesday, February 28, 2012
  • 66.
    Example 4 Find each measure if S is the incenter of ∆MNP. a. SU SU is a leg in a right triangle a +b =c 2 2 2 a + 8 = 10 2 2 2 a + 64 = 100 2 a = 36 2 a=6 Tuesday, February 28, 2012
  • 67.
    Example 4 Find each measure if S is the incenter of ∆MNP. a. SU SU is a leg in a right triangle a +b =c 2 2 2 a + 8 = 10 2 2 2 a + 64 = 100 2 a = 36 2 a=6 SU = 6 Tuesday, February 28, 2012
  • 68.
    Example 4 Find each measure if S is the incenter of ∆MNP. b. m∠SPU Tuesday, February 28, 2012
  • 69.
    Example 4 Find each measure if S is the incenter of ∆MNP. b. m∠SPU An incenter is created at the concurrent point of the angle bisectors Tuesday, February 28, 2012
  • 70.
    Example 4 Find each measure if S is the incenter of ∆MNP. b. m∠SPU An incenter is created at the concurrent point of the angle bisectors m∠MNP = 28 + 28 = 56° Tuesday, February 28, 2012
  • 71.
    Example 4 Find each measure if S is the incenter of ∆MNP. b. m∠SPU An incenter is created at the concurrent point of the angle bisectors m∠MNP = 28 + 28 = 56° m∠NMP = 31 + 31 = 62° Tuesday, February 28, 2012
  • 72.
    Example 4 Find each measure if S is the incenter of ∆MNP. b. m∠SPU An incenter is created at the concurrent point of the angle bisectors m∠MNP = 28 + 28 = 56° m∠NMP = 31 + 31 = 62° m∠MPN = 180 − 62 − 56 = 62° Tuesday, February 28, 2012
  • 73.
    Example 4 Find each measure if S is the incenter of ∆MNP. b. m∠SPU An incenter is created at the concurrent point of the angle bisectors m∠MNP = 28 + 28 = 56° m∠NMP = 31 + 31 = 62° m∠MPN = 180 − 62 − 56 = 62° 1 m∠SPU = (62) = 31° 2 Tuesday, February 28, 2012
  • 74.
    Example 4 Find each measure if S is the incenter of ∆MNP. b. m∠SPU An incenter is created at the concurrent point of the angle bisectors m∠MNP = 28 + 28 = 56° m∠NMP = 31 + 31 = 62° m∠MPN = 180 − 62 − 56 = 62° 1 m∠SPU = (62) = 31° 2 Check: 28 + 28 + 31 + 31 + 31 + 31 = 180 Tuesday, February 28, 2012
  • 75.
    Check Your Understading Make sure to review p. 327 #1-8 Tuesday, February 28, 2012
  • 76.
  • 77.
    Problem Set p. 327 #9-29 odd, 48 "Great opportunities to help others seldom come, but small ones surround us every day." - Sally Koch Tuesday, February 28, 2012