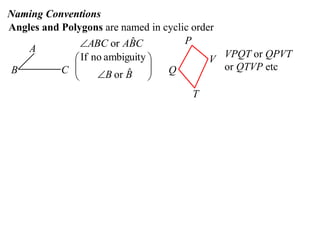
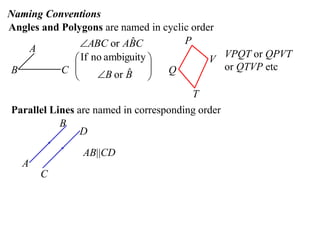
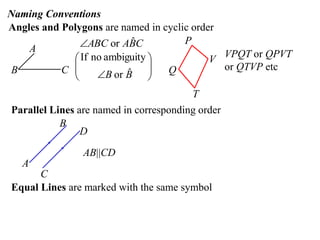
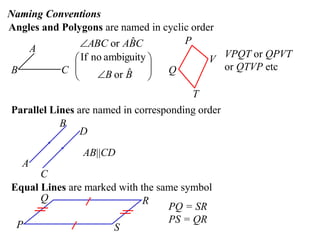
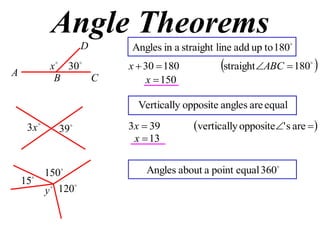
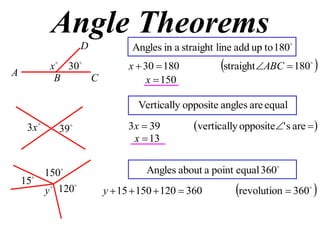
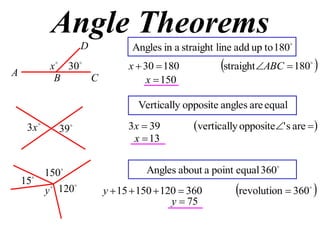
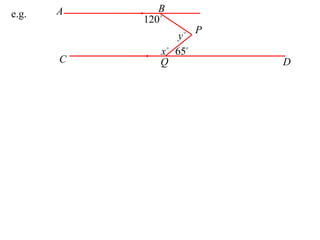
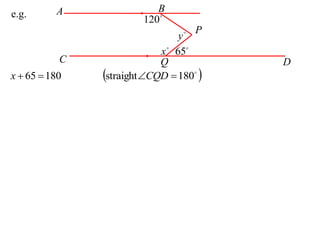
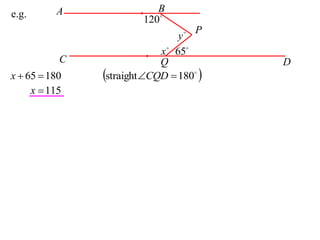
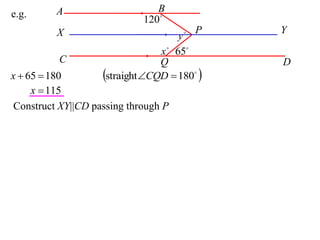
The document defines terminology and notation used in Euclidean geometry. It provides definitions for terms like parallel, perpendicular, congruent, and similar. It also describes conventions for naming angles, polygons, and parallel lines. The document concludes by outlining rules for constructing proofs in geometry, including stating given information, constructions, theorems, and logical reasoning.

1. Euclidean Geometry

2. Euclidean Geometry
Geometry Definitions
Notation
||  is parallel to

3. Euclidean Geometry
Geometry Definitions
Notation
||  is parallel to
  is perpendicular to

4. Euclidean Geometry
Geometry Definitions
Notation
||  is parallel to
  is perpendicular to
  is congruent to

5. Euclidean Geometry
Geometry Definitions
Notation
||  is parallel to
  is perpendicular to
  is congruent to
|||  is similar to

6. Euclidean Geometry
Geometry Definitions
Notation
||  is parallel to
  is perpendicular to
  is congruent to
|||  is similar to
  therefore

7. Euclidean Geometry
Geometry Definitions
Notation
||  is parallel to
  is perpendicular to
  is congruent to
|||  is similar to
  therefore
  because

8. Euclidean Geometry
Geometry Definitions Terminology
Notation produced – the line is extended
||  is parallel to
  is perpendicular to
  is congruent to
|||  is similar to
  therefore
  because

9. Euclidean Geometry
Geometry Definitions Terminology
Notation produced – the line is extended
||  is parallel to
  is perpendicular to X
XY is produced to A
Y A
  is congruent to
|||  is similar to
  therefore
  because

10. Euclidean Geometry
Geometry Definitions Terminology
Notation produced – the line is extended
||  is parallel to
  is perpendicular to B X
XY is produced to A
Y A
  is congruent to
YX is produced to B
|||  is similar to
  therefore
  because

11. Euclidean Geometry
Geometry Definitions Terminology
Notation produced – the line is extended
||  is parallel to
  is perpendicular to B X
XY is produced to A
Y A
  is congruent to
YX is produced to B
|||  is similar to
foot – the base or the bottom
  therefore
  because

12. Euclidean Geometry
Geometry Definitions Terminology
Notation produced – the line is extended
||  is parallel to
  is perpendicular to B X
XY is produced to A
Y A
  is congruent to
YX is produced to B
|||  is similar to
foot – the base or the bottom
  therefore A
B B is the foot of the perpendicular
  because
D C

13. Euclidean Geometry
Geometry Definitions Terminology
Notation produced – the line is extended
||  is parallel to
  is perpendicular to B X
XY is produced to A
Y A
  is congruent to
YX is produced to B
|||  is similar to
foot – the base or the bottom
  therefore A
B B is the foot of the perpendicular
  because
D C
collinear – the points lie on the same line

14. Euclidean Geometry
Geometry Definitions Terminology
Notation produced – the line is extended
||  is parallel to
  is perpendicular to B X
XY is produced to A
Y A
  is congruent to
YX is produced to B
|||  is similar to
foot – the base or the bottom
  therefore A
B B is the foot of the perpendicular
  because
D C
collinear – the points lie on the same line
concurrent – the lines intersect at the same
point

15. Euclidean Geometry
Geometry Definitions Terminology
Notation produced – the line is extended
||  is parallel to
  is perpendicular to B X
XY is produced to A
Y A
  is congruent to
YX is produced to B
|||  is similar to
foot – the base or the bottom
  therefore A
B B is the foot of the perpendicular
  because
D C
collinear – the points lie on the same line
concurrent – the lines intersect at the same
point
transversal – a line that cuts two(or more)
other lines

16. Naming Conventions
Angles and Polygons are named in cyclic order

17. Naming Conventions
Angles and Polygons are named in cyclic order
ABC or ABC ˆ
A
 If no ambiguity 
B C 
 B or B 
ˆ

 

18. Naming Conventions
Angles and Polygons are named in cyclic order
ABC or ABC ˆ P
A
 If no ambiguity  V VPQT or QPVT
B C 
 ˆ
B or B 

 Q or QTVP etc

T

19. Naming Conventions
Angles and Polygons are named in cyclic order
ABC or ABC ˆ P
A
 If no ambiguity  V VPQT or QPVT
B C 
 ˆ
B or B 

 Q or QTVP etc

T
Parallel Lines are named in corresponding order

20. Naming Conventions
Angles and Polygons are named in cyclic order
ABC or ABC ˆ P
A
 If no ambiguity  V VPQT or QPVT
B C 
 ˆ
B or B 

 Q or QTVP etc

T
Parallel Lines are named in corresponding order
B
D
AB||CD
A
C

21. Naming Conventions
Angles and Polygons are named in cyclic order
ABC or ABC ˆ P
A
 If no ambiguity  V VPQT or QPVT
B C 
 ˆ
B or B 

 Q or QTVP etc

T
Parallel Lines are named in corresponding order
B
D
AB||CD
A
C
Equal Lines are marked with the same symbol

22. Naming Conventions
Angles and Polygons are named in cyclic order
ABC or ABC ˆ P
A
 If no ambiguity  V VPQT or QPVT
B C 
 ˆ
B or B 

 Q or QTVP etc

T
Parallel Lines are named in corresponding order
B
D
AB||CD
A
C
Equal Lines are marked with the same symbol
Q R
PQ = SR
P PS = QR
S

23. Constructing Proofs
When constructing a proof, any line that you state must be one of the
following;

24. Constructing Proofs
When constructing a proof, any line that you state must be one of the
following;
1. Given information, do not assume information is given, e.g. if you
are told two sides are of a triangle are equal don’t assume it is
isosceles, state that it is isosceles because two sides are equal.

25. Constructing Proofs
When constructing a proof, any line that you state must be one of the
following;
1. Given information, do not assume information is given, e.g. if you
are told two sides are of a triangle are equal don’t assume it is
isosceles, state that it is isosceles because two sides are equal.
2. Construction of new lines, state clearly your construction so that
anyone reading your proof could recreate the construction.

26. Constructing Proofs
When constructing a proof, any line that you state must be one of the
following;
1. Given information, do not assume information is given, e.g. if you
are told two sides are of a triangle are equal don’t assume it is
isosceles, state that it is isosceles because two sides are equal.
2. Construction of new lines, state clearly your construction so that
anyone reading your proof could recreate the construction.
3. A recognised geometrical theorem (or assumption), any theorem
you are using must be explicitly stated, whether it is in the algebraic
statement or the reason itself.

27. Constructing Proofs
When constructing a proof, any line that you state must be one of the
following;
1. Given information, do not assume information is given, e.g. if you
are told two sides are of a triangle are equal don’t assume it is
isosceles, state that it is isosceles because two sides are equal.
2. Construction of new lines, state clearly your construction so that
anyone reading your proof could recreate the construction.
3. A recognised geometrical theorem (or assumption), any theorem
you are using must be explicitly stated, whether it is in the algebraic
statement or the reason itself.
e.g. A  25  120  180 sum   180

28. Constructing Proofs
When constructing a proof, any line that you state must be one of the
following;
1. Given information, do not assume information is given, e.g. if you
are told two sides are of a triangle are equal don’t assume it is
isosceles, state that it is isosceles because two sides are equal.
2. Construction of new lines, state clearly your construction so that
anyone reading your proof could recreate the construction.
3. A recognised geometrical theorem (or assumption), any theorem
you are using must be explicitly stated, whether it is in the algebraic
statement or the reason itself.
e.g. A  25  120  180 sum   180
Your reasoning should be clear and concise

29. Constructing Proofs
When constructing a proof, any line that you state must be one of the
following;
1. Given information, do not assume information is given, e.g. if you
are told two sides are of a triangle are equal don’t assume it is
isosceles, state that it is isosceles because two sides are equal.
2. Construction of new lines, state clearly your construction so that
anyone reading your proof could recreate the construction.
3. A recognised geometrical theorem (or assumption), any theorem
you are using must be explicitly stated, whether it is in the algebraic
statement or the reason itself.
e.g. A  25  120  180 sum   180
Your reasoning should be clear and concise
4. Any working out that follows from lines already stated.

30. Angle Theorems

31. Angle Theorems
Angles in a straight line add up to 180

32. Angle Theorems
D Angles in a straight line add up to 180
x  30
A B C

33. Angle Theorems
D Angles in a straight line add up to 180
A
x  30 x  30  180 straight ABC  180 

B C

34. Angle Theorems
D Angles in a straight line add up to 180
A
x  30 x  30  180 straight ABC  180 

B C x  150

35. Angle Theorems
D Angles in a straight line add up to 180
A
x  30 x  30  180 straight ABC  180 

B C x  150
Vertically opposite angles are equal

36. Angle Theorems
D Angles in a straight line add up to 180
A
x  30 x  30  180 straight ABC  180 

B C x  150
Vertically opposite angles are equal
3x  39

37. Angle Theorems
D Angles in a straight line add up to 180
A
x  30 x  30  180 straight ABC  180 
B C x  150
Vertically opposite angles are equal
3x  39 3x  39 vertically opposite' s are 

38. Angle Theorems
D Angles in a straight line add up to 180
A
x  30 x  30  180 straight ABC  180 
B C x  150
Vertically opposite angles are equal
3x  39 3x  39 vertically opposite' s are 
x  13

39. Angle Theorems
D Angles in a straight line add up to 180
A
x  30 x  30  180 straight ABC  180 
B C x  150
Vertically opposite angles are equal
3x  39 3x  39 vertically opposite' s are 
x  13
Angles about a point equal 360

40. Angle Theorems
D Angles in a straight line add up to 180
A
x  30 x  30  180 straight ABC  180 
B C x  150
Vertically opposite angles are equal
3x  39 3x  39 vertically opposite' s are 
x  13
150  Angles about a point equal 360

15
y120

41. Angle Theorems
D Angles in a straight line add up to 180
A
x  30 x  30  180 straight ABC  180 
B C x  150
Vertically opposite angles are equal
3x  39 3x  39 vertically opposite' s are 
x  13
150  Angles about a point equal 360

15
y120 y  15  150  120  360 revolution  360 


42. Angle Theorems
D Angles in a straight line add up to 180
A
x  30 x  30  180 straight ABC  180 
B C x  150
Vertically opposite angles are equal
3x  39 3x  39 vertically opposite' s are 
x  13
150  Angles about a point equal 360

15
y120 y  15  150  120  360 revolution  360 

y  75

43. Parallel Line Theorems
a bd
c f
e h
g

44. Parallel Line Theorems
Alternate angles (Z) are equal a bd
c f
e h
g

45. Parallel Line Theorems
Alternate angles (Z) are equal a bd
c f
c f alternate' s , || lines  e h
g

46. Parallel Line Theorems
Alternate angles (Z) are equal a bd
c f
c f alternate' s , || lines  e h
d e g

47. Parallel Line Theorems
Alternate angles (Z) are equal a bd
c f
c f alternate' s , || lines  e h
d e g
Corresponding angles (F) are equal

48. Parallel Line Theorems
Alternate angles (Z) are equal a bd
c f
c f alternate' s , || lines  e h
d e g
Corresponding angles (F) are equal
ae corresponding' s , || lines 

49. Parallel Line Theorems
Alternate angles (Z) are equal a bd
c f
c f alternate' s , || lines  e h
d e g
Corresponding angles (F) are equal
ae corresponding' s , || lines 
b f
cg
d h

50. Parallel Line Theorems
Alternate angles (Z) are equal a bd
c f
c f alternate' s , || lines  e h
d e g
Corresponding angles (F) are equal
ae corresponding' s , || lines 
b f
cg
d h
Cointerior angles (C) are supplementary

51. Parallel Line Theorems
Alternate angles (Z) are equal a bd
c f
c f alternate' s , || lines  e h
d e g
Corresponding angles (F) are equal
ae corresponding' s , || lines 
b f
cg
d h
Cointerior angles (C) are supplementary
c  e  180 cointerior' s  180, || lines 

52. Parallel Line Theorems
Alternate angles (Z) are equal a bd
c f
c f alternate' s , || lines  e h
d e g
Corresponding angles (F) are equal
ae corresponding' s , || lines 
b f
cg
d h
Cointerior angles (C) are supplementary
c  e  180 cointerior' s  180, || lines 
d  f  180

53. A B
e.g.
120
 P
y
x  65
C Q D

54. A B
e.g.
120
 P
y
x  65
C Q D
x  65  180 straight CQD  180 

55. A B
e.g.
120
 P
y
x  65
C Q D
x  65  180 straight CQD  180 
x  115

56. A B
e.g.
120
X  P Y
y
x  65
C Q D
x  65  180 straight CQD  180 
x  115
Construct XY||CD passing through P

57. A B
e.g.
120
X  P Y
y
x  65
C Q D
x  65  180 straight CQD  180 
x  115
Construct XY||CD passing through P
XPQ  65 alternate' s , XY || CQ 

58. A B
e.g.
120
X  P Y
y
x  65
C Q D
x  65  180 straight CQD  180 
x  115
Construct XY||CD passing through P
XPQ  65 alternate' s , XY || CQ 
XPB  120  180 cointerior' s  180 , AB || XY 


59. A B
e.g.
120
X  P Y
y
x  65
C Q D
x  65  180 straight CQD  180 
x  115
Construct XY||CD passing through P
XPQ  65 alternate' s , XY || CQ 
XPB  120  180 cointerior' s  180 , AB || XY 

XPB  60

60. A B
e.g.
120
X  P Y
y
x  65
C Q D
x  65  180 straight CQD  180 
x  115
Construct XY||CD passing through P
XPQ  65 alternate' s , XY || CQ 
XPB  120  180 cointerior' s  180 , AB || XY 

XPB  60
BPQ  XPQ  XPB common 

61. A B
e.g.
120
X  P Y
y
x  65
C Q D
x  65  180 straight CQD  180 
x  115
Construct XY||CD passing through P
XPQ  65 alternate' s , XY || CQ 
XPB  120  180 cointerior' s  180 , AB || XY 

XPB  60
BPQ  XPQ  XPB common 
y  65  60
y  125

62. A B
e.g.
120
X  P Y
y
x  65
C Q D
x  65  180 straight CQD  180 
x  115
Construct XY||CD passing through P
Book 2
XPQ  65 alternate' s , XY || CQ  Exercise 8A;
XPB  120  180 cointerior' s  180 , AB || XY 

1cfh, 2bdeh,
3bd, 5bcf,
XPB  60
6bef, 10bd,
BPQ  XPQ  XPB common  11b, 12bc,
y  65  60 13ad, 14, 15
y  125