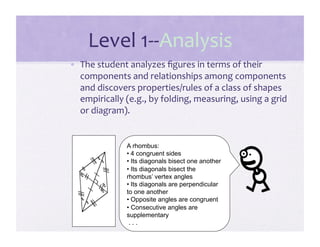
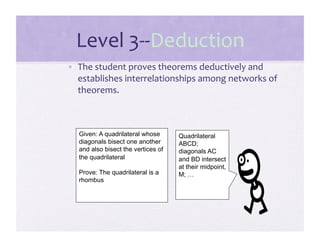
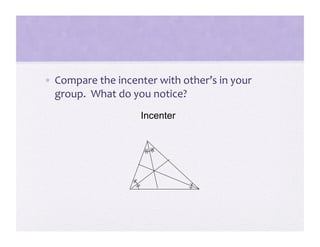
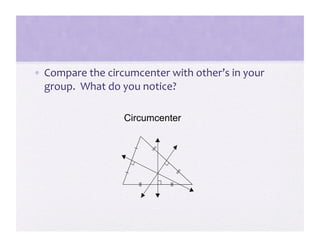
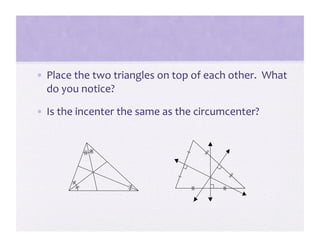
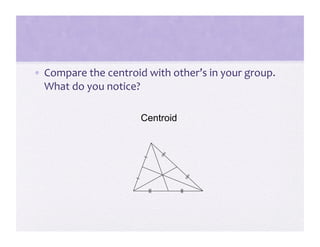
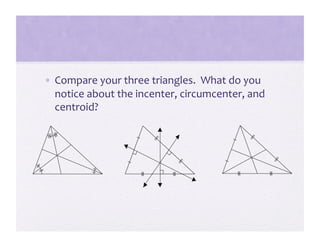
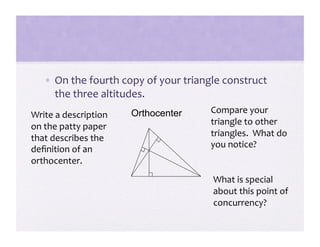
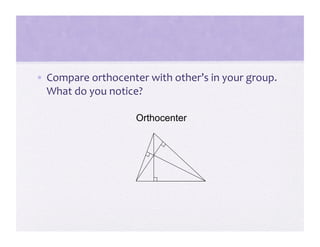
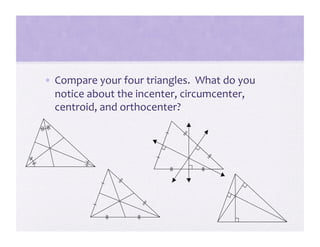
1) The document discusses van Hiele levels of geometric reasoning, which describe how students develop understanding of geometry concepts through sequential levels of learning. 2) It provides details on the five van Hiele levels - visualization, analysis, abstraction, deduction, and rigor - and examples of the types of thinking associated with each level. 3) Activities are presented that involve organizing shapes, constructing geometric figures without tools, and investigating properties of triangles to help students advance through the van Hiele levels.

1. Geometry
MELL 2010
July 08, 2010
Texas State University, San Marcos
Dr. Beth Bos

2. Activity #1
Cut out all the shapes on handout #1 and
organize them in a way that makes sense to
you. Then be prepared to describe your
method for organizing the shapes.

3. van Hiele Levels
• Developed by Pierre M. van Hiele and his wife
Dina van Hiele‐Geldof

4. • The Van Hiele levels of geometric reasoning are
sequential. Students must pass through all prior levels to
arrive at any specific level.
• These levels are not age‐dependent in the way Piaget
described development.
• Geometric experiences have the greatest influence on
advancement through the levels.
• Instruction and language at a level higher than the level
of the student may inhibit learning.
John A. Van de Walle, Elementary and Middle School Mathematics: Teaching
Developmentally, 4th ed. (New York: Addison Wesley Longman, 2001), pp. 310‐11.

5. Level 0‐‐Basic
Visualization
• The student identifies, names, compares and
operates on geometric figures (e.g., triangles,
angles, intersecting or parallel lines) according to
their appearance as a whole.

6. Level 1‐‐Analysis
• The student analyzes figures in terms of their
components and relationships among components
and discovers properties/rules of a class of shapes
empirically (e.g., by folding, measuring, using a grid
or diagram).
A rhombus:
• 4 congruent sides
• Its diagonals bisect one another
• Its diagonals bisect the
rhombus’ vertex angles
• Its diagonals are perpendicular
to one another
• Opposite angles are congruent
• Consecutive angles are
supplementary
...

7. Level 2‐‐Informal
Deduction
• The student logically interrelates previously
discovered properties/rules by giving or following
informal arguments.
A quadrilateral
in which It’s a
rhombus
diagonals bisect
!
one another
and the vertex
angles

8. Level 3‐‐Deduction
• The student proves theorems deductively and
establishes interrelationships among networks of
theorems.
Given: A quadrilateral whose Quadrilateral
diagonals bisect one another ABCD;
and also bisect the vertices of diagonals AC
the quadrilateral and BD intersect
at their midpoint,
Prove: The quadrilateral is a M; …
rhombus

9. Level 4‐‐Rigor
• The student establishes theorems in
different postulational systems and
analyzes/compares these systems.
Well, if we consider the
implications of this
figure drawn in a non-
Euclidean plane . . .

10. What shape is this?

11. Match the response to the van Hiele level
• It is a rectangle because it is a quadrilateral with
four right angles, the opposites are parallel, and
consecutive sides are perpendicular.
• I can prove it’s a rectangle if it’s a parallelogram
with one right angle.
• I know it’s a rectangle if it’s a quadrilateral with four
right angles.
• It is a rectangle because it looks like a door.
• Well, if I draw that rectangle on a sphere . . .

12. • Recent research on how students learn
mathematics indicates students should
• Be doing hands-on activities with
emphasis on exploring relationships and
seeing patterns rather than on calculating
answers
• Working in cooperative groups settings
• to learn to communicate about mathematics,
• to see various approaches to problems and
• to learn to support each other in a learning
atmosphere
• Be engaged in problem-solving lessons
• Be asked to justify their answers
• Engage with constructive assessments.

14. Find
1. equilateral 7. trapezoid (non-
triangle isosceles)
2. isosceles triangle 8. isosceles trapezoid
(non-equilateral) 9. pentagon
3. right triangle 10.hexagon
4. scalene triangle 11.heptagon
5. parallelogram 12.octagon
(not a rectangle or
rhombus)
6. rectangle

15. círculo circle The set of all points in a plane a given distance
from a given point
congruente congruent Equal measure
hexágono hexagon A six-sided polygon
heptágono heptagon A seven-sided polygon
octágono octagon An eight-sided polygon
Paralelogramo parallelogra A quadrilateral with both pairs of opposite sides
m parallel
pentágono pentagon A five-sided polygon
semejante similar Figures that have the same shape, but not
necessarily the same size
rectángulo rectangle A quadrilateral with 4 right angles
trapezoide trapezoid A quadrilateral with exactly one pair of opposite
sides parallel
isósceles isosceles A trapezoid with n-parallel opposite sides
congruent
triángulo triangle A 3-sided polygon
equilátero equilateral A triangle with all sides congruent
recto right A triangle with a right angle
escaleno scalene A triangle with no sides congruent

16. Investigating with
Patty Paper

17. Patty Paper
Constructions

18. Patty Paper
Constructions
• Draw a line segment on one sheet of
patty paper. Discover a way to make a
duplicate segment without using the
marks on a ruler. Describe your
method.
• Draw any angle on one sheet of patty
paper. Discover a way to make a
duplicate angle without using a
protractor. Describe your method.

19. Patty Paper
Constructions
• Use one your angles from the last activity.
Discover a way to create an angle bisector of
the angle.
• Describe your method.
• How do you know you have an angle bisector?

20. Patty Paper
Constructions
• Draw a line segment on a sheet of patty paper.
Discover a way to create a perpendicular
bisector of the line segment without using a
protractor or ruler.
• Describe your method.
• How do you know you have created a
perpendicular bisector?

21. Patty Paper
Constructions
• Draw a line on a sheet of patty paper. Select
and label any point on the line. Discover a way
to create a perpendicular to the line through
the indicated point.
• Describe your method.
• How do you know you have created a
perpendicular line?

22. Patty Paper
Constructions
• Draw a line on a sheet of patty paper. Select
and label a point off the line. Discover a way to
create a perpendicular through the indicated
points that is perpendicular to the line.
• Describe your method.
• How do you know your line is perpendicular to
the original line?

23. An Investigation with
Patty Paper
• On a sheet of patty paper draw a line segment. Label
the two endpoints A and B. Construct the perpendicular
bisector of the segment.
• Select several points on the perpendicular
bisector and label them.
• Using a ruler compare the distance between
each of these points and the two endpoints.
Label these measurements on the patty paper.
Describe what you find to be true.
• Compare your results with others around you.
What conclusion can you make about every
point that is equidistant (the same distance)
from the endpoints of a line segment?

24. Think about this statement
If is a line segment, then C
is a midpoint if AC = BC.
• When is this statement
true?
• When is this statement
false?

25. Creating Points of
Concurrency

26. • Work in groups:
• Each person will draw a different triangle
• scalene acute triangle
• scalene obtuse triangle
• scalene right triangle
• Make three copies of your triangle

27. • On one of the triangles fold (or construct) the
three angle bisectors.
Write a description Incenter Compare your
on the patty paper triangle to other
that describes the triangles. What do
definition of an you notice?
incenter.
What is special
about this point of
concurrency?

28. • Compare the incenter with other’s in your
group. What do you notice?
Incenter

29. • On the second copy of the triangle fold the
three perpendicular bisectors of the sides
Circumcenter Compare your
Write a description
triangle to other
on the patty paper
triangles. What do
that describes the
you notice?
definition of an
circumcenter.
What is special
about this point of
concurrency?

30. • Compare the circumcenter with other’s in your
group. What do you notice?
Circumcenter

31. • Place the two triangles on top of each other. What
do you notice?
• Is the incenter the same as the circumcenter?

32. • On a third copy of your triangle construct
the three medians.
Centroid Compare your
Write a description
triangle to other
on the patty paper
that describes the triangles. What do
you notice?
definition of an
centroid.
What is special
about this point of
concurrency?

33. • Compare the centroid with other’s in your group.
What do you notice?
Centroid

34. • Compare your three triangles. What do you
notice about the incenter, circumcenter, and
centroid?

35. • On the fourth copy of your triangle construct
the three altitudes.
Orthocenter Compare your
Write a description
triangle to other
on the patty paper
that describes the triangles. What do
you notice?
definition of an
orthocenter.
What is special
about this point of
concurrency?

36. • Compare orthocenter with other’s in your group.
What do you notice?
Orthocenter

37. • Compare your four triangles. What do you
notice about the incenter, circumcenter,
centroid, and orthocenter?

38. GeoGebra
• www. geogebra.org/en/wiki/index.php/English

39. Sketchup
• http://sketchup.google.com