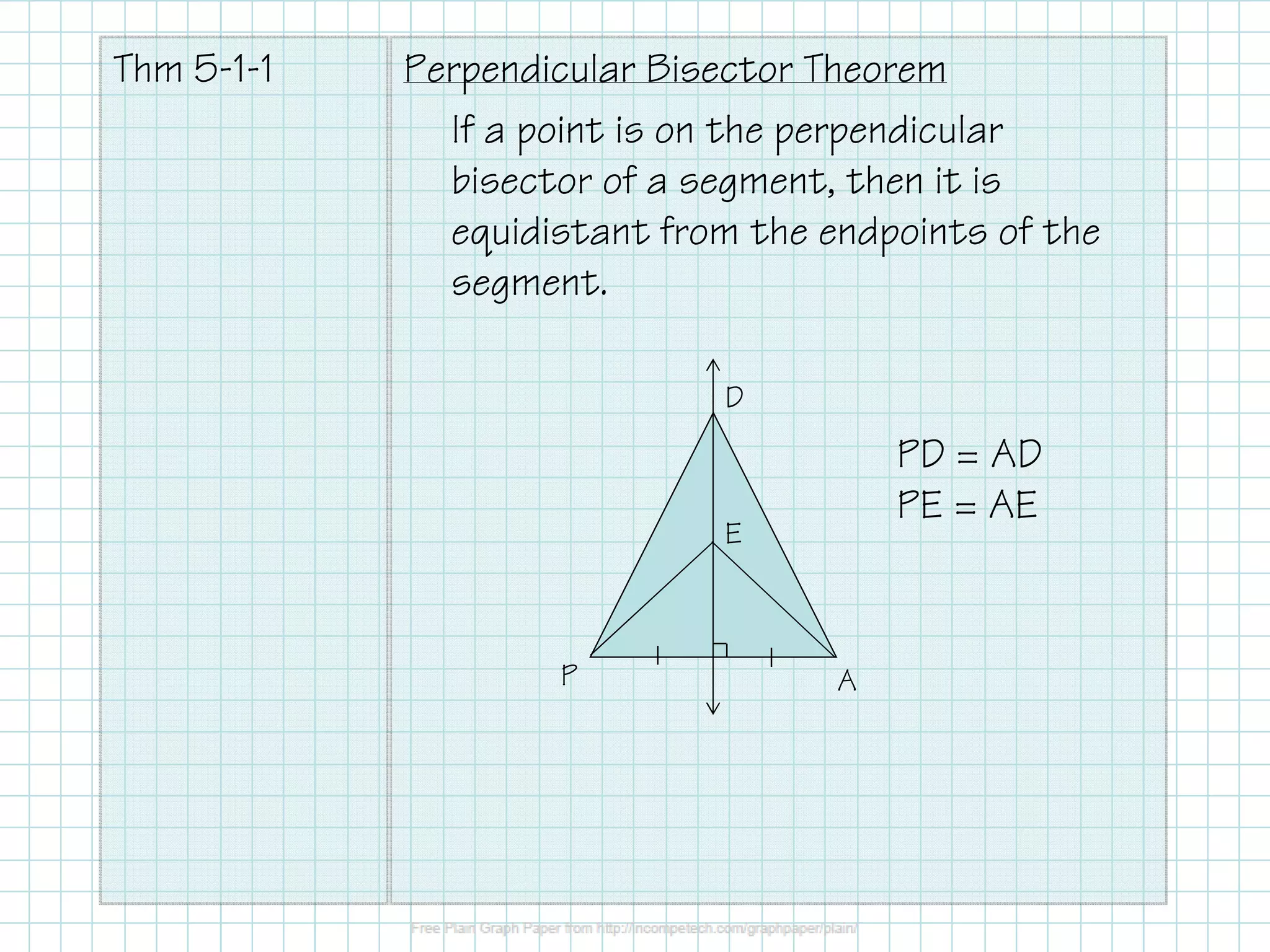
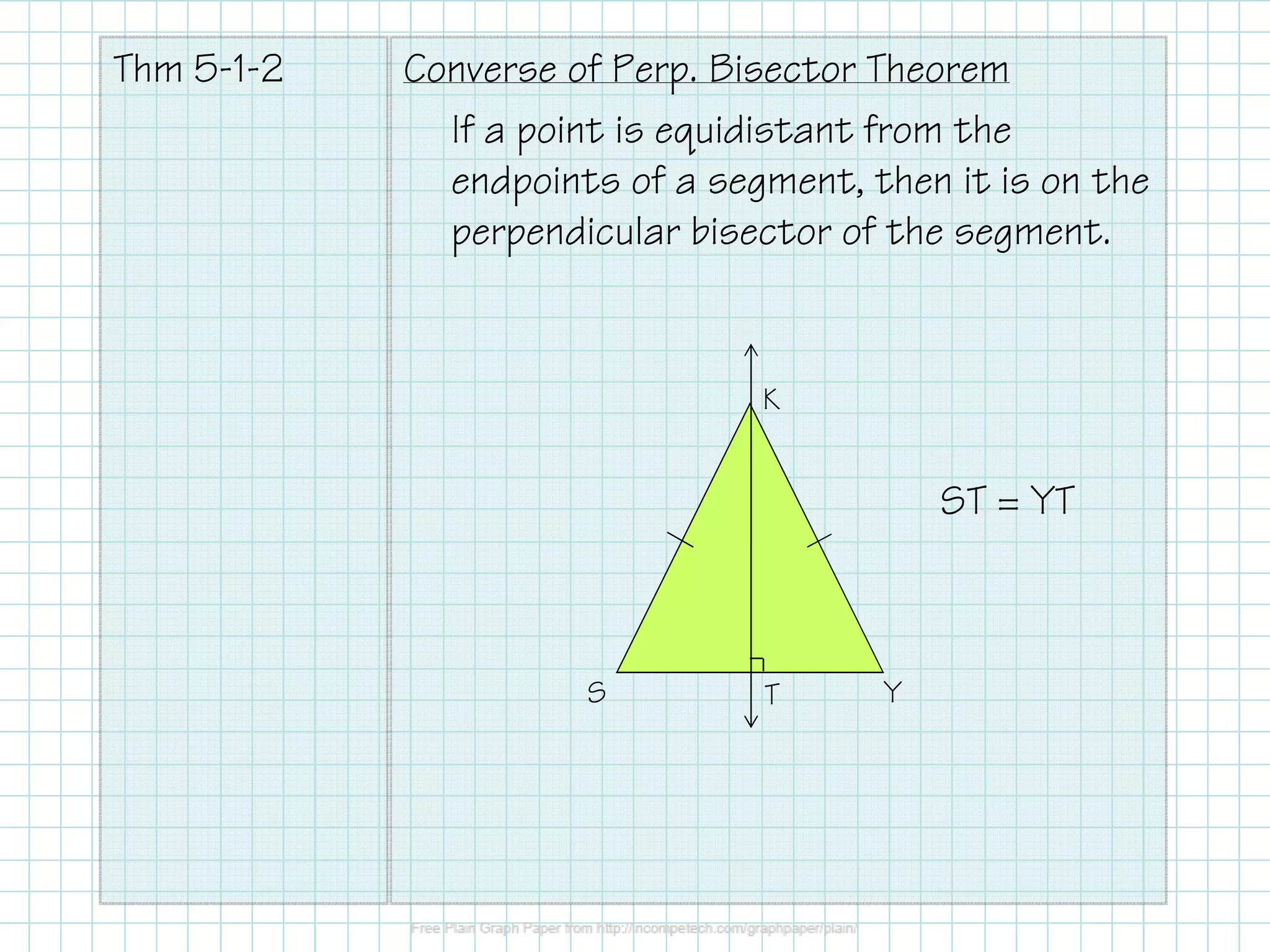
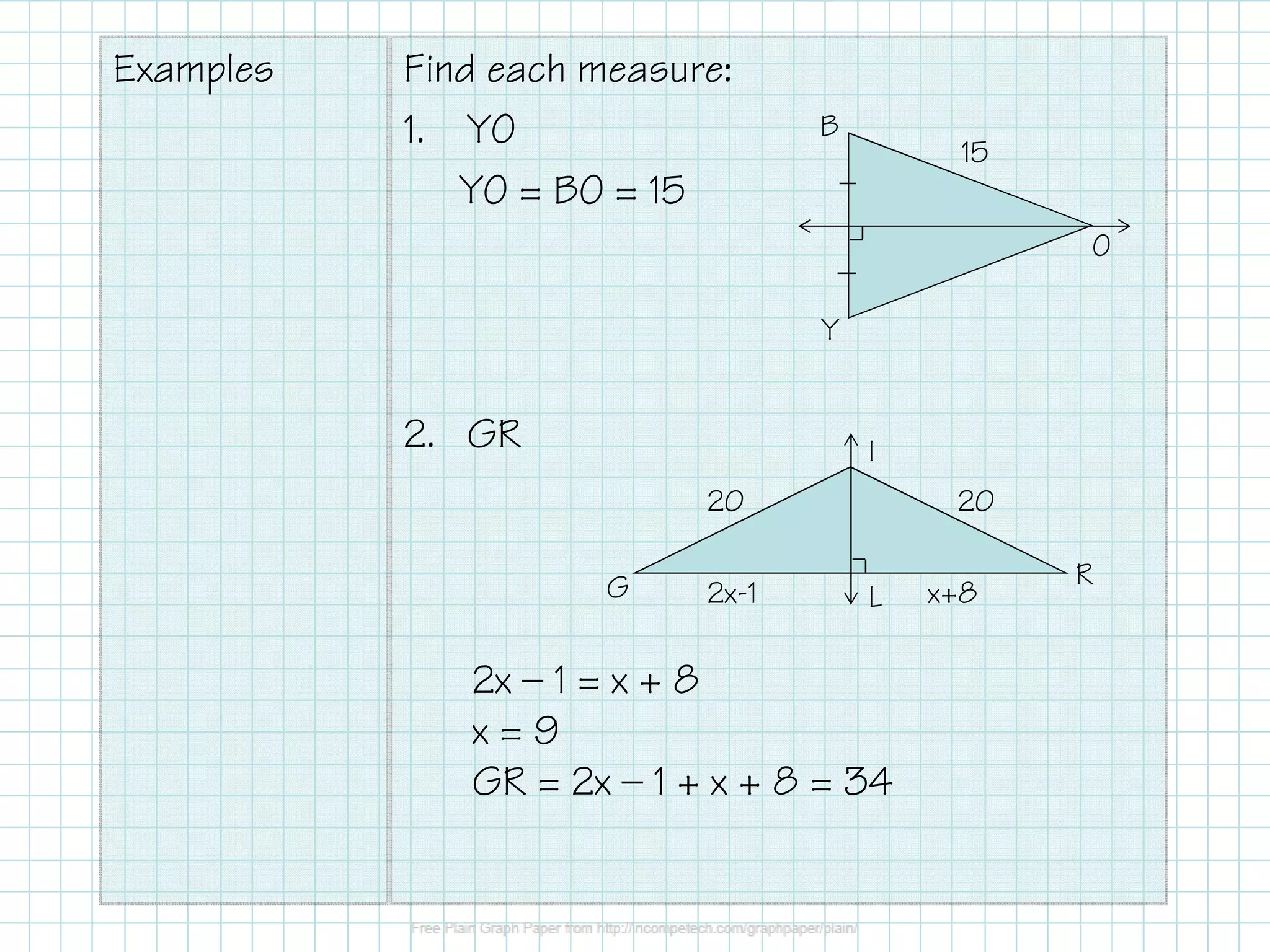
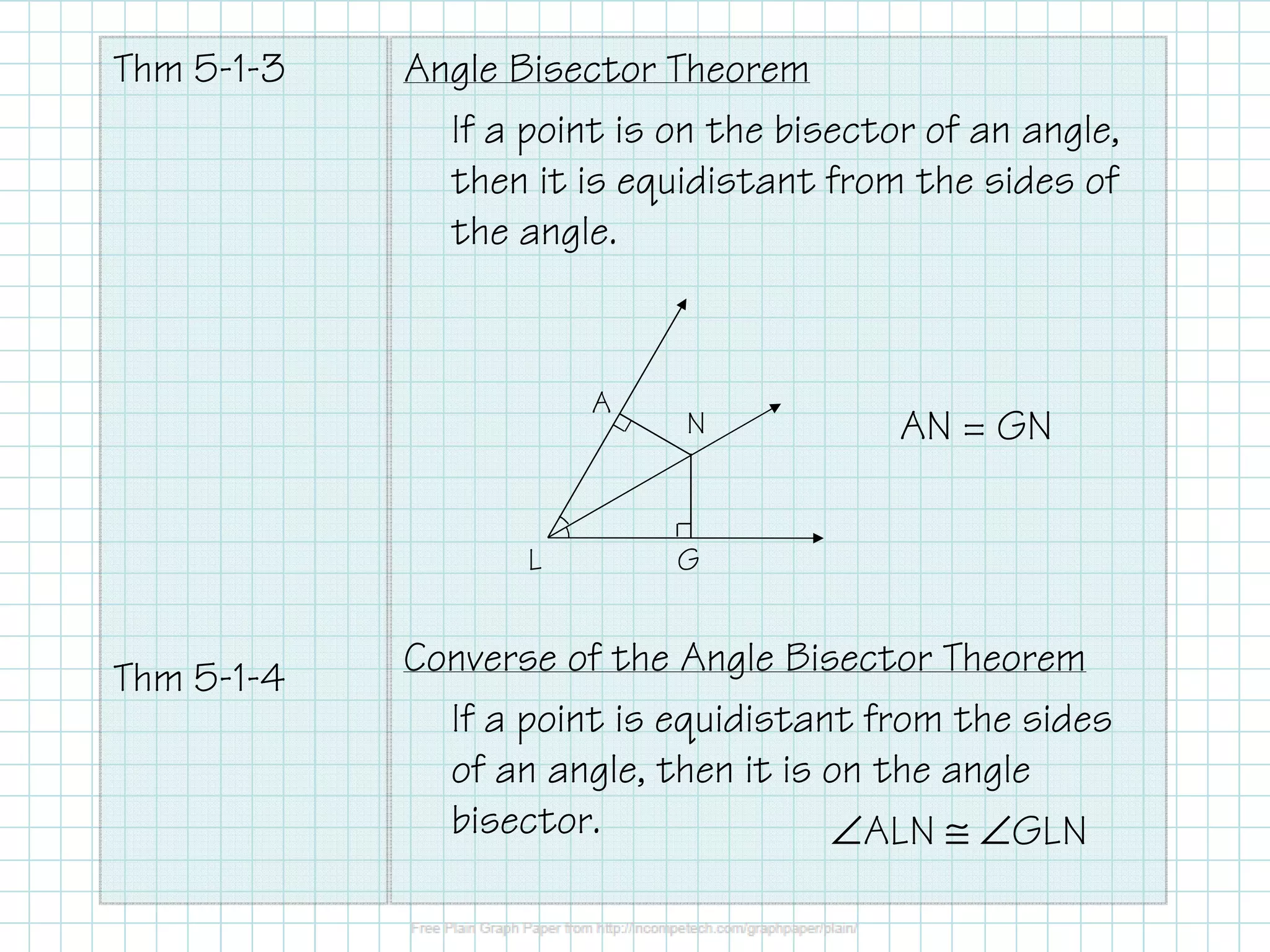
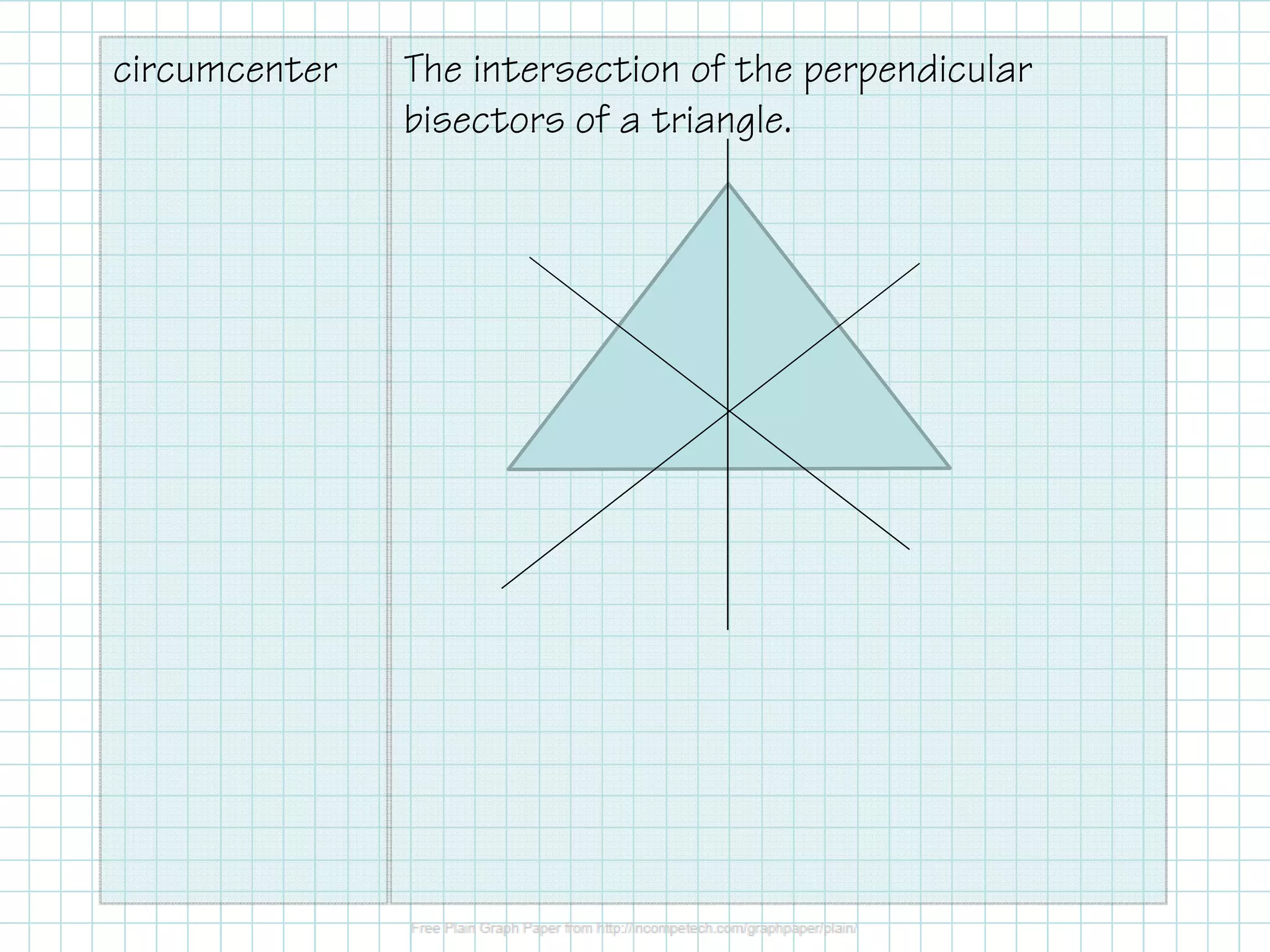
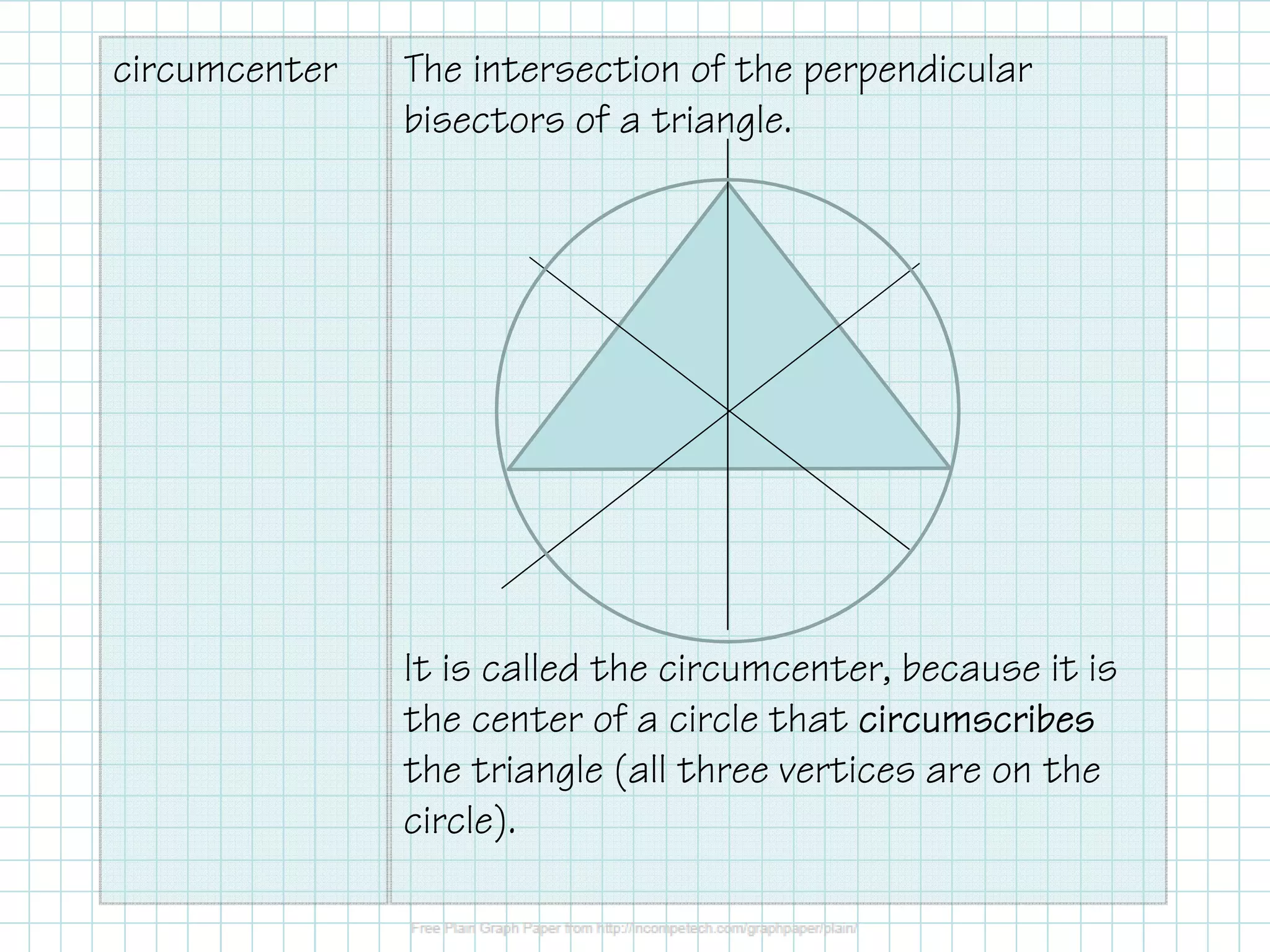
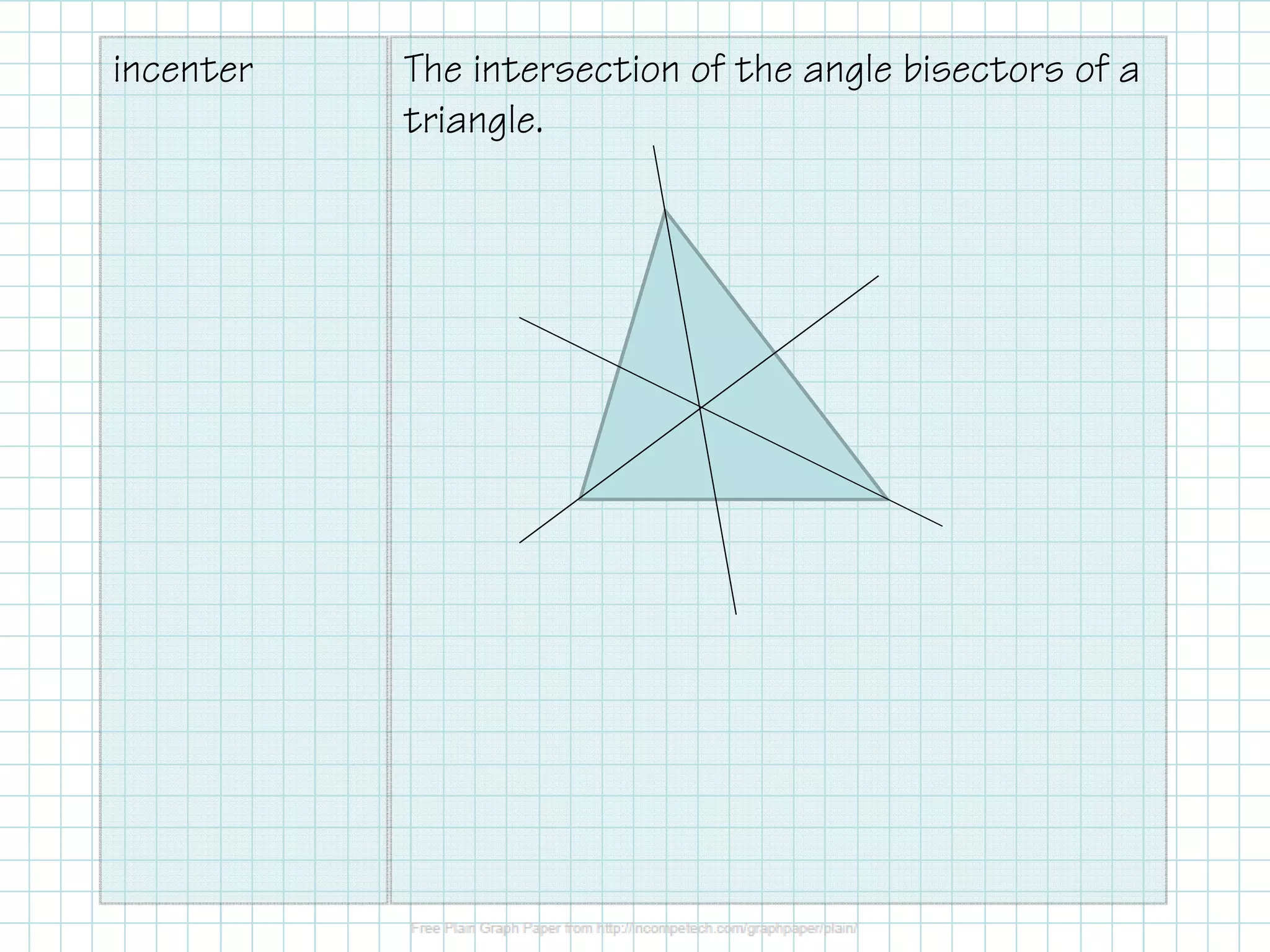
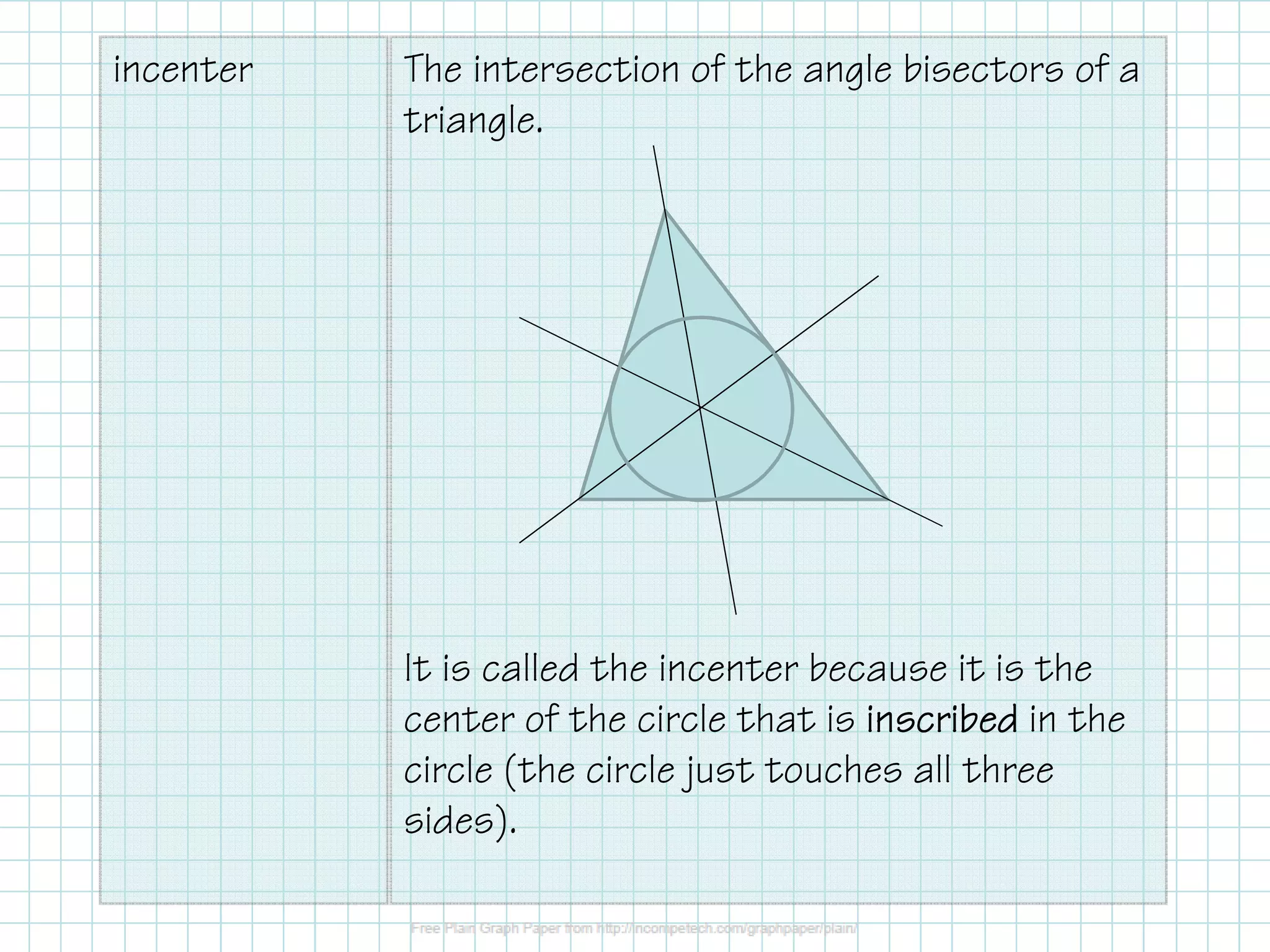
The document covers the construction of perpendicular and angle bisectors, their applications, and properties related to triangles, such as the circumcenter and incenter. It includes theorems regarding the equidistance of points to segment endpoints and angle sides when on a bisector. Examples are provided to illustrate these concepts and calculations.

1. Obj. 20 Bisectors
The student is able to (I can):
• Construct perpendicular and angle bisectors
• Use bisectors to solve problems
• Identify the circumcenter and incenter of a triangle

2. Thm 5-1-1 Perpendicular Bisector Theorem
If a point is on the perpendicular
bisector of a segment, then it is
equidistant from the endpoints of the
segment.
P
D
A
E
PD = AD
PE = AE

3. Thm 5-1-2 Converse of Perp. Bisector Theorem
If a point is equidistant from the
endpoints of a segment, then it is on the
perpendicular bisector of the segment.
S
K
T Y
ST = YT

4. Examples Find each measure:
1. YO
YO = BO = 15
2. GR
B
O
Y
15
G
I
R
20 20
2x-1 x+8
L
2x — 1 = x + 8
x = 9
GR = 2x — 1 + x + 8 = 34

5. Thm 5-1-3
Thm 5-1-4
Angle Bisector Theorem
If a point is on the bisector of an angle,
then it is equidistant from the sides of
the angle.
A
N AN = GN
L G
Converse of the Angle Bisector Theorem
If a point is equidistant from the sides
of an angle, then it is on the angle
bisector.
ÐALN @ ÐGLN

6. circumcenter The intersection of the perpendicular
bisectors of a triangle.

7. circumcenter The intersection of the perpendicular
bisectors of a triangle.
It is called the circumcenter, because it is
the center of a circle that cccciiiirrrrccccuuuummmmssssccccrrrriiiibbbbeeeessss
the triangle (all three vertices are on the
circle).

8. incenter The intersection of the angle bisectors of a
triangle.

9. incenter The intersection of the angle bisectors of a
triangle.
It is called the incenter because it is the
center of the circle that is iiiinnnnssssccccrrrriiiibbbbeeeedddd in the
circle (the circle just touches all three
sides).