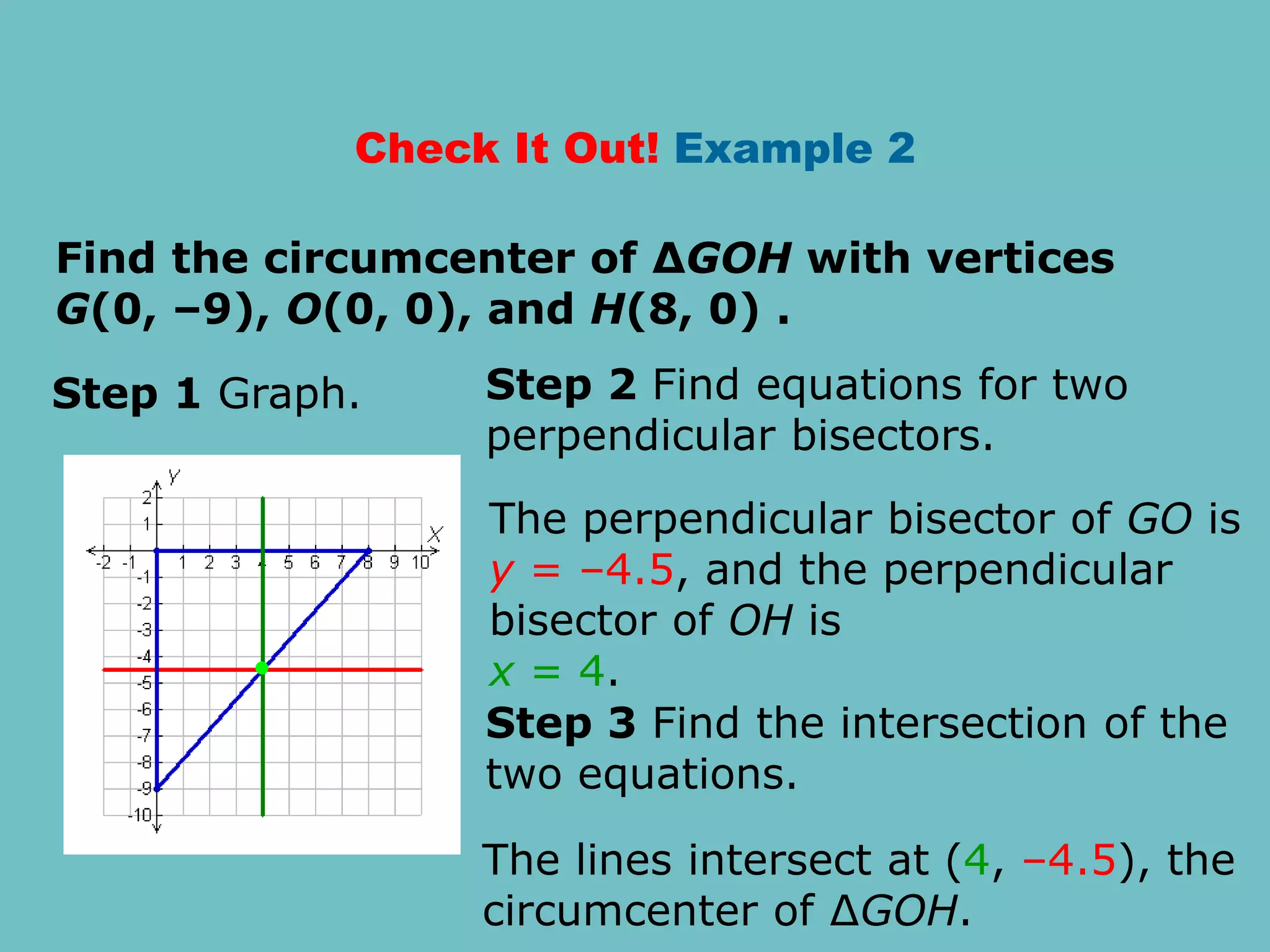
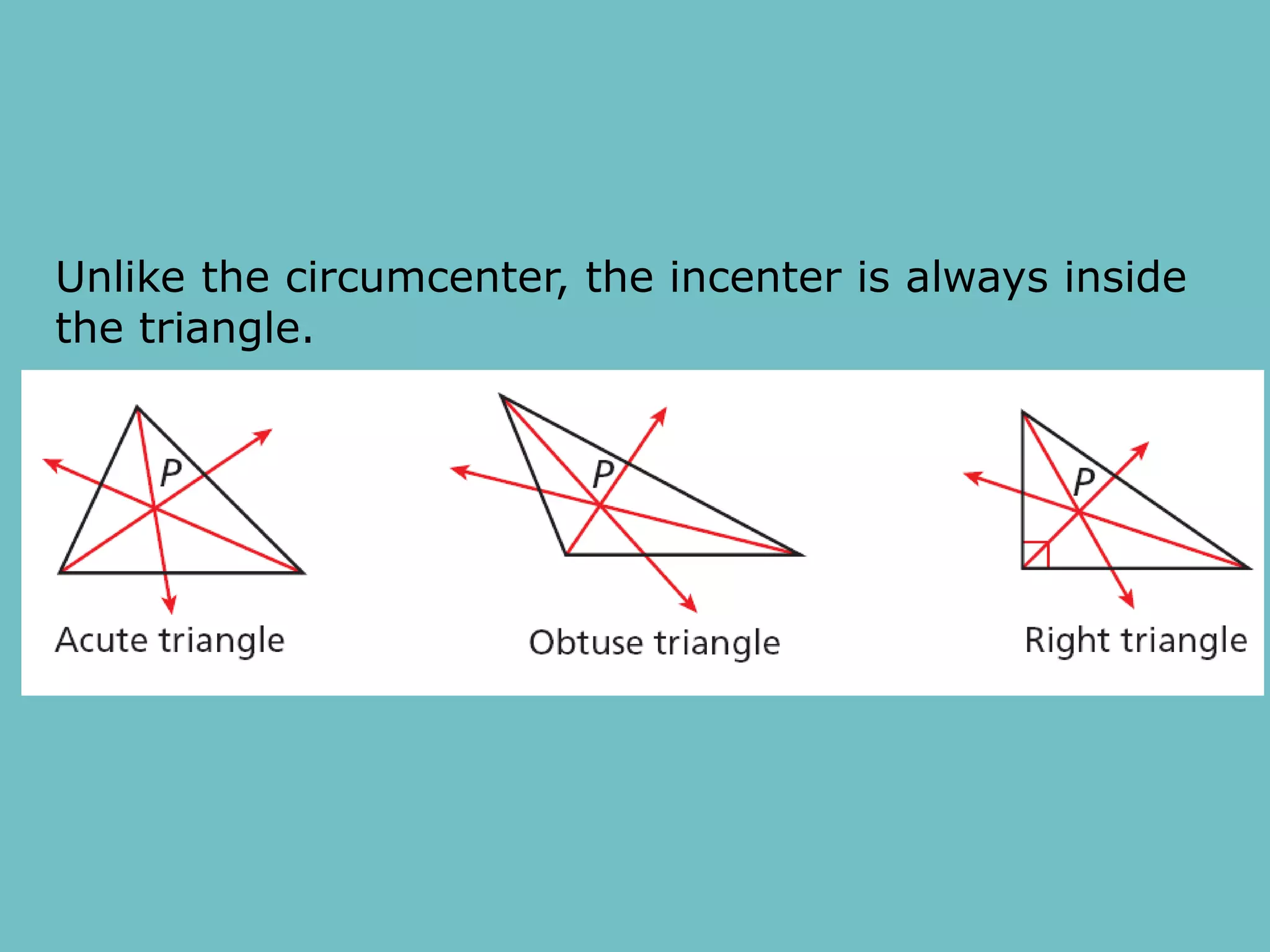
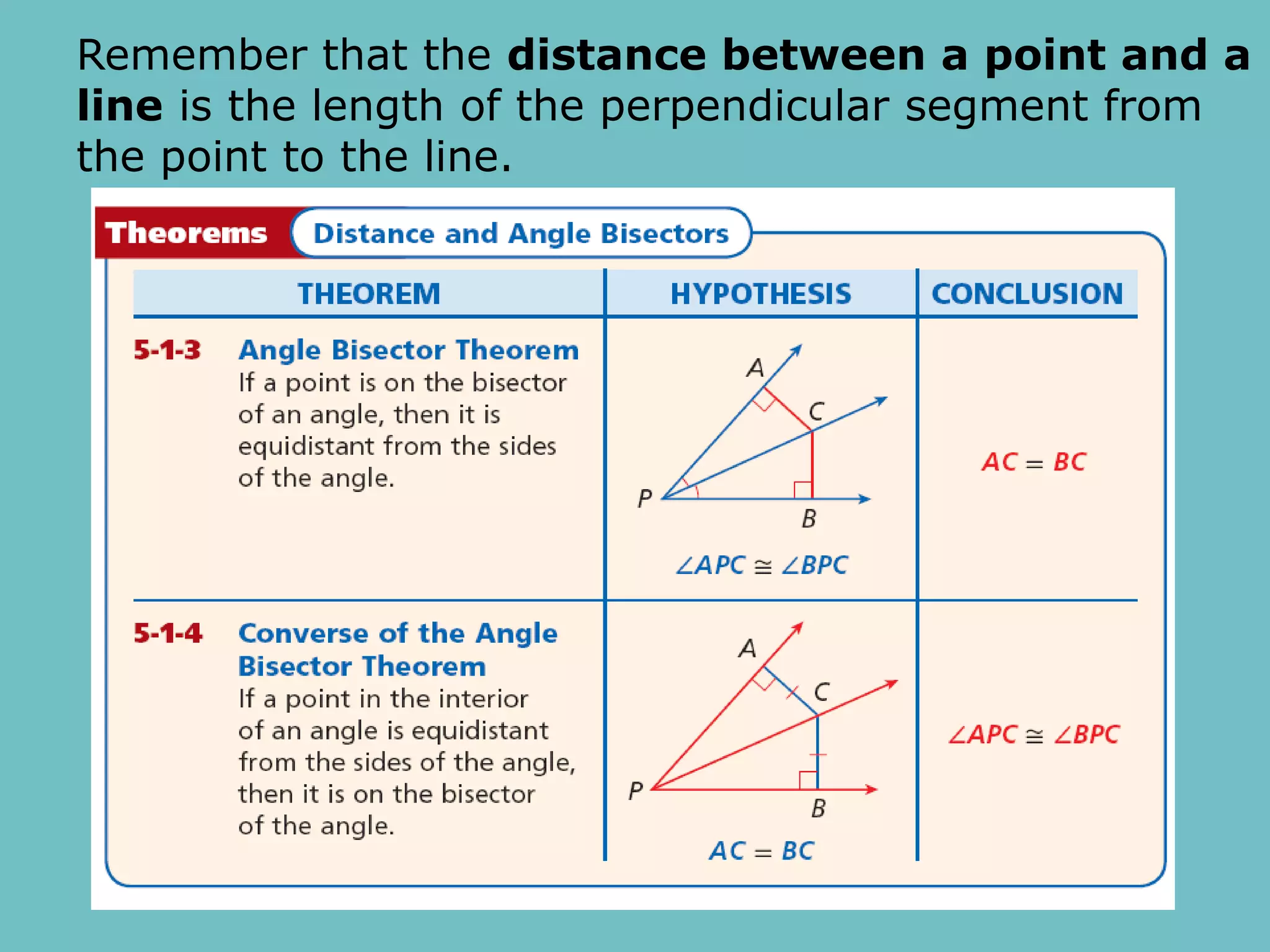
This document discusses theorems and properties related to perpendicular bisectors, angle bisectors, and the circumcenter and incenter of triangles. It provides examples of applying theorems about perpendicular bisectors to find missing lengths and applying properties of angle bisectors to find missing measures of angles. The document also defines key terms like locus, equidistant, concurrent, circumscribed circle, and inscribed circle as they relate to bisectors and triangle centers.

1. Prove and apply theorems about
perpendicular bisectors.
Prove and apply theorems about angle
bisectors.

2. A locus is a set of points that satisfies a given
condition. The perpendicular bisector of a segment
can be defined as the locus of points in a plane that
are equidistant from the endpoints of the segment.
When a point is the same distance from two or more
objects, the point is said to be equidistant from
the objects. Triangle congruence theorems can be
used to prove theorems about equidistant points.

4. Example 1A: Applying the Perpendicular Bisector
Theorem and Its Converse
Find each measure.
MN
MN = LN
MN = 2.6
 Bisector Thm.
Substitution

5. Example 1C: Applying the Perpendicular Bisector
Theorem and Its Converse
TU
Find each measure.
So TU = 3(6.5) + 9 = 28.5.
TU = UV  Bisector Thm.
3x + 9 = 7x – 17
9 = 4x – 17
26 = 4x
6.5 = x
Subtraction POE
Addition POE.
Division POE.
Substitution

6. Check It Out! Example 1b
Given that DE = 20.8, DG = 36.4,
and EG =36.4, which Theorem
would you use to find EF?
Find the measure.
Since DG = EG and , is the
perpendicular bisector of by
the Converse of the Perpendicular
Bisector Theorem.

8. Remember that the distance between a point and a
line is the length of the perpendicular segment from
the point to the line.

9. Example 2A: Applying the Angle Bisector Theorem
Find the measure. BC
BC = DC
BC = 7.2
 Bisector Thm.
Substitution
Find the measure.
mEFH, given that mEFG = 50°.
Since EH = GH,
and , bisects
EFG by the Converse
of the Angle Bisector Theorem.

10. Example 2C: Applying the Angle Bisector Theorem
Find mMKL.
, bisects JKL
Since, JM = LM, and
by the Converse of the Angle
Bisector Theorem.
mMKL = mJKM
3a + 20 = 2a + 26
a + 20 = 26
a = 6
Def. of  bisector
Substitution.
Subtraction POE
Subtraction POE
So mMKL = [2(6) + 26]° = 38°

11. Check It Out! Example 2a
Given that mWYZ = 63°, XW = 5.7,
and ZW = 5.7, find mXYZ.
mWYZ = mWYX
mWYZ + mWYX = mXYZ
mWYZ + mWYZ = mXYZ
2(63°) = mXYZ
126° = mXYZ
2mWYZ = mXYZ

12. Prove and apply properties of
perpendicular bisectors of a triangle.
Prove and apply properties of angle
bisectors of a triangle.

13. The perpendicular bisector of a side of a triangle
does not always pass through the opposite
vertex.
Helpful Hint

14. When three or more lines intersect at one point, the
lines are said to be concurrent. The point of
concurrency is the point where they intersect. In the
construction, you saw that the three perpendicular
bisectors of a triangle are concurrent. This point of
concurrency is the circumcenter of the triangle.

15. The circumcenter can be inside the triangle, outside
the triangle, or on the triangle.

16. The circumcenter of ΔABC is the center of its
circumscribed circle. A circle that contains all the
vertices of a polygon is circumscribed about the
polygon.

17. Example 1: Using Properties of Perpendicular
Bisectors
G is the circumcenter of ∆ABC. By
the Circumcenter Theorem, G is
equidistant from the vertices of
∆ABC.
DG, EG, and FG are the
perpendicular bisectors of
∆ABC. Find GC.
GC = CB
GC = 13.4
Circumcenter Thm.
Substitute 13.4 for GB.

18. Example
Find GM.
GM = MJ GM = 14.5
MZ is a perpendicular bisector of ∆GHJ.
Find GK.
GK = KH GK = 18.6
KZ is a perpendicular bisector of ∆GHJ.
Find JZ.
JZ = GZ JZ = 19.9
Z is the circumcenter of ∆GHJ. By the
Circumcenter Theorem, Z is equidistant from
the vertices of ∆GHJ.

19. Example 2: Finding the Circumcenter of a Triangle
Find the circumcenter of ∆HJK with vertices
H(0, 0), J(10, 0), and K(0, 6).
Step 1 Graph. Step 2 Find equations for two
perpendicular bisectors.
The perpendicular bisector of HJ is x
= 5, and the perpendicular bisector
of HK is y = 3.
Step 3 Find the intersection of the
two equations.
(5, 3) is the circumcenter of ∆HJK.

20. Check It Out! Example 2
Find the circumcenter of ∆GOH with vertices
G(0, –9), O(0, 0), and H(8, 0) .
Step 1 Graph. Step 2 Find equations for two
perpendicular bisectors.
The perpendicular bisector of GO is
y = –4.5, and the perpendicular
bisector of OH is
x = 4.
Step 3 Find the intersection of the
two equations.
The lines intersect at (4, –4.5), the
circumcenter of ∆GOH.

21. A triangle has three angles, so it has three angle
bisectors. The angle bisectors of a triangle are
also concurrent. This point of concurrency is the
incenter of the triangle .

22. Unlike the circumcenter, the incenter is always inside
the triangle.

23. The incenter is the center of the triangle’s inscribed
circle. A circle inscribed in a polygon intersects
each line that contains a side of the polygon at
exactly one point.

24. Example 3A: Using Properties of Angle Bisectors
MP and LP are angle bisectors of ∆LMN. Find the
distance from P to MN.
MP and LP are angle bisectors of ∆LMN. Find
mPMN.