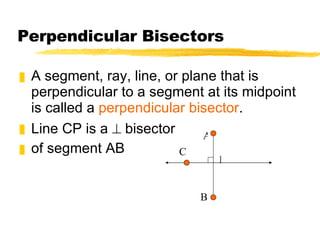
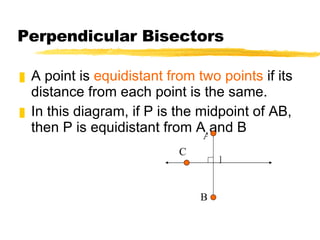
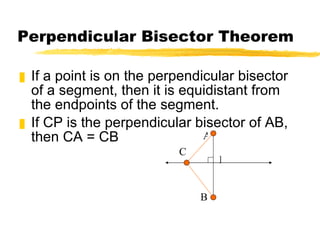
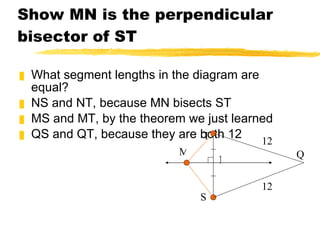
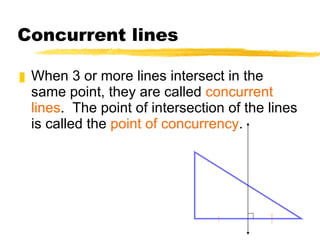
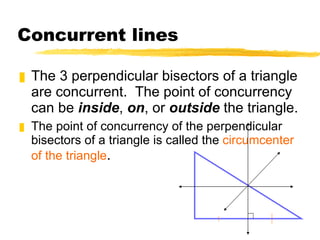
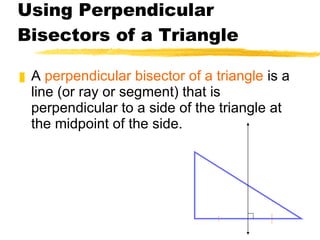
This document discusses perpendicular bisectors and angle bisectors of triangles. It defines perpendicular and angle bisectors and explains their properties. The key points are: 1) The perpendicular bisectors of a triangle are concurrent lines that intersect at a single point equidistant from the triangle's vertices, called the circumcenter. 2) The angle bisectors of a triangle are also concurrent lines intersecting at a single point equidistant from the triangle's sides, called the incenter. 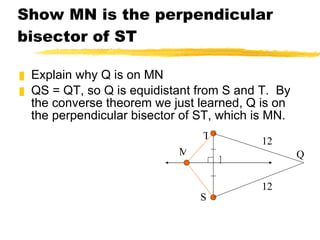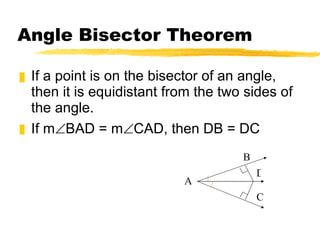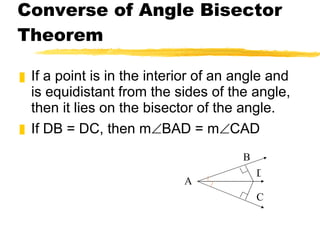3) Bisectors have useful properties for finding distances, such as if a point lies on a bisector it is equidistant from the sides of an angle or endpoints of a segment.

1. 5.1 & 5.2 Perpendiculars & Bisectors Objectives: - Use properties of perpendicular bisectors - Use properties of angle bisectors to find distances - Use bisectors in a triangle

2. Perpendicular Bisectors A segment, ray, line, or plane that is perpendicular to a segment at its midpoint is called a perpendicular bisector . Line CP is a  bisector of segment AB P A B C

3. Perpendicular Bisectors A point is equidistant from two points if its distance from each point is the same. In this diagram, if P is the midpoint of AB, then P is equidistant from A and B P A B C

4. Perpendicular Bisector Theorem If a point is on the perpendicular bisector of a segment, then it is equidistant from the endpoints of the segment. If CP is the perpendicular bisector of AB, then CA = CB P A B C

5. Converse of the Perpendicular Bisector Theorem If a point is equidistant from the endpoints of a segment, then it is on the perpendicular bisector of a segment. If CA = CB then C lies on the perpendicular bisector of AB. P A B C

6. Show MN is the perpendicular bisector of ST What segment lengths in the diagram are equal? NS and NT, because MN bisects ST MS and MT, by the theorem we just learned QS and QT, because they are both 12 N T S M Q 12 12

7. Show MN is the perpendicular bisector of ST Explain why Q is on MN QS = QT, so Q is equidistant from S and T. By the converse theorem we just learned, Q is on the perpendicular bisector of ST, which is MN. N T S M Q 12 12

8. Properties of Angle Bisectors The distance from a point to a line is defined as the length of the perpendicular segment from the point to the line. For example, the distance between Q and line m is QP P m Q

9. Properties of Angle Bisectors When a point is the same distance from one line as it is from another line, then the point is equidistant from the two lines (or rays or segments).

10. Angle Bisector Theorem If a point is on the bisector of an angle, then it is equidistant from the two sides of the angle. If m  BAD = m  CAD, then DB = DC A B D C

11. Converse of Angle Bisector Theorem If a point is in the interior of an angle and is equidistant from the sides of the angle, then it lies on the bisector of the angle. If DB = DC, then m  BAD = m  CAD A B D C

12. Look at p. 267 Example 3 You are given that B bisects  CAD and that  ACB and  ADB are right angles. What can you say about BC and BD? Because BC and BD meet AC and AD at right angles, they are perpendicular segments to the sides of  CAD. This implies that their lengths represent the distances from the point B to AC and AD. Because point B is on the bisector of  CAD, it is equidistant from the sides of the angle. So, BC = BD and you can conclude that segment BC ~= segment BD.

13. Do p. 267 1-7

14. Using Perpendicular Bisectors of a Triangle A perpendicular bisector of a triangle is a line (or ray or segment) that is perpendicular to a side of the triangle at the midpoint of the side.

15. Concurrent lines When 3 or more lines intersect in the same point, they are called concurrent lines . The point of intersection of the lines is called the point of concurrency .

16. Concurrent lines The 3 perpendicular bisectors of a triangle are concurrent. The point of concurrency can be inside , on , or outside the triangle. The point of concurrency of the perpendicular bisectors of a triangle is called the circumcenter of the triangle .

17. Concurrency of Perpendicular Bisectors of a Triangle Theorem The perpendicular bisectors of a triangle intersect at a point that is equidistant from the vertices of the triangle. See picture on p. 273

18. Useful Stuff! See page 273, Example 1

19. Using Angle Bisectors of a Triangle An angle bisector of a triangle is a bisector of an angle of the triangle. The 3 angle bisectors are concurrent. The point of concurrency is called the incenter of the triangle and always lies inside the triangle.

20. Concurrency of Angle Bisectors of a Triangle Theorem The angle bisectors of a triangle intersect at a point that is equidistant from the sides of the triangle. See picture on page 274.

21. Look at Example 2, p. 274 The angle bisectors of ∆ MNP meet at point L. What segments are congruent? By the theorem we just learned, the 3 angle bisectors of a triangle intersect at a point that is equidistant from the sides of a triangle. So, LR ~= LQ ~= LS

22. Look at Example 2, p. 274 Find LQ and LR Use the Pythagorean Theorem to find LQ in ∆LQM (LQ) 2 + (MQ) 2 = (LM) 2 (LQ) 2 + 15 2 = 17 2 (LQ) 2 + 225 = 289 (LQ) 2 = 64 LQ = 8 Because LQ ~= LR, LR also = 8

23. Do p. 275 1-4 Homework: Worksheets