Il documento tratta della derivata di una funzione, descrivendo il significato geometrico e il calcolo della retta tangente in un punto specifico. Viene introdotto il concetto di rapporto incrementale e come esso rappresenti il tasso di variazione della funzione. Inoltre, si discute la continuità e la derivabilità delle funzioni, includendo punti di non derivabilità e regole di derivazione.

1. DERIVATA DI UNA FUNZIONE IN UN PUNTO
SIGNIFICATO GEOMETRICO. EQUAZIONE DELLA RETTA TANGENTE
AL GRAFICO NEL PUNTO DI TANGENZA.
REGOLE DI DERIVAZIONE. CONTINUITA’ E DERIVABILITA’
PUNTI DI NON DERIVABILITA’
Angela Donatiello
1

2. A (x1,y1) = (c, f(c))
B(x2,y2) = (c+h, f(c+h))
m=
y 2  y1 y

 tg
x 2  x1 x
dove  è l’angolo che la retta forma
con l’asse delle ascisse valutato in
senso antiorario.
RAPPORTO INCREMENTALE o
TASSO DI VARIAZIONE
y f (c  x )  f (c) f (c  h )  f (c)


x
x
h
Angela Donatiello
2

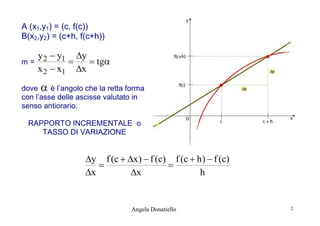
3.  Esso prende il nome di rapporto incrementale, in quanto è il rapporto tra
l’incremento della variabile dipendente e quello della variabile
indipendente.
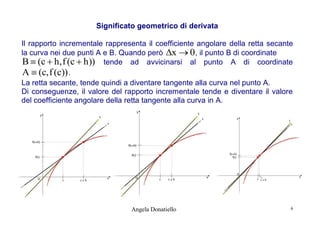
 Il rapporto incrementale corrisponde al coefficiente angolare della retta
secante la curva nei due punti A e B
 Esprime il tasso di variazione della funzione relativo all’intervallo [c,c+h]
 E’ un tasso di crescita se è positivo, un tasso di decrescita se negativo
 Si può interpretare anche come velocità media di variazione della
funzione nell’intervallo assegnato
 Se la funzione è una retta esso è costante, altrimenti varia, al variare
dell’intervallo
Esempio. Il tasso di crescita di una popolazione malthusiana è un rapporto
incrementale:
N( t )  N( t  1)
nm
N( t  1)
Angela Donatiello
3

4. Esempio. Velocità media di un corpo. La velocità media è rappresentata dal
rapporto tra lo spazio percorso e il tempo impiegato per percorrerlo,
indipendentemente dalla legge oraria considerata.
s s( t 2 )  s( t1)
vmedia 

t
t 2  t1
E’ interessante valutare anche la velocità istantanea di un corpo.
Esempio. Controllo della velocità: tutor in autostrada e autovelox.
 Tutor misura la velocità media:
s s( t 2 )  s( t1)
vmedia 

t
t 2  t1
 L’autovelox misura la velocità istantanea, ossia una velocità media con
l’intervallo di tempo
t  0
s
s( t 2 )  s( t1)
vis tan tan ea  lim
 lim
t 2  t1
t 0 t t 0
Angela Donatiello
4

5. Data una funzione y  f ( x ) , il limite del
rapporto incrementale,
y
f ( c  h )  f ( c)
lim
 lim
h
x 0 x h 0
se esiste ed è finito
si chiama derivata della funzione nel
punto c e si indica con il simbolo f ' (c) o
df
(c)
dx
Esempio. Accelerazione media e accelerazione istantanea. (8.1.7)
Angela Donatiello
5

6. Significato geometrico di derivata
Il rapporto incrementale rappresenta il coefficiente angolare della retta secante
la curva nei due punti A e B. Quando però x  0 , il punto B di coordinate
B  (c  h, f (c  h )) tende ad avvicinarsi al punto A di coordinate
A  (c, f (c)) .
La retta secante, tende quindi a diventare tangente alla curva nel punto A.
Di conseguenze, il valore del rapporto incrementale tende e diventare il valore
del coefficiente angolare della retta tangente alla curva in A.
Angela Donatiello
6

7. f ' ( c) 
y
f ( c  h )  f ( c)
lim
 lim
h
x 0 x h 0
Il valore
derivata della funzione nel punto c, coincide
con il coefficiente angolare della retta
tangente alla curva in c.
Equazione della retta tangente
Ricordiamo l’equazione del fascio proprio di rette di centro un dato punto P
y  y 0  m( x  x 0 )
 y  f (c)  m( x  c)
m  f ' (c)
 y  f (c)  f ' (c)( x  c)
Angela Donatiello
7

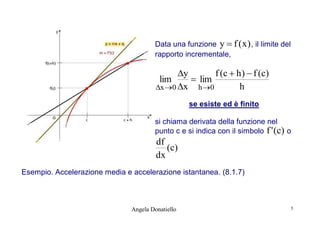
8. Punto stazionario: Data la funzione y  f ( x ) e un suo punto x = c, se
f ' (c)  0 allora si dice x = c è punto stazionario, ovvero un punto a tangente
orizzontale.
Derivata destra e sinistra
f ( c  h )  f ( c)
f ' (c)  lim
h
h 0
derivata sinistra nel punto c
f ( c  h )  f ( c)
f ' (c)  lim
h
h 0
derivata destra nel punto c


Una funzione si definisce derivabile in un punto c se esistono finite le derivate
destra e sinistra e sono uguali.
Una funzione si definisce derivabile in un intervallo chiuso [a,b] se è
derivabile in tutti i suoi punti interni e se esistono finite la derivata destra in a e la
derivata sinistra in b.
Angela Donatiello
8

9. Continuità e derivabilità
Teorema. Se una funzione
punto è anche continua.
y  f ( x ) è derivabile in un punto x0 allora in quel
f (x0  h)  f (x0 )
Hp:  finito lim
h
h 0
Th:
lim f ( x )  f ( x 0 )
x x 0
Dim.
f (x0  h)  f (x0 )
f (x0  h)  f (x0 )  f (x0  h)  f (x0 )  f (x0 ) 
h
h
Calcolo il limite per h  0 di entrambi i membri, tenendo conto del fatto che il
limite della somma è la somma dei limiti, il limite del prodotto è il prodotto dei
limiti e il limite di una costante è la costante stessa.
f (x0  h)  f (x0 )
lim f ( x 0  h )  lim f ( x 0 ) 
h
h
h 0
h 0
Angela Donatiello
9

10. f (x 0  h)  f (x 0 )
f (x 0  h)  f (x 0 )
 lim f ( x 0 )  lim
 h  f ( x 0 )  lim
h
h
h
h 0
h 0
h 0
Ricordiamo l’ipotesi:
f (x0  h)  f (x0 )
 f ' (x0 )
h
h 0
 finito lim
Allora
(*)
f (x 0  h)  f (x 0 )
lim
 h  f ' (x0 )  0  0
h
h 0
lim f ( x 0  h )  f ( x 0 )  f ' ( x 0 )  0  f ( x 0 )
h 0
Pongo
x0  h  x
Sostituendo nella (*)
h  0  x  x0
lim f ( x )  f ( x 0 ) cioè la funzione è continua in x0.
se
x x 0
Angela Donatiello
10

11. Attenzione: Non vale il viceversa!!!! Il teorema non si può invertire!!
E’ cioè possibile trovare funzioni continue in un punto, ma non derivabili in tale
punto.
Controesempio. La funzione valore assoluto
 x x0
f ( x ) | x | 
 x x  0
Proviamo che in x = 0 è continua, ma non
derivabile.
1)
lim  f ( x )  lim  | x | lim   x  0
x 0
x 0
x 0
x 0
x 0
x 0
lim  f ( x )  lim  | x | lim  x  0  f (0)
Pertanto possiamo affermare che è continua in x = 0
Angela Donatiello
11

12. 2) Valutiamo ora la derivata destra e la derivata sinistra:
f (0  h )  f (0)
|0 h ||0|
|h|
h
f ' (0)  lim
 lim
 lim
 lim
 1
h
h
h 0
h 0
h 0 h
h 0 h

f ' (0)  lim
h 0 



f (0  h )  f (0)
|0h||0|
|h|
h
 lim
 lim
 lim  1
h
h
h 0
h 0 h
h 0 h



Pertanto la derivata destra e la derivata sinistra in x = 0 esistono finite, ma sono
diverse, la funzione non è derivabile in x = 0 e si dice che essa ha in x = 0 un
punto angoloso.
Angela Donatiello
12

13. Punti di non derivabilità
Punti angolosi
E' un punto in cui la derivata destra e la derivata sinistra esistono finite,o
almeno una delle due è finita, ma sono diverse. In questo caso la curva nel
punto ha due tangenti con pendenza diversa.
f ' (c)  f ' (c)
Angela Donatiello
13

14. Cuspidi
Un punto di cuspide è un punto in cui la derivata destra e la derivata sinistra
sono infinite, ma con segno diverso.
Cuspide verso il basso:
f ' (c)  
f ' (c)  
Cuspide verso l’alto:
f ' (c)  
f ' (c)  
Angela Donatiello
14

15. Flessi a tangente verticale
Un punto di flesso a tangente verticale è un punto in cui la derivata destra e la
derivata sinistra sono infinite con lo stesso segno. In questo caso la retta
tangente alla curva esiste ed è una retta parallela all’asse y di equazione x = c.
f ' (c)  
f ' (c)  
f ' (c)  
f ' (c)  
Angela Donatiello
15

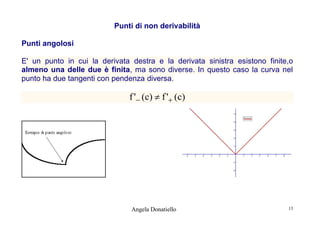
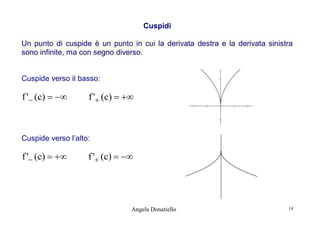
16. f (x  h)  f (x)
Funzione derivata: f ' ( x ) : x  lim
h
h 0
REGOLE DI DERIVAZIONE






D[k  f ( x )]  k  f ' ( x )
D[f ( x )  g( x )]  f ' ( x )  g' ( x )
D[f ( x )  g( x )]  f ' ( x )g( x )  f ( x )g' ( x )
D[f ( x )]n  n[f ( x )]n 1  f ' ( x )
1
f ' (x)
D

f (x)
[f ( x )]2
f ( x ) f ' ( x )g ( x )  f ( x )g ' ( x )
D

g( x )
[g( x )]2
Angela Donatiello
16

17. Derivate fondamentali
(dim. svolte in aula)








D(k )  0
D( x )  1
D(senx)  cos x
D(a x )  a x ln a
1
D(log a x )  log a e
x
1
D( tgx ) 
 1  tg 2 x
cos2 x
1
D(arcsin x ) 
1  x2
1
D(arctgx ) 
1  x2
D(cos x )  senx
D(e x )  e x
1
D(ln x ) 
x
1
D( x ) 
2 x
D(arccos x )  
Angela Donatiello
1
1  x2
17

18. Derivata della funzione inversa
1
Teorema. Sia y  f ( x ) definita e invertibile in un intervallo I e sia x  f ( y) la
sua inversa. Se y  f ( x ) è derivabile in ogni punto di I, con derivata diversa da
1
zero, allora anche x  f ( y) è derivabile e vale la relazione:
1
D[f ( y)] 
f ' (x)
1
Applicazioni
D(arcsin x ) 
D(arctgx ) 
1
1 x
2
D(arccos x )  
1
1  x2
1
1  x2
Angela Donatiello
18

19. Derivata della funzione composta
Teorema. Se la funzione g è derivabile nel punto x e la funzione f è derivabile in
z  g( x ) , allora la funzione composta y  f (g( x )) è derivabile in x e la sua
derivata è il prodotto delle derivate di f rispetto a z e di g rispetto a x.
df dz
D[f (g( x ))]  f ' (z)  g' ( x )  
dz dx
con
z  g( x )
y  (2x 3  3x 2  x  1)4 in tal caso
z  g( x )  2x3  3x 2  x  1
y  f ( z)  z 4
df dz
Dy    4z3  z'  4(2x 3  3x 2  x  1)3  (6x 2  6x  1)
dz dx
Esempio.
Esempio.
y  ln sen( x  2)
4
 y' 
Angela Donatiello
1
sen ( x 4  2)
 cos(x 4  2)  4x 3
19

20. Esempio.
y  arctg 3x
1
1
1
 y' 


3 
2 arctg 3x 1  3x 2 3x

3
4(1  3x ) 3xarctg 3x
x
2
Esempio. y  4arcsen  x 4  x
2
1
1
1
2
y'  4 
  4x x
 (2 x ) 
2 2
2
x
2 4x
1
4
1
x2
4
x2
 4
  4  x2 

 4  x2 

2 2
2
2
2
4x
4x
4x
4x
2

4  4  x2  x2
4  x2

2(4  x 2 ) 4  x 2
(4  x 2 )
 2 4  x2
Angela Donatiello
20

21. Derivate di ordine superiore al primo
Data la funzione y  f ( x ) , la sua derivata y'  f ' ( x ) è una funzione della
variabile x, della quale a sua volta è possibile calcolare la derivata. Tale derivata
prende il nome di derivata seconda y' '  f ' ' ( x ) . In modo analogo si definisce la
derivata terza, come la derivata della derivata seconda e così via.
La derivata di una funzione è anche detta derivata prima.
y  f ( x )  x 3  3x  2
y' '  6 x
y'  3x 2  3
Esempio.
Angela Donatiello
y' ' '  6
y ( 4)  0
21

22. Derivate di funzioni definite per casi o contenente valori assoluti
f ( x ) | ln x |
Determino il dominio della funzione
x  0
C.E. 
x0
 x 0
D  0,
Poi valuto il segno dell’argomento del modulo
x  0
x  0
x  0


ln x  0   x  0
 x  0  
 x 1
x  1
ln x  ln 1  x  1


Angela Donatiello
22

23. Si deduce che l’argomento è
ln x  0  x  1
ln x  0  0  x  1
Posso quindi scrivere la funzione per casi:
x 1
ln x
f ( x ) | ln x |  
 ln x
0  x 1
Determino ora la funzione derivata
1
1
 1
 x  2 x  2x

f ' (x)  
 1  1   1
 x 2 x
2x

1
x 1
 2x
 
 1
0  x 1
 2x
Angela Donatiello
x 1
0  x 1
23

24. Attenzione!!!!!! Devo inizialmente escludere gli estremi, in quanto va controllato
se in essi la funzione derivata esiste oppure no e pertanto vanno eventualmente
esclusi dal dominio di derivabilità.
Cosa succede in x = 1 ?
Valutiamo la derivata destra e la derivata sinistra. Se esse risultano diverse o
non esistono o sono infinite, allora la funzione iniziale y = f(x) non risulta
derivabile in x = 1 e dunque tale punto va escluso dal dominio di derivabilità.
f ' (1) 
1
2
f ' (1)  
1
2
f ' (1)  f ' (1)
finite
Pertanto la funzione in x = 1 non è derivabile e presenta un punto angoloso
D'  0,1  1,
Si osserva che
dominio di derivabilità
D'  D
Angela Donatiello
24

25. Determiniamo le due semirette tangenti in x = 1
f (1) | ln 1 | 0
 P(1;0)
1
1
1
f ' (1)   t  : y  x 
2
2
2
 y  0  m( x  1)
1
1
1
f ' (1)    t  : y   x 
2
2
2
Angela Donatiello
25

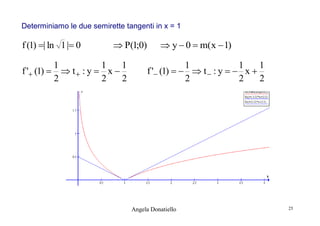
26. Esercizi.
 Determina la funzione derivata delle seguenti funzioni contenente moduli.
y | x 2  6x |
y  xe|x|
y  ln(| x  1 | 1)
x
 Determina l’equazione della retta tangente alla curva y  e x 1 nel suo
punto di intersezione con l’asse y.
[y = - x + 1 ]

ax 2  bx  c
Determina i coefficienti dell’equazione y 
sapendo che il
4x  d
 1
grafico corrispondente passa per il punto 1;  , nell’origine ha per
 3
tangente la retta y  2x ed inoltre si ha che lim f ( x )  
x
Angela Donatiello
1
4
26

27.  Determina i punti di discontinuità e di non derivabilità delle seguenti
funzioni e indicane il tipo.
e|x|

f ( x )  1  x

x  2
x 1
x 1
[x=1 punto di discontinuità I specie; x=0 punto angoloso; x=2 p. disc. II specie]
3
f (x)  x 2  x3
[x=0 cuspide; x=1 flesso a tangente verticale]
Angela Donatiello
27

28.  Trova a e b, in modo che la funzione sia continua e derivabile in tutto R
2

a cos x  bsenx

f (x)   2

 x 1
a  x 2  3

f (x)  
b ln x  (2a  1) x

x0
x0
[a= -2, b = 2]
x 1
x 1
Angela Donatiello
[a =1, b = - 5/2]
28