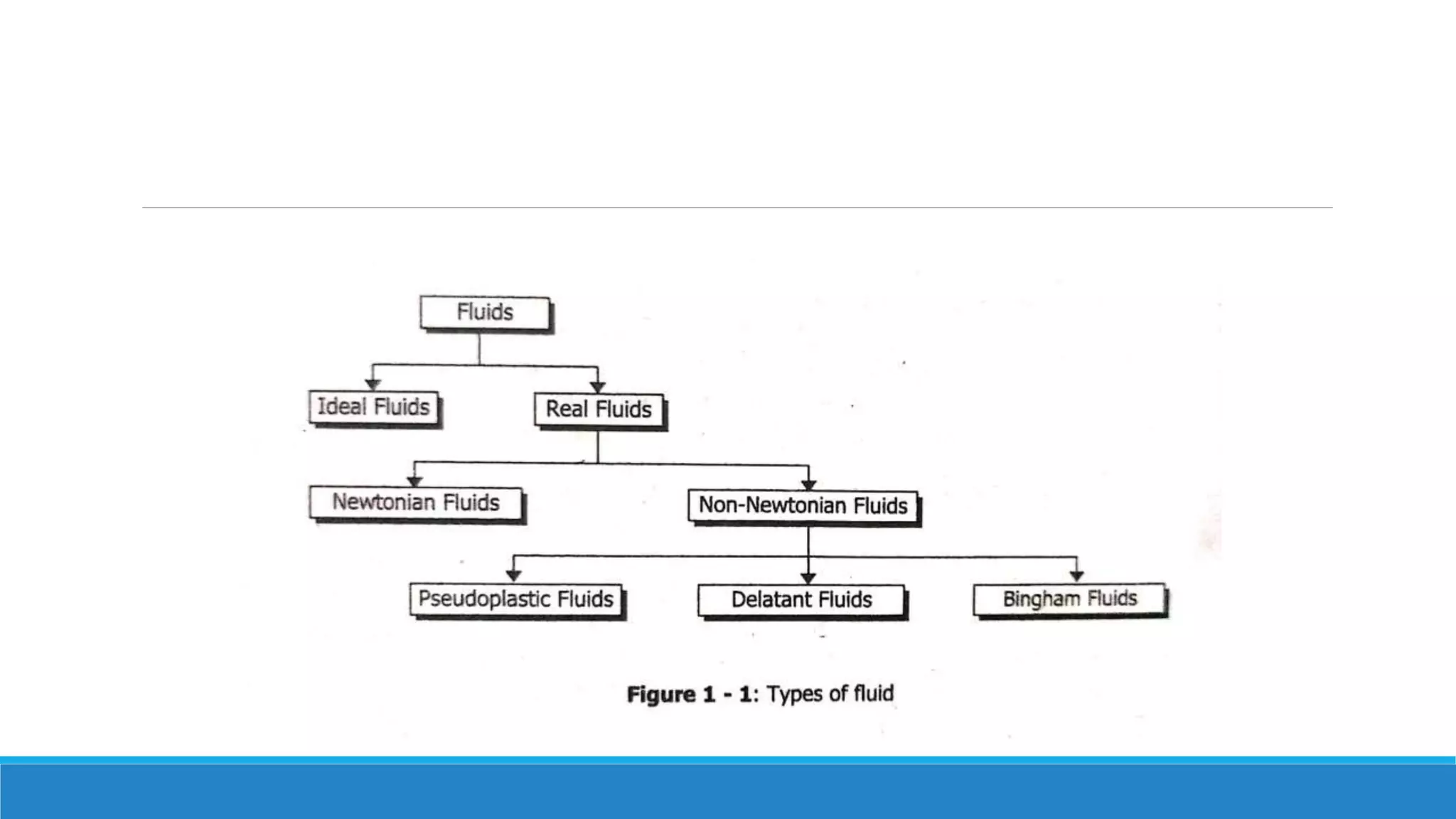
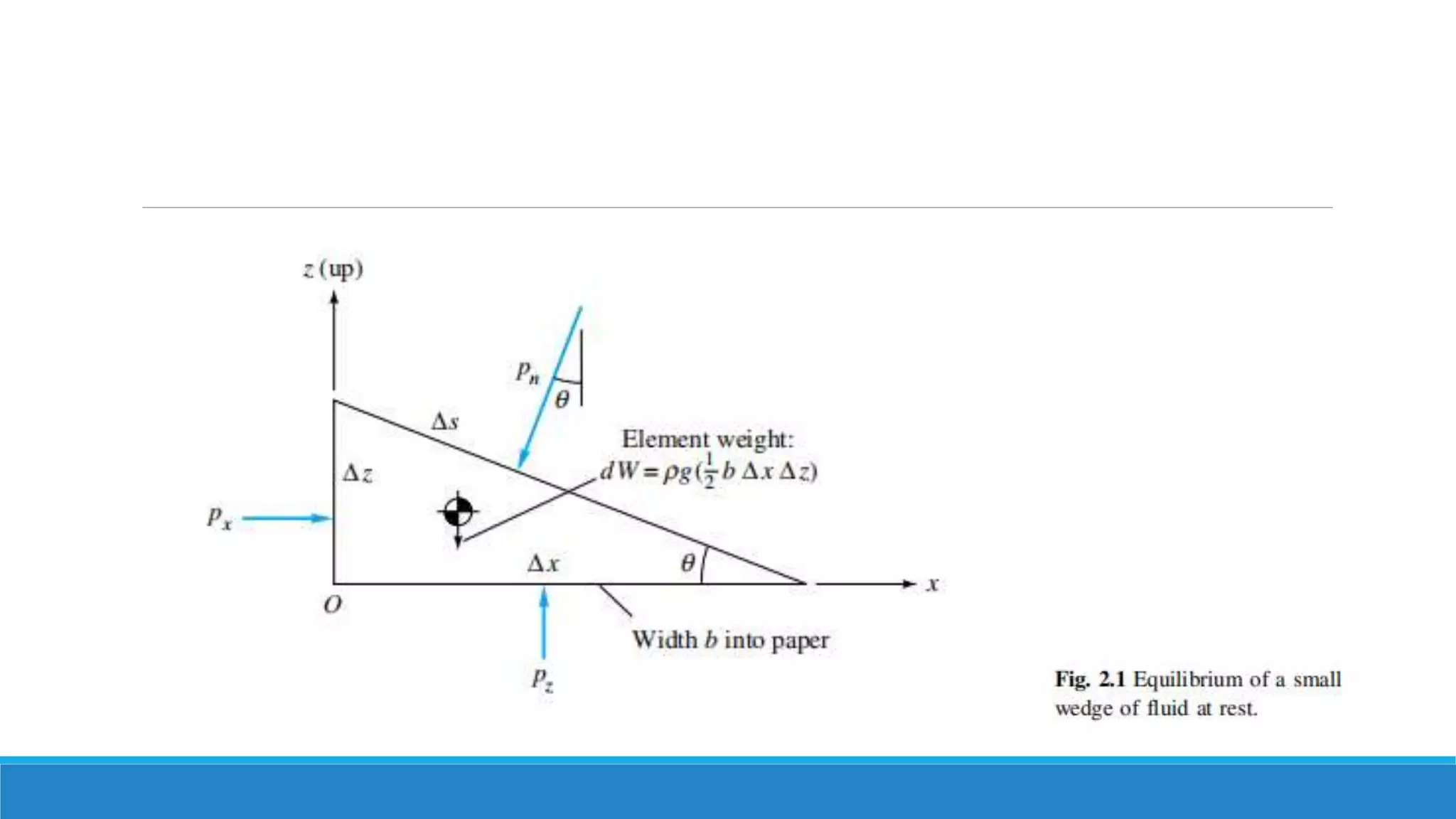
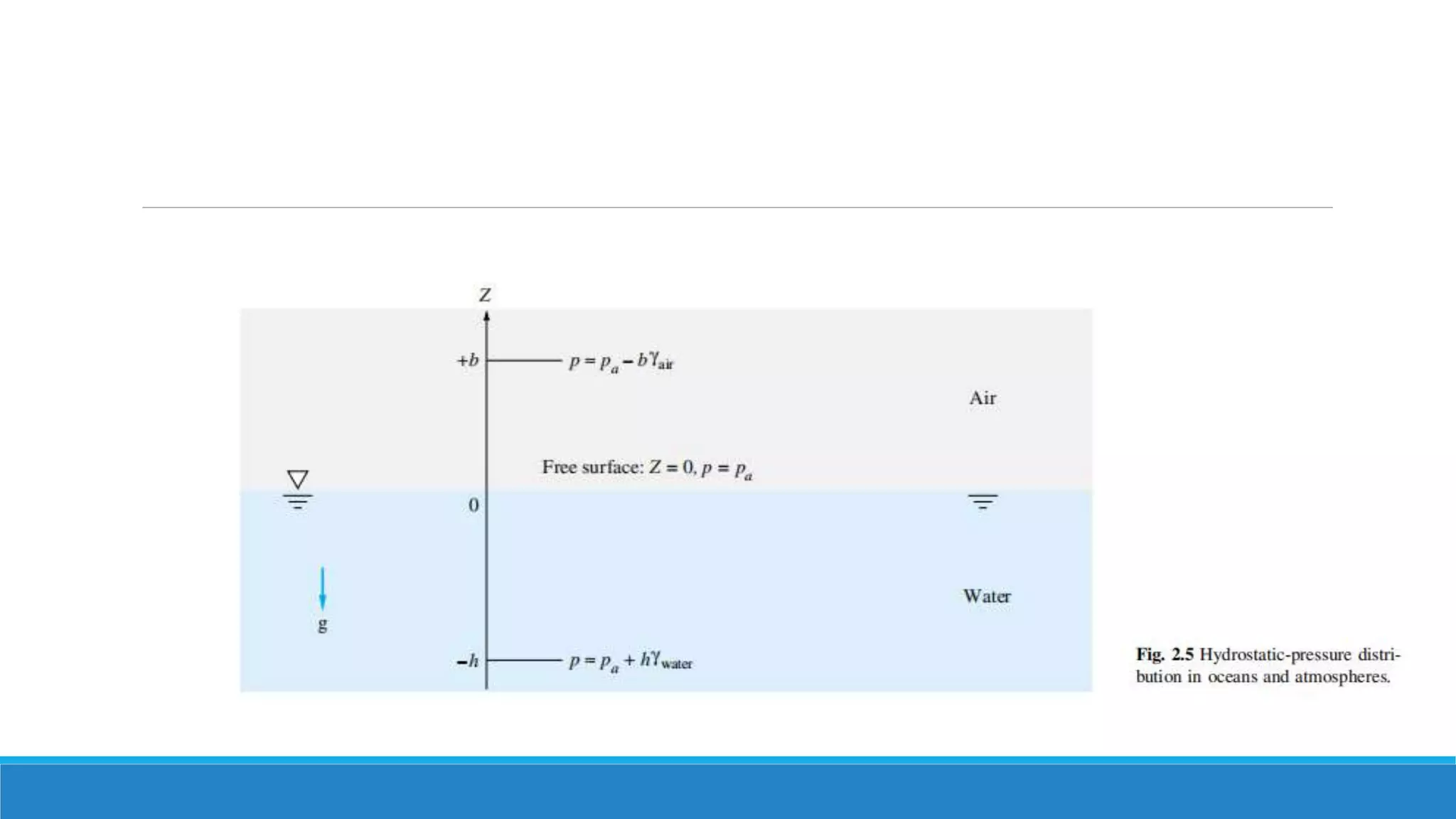
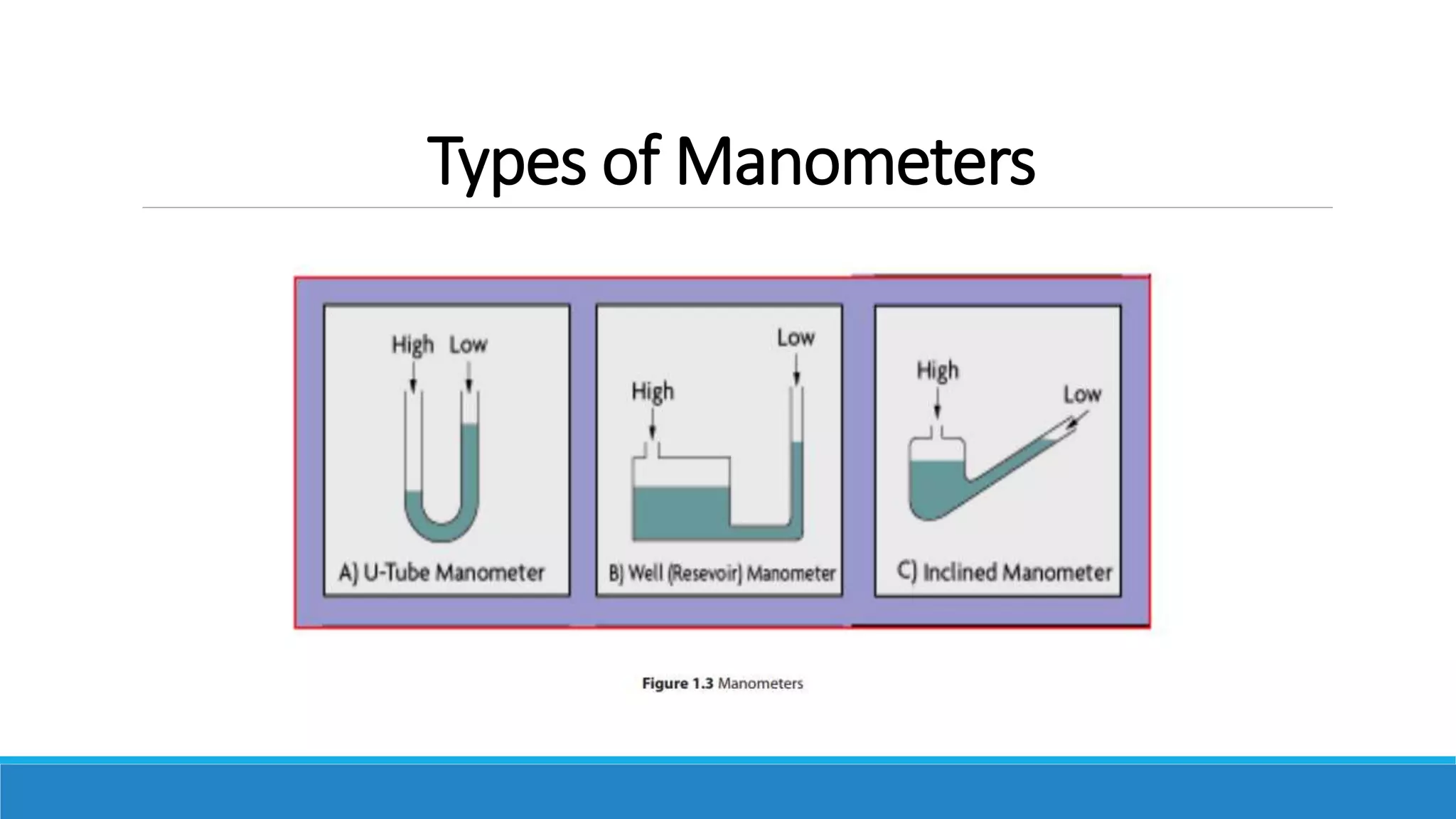
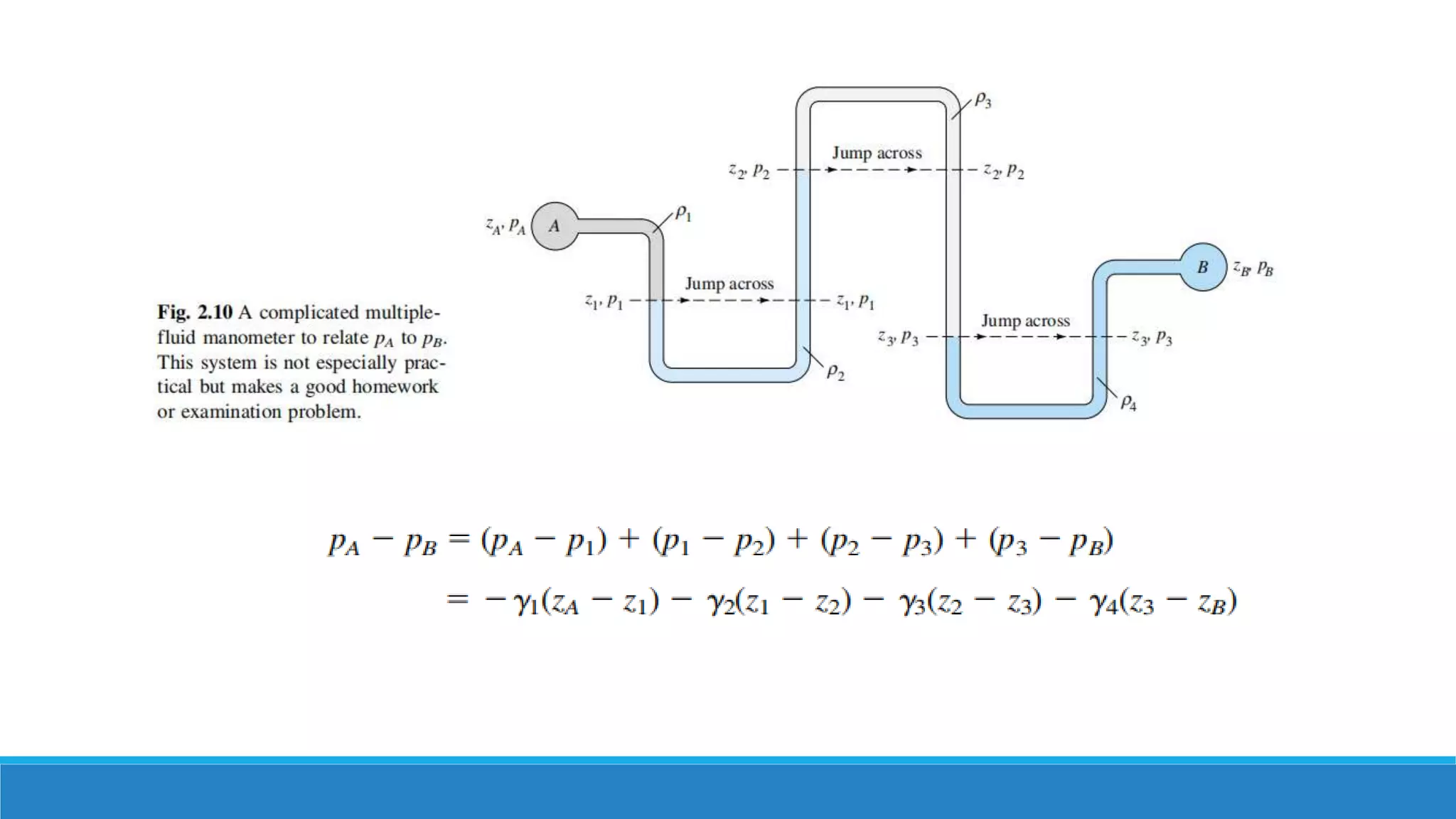
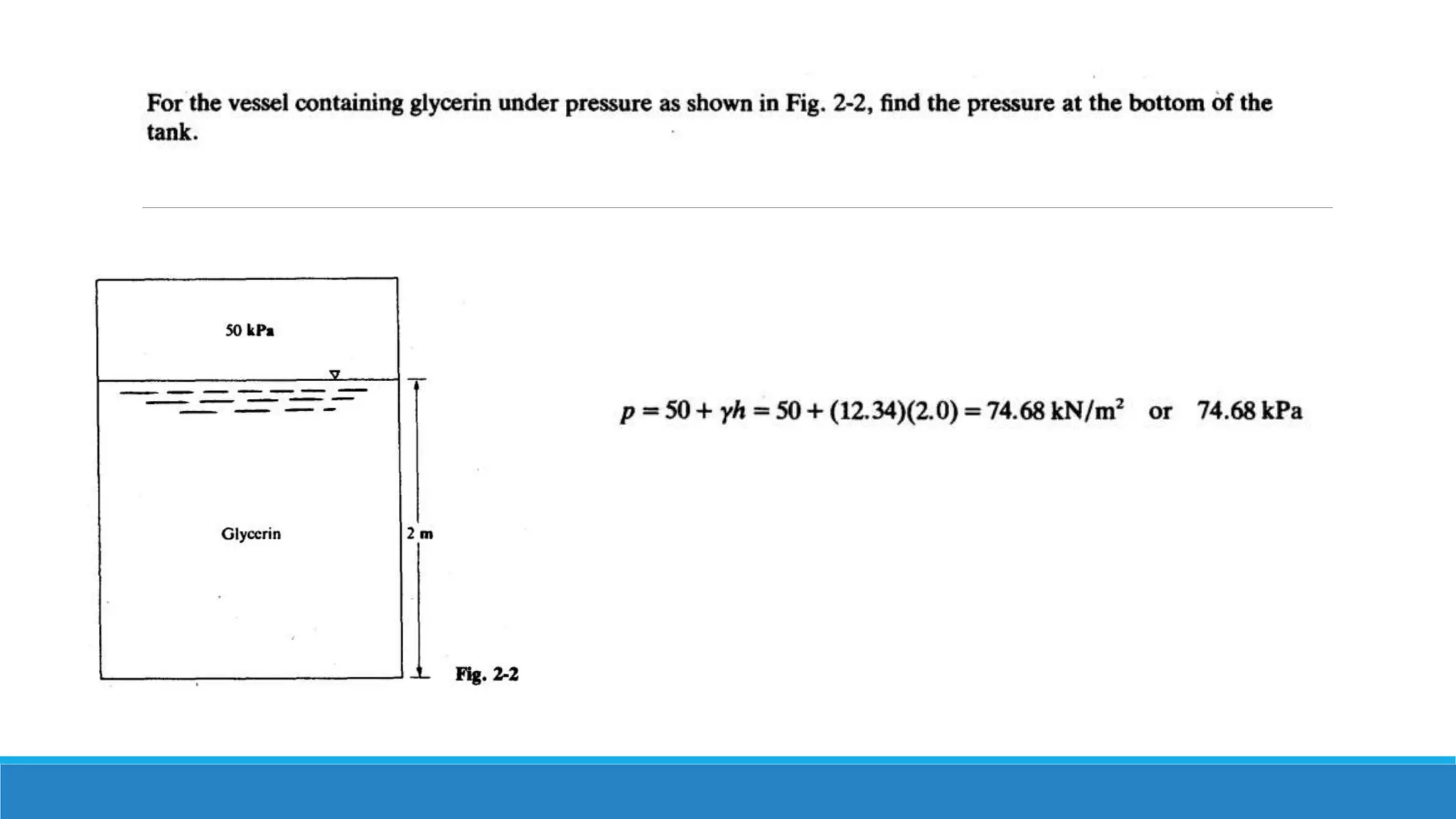
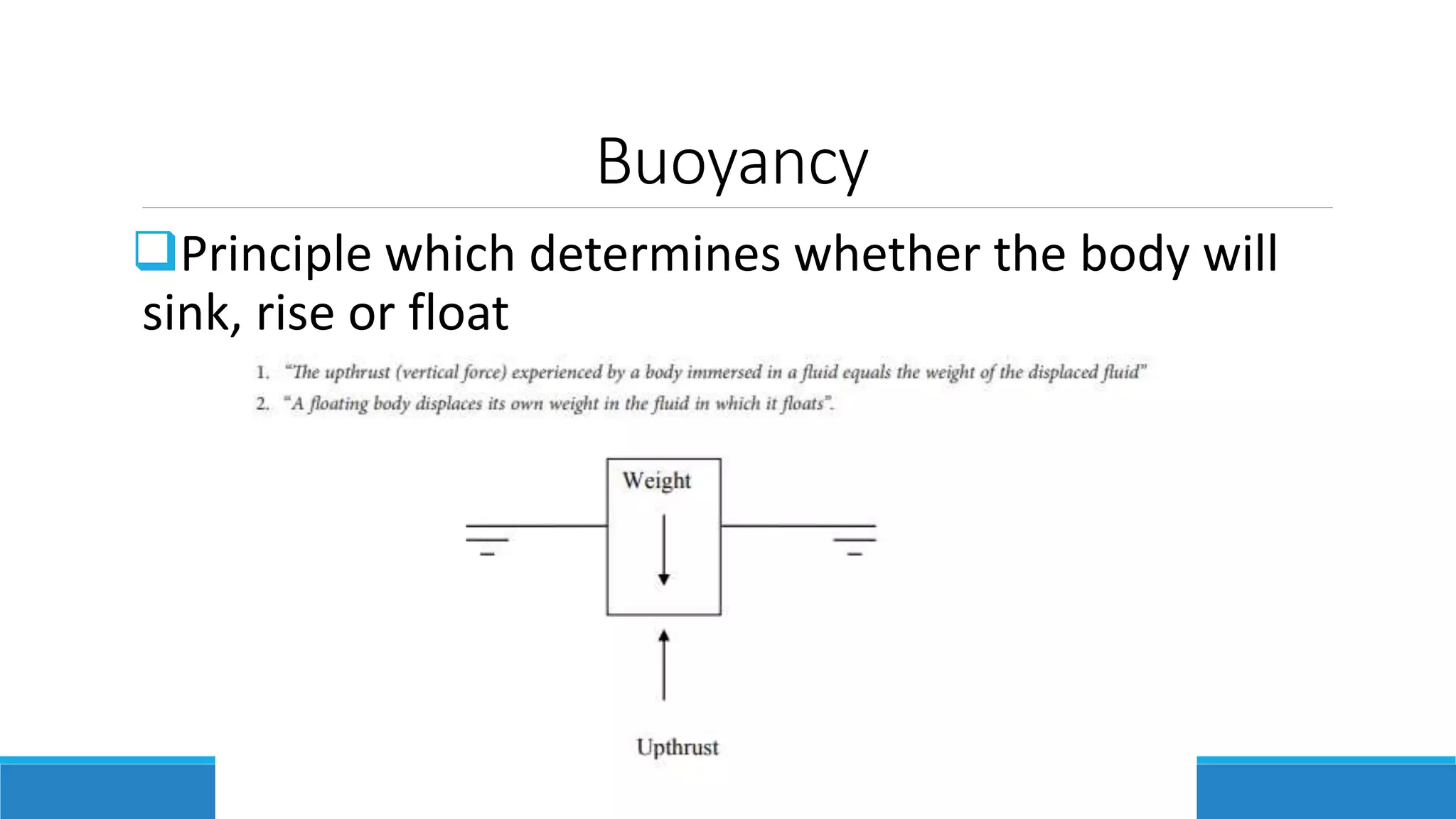
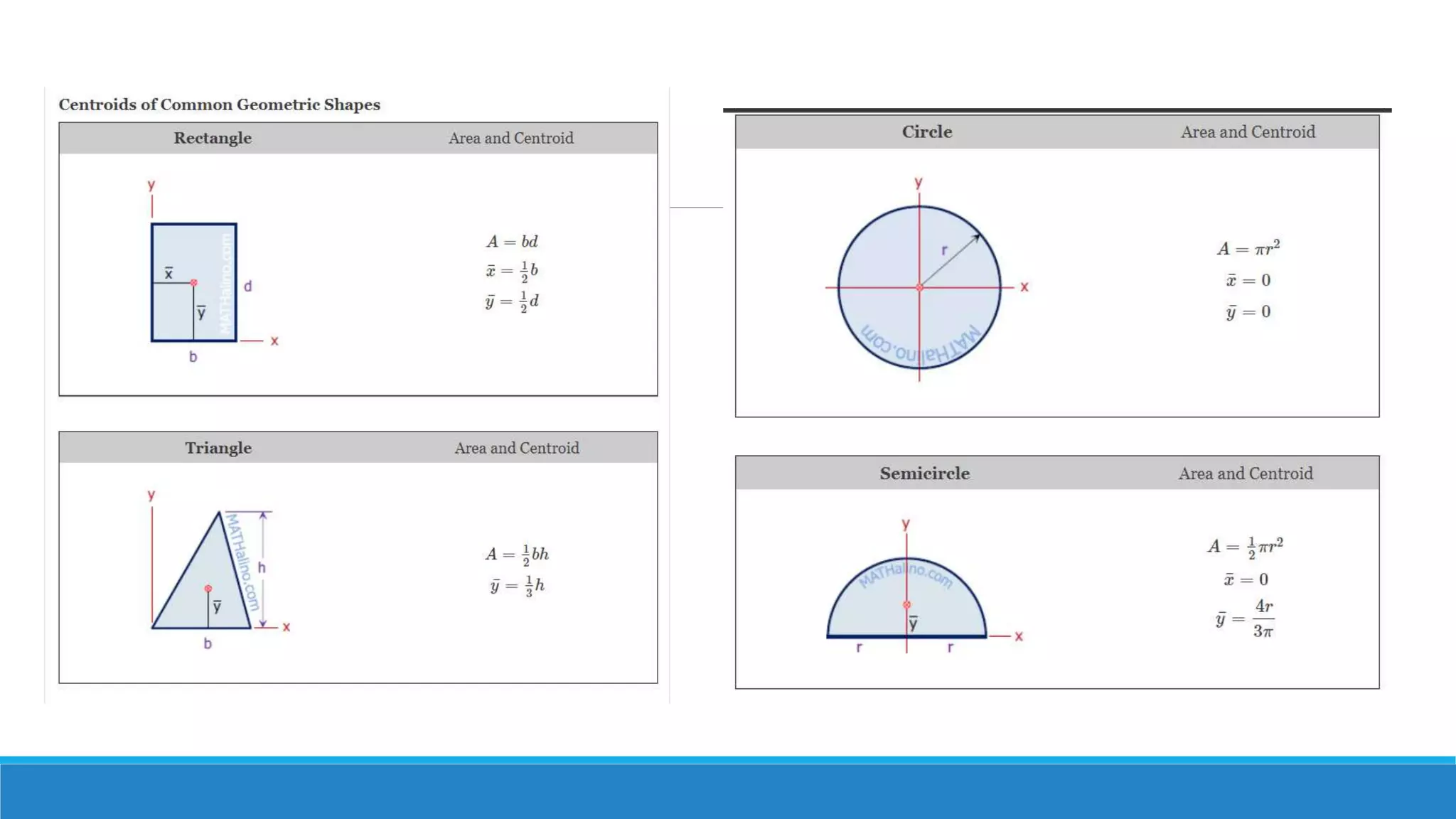
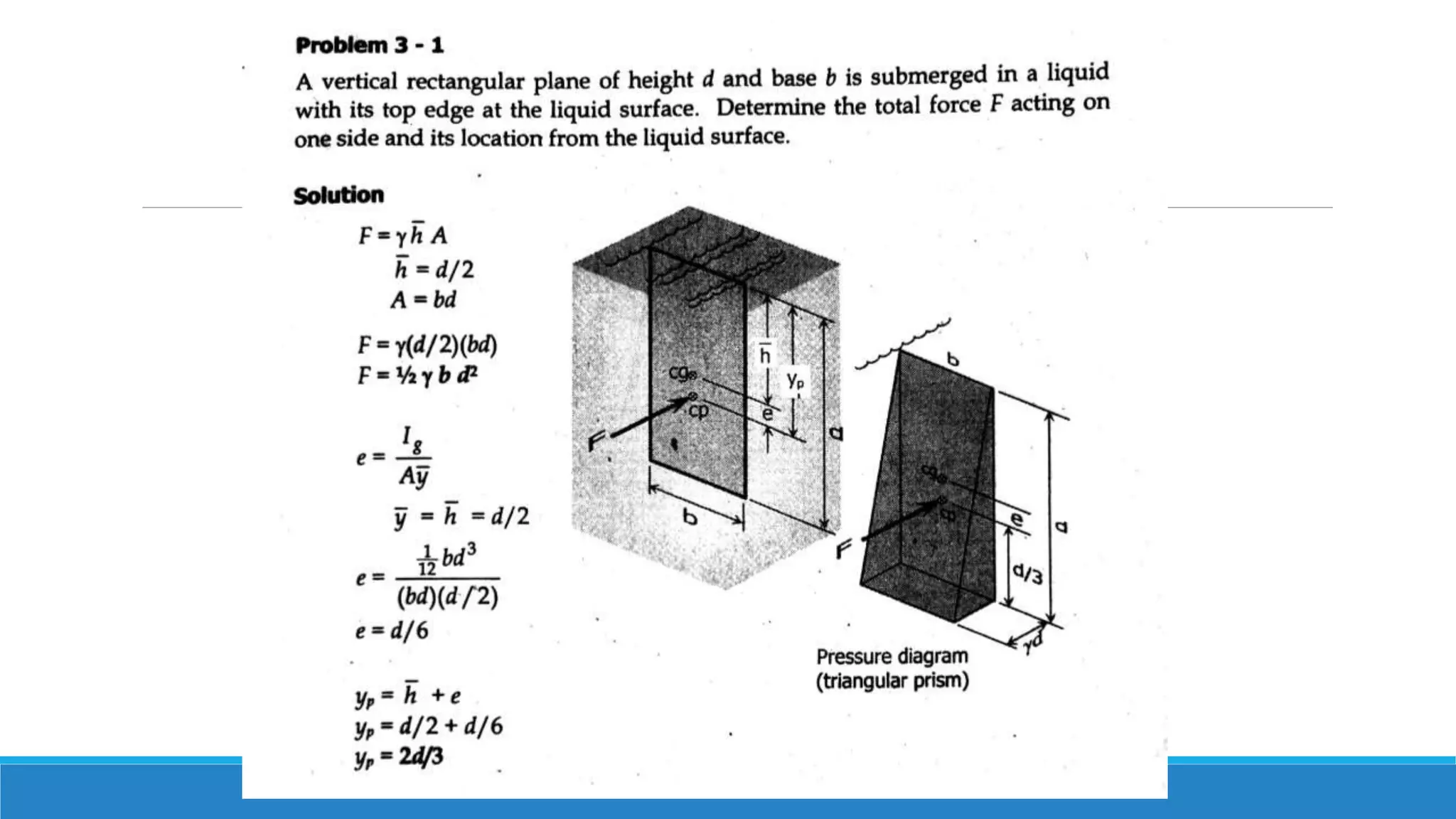
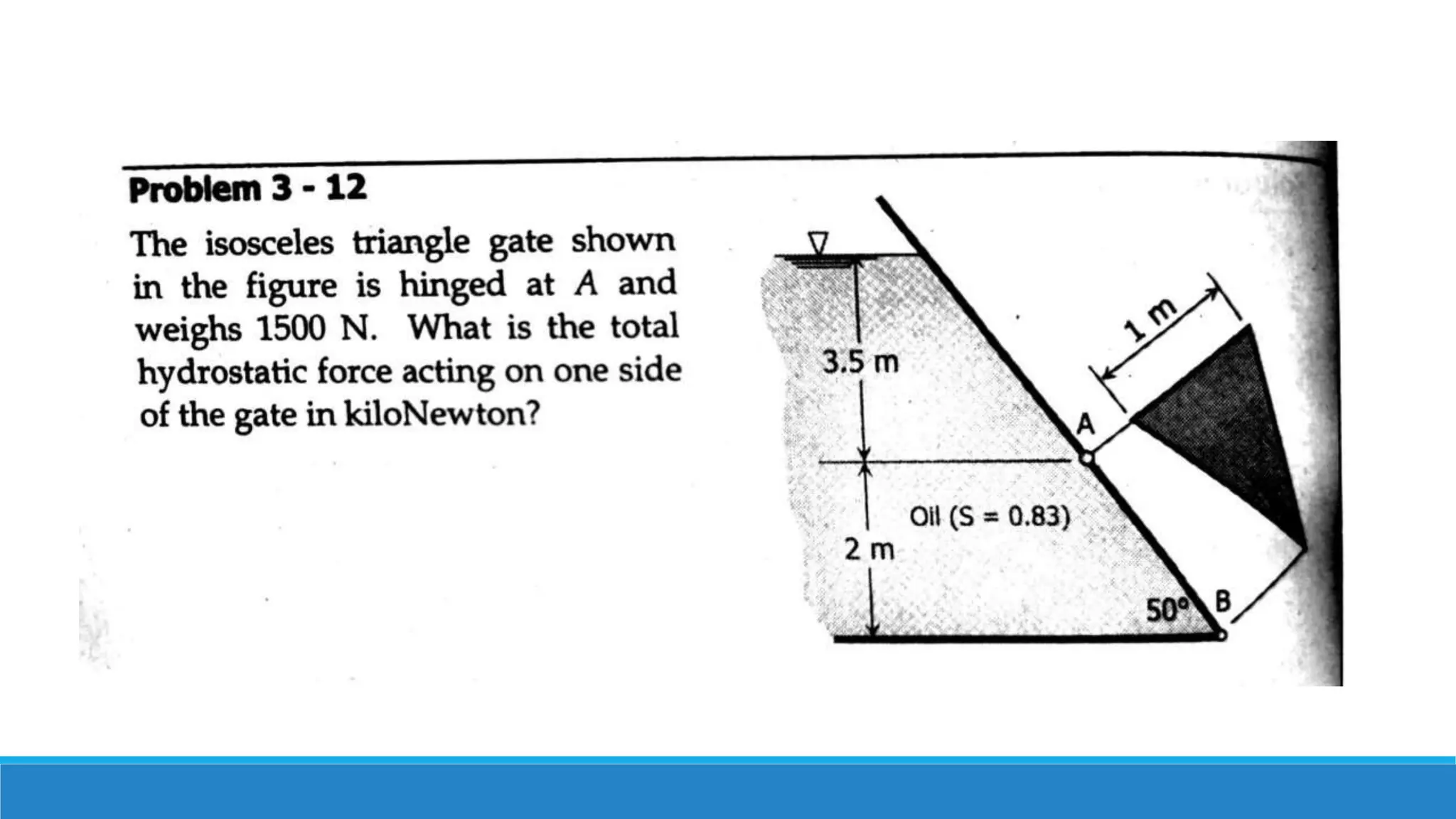
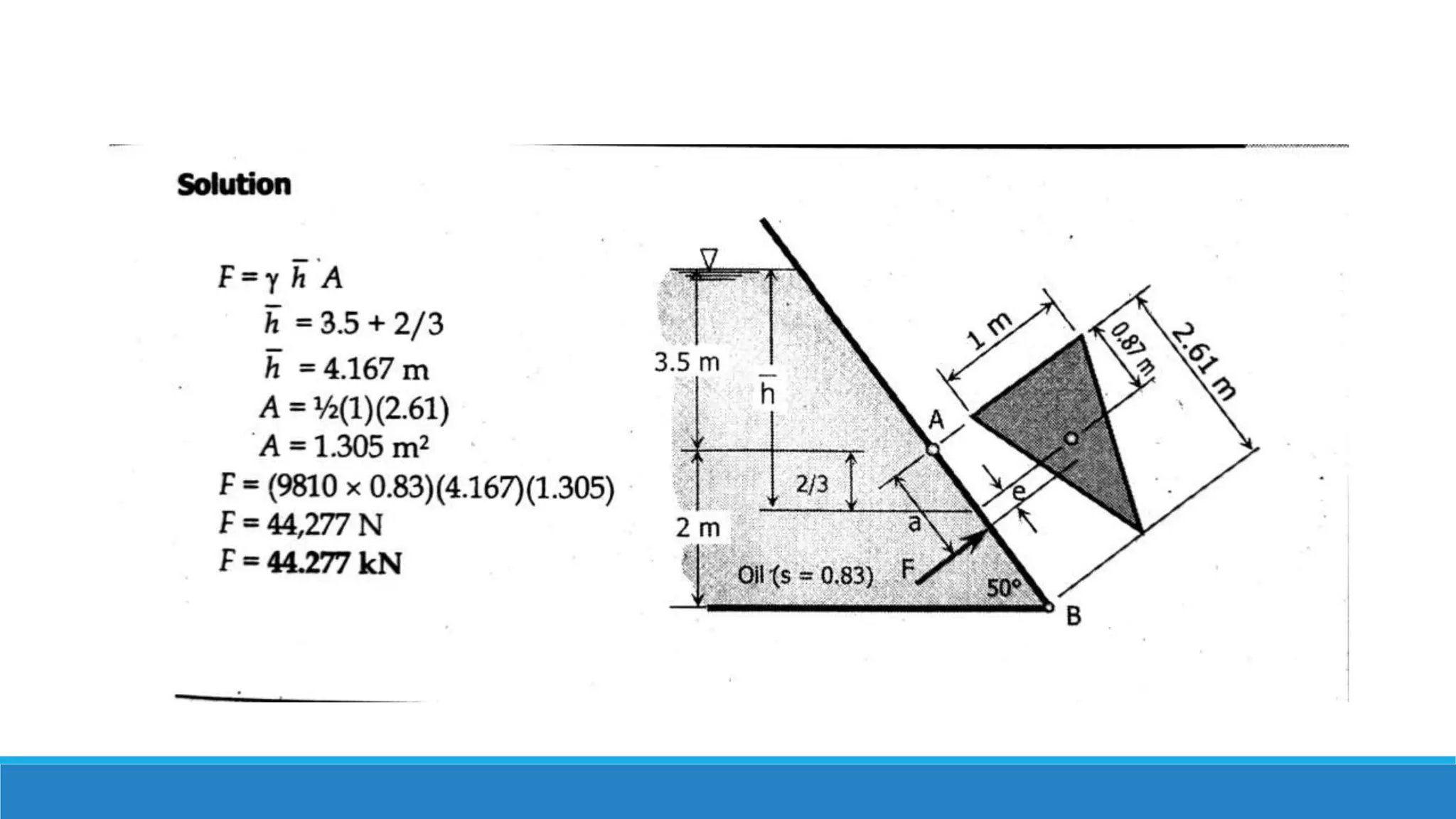
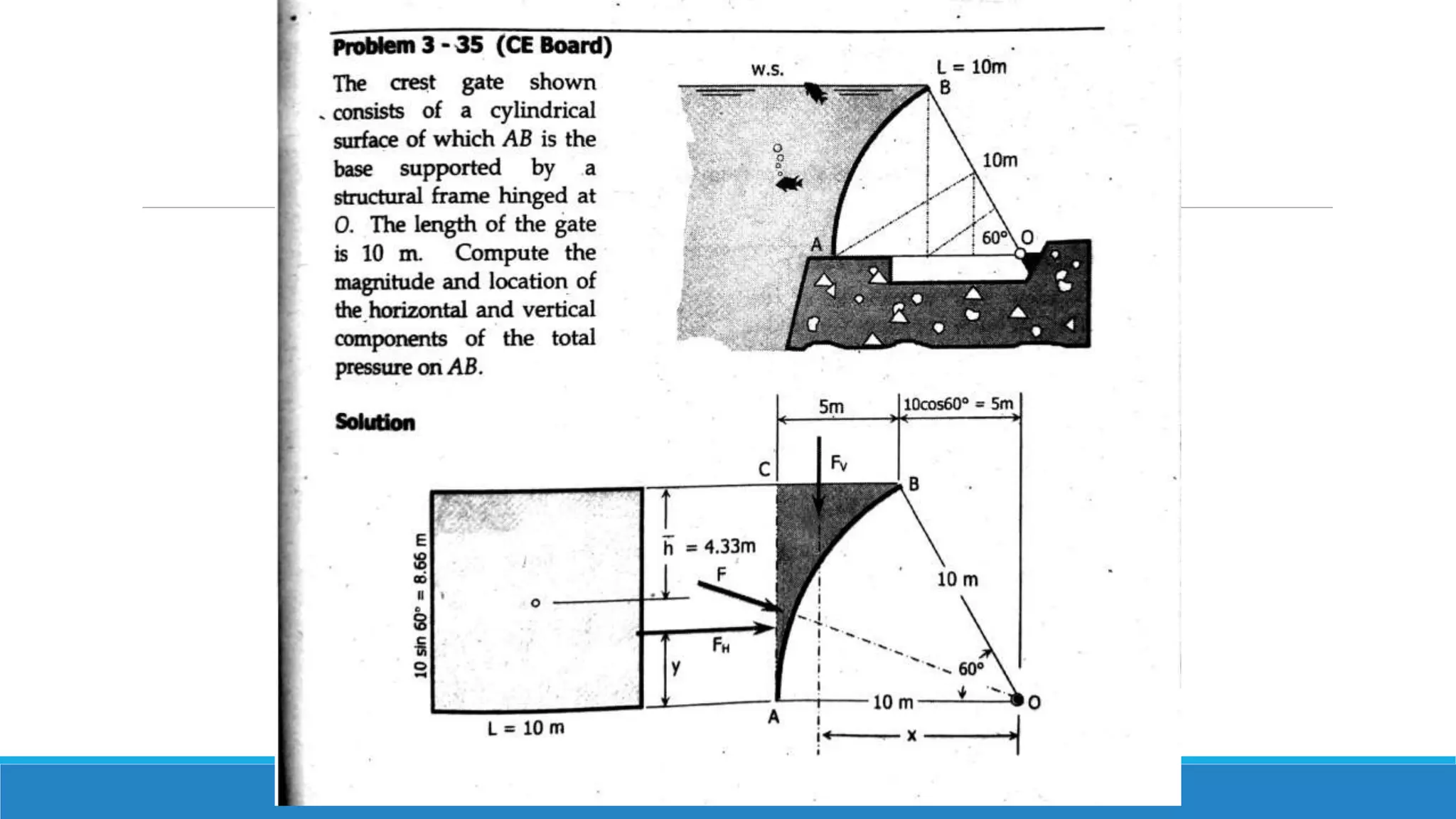
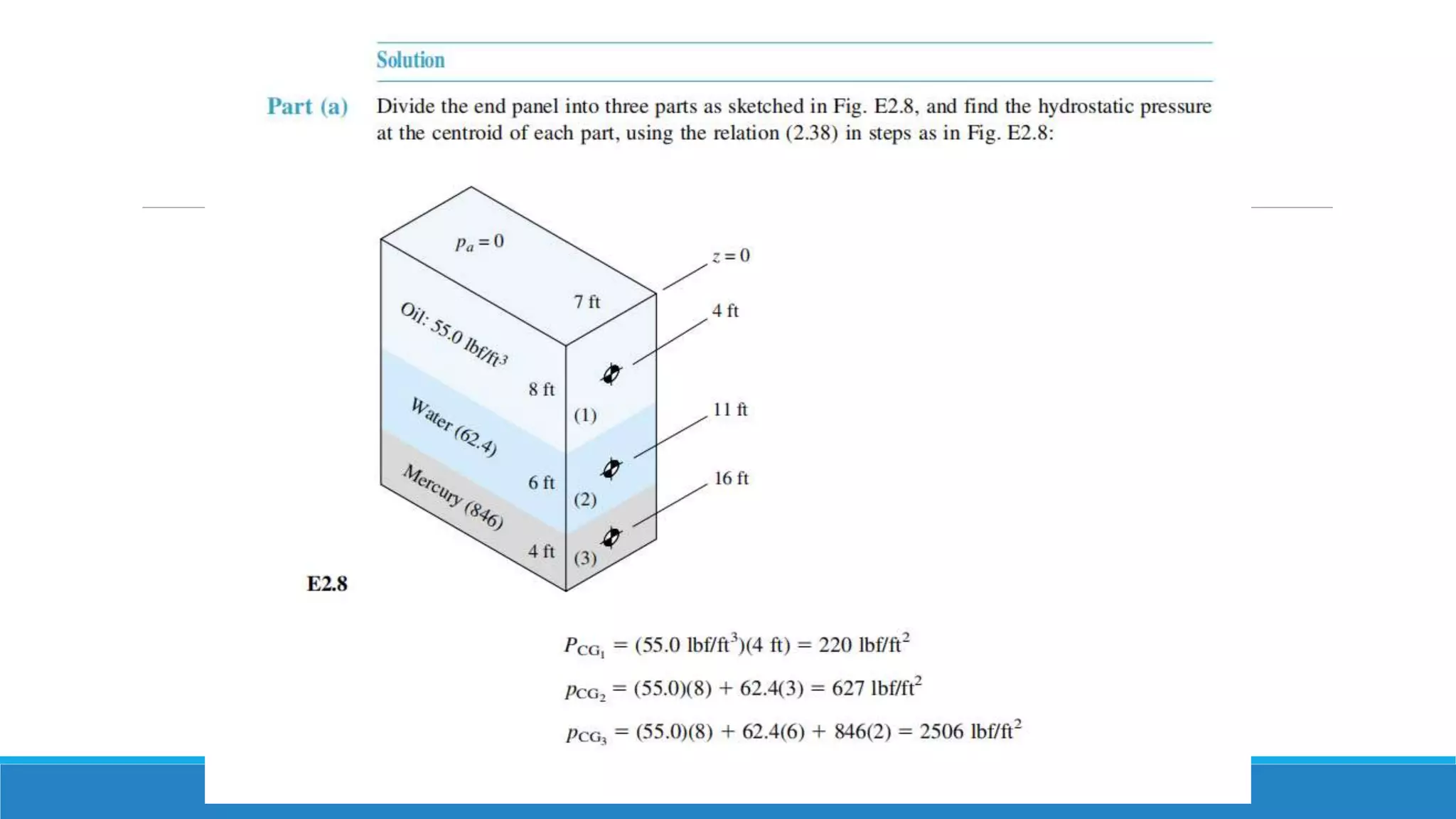
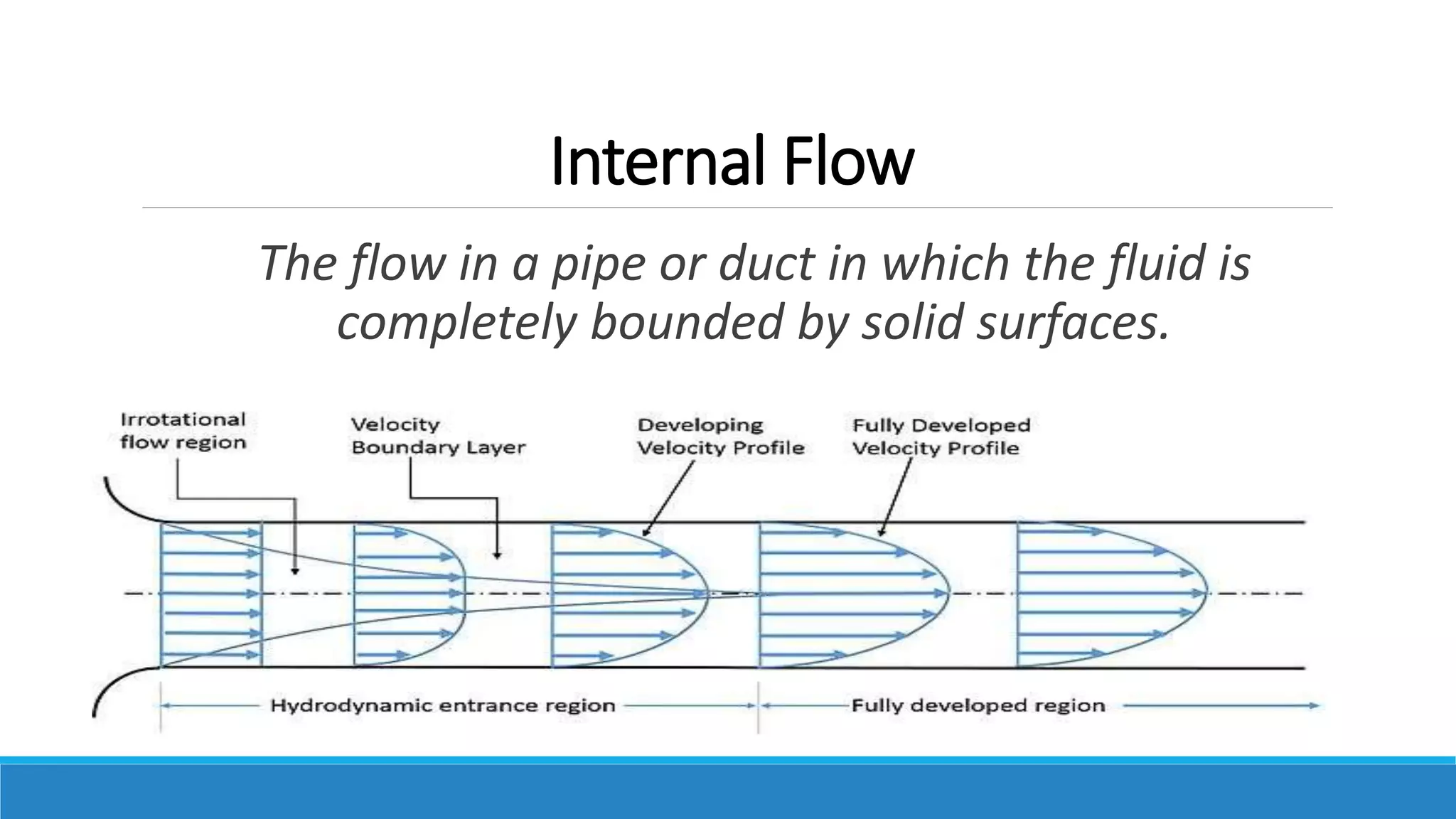
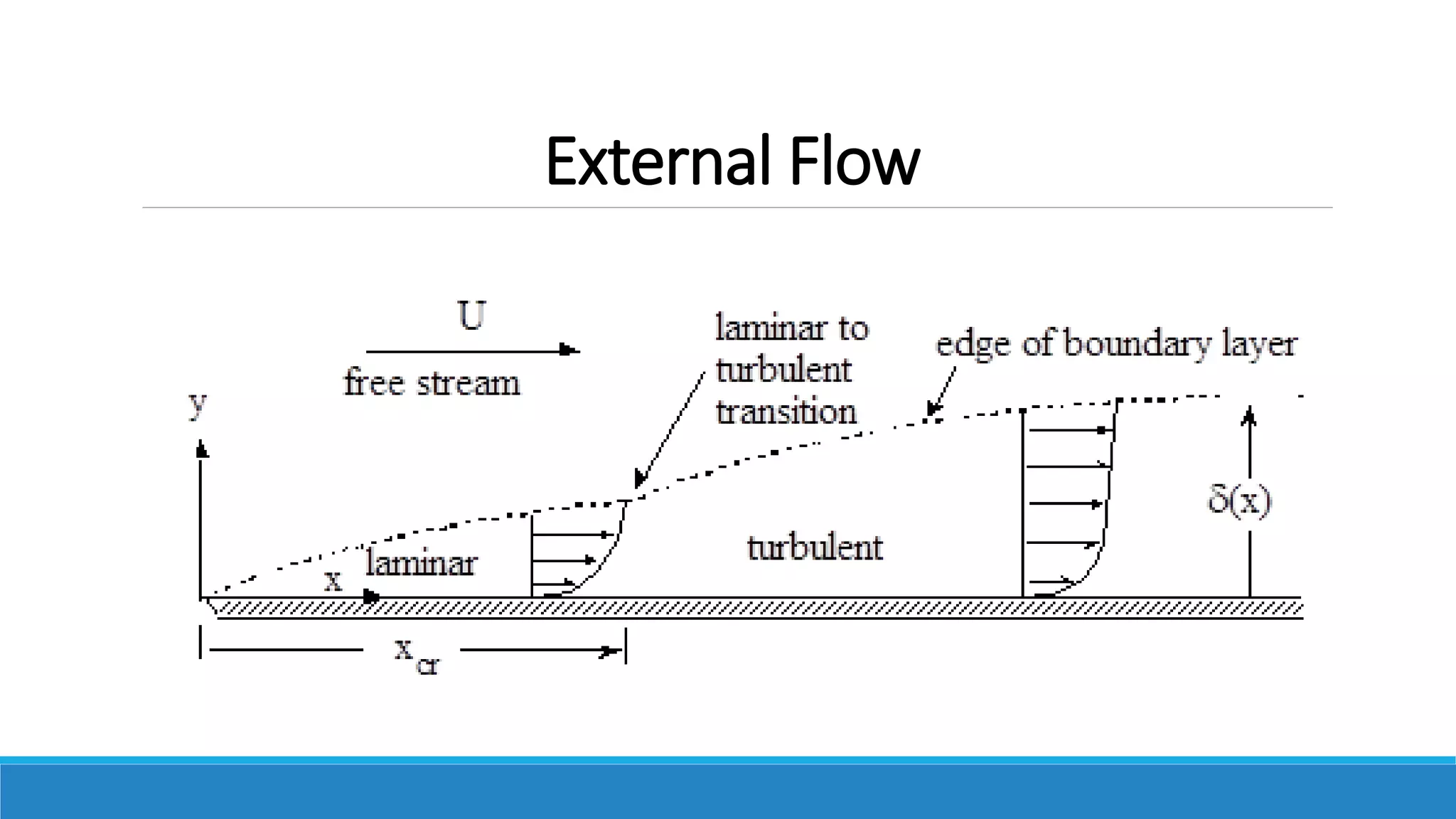
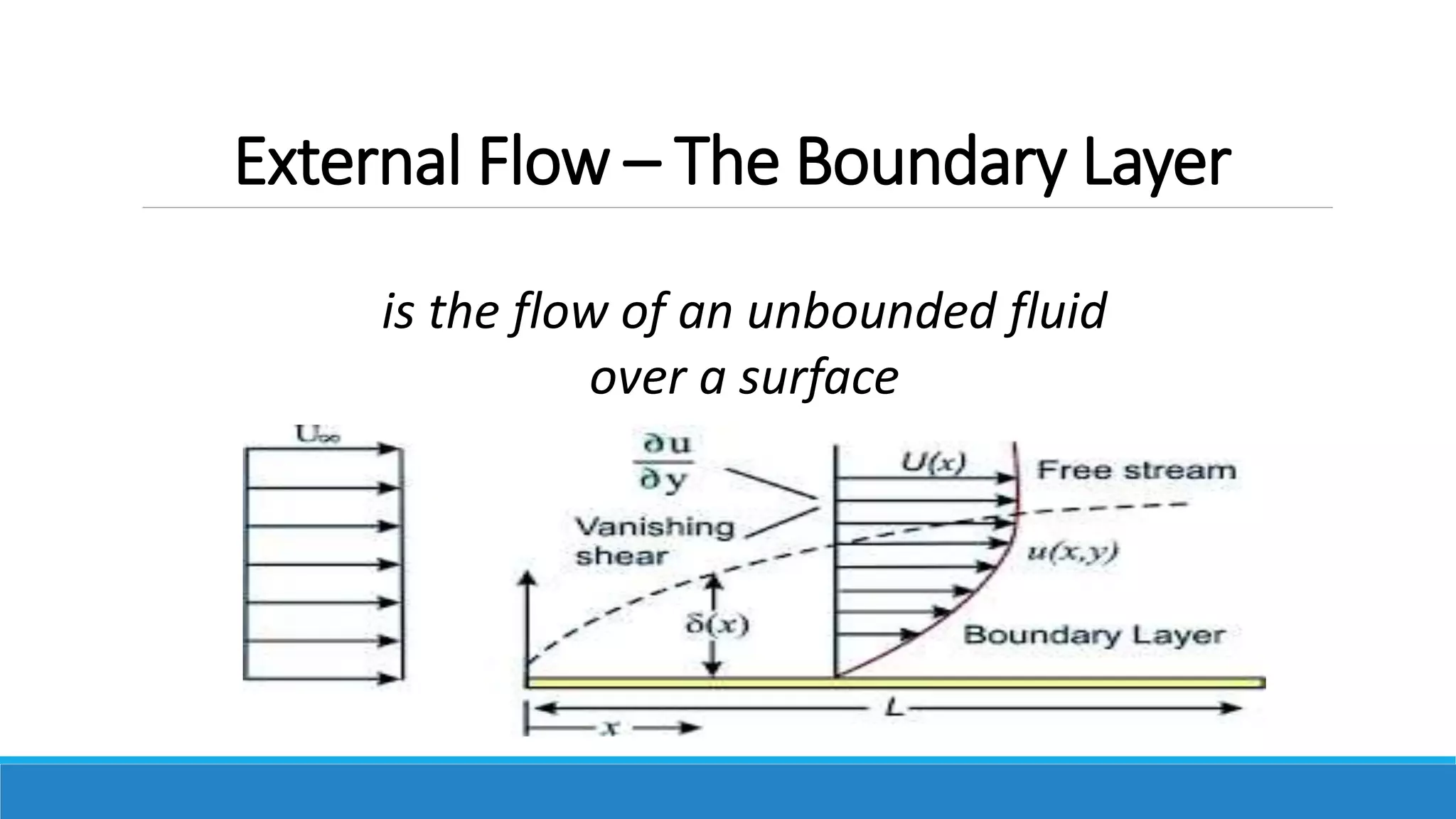
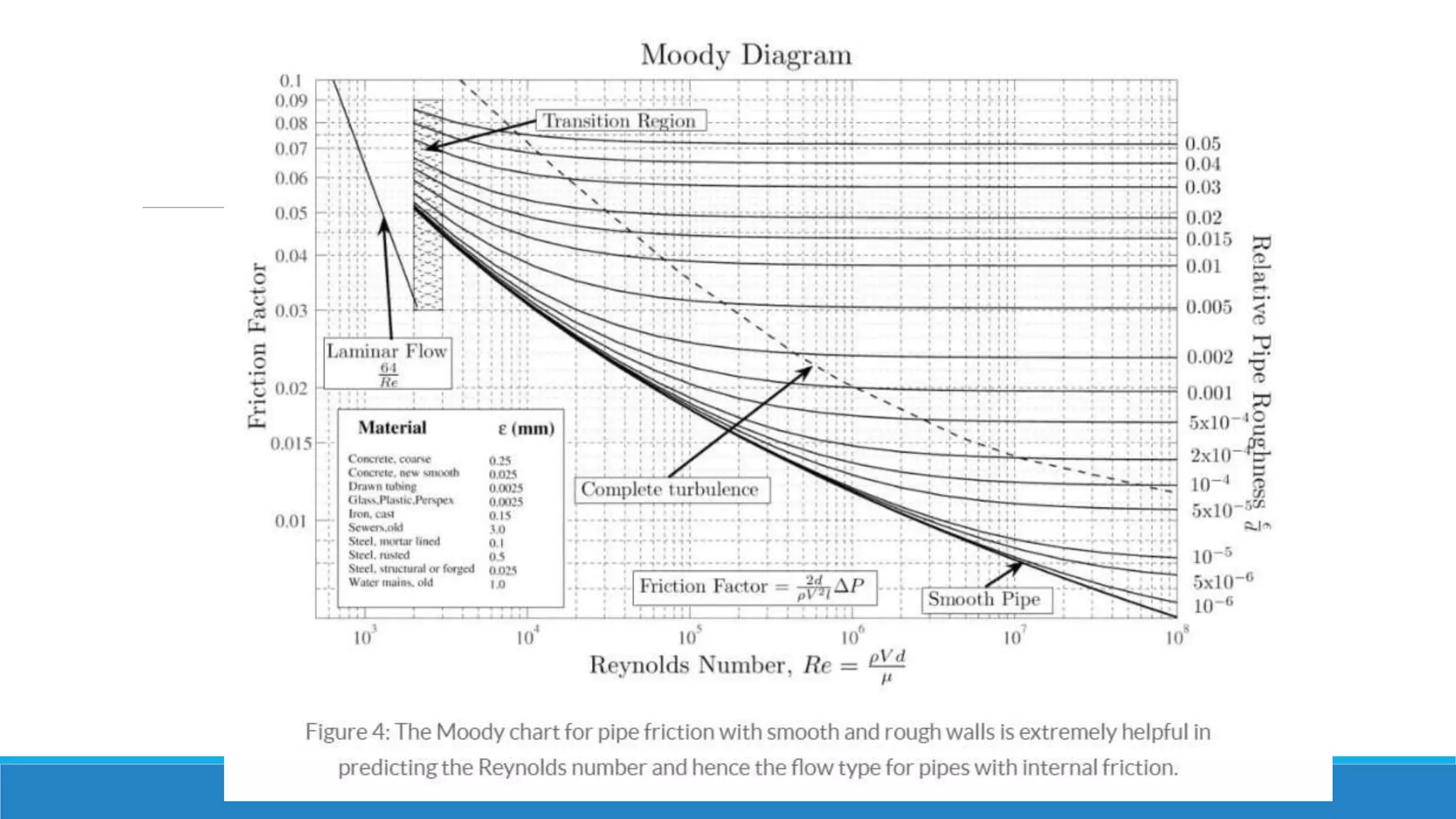
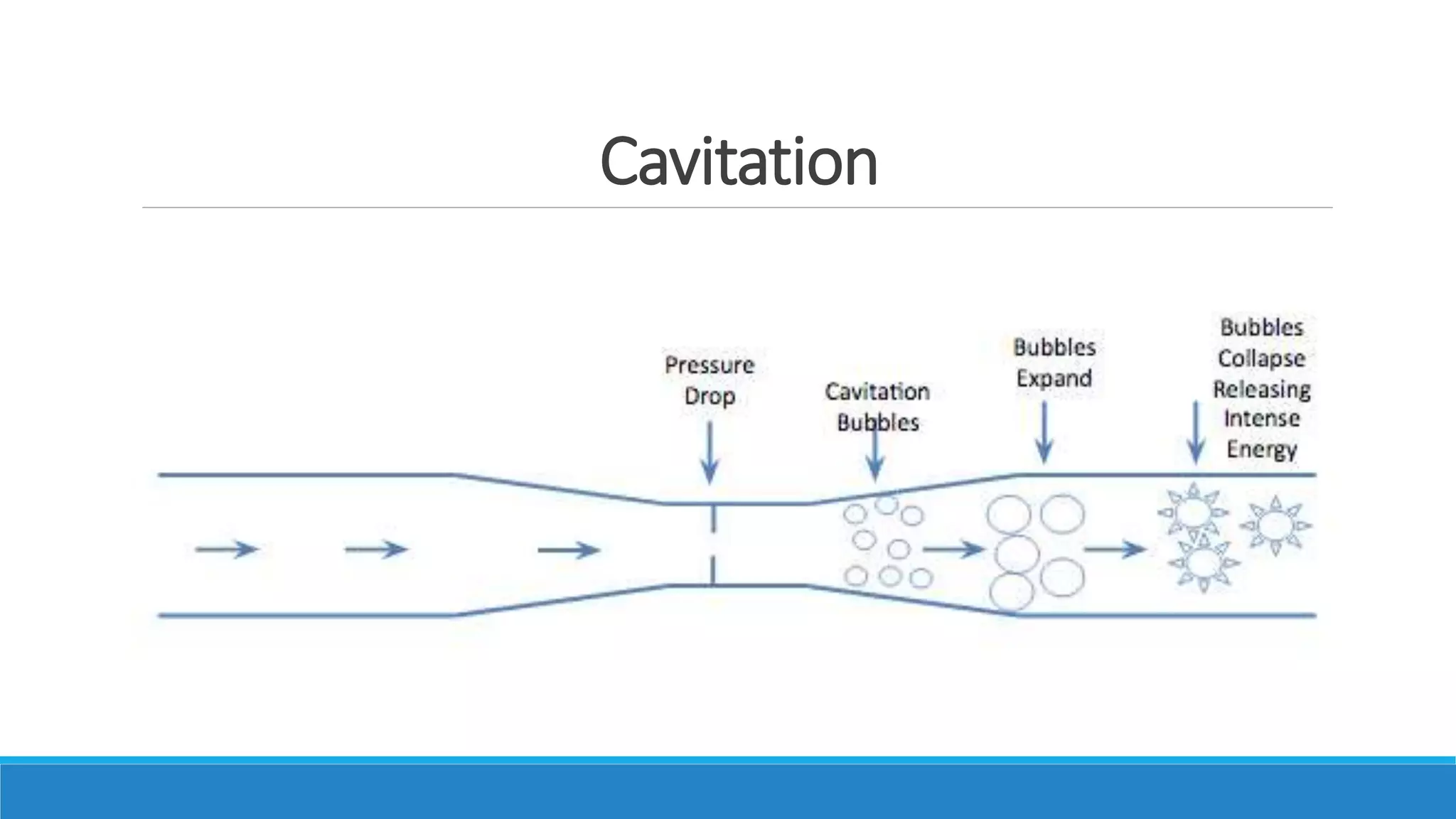
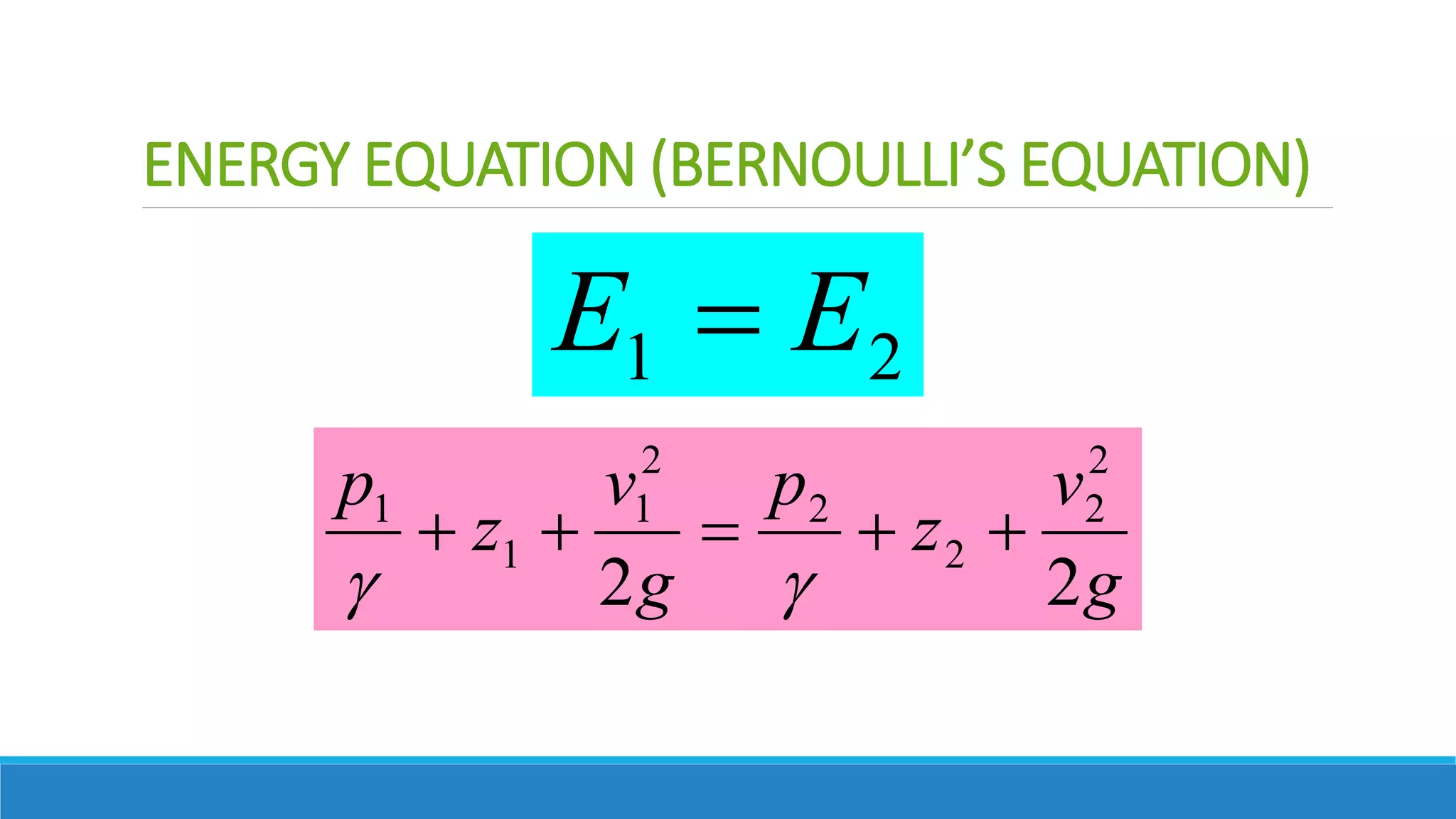This document provides an introduction to fluid mechanics. It defines key terms like fluid, fluid properties, fluid classification, fluid statics, and conservation laws for fluids. Fluid properties discussed include density, viscosity, pressure, and more. Fluid statics topics covered are buoyancy, hydrostatic forces on surfaces. Conservation laws explained are continuity, energy, and momentum equations. Sample problems are provided for concepts like manometry, buoyancy, and hydrostatic forces. Open channel flow is also introduced.