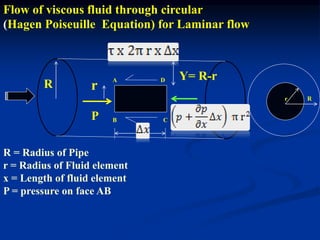
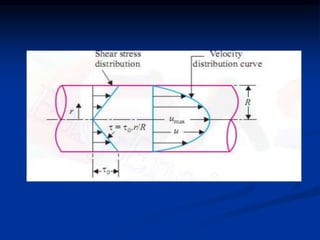
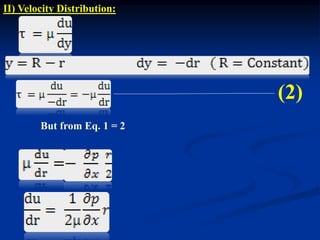
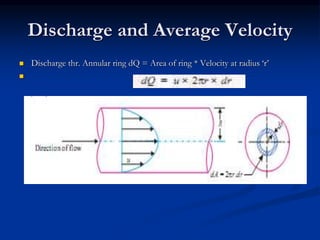
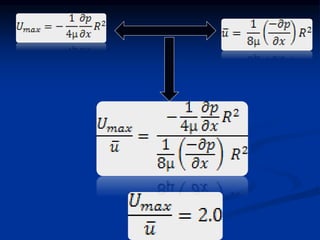
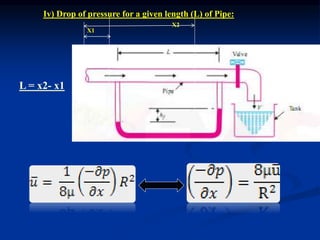
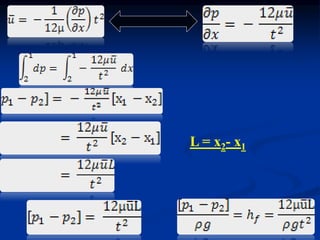
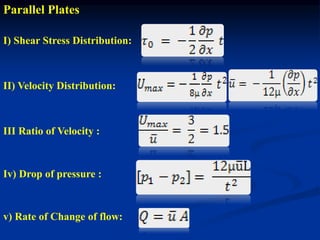
The document discusses fluid dynamics, focusing on the flow of viscous fluids through pipes and between parallel plates, detailing equations such as Hagen-Poiseuille for laminar flow and Darcy-Weisbach for head loss due to friction. It includes various methods for measuring viscosity, including capillary tube and falling sphere resistance methods, along with examples and calculations of pressure drop, shear stress, and average velocity. Additionally, it covers specific problems related to flow rates and pressure gradients for different fluids and pipe configurations.

1. SRES’S SANJIVANI COE, KOPARGAON
Laminar Flow
PREPARED BY
MR. CHAUDHARI. V. S
DEPARTMENT OF CIVIL ENGINEERING

2. Viscous Flow
Section I Section III
Flow of Viscous Fluid
Circular pipe
Two Parallele Pipe
Lose of Head due
Friction
Coefficient of viscosity
- Capillary tube method,
- orifice type
- falling sphere resistance method
- Rotating cylinder method
 Network of pipes (Hardy-cross method)
Section II

3. Section I

4. R
Y= R-r
P
A
B C
D
r
r R
Flow of viscous fluid through circular
(Hagen Poiseuille Equation) for Laminar flow
R = Radius of Pipe
r = Radius of Fluid element
x = Length of fluid element
P = pressure on face AB

5. i) Shear Stress Distribution: Pressure force on fluid elements: ABCD
1) Pressure force on AB =
2) Pressure forec on CD=
3) Shear force on Surface =
No Acceleration & Submission of all forces:
(1)

7. II) Velocity Distribution:
(2)
But from Eq. 1 = 2

8. Integrating w.r.t. “r”
(3)
C = Constant
Value obtaned by bounty
Condition
r = R, u =0
(4)
(5)
(6)

9. Discharge and Average Velocity
 Discharge thr. Annular ring dQ = Area of ring * Velocity at radius ‘r’


10. III Ratio of Maximum Velocity to Average Velocity:

12. X1
X2
L = x2- x1
Iv) Drop of pressure for a given length (L) of Pipe:

13. -
-
Integrating the w.r.t. x
Loss of Pressure Head:
Above eq. (7) is called as
Hagen Poiseuille eq. for
steady uniform laminar flow.
(7)

14. Friction Factor ‘ f ’
 Loss of head due to friction in pipe is expressed
by Darcys-Weisbach Eq.

 ----(8)
 Equate eq. 7 and 8

15. Circular Pipe
(Hagen Poiseuille Equation) for Laminar flow
I) Shear Stress Distribution:
II) Velocity Distribution:
III Ratio of Maximum Velocity to Average Velocity:
Iv) Drop of pressure :

16. Ex 1) A crude oil of viscosity 0.97 poise and relative density 0.9 is
flowing through a horizontal circular pipe of diameter 100 mm
and of length 10 m. Calculate the difference of pressure at the two
ends of the pipe, if 100 kg of the oil is collected in a tank in 30 s.
Assume the laminar flow.
Answer: u =0.471 m/s, p1-p2 = 1462.28 N/m2

17. 2) An oil of viscosity 0.1 Ns/m2 and relative density 0.9 is flowing
through a circular pipe of diameter 50 mm and the length 300 m. the
rate of flow of fluid through the pipe is 3.5 litres/s. Find the pressure
drop in a length of 300 m and also the shear stress at the pipe wall.
1) Pressure Drop
2) Shear Stress
Answer: 1) 684288 N/m2 , 2) 28.512 N/m2

18. 3) A fluid of viscosity 0.7 Ns/m2 and specific gravity 1.3 is flowing
through a circular pipe of diameter 100 mm. The maximum shear
stress at the pipe wall is given as 196.2 N/m2,
find 1) The pressure gradient 2) the average velocity and
3) Reynold number of the flow.
Find
1) The pressure gradient
2) The average velocity and
3) Reynold number of the flow.
Answer: 1) - 7848 N/m2 per m. , 2) u= 3.50 m/s. 3) Re = 650

20. Laminar Flow Between Two Parallel stationary Plates
A
CB
D
t
∆x
Fixed Plate
Fixed Plate
Flow
Direction

21. Pressure force on fluid elements: ABCD
1) Pressure force on AB =
2) Pressure fore on CD=
3) Shear force on Face BC =
3) Shear force on Face AD =
No Acceleration & Submission of all forces:
(1)

22. I) Velocity Distribution:
(2)
Integrating w.r.t.. y
(1)

23. Integrating again
If y=0, u = 0
C2 = 0
If y=t, u = 0

24. II) Ratio of Maximum Velocity to Average Velocity:

26. III) Drop of pressure for a given length (L) of Pipe:
p1 p2
x
Y
x1 L
x2
L = x2- x1

27. L = x2- x1

28. IV) Shear Stress Distribution:
When y=0 or at ‘t’ at the wall of plate
shear stress is max.
Shear stress is zero when y=t/2

29. Parallel Plates
I) Shear Stress Distribution:
II) Velocity Distribution:
III Ratio of Velocity :
Iv) Drop of pressure :
v) Rate of Change of flow:

30. 1) Calculate 1) the pressure gradient along flow 2) the average
velocity and 3) the discharge for an oil of viscosity 0.02 Ns/m2
flowing between two stationary parallel plates 1 m wide maintained
10 mm apart. The velocity midway between the plates is 2 m/s.
i) Pressure Gradient:
ii) Average Velocity:
iii) Discharge:
Answer: 1) - 3200 N/m2 per m , 2) 1.33 m/s 3) 0.0133 m3/s

31. 2) Determine 1) the pressure gradient 2) the shear stress at the two
horizontal parallel plates and 3) the discharge per meter width for
the laminar flow of oil with maximum velocity of 2 m/s between two
horizontal parallel fixed plates which are 100 mm apart. Given
µ = 2.4525 N s/m2
i) Pressure Gradient:
ii) Shear stress:
iii) Discharge:
Answer: 1) - 3924 N/m2 per m , 2) 196.2 N/m2 3) 0.0133 m3/s

32. 3) An oil of viscosity 10 poise flows between two parallel fixed plates
which are kept at a distance of 50 mm apart. Find the rate of oil
between the plates if the drop of pressure in a length of 1.2 m be 0.3
N/cm3. The width of the plates is 200 mm.
Answer: 1) u = 0.52 m/s, 2) Q = 0.0052 m3/s = 5.2 liter/s

33. 4) Water at 15 oC flows between two large parallel plates at distance
of 1.6 mm apart. Determine a) The maximum velocity b) the
pressure drop per unit length and c) The shear stress at the walls of
the average velocity is 0.2 m/s . The viscosity of water at is given as
0.01 poise.
i) Maximum Velocity:
ii) The pressure drop:
iii) Shear Stress:
Answer: 1) 0.3 m/s, 2) 937.44 N/m2 per m 3) 0.749 N/m2

34. 4) The radial clearance between a hydraulic plunger and cylinder
walls is 0.1 mm the length of the plunger is 300 mm and diameter
100 mm. find the velocity of leakage and rate of leakage past the
plunger at an instant when the difference of the pressure between
the two ends of the plunger is 9 m of water . Take µ = 0.0127 poise
Ans: 1) Velocity u = 0.193 m/s 2) Rate of leakage Q = 6.06 x 10 -3
lit/s

35. Section II

36. Lose of Head due Friction:
Loss of Head hf
(Hagen Poiseuille Equation)
Loss of Head due to Fricition hf

37. 1) Water is flowing through a 200mm diameter pipe with coefficient
of friction f = 0.04. The shear stress at a point 40 mm from the pipe
axis is 0.00981 N/cm2. Calculate the shear stress at the pipe wall.
Ans: 1) Re = 400 2) 0.0245 N/ cm2

38. 2) A pipe of diameter 20 cm and length 10000 m is laid at a slope of
1 in 200. An oil of Sp.gr. 0.9 and Viscosity 1.5 poise is pumped up at
the rate of 20 liters per S. Find the head loss due to friction.
Ans: 1) u = 0.6366 m/s 2) Re = 763.89 3) f = 0.02094 4) hf = 86.5 m

39. Section III

40. Coefficient of Viscousity
- Capillary tube method,
- Falling sphere resistance method
- Orifice type Viscometer
- Rotating cylinder method

41.  Capillary Tube Method:
h = Difference of pressure head for length L
D = Diameter of Capillary tube
L = Length of tube
ρ = Density of fluid
µ = Coefficient of viscosity
h
Constant Head Tank
Measuring Tank
L
D

42. Hagen Poiseuilli’s Formula
Head loss
Coefficient of Viscosity

43. Ex 1) The viscosity of an oil of Sp.gr. 0.9 is measured by a capillary
tube of diameter 50 mm. the difference of pressure head between two
points 2 m apart is 0.5 m of water. The mass of oil collected in a
measuring tank is 60 kg in 100 s. Find the viscosity of oil.
Ans: 1) Q = 0.000667 m3/s 2) 0.5075 NS/ m2

44. 2) A capillary tube of diameter 2 mm and length 100 mm is used for
measuring viscosity of a liquid. The difference of pressure between
the two ends of the tube is 0.6867 N/Cm2 and the viscosity of liquid is
0.25 poise. Find the rate of flow of liquid through the tube.
Ans: 1) Q = 107.86 x 10-8 m3/s

45.  Falling Sphere Resistance Method:
L = Distance travelled by sphere in Viscous fluid
t = time taken by Sphere
ρs = Density of Sphere
ρf = Density of fluid
W = Weight of Sphere
Fb= force acting on Sphere
D
Constant Tem.
Bath
Fixed Mark
Sphere
d
U

46. Stoke’s law, Drag Force
Weight of Sphere
Force on Sphere
1
2
3
So 1, 2 & 3

47. 3) A sphere of diameter 2 mm falls 150 mm in 20 s in a viscous liquid.
The density of the sphere is 7500 kg/m3 and of liquid is 900 kg/m3.
Find the co-efficient of viscosity of the liquid.
Ans: 1) 1.917 NS/ m2 or 19.17 poise

48. 4) Find the viscosity of a liquid of sp.gr. 0.8 when a gas bubble of
diameter 10mm rises steadily through the liquid at a velocity 1.2
cm/s. Neglect the weight of the bubble.
rises
Fall
Ans: 1) 3.63 NS/ m2 or 36.3 poise

49.  Orifice Type Viscometer:
Constant Tem.
Bath Oil
Measuring
Cylinder