Mahdi Damghani, profile picture
Uploaded byMahdi Damghani
PPTX, PDF17,265 views

Finite Element Analysis of Truss Structures

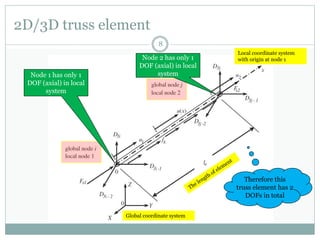
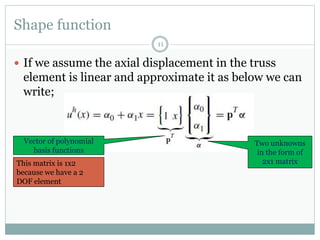
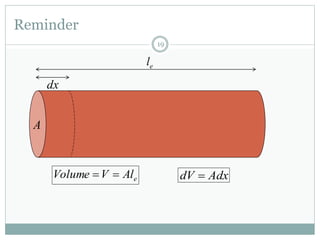
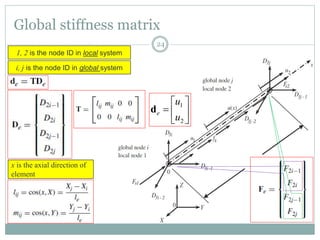
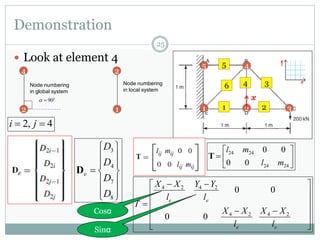
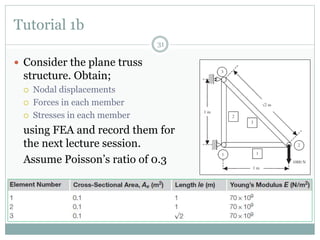
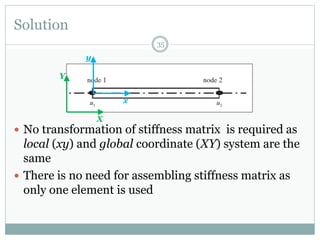
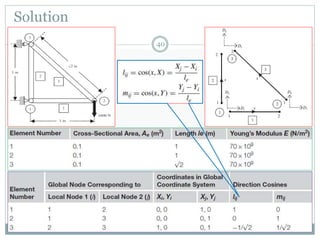
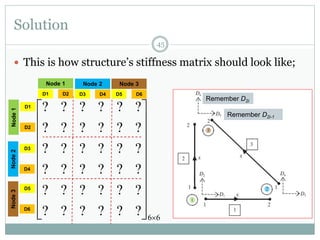
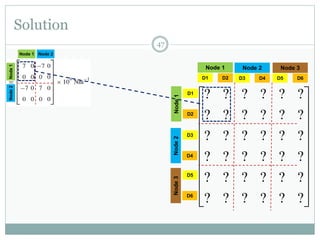
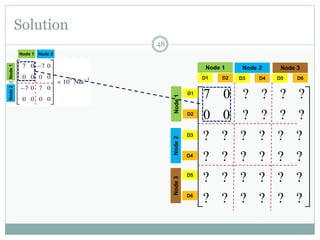
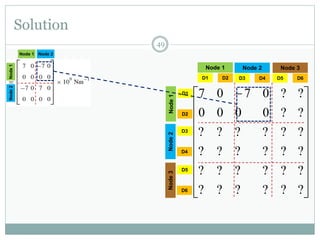
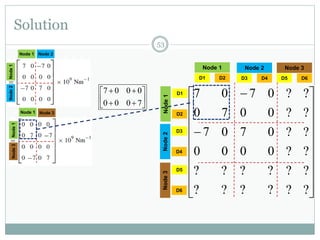
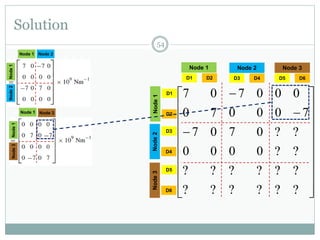
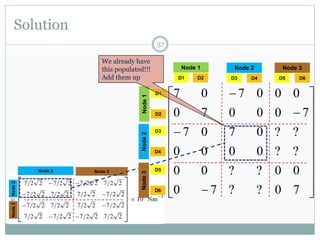
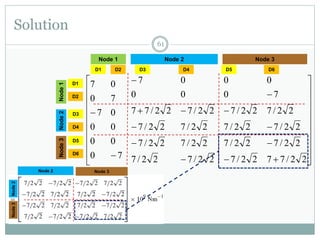
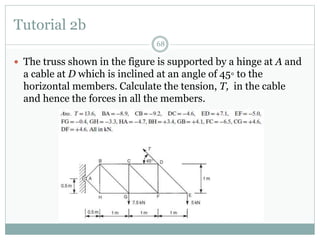
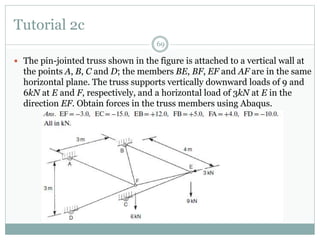
The document discusses the finite element method (FEM) for analyzing truss structures. It begins with objectives of becoming familiar with FEM concepts for truss elements like stiffness matrices and assembling the global stiffness matrix. It then covers derivation of the element stiffness matrix in local coordinates, transforming it to global coordinates, and assembling the global stiffness matrix of the overall structure from the element matrices. Strain and stress calculations are also briefly discussed. Finally, an example problem is presented to demonstrate the FEM process for a simple truss structure.

Embed presentation

Downloaded 501 times
B Y D R . M A H D I D A M G H A N I 2 0 1 6 - 2 0 1 7 Structural Design and Inspection- Finite Element Method (Trusses) 1
Suggested Readings Reference 1 Reference 2 2
Objective(s)  Familiarisation with Finite Element Analysis and Methods (FEA) of truss elements  Familiarity with the concepts of local and global stiffness matrices, strain matrix, shape functions, force matrix, displacement matrix etc  Ability to assemble global stiffness matrix for a truss shape structure  Familiarisation with Finite Element Modelling (FEM) of truss structures using ABAQUS CAE (Tutorial) 3
Introduction 4
Introduction 5 Solar Impulse 2
Introduction  Refer to chapter 6 of Reference 1  Refer to chapter 4 of Reference 2  This method is used in most of commercially available FE based software to solve structural problems  Some typical software in aerospace industry are;  Altair HyperWorks (mostly for optimisation purposes)  MSC Nastran (mostly for linear analysis)  Abaqus (mostly for non-linear analysis)  Ansys (mostly for non-linear analysis) 6
Note 7  Consider a truss structure having a number truss or bar members  Each member can be called as a truss/bar element of a uniform cross section bounded by two nodes, i.e. nd=2
2D/3D truss element 8 Global coordinate system Node 1 has only 1 DOF (axial) in local system Node 2 has only 1 DOF (axial) in local system Therefore this truss element has 2 DOFs in total Local coordinate system with origin at node 1
The Finite Element Analysis (FEA) process 9
Displacement in FEM 10  In finite element methods the displacement for an element is written in the form; e h xxu dN )()(  Approximated displacement within the element Shape function Vectors of displacements at the two nodes of the element This function approximates displacements within the element by just having displacements at the two nodes, i.e. de Question: What should be N(x)???
Shape function 11  If we assume the axial displacement in the truss element is linear and approximate it as below we can write; Two unknowns in the form of 2x1 matrix Vector of polynomial basis functions This matrix is 1x2 because we have a 2 DOF element
Reminder from maths 12  The multiplication of a 1x2 matrix by 2x1 matrix is a 1x1 matrix or a scalar value Matrix21 Matrix12
Reminder from maths 13  Transpose of matrix A is shown as AT
Shape function 14  In order to construct the shape function, boundary conditions must be met; Inverting the matrix
Note 15  How did the following come about?  Reason;     aswritten-rebeCan 0 102 01      eex x lulxu uxu  
Shape function for the truss element 16 We have 2 shape functions because the element has 2 DOFs N1 is contribution of node 1 in the overall displacement of element and is unit at node 1 N2 is contribution of node 2 in the overall displacement of element and is unit at node 2 1)( 1  n i i xN
Note 17  Since the shape functions bring about linear change of displacements within the element, these elements are called Linear Element
Strain calculation 18     ex x Nd  ex LNd  ex Bd          2 1 /1/1 u u ll eex B is called strain matrix L is differential operator
Reminder 19 A el dx eAlVVolume  AdxdV 
Element local stiffness matrix 20 Element stiffness matrix (see chapter 3 of Ref. 2)          e eT ee l l ll /1 /1 /1/1 BB Ec  AdxdV  Aiscrosssectional area Eismodulusof elasticity(material constant)
Elements mass matrix 21  Following similar procedure as stiffness matrix;  Students are advised to familiarise themselves with chapter 3 of ref. 2
Nodal forces 22 Surface force (applied at the node 1) Surface force (applied at the node 2) Body forces (applied between nodes)        2/ 2/ 2 1 exs exs lfF lfF Note that in FEA, body forces are always transferred to the nodes
Global stiffness matrix 23  A structure is comprised of lots of members and each member consists of a set of elements  So far we got stiffness matrix of each element in its local coordinate system  Now the challenge is;  To convert stiffness matrix of each element from local to global coordinate system  Assemble global stiffness matrix of each element into global stiffness of the entire structure
Global stiffness matrix 24 1, 2 is the node ID in local system i, j is the node ID in global system x is the axial direction of element        2 1 u u ed
Demonstration 25  Look at element 4 1 2 3 45 1 2 34 5 6 2 4 Node numbering in global system 1 2 Node numbering in local system o 90 4,2  ji                8 7 4 3 D D D D eD                00 00 2424 2424 ee ee l XX l XX l YY l XX T Cosα Sinα x        2424 2424 00 00 ml ml T
Global stiffness matrix 26
Summary in global system 27  We know for springs;  Using similar concept for truss elements we have (in global system)  KF eee DKF  Node i Node j Node i Node j
Note 28 Node i Node j Node i Node j    jijjijijiijiijij e i jijijjijiijijiij e i DmDmlDmDml l AE F DmlDlDmlDl l AE F 2 2 122 2 122 212 2 212 2 12    
Recover stresses/strain 29  Therefore in FEA, the entire structure is discretised into elements  Displacements at nodes are calculated  Then strains within elements are obtained  Then stresses within elements are obtained    eBdx xx E  
Tutorial 1a 30  follow instructions in “T1a.pdf” document to familiarise yourself with Abaqus CAE.
Tutorial 1b 31  Consider the plane truss structure. Obtain;  Nodal displacements  Forces in each member  Stresses in each member using FEA and record them for the next lecture session. Assume Poisson’s ratio of 0.3
Summary  Element stiffness in local system;  Element stiffness in global system;  Element strains;  Element stresses;  Converting local displacements to global ones; 32          11 11 k e e l AE          2 1 /1/1 u u ll eex  ex Bd
Example 33  Consider a bar of uniform cross-sectional area. The bar is fixed at one end and is subjected to a horizontal load of P at the free end. The dimensions of the bar are shown in the figure, and the bar is made of an isotropic material with Young’s modulus E.
Solution 34  We know that the exact solution for this simple example is:  Now let’s see how Finite Element Method (FEM) deals with such problems Modelling the structure with one element only
Solution 35  No transformation of stiffness matrix is required as local (xy) and global coordinate (XY) system are the same  There is no need for assembling stiffness matrix as only one element is used x y X Y
Solution 36  We do not know F1 , however it is not important as this is on the boundary. What we know is:  Therefore; 1 2 Rows and column of nodes with zero displacement are omitted
Solution 37  Stress in the bar is then calculated as;  This was a very simple example showing the process now let’s look at a more practical and challenging example
Example 38  Consider the plane truss structure. Obtain stresses in each element using FEA.
Solution 39 Element numbers in squares Node numbers in circles As a good practice, use node numbering strategy such as anti- clockwise direction (in this example) as for large problems this saves both computational and memory storage costs. X Y Element local coordinate system Structure global coordinate system In the global system each node has two DOFs (as denoted by Di), whereas in local system each element has only one DOF.
Solution 40
Solution 41  Please note that; θ   sin),cos( cos),cos(   Yxm Xxl ij ij Represents the orientation of each element in relation to global coordinate system
Solution 42  Elements stiffness matrix in global system;  Also note that since we are performing static analysis (not dynamic or vibration analysis) there is no need for mass matrix and therefore we ignore it for this example
Solution 43 el K
Solution 44  So far we have stiffness matrix of each element in global coordinate system  The questions is how to assemble them to get stiffness matrix of the entire structure!!!  Structure has 3 nodes and each node has 2 DOFs, therefore the stiffness matrix of structure should be a 6x6 matrix
Solution 45  This is how structure’s stiffness matrix should look like; 66 ?????? ?????? ?????? ?????? ?????? ??????                      D1 D2 Node 1 D3 D4 Node 2 D5 D6 Node 3 D1 D2 Node1 D3 D4 Node2 D5 D6 Node3 Remember D2i Remember D2i-1
Solution 46                     ?????? ?????? ?????? ?????? ?????? ?????? D1 D2 Node 1 D3 D4 Node 2 D5 D6 Node 3 D1 D2 Node1 D3 D4 Node2 D5 D6 Node3 Node 1 Node 2 Node1Node2 Node 1 Node 3 Node1Node3 Node 2 Node 3 Node2Node3
Solution 47                     ?????? ?????? ?????? ?????? ?????? ?????? D1 D2 Node 1 D3 D4 Node 2 D5 D6 Node 3 D1 D2 Node1 D3 D4 Node2 D5 D6 Node3 Node 1 Node 2 Node1Node2
Solution 48                     ?????? ?????? ?????? ?????? ????00 ????07 D1 D2 Node 1 D3 D4 Node 2 D5 D6 Node 3 D1 D2 Node1 D3 D4 Node2 D5 D6 Node3 Node 1 Node 2 Node1Node2
Solution 49                      ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 0 0 ? ? ? ? 0 7 ? ? ? ? 0 0 ? ? ? ? 0 7 D1 D2 Node 1 D3 D4 Node 2 D5 D6 Node 3 D1 D2 Node1 D3 D4 Node2 D5 D6 Node3 Node 1 Node 2 Node1Node2
Solution 50                       ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 0 0 ? ? ? ? 0 7 ? ? 0 0 0 0 ? ? 0 7 0 7 D1 D2 Node 1 D3 D4 Node 2 D5 D6 Node 3 D1 D2 Node1 D3 D4 Node2 D5 D6 Node 1 Node 2 Node1Node2 Node3
Solution 51                       ? ? ? ? ? ? ? ? ? ? ? ? ? ? 0 0 0 0 ? ? 0 7 0 7 ? ? 0 0 0 0 ? ? 0 7 0 7 D1 D2 Node 1 D3 D4 Node 2 D5 D6 Node 3 D1 D2 Node1 D3 D4 Node2 D5 D6 Node 1 Node 2 Node1Node2 Node3
Solution 52                       ? ? ? ? ? ? ? ? ? ? ? ? ? ? 0 0 0 0 ? ? 0 7 0 7 ? ? 0 0 0 0 ? ? 0 7 0 7 D1 D2 Node 1 D3 D4 Node 2 D5 D6 Node 3 D1 D2 Node1 D3 D4 Node2 D5 D6 Node 1 Node 2 Node1Node2 Node 1 Node 3 Node1Node3 Node3 We already have this populated!!! Add them up
Solution 53                       ? ? ? ? ? ? ? ? ? ? ? ? ? ? 0 0 0 0 ? ? 0 7 0 7 ? ? 0 0 7 0 ? ? 0 7 0 7 D1 D2 Node 1 D3 D4 Node 2 D5 D6 Node 3 D1 D2 Node1 D3 D4 Node2 D5 D6 Node 1 Node 2 Node1Node2 Node 1 Node 3 Node1Node3 Node3           70 00 00 07
Solution 54                        ? ? ? ? 7 0 ? ? ? ? 0 0 ? ? 0 0 0 0 ? ? 0 7 0 7 ? ? 0 0 7 0 ? ? 0 7 0 7 D1 D2 Node 1 D3 D4 Node 2 D5 D6 Node 3 D1 D2 Node1 D3 D4 Node2 D5 Node 1 Node 2 Node1Node2 Node 1 Node 3 Node1Node3 Node3 D6
Solution 55                         ? ? ? ? 7 0 ? ? ? ? 0 0 ? ? 0 0 0 0 ? ? 0 7 0 7 7 0 0 0 7 0 0 0 0 7 0 7 D1 D2 Node 1 D3 D4 Node 2 D5 D6 Node 3 D1 D2 Node1 D3 D4 Node2 D5 Node 1 Node 2 Node1Node2 Node 1 Node 3 Node1Node3 Node3 D6
Solution 56                         7 0 ? ? 7 0 0 0 ? ? 0 0 ? ? 0 0 0 0 ? ? 0 7 0 7 7 0 0 0 7 0 0 0 0 7 0 7 D1 D2 Node 1 D3 D4 Node 2 D5 D6 Node 3 D1 D2 Node1 D3 D4 Node2 D5 Node 1 Node 2 Node1Node2 Node 1 Node 3 Node1Node3 Node3 D6
Solution 57                         7 0 ? ? 7 0 0 0 ? ? 0 0 ? ? 0 0 0 0 ? ? 0 7 0 7 7 0 0 0 7 0 0 0 0 7 0 7 D1 D2 Node 1 D3 D4 Node 2 D5 D6 Node 3 D1 D2 Node1 D3 D4 Node2 D5Node 2 Node 3 Node2Node3 Node3 D6 We already have this populated!!! Add them up
Solution 58                            7 0 ? ? 7 0 0 0 ? ? 0 0 ? ? 22/7 22/7 0 0 ? ? 22/7 22/77 0 7 7 0 0 0 7 0 0 0 0 7 0 7 D1 D2 Node 1 D3 D4 Node 2 D5 D6 Node 3 D1 D2 Node1Node2 Node 2 Node 3 Node2Node3 Node3             22/70 22/70 22/70 22/77 D3 D4 D5 D6
Solution 59                             7 0 22/7 22/7 7 0 0 0 22/7 22/7 0 0 ? ? 22/7 22/7 0 0 ? ? 22/7 22/77 0 7 7 0 0 0 7 0 0 0 0 7 0 7 D1 D2 Node 1 D3 D4 Node 2 D5 D6 Node 3 D1 D2 Node1Node2 Node 2 Node 3 Node2Node3 Node3 D3 D4 D5 D6
Solution 60                                7 0 22/7 22/7 7 0 0 0 22/7 22/7 0 0 22/7 22/7 22/7 22/7 0 0 22/7 22/7 22/7 22/77 0 7 7 0 0 0 7 0 0 0 0 7 0 7 D1 D2 Node 1 D3 D4 Node 2 D5 D6 Node 3 D1 D2 Node1Node2 Node 2 Node 3 Node2Node3 Node3 D3 D4 D5 D6
Solution 61                                   22/77 22/7 22/7 22/7 7 0 22/7 22/7 22/7 22/7 0 0 22/7 22/7 22/7 22/7 0 0 22/7 22/7 22/7 22/77 0 7 7 0 0 0 7 0 0 0 0 7 0 7 D1 D2 Node 1 D3 D4 Node 2 D5 D6 Node 3 D1 D2 Node1Node2 Node 2 Node 3 Node2Node3 Node3 D3 D4 D5 D6
Solution 62  Finally the structure’s stiffness matrix is; 19 10 22/77 22/7 22/7 22/7 7 0 22/7 22/7 22/7 22/7 0 0 22/7 22/7 22/7 22/7 0 0 22/7 22/7 22/7 22/77 0 7 7 0 0 0 7 0 0 0 0 7 0 7                                      NmK
Solution 63 Condensed global matrix
Solution 64            6 4 3 D D D
Solution 65
Note 66  Students are advised to study about second , third and … order elements  What is their difference with first order elements?  How many shape functions do they have?  How does using higher order elements affect the solution time of analysis?
Tutorial 2a 67  Use the FEA to find the magnitude and direction of the deflection of the joint C in the truss. All members have a cross-sectional area of 500mm2 and a Young’s modulus of 200,000 N/mm2.
Tutorial 2b 68  The truss shown in the figure is supported by a hinge at A and a cable at D which is inclined at an angle of 45◦ to the horizontal members. Calculate the tension, T, in the cable and hence the forces in all the members.
Tutorial 2c 69  The pin-jointed truss shown in the figure is attached to a vertical wall at the points A, B, C and D; the members BE, BF, EF and AF are in the same horizontal plane. The truss supports vertically downward loads of 9 and 6kN at E and F, respectively, and a horizontal load of 3kN at E in the direction EF. Obtain forces in the truss members using Abaqus.

More Related Content

PPTX
Lec9 finite element_beam_structures 1
byMahdi Damghani
 
PPT
Finite Element Analysis - UNIT-2
bypropaul
 
PDF
Finite Element Analysis Rajendra M.pdf
byRaviSekhar35
 
PDF
Matrix stiffness method 0910
bymullerasmare
 
PPT
Rayleigh Ritz Method
bySakthivel Murugan
 
PPTX
Truss Analysis using Finite Element method ppt
byanujajape
 
PPTX
Flexibility Energy Method in structural analysis
byMahdi Damghani
 
PPTX
Complimentary Energy Method in structural analysis
byMahdi Damghani
 
Lec9 finite element_beam_structures 1
byMahdi Damghani
 
Finite Element Analysis - UNIT-2
bypropaul
 
Finite Element Analysis Rajendra M.pdf
byRaviSekhar35
 
Matrix stiffness method 0910
bymullerasmare
 
Rayleigh Ritz Method
bySakthivel Murugan
 
Truss Analysis using Finite Element method ppt
byanujajape
 
Flexibility Energy Method in structural analysis
byMahdi Damghani
 
Complimentary Energy Method in structural analysis
byMahdi Damghani
 

What's hot

PPT
Finite element method
bySantosh Chavan
 
PPTX
Introduction to FEA
byKishan Sharma
 
PPTX
Finite Element Analysis - UNIT-5
bypropaul
 
PPTX
Principle of virtual work and unit load method
byMahdi Damghani
 
PPTX
Axisymmetric
byRaj Kumar
 
PPT
Finite Element Analysis - UNIT-1
bypropaul
 
PPT
Constant strain triangular
byrahul183
 
PDF
ME6603 - FINITE ELEMENT ANALYSIS UNIT - I NOTES AND QUESTION BANK
byASHOK KUMAR RAJENDRAN
 
PPT
Introduction to finite element method(fem)
bySreekanth G
 
PDF
Torsion of Non Circular Bars Saint Venants Theory
byDrMathewJohn1
 
PDF
ME6603 - FINITE ELEMENT ANALYSIS UNIT - III NOTES AND QUESTION BANK
byASHOK KUMAR RAJENDRAN
 
PDF
Multiple Degree of Freedom (MDOF) Systems
byMohammad Tawfik
 
PPTX
Lec5-Torsion of thin walled beams
byMahdi Damghani
 
PPT
Endurance limit
byonlinemetallurgy.com
 
PDF
Thin and Thick Cylinders
byDhiraj Bhaskar
 
PPTX
A study on _ buckling
byKishan Sharma
 
PDF
Hydraulic similitude and model analysis
byMohsin Siddique
 
PPTX
Lec3 bending of open and closed sections
byMahdi Damghani
 
PPT
Energy method
byGhassan Alhamdany
 
PPTX
Study of Strain Energy due to Shear, Bending and Torsion
byJay1997Singhania
 
Finite element method
bySantosh Chavan
 
Introduction to FEA
byKishan Sharma
 
Finite Element Analysis - UNIT-5
bypropaul
 
Principle of virtual work and unit load method
byMahdi Damghani
 
Axisymmetric
byRaj Kumar
 
Finite Element Analysis - UNIT-1
bypropaul
 
Constant strain triangular
byrahul183
 
ME6603 - FINITE ELEMENT ANALYSIS UNIT - I NOTES AND QUESTION BANK
byASHOK KUMAR RAJENDRAN
 
Introduction to finite element method(fem)
bySreekanth G
 
Torsion of Non Circular Bars Saint Venants Theory
byDrMathewJohn1
 
ME6603 - FINITE ELEMENT ANALYSIS UNIT - III NOTES AND QUESTION BANK
byASHOK KUMAR RAJENDRAN
 
Multiple Degree of Freedom (MDOF) Systems
byMohammad Tawfik
 
Lec5-Torsion of thin walled beams
byMahdi Damghani
 
Endurance limit
byonlinemetallurgy.com
 
Thin and Thick Cylinders
byDhiraj Bhaskar
 
A study on _ buckling
byKishan Sharma
 
Hydraulic similitude and model analysis
byMohsin Siddique
 
Lec3 bending of open and closed sections
byMahdi Damghani
 
Energy method
byGhassan Alhamdany
 
Study of Strain Energy due to Shear, Bending and Torsion
byJay1997Singhania
 

Viewers also liked

PDF
Introduction to finite element analysis
byTarun Gehlot
 
PPTX
Principle of Virtual Work in structural analysis
byMahdi Damghani
 
PPTX
Finite Element Method
byMuhammad Haris
 
PDF
Finite Element Methode (FEM) Notes
byZulkifli Yunus
 
PPTX
Buckling and tension field beam for aerospace structures
byMahdi Damghani
 
PDF
Finite Element Analysis of the Beams Under Thermal Loading
byMohammad Tawfik
 
PPTX
Fatigue Analysis of Structures (Aerospace Application)
byMahdi Damghani
 
PDF
FEM: Bars and Trusses
byMohammad Tawfik
 
PPTX
Direct integration method
byMahdi Damghani
 
PPT
Analysis of Truss
byDHA Suffa University
 
PDF
FEM: Beams
byMohammad Tawfik
 
PPTX
Slope Deflection Method
byMahdi Damghani
 
PPTX
Trusses and its applications
byMilan Joshi
 
PDF
CONCEPT OF FINITE ELEMENT MODELLING FOR TRUSSES AND BEAMS USING ABAQUS
byIAEME Publication
 
PDF
Manual for the MATLAB program to solve the 2D truss
byMohammaderfan Zandieh
 
PPTX
PPT OF TRUSSES
byAbhishek Mewada
 
Introduction to finite element analysis
byTarun Gehlot
 
Principle of Virtual Work in structural analysis
byMahdi Damghani
 
Finite Element Method
byMuhammad Haris
 
Finite Element Methode (FEM) Notes
byZulkifli Yunus
 
Buckling and tension field beam for aerospace structures
byMahdi Damghani
 
Finite Element Analysis of the Beams Under Thermal Loading
byMohammad Tawfik
 
Fatigue Analysis of Structures (Aerospace Application)
byMahdi Damghani
 
FEM: Bars and Trusses
byMohammad Tawfik
 
Direct integration method
byMahdi Damghani
 
Analysis of Truss
byDHA Suffa University
 
FEM: Beams
byMohammad Tawfik
 
Slope Deflection Method
byMahdi Damghani
 
Trusses and its applications
byMilan Joshi
 
CONCEPT OF FINITE ELEMENT MODELLING FOR TRUSSES AND BEAMS USING ABAQUS
byIAEME Publication
 
Manual for the MATLAB program to solve the 2D truss
byMohammaderfan Zandieh
 
PPT OF TRUSSES
byAbhishek Mewada
 

Similar to Finite Element Analysis of Truss Structures

PDF
Finite Element Analysis Lecture Notes Anna University 2013 Regulation
byNAVEEN UTHANDI
 
PDF
Stiffness Method for structure analysis - Truss
byadninhaerul
 
PDF
Module3 direct stiffness- rajesh sir
bySHAMJITH KM
 
PPT
1 d analysis
byDhruvit Lakhani
 
PPT
lec3 Direct Stiffness Approach for Beams and Frames.ppt
byShaheerRizwan1
 
PPTX
Fem frame
byVIMLESH VERMA
 
PDF
Chapter6 stiffness method
byashish2002319
 
DOCX
Finite element modelling
byDeepak Antil
 
PDF
Module3 direct stiffness- rajesh sir
bySHAMJITH KM
 
PDF
solution for 2D truss1
byMohammaderfan Zandieh
 
PPT
Curso de Analisis por elementos finitos
byEnrique C.
 
PPTX
Lec 4 DSM Steps & Numerical Problems.pptx
byUsama3897
 
PPTX
Week 4 - FE Modelling of trusses_Engineering.pptx
byQasimKhan885498
 
PPTX
materi untuk sarjana teknik FEA mesh.pptx
byaldiasbahatmaka2
 
PPTX
FEM.pptx on enginiiering design and coading
bypandeyjii2424
 
PDF
282165203-Module-1-Introduction-to-FEM.pdf
bySilviViv
 
PPTX
Presentation Matrix Methods final.pptx
byShoaibAhmad922112
 
PPTX
DSM.pptx
byshahzaib601980
 
PDF
Introduction_to_exament_Methods.pdf
byMustafaELALAMI
 
PDF
IRJET- Stress – Strain Field Analysis of Mild Steel Component using Finite El...
byIRJET Journal
 
Finite Element Analysis Lecture Notes Anna University 2013 Regulation
byNAVEEN UTHANDI
 
Stiffness Method for structure analysis - Truss
byadninhaerul
 
Module3 direct stiffness- rajesh sir
bySHAMJITH KM
 
1 d analysis
byDhruvit Lakhani
 
lec3 Direct Stiffness Approach for Beams and Frames.ppt
byShaheerRizwan1
 
Fem frame
byVIMLESH VERMA
 
Chapter6 stiffness method
byashish2002319
 
Finite element modelling
byDeepak Antil
 
Module3 direct stiffness- rajesh sir
bySHAMJITH KM
 
solution for 2D truss1
byMohammaderfan Zandieh
 
Curso de Analisis por elementos finitos
byEnrique C.
 
Lec 4 DSM Steps & Numerical Problems.pptx
byUsama3897
 
Week 4 - FE Modelling of trusses_Engineering.pptx
byQasimKhan885498
 
materi untuk sarjana teknik FEA mesh.pptx
byaldiasbahatmaka2
 
FEM.pptx on enginiiering design and coading
bypandeyjii2424
 
282165203-Module-1-Introduction-to-FEM.pdf
bySilviViv
 
Presentation Matrix Methods final.pptx
byShoaibAhmad922112
 
DSM.pptx
byshahzaib601980
 
Introduction_to_exament_Methods.pdf
byMustafaELALAMI
 
IRJET- Stress – Strain Field Analysis of Mild Steel Component using Finite El...
byIRJET Journal
 

More from Mahdi Damghani

PPTX
FEA good practices presentation
byMahdi Damghani
 
PPTX
Lec10 finite element_beam_structures 2
byMahdi Damghani
 
PPTX
Lec8 buckling v2_1
byMahdi Damghani
 
PPTX
Basic Elasticity
byMahdi Damghani
 
PPTX
Lec4 shear of thin walled beams
byMahdi Damghani
 
PPTX
Lec5 total potential_energy_method
byMahdi Damghani
 
PPTX
Lec5 total potential_energy_method
byMahdi Damghani
 
PPTX
Lec3 principle virtual_work_method
byMahdi Damghani
 
PPTX
Lec5 torsion of thin walled beams
byMahdi Damghani
 
PPTX
Structural idealisation 1-2019
byMahdi Damghani
 
PPTX
Lec3 principle virtual_work_method
byMahdi Damghani
 
PPTX
Lec6-Aircraft structural idealisation 1
byMahdi Damghani
 
PPTX
Composite structures simulation (Abaqus)
byMahdi Damghani
 
PPTX
Lec13 solved example
byMahdi Damghani
 
PPTX
Slope-deflection question
byMahdi Damghani
 
FEA good practices presentation
byMahdi Damghani
 
Lec10 finite element_beam_structures 2
byMahdi Damghani
 
Lec8 buckling v2_1
byMahdi Damghani
 
Basic Elasticity
byMahdi Damghani
 
Lec4 shear of thin walled beams
byMahdi Damghani
 
Lec5 total potential_energy_method
byMahdi Damghani
 
Lec5 total potential_energy_method
byMahdi Damghani
 
Lec3 principle virtual_work_method
byMahdi Damghani
 
Lec5 torsion of thin walled beams
byMahdi Damghani
 
Structural idealisation 1-2019
byMahdi Damghani
 
Lec3 principle virtual_work_method
byMahdi Damghani
 
Lec6-Aircraft structural idealisation 1
byMahdi Damghani
 
Composite structures simulation (Abaqus)
byMahdi Damghani
 
Lec13 solved example
byMahdi Damghani
 
Slope-deflection question
byMahdi Damghani
 

Recently uploaded

PDF
Java Programming core java and basics concepts
byHarish Khodke
 
PDF
DSP_Assignment -1_2026 Laboratory Kolkata
byrezafahim81
 
PDF
graph graph graph theory Graph presentation .pdf
bygeekcooder2020
 
PPTX
1.1 Structure of Materials_Material science.pptx
byDr. Sandip Thorat
 
PDF
Finite Automata With Output - Moore and Mealy Machines definitions and Solved...
byNileshPardeshi28
 
PDF
Deterministic Finite Automata to Regular Expression Conversion.pdf
byNileshPardeshi28
 
PDF
Non-Deterministic Finite Automata (NFA) to Deterministic Finite Automata (DFA...
byNileshPardeshi28
 
PPTX
Biological Oxygen Demand (BOD) Numericals-2026.pptx
byChemical Engineering Dept. NIT Rourkela-769008, Odisha, India
 
PDF
Flexibility Matrix Method of Analysis- Part B
byDr. Nitin Naik
 
PDF
Is Your Team Struggling to Adopt BIM?
byRevit BIM Services
 
PDF
SURAJIT PARAMANIK_ME_3RD_THERMODYNAMICS.pdf
byastikparamanik1970
 
PDF
Learn Linux in your Android Phone (Learn on the Go)
byNarendran Solai Sridharan
 
PDF
algothon event ppt from gdg on campus nsec
byasutoshkumar560
 
PPTX
Operational Amplifier (op - amp), types of op amp
byVaishaliVaishali14
 
PDF
UNIT02_TRE_GEOMETRIC DESIGN.pdf_________
byAaquib Ansari
 
PPTX
Why Precision Matters CO2 N2 Gas Filling Systems Neometrix
byNeometrix_Engineering_Pvt_Ltd
 
PPTX
Power Electronics_PE_lecture_10_presentation .pptx
bykavitabani2
 
PPTX
70,000 RPM Aerospace Bearing Testing – Why High-Speed Validation Is Critical
byNeometrix_Engineering_Pvt_Ltd
 
PPTX
Design and Development of Friction Stir Welding joints of Aluminium and Coppe...
byNareshKumarSingh12
 
PPTX
Hospital Management System Project- 220180107010.pptx
bypravjo279
 
Java Programming core java and basics concepts
byHarish Khodke
 
DSP_Assignment -1_2026 Laboratory Kolkata
byrezafahim81
 
graph graph graph theory Graph presentation .pdf
bygeekcooder2020
 
1.1 Structure of Materials_Material science.pptx
byDr. Sandip Thorat
 
Finite Automata With Output - Moore and Mealy Machines definitions and Solved...
byNileshPardeshi28
 
Deterministic Finite Automata to Regular Expression Conversion.pdf
byNileshPardeshi28
 
Non-Deterministic Finite Automata (NFA) to Deterministic Finite Automata (DFA...
byNileshPardeshi28
 
Biological Oxygen Demand (BOD) Numericals-2026.pptx
byChemical Engineering Dept. NIT Rourkela-769008, Odisha, India
 
Flexibility Matrix Method of Analysis- Part B
byDr. Nitin Naik
 
Is Your Team Struggling to Adopt BIM?
byRevit BIM Services
 
SURAJIT PARAMANIK_ME_3RD_THERMODYNAMICS.pdf
byastikparamanik1970
 
Learn Linux in your Android Phone (Learn on the Go)
byNarendran Solai Sridharan
 
algothon event ppt from gdg on campus nsec
byasutoshkumar560
 
Operational Amplifier (op - amp), types of op amp
byVaishaliVaishali14
 
UNIT02_TRE_GEOMETRIC DESIGN.pdf_________
byAaquib Ansari
 
Why Precision Matters CO2 N2 Gas Filling Systems Neometrix
byNeometrix_Engineering_Pvt_Ltd
 
Power Electronics_PE_lecture_10_presentation .pptx
bykavitabani2
 
70,000 RPM Aerospace Bearing Testing – Why High-Speed Validation Is Critical
byNeometrix_Engineering_Pvt_Ltd
 
Design and Development of Friction Stir Welding joints of Aluminium and Coppe...
byNareshKumarSingh12
 
Hospital Management System Project- 220180107010.pptx
bypravjo279
 

Finite Element Analysis of Truss Structures