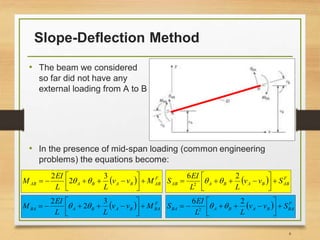
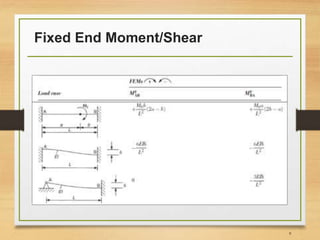
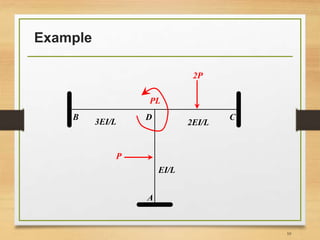
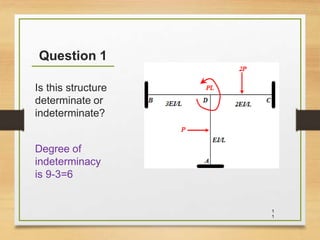
This document provides an example of solving a structural analysis problem using the slope-deflection method. It includes: 1) Introducing the slope-deflection equations for a beam with mid-span loading. 2) Presenting a sample frame structure problem and determining it is indeterminate. 3) Writing the slope-deflection equations and equilibrium equations to solve for member end forces and joint rotations. 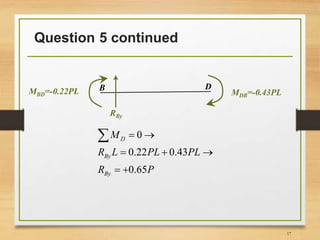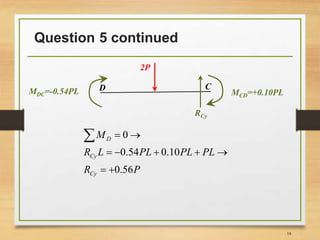4) Calculating support reactions based on the member end forces. 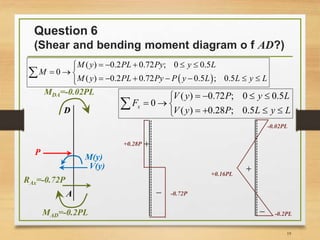5) Drawing the shear and bending moment diagrams.

1. Structural Analysis Example with
Solutions
By
Dr. Mahdi Damghani
2016-2017
1

2. Objective(s)
• Review of structural analysis methods and
procedures learnt in this module
• Preparation for final exam (familiarity with a typical
question) as this year’s exam will be different from
previous years
2

3. Session plan
Introduction
(5-10 mins)
Slope-Deflection
theory by students
(5-10 mins)
Q&A
(5 mins)
Solving a
representative
example (30 mins)
Q&A
(5-10 mins)
3

4. Asking Questions
• Ask in publicly
• Write your questions in the following link and I will
answer them all at the end of the session:
https://padlet.com/mahdi_damghani/SDI
4

5. Topics covered in this module
• Direct integration method
• Macaulay’s method
• Slope-deflection method
• Principle of virtual work
• Rigid bodies
• Deformable bodies
• Unit load method
• Principle of complementary energy
• Castigliano’s second theorem
• Principle of total potential energy
• Castigliano’s first theorem
• Rayleigh-Ritz
• Finite element analysis of truss structures
• Finite element analysis of beam structures
• Finite element analysis of frame structures
5
Objectives satisfied
by the assignment
Assessment in the
final exam
Assessment in the
final exam with all
details

6. Slope-Deflection Method
• The beam we considered
so far did not have any
external loading from A to B
6
• In the presence of mid-span loading (common engineering
problems) the equations become:
  F
ABBABAAB Mvv
LL
EI
M 




3
2
2
   F
ABBABAAB Svv
LL
EI
S 




26
2

  F
BABABABA Mvv
LL
EI
M 




3
2
2
   F
BABABABA Svv
LL
EI
S 




26
2


7. Fixed End Moment/Shear
• MAB
F, MBA
F are fixed end moments at nodes A and B,
respectively.
• Moments at two ends of beam when beam is clamped at
both ends under external loading (see next slides)
• SAB
F, SBA
F are fixed end shears at nodes A and B,
respectively.
• Shears at two ends of beam when beam is clamped at both
ends under external loading (see next slides)
7

8. Fixed End Moment/Shear
8

9. Fixed End Moment/Shear
9

10. Example
10
PL
2P
CDB
A
P
3EI/L 2EI/L
EI/L

11. Question 1
Is this structure
determinate or
indeterminate?
Degree of
indeterminacy
is 9-3=6
1
1

12. Question 2
(slope-deflection equations?)
12
  F
ABBABAAB Mvv
LL
EI
M 




3
2
2

  F
BABABABA Mvv
LL
EI
M 




3
2
2

 
8
2
8
2
2 0 PL
L
EI
M
PL
L
EI
M DADDAAD
A
  
 
 
8
4
8
2
2 0 PL
L
EI
M
PL
L
EI
M DDAADDA
A
  
 
  DBDDBBD
L
EI
M
L
EI
M B
  6
2
32 0
 

 
  DDBBDDB
L
EI
M
L
EI
M B
  12
2
32 0
 

 
 
4
4
8
2
2
22 0 PL
L
EI
M
PL
L
EI
M DCDDCCD
C
 

 
 
 
4
8
8
2
2
22 0 PL
L
EI
M
PL
L
EI
M DDCCDDC
C
 

 
 

13. Question 3
(Equation of equilibrium at joints?)
1313
PL
D
MDB
MDA
MDC
0 PLMMM DCDADB

14. Question 4
(Rotation of joint D?)
14
0 PLMMM DCDADB
8
4 PL
L
EI
M DDA  DDB
L
EI
M 
12

4
8 PL
L
EI
M DDC  
2
7
192
D
PL
EI
 

15. Question 5
(Reaction at support locations?)
15
2
2 2 7
0.2
8 192 8
AD D
EI PL EI PL PL
M PL
L L EI

 
        
 
2
4 4 7
0.02
8 192 8
DA D
EI PL EI PL PL
M PL
L L EI

 
         
 
6
0.22BD D
EI
M PL
L
   
12
0.43DB D
EI
M PL
L
   
4
0.10
4
CD D
EI PL
M PL
L
    
8
0.54
4
DC D
EI PL
M PL
L
    

16. Question 5 continued
16
A
P
EI/L
MAD=-0.2PL
MDA=-0.02PL
D
0
0.02 0.2 0.5
0.72
D
Ax
Ax
M
R L PL PL PL
R P
 
    
 

RAx

17. Question 5 continued
17
B
MDB=-0.43PLMBD=-0.22PL
D
0
0.22 0.43
0.65
D
By
By
M
R L PL PL
R P
 
  
 

RBy

18. Question 5 continued
18
D
MCD=+0.10PLMDC=-0.54PL
C
0
0.54 0.10
0.56
D
Cy
Cy
M
R L PL PL PL
R P
 
    
 

RCy
2P

19. Question 6
(Shear and bending moment diagram o f AD?)
19
A
P
MAD=-0.2PL
MDA=-0.02PL
D
RAx=-0.72P
M(y)
V(y)
( ) 0.72 ; 0 0.5
0
( ) 0.28 ; 0.5
x
V y P y L
F
V y P L y L
   
  
   

 
( ) 0.2 0.72 ; 0 0.5
0
( ) 0.2 0.72 0.5 ; 0.5
M y PL Py y L
M
M y PL Py P y L L y L
    
  
      



-0.72P
+0.28P


-0.2PL
+0.16PL
-0.02PL