This document discusses the direct stiffness method for structural analysis. It begins by introducing the direct stiffness method and its key aspects, including using member stiffness matrices to express actions and displacements at both ends of each member. It then provides examples of applying the direct stiffness method to analyze a plane truss member and plane frame member. This involves deriving the member stiffness matrices in local coordinates, and transforming displacement, load, and stiffness matrices between local and global coordinate systems using rotation matrices.

1. Structural Analysis - III
Di t Stiff M th dDirect Stiffness Method
Dr. Rajesh K. N.
Assistant Professor in Civil EngineeringAssistant Professor in Civil Engineering
Govt. College of Engineering, Kannur
Dept. of CE, GCE Kannur Dr.RajeshKNDept. of CE, GCE Kannur Dr.RajeshKN
1

2. Module IIIModule III
Direct stiffness method
• Introduction – element stiffness matrix – rotation transformation
Direct stiffness method
matrix – transformation of displacement and load vectors and
stiffness matrix – equivalent nodal forces and load vectors –
assembly of stiffness matrix and load vector – determination ofassembly of stiffness matrix and load vector determination of
nodal displacement and element forces – analysis of plane truss
beam and plane frame (with numerical examples) – analysis of
grid space frame (without numerical examples)grid – space frame (without numerical examples)
Dept. of CE, GCE Kannur Dr.RajeshKN
2

3. Introduction
• The formalised stiffness method involves evaluating the
displacement transformation matrix CMJ correctlyp y
• Generation of matrix CMJ is not suitable for computer
programming
H th l ti f di t tiff th d• Hence the evolution of direct stiffness method
Dept. of CE, GCE Kannur Dr.RajeshKN
3

4. Direct stiffness method
• We need to simplify the assembling process of SJ , theJ
assembled structure stiffness matrix
• The key to this is to use member stiffness matrices for actionsThe key to this is to use member stiffness matrices for actions
and displacements at BOTH ends of each member
If b di l d i h f• If member displacements are expressed with reference to
global co-ordinates, the process of assembling SJ can be made
simplesimple
Dept. of CE, GCE Kannur Dr.RajeshKN
4

5. Member oriented axes (local coordinates)
d t t i t d ( l b l di t )and structure oriented axes (global coordinates)
Lδ
x
y
L
Local axes
LδL
Lδ
sinLδ θ
Lδ θ
x
YYYY
cosLδ θ
θ
Global axes yGlobal axesGlobal axes
θ
XXXX
Dept. of CE, GCE Kannur Dr.RajeshKN
Global axes

6. 1. Plane truss member
Stiffness coefficients in local coordinates
1
3
2 4
y
0 0
Degrees of freedom
1
⎛ ⎞
⎜ ⎟
Unit displacement
xEA
L
EA
L
⎜ ⎟
⎝ ⎠corr. to DOF 1
0 0
EA EA⎡ ⎤
−⎢ ⎥
[ ]
0 0
0 0 0 0
0 0
M
L L
S
EA EA
⎢ ⎥
⎢ ⎥
⎢ ⎥
⎢ ⎥
−⎢ ⎥
=
Member stiffness matrix in local
coordinates
Dept. of CE, GCE Kannur Dr.RajeshKN
0 0 0 0
L L
⎢ ⎥
⎢
⎢⎣ ⎦
⎥
⎥

7. Transformation of displacement vector
θ
Displacements in global
22 2 cosU D θ=
p g
coordinates: U1 and U2
Displacements in local
di D d D2D
DY iU D θ
12 2 sinU D θ= − θ
1 11 12 1 2cos sinU U U D Dθ θ= + = −
coordinates: D1 and D2
1DY
11 1 cosU D θ=
21 1 sinU D θ=
2 21 22 1 2sin cosU U U D Dθ θ= + = +
1 1cos sinU Dθ θ−⎧ ⎫ ⎧ ⎫⎡ ⎤
⎧ ⎫ ⎧ ⎫⎡ ⎤
1 1
2 2
cos sin
sin cos
U D
U D
θ θ
θ θ
⎧ ⎫ ⎧ ⎫⎡ ⎤
=⎨ ⎬ ⎨ ⎬⎢ ⎥
⎣ ⎦⎩ ⎭ ⎩ ⎭
X 1 1
2 2
cos sin
sin cos
D U
D U
θ θ
θ θ
⎧ ⎫ ⎧ ⎫⎡ ⎤
∴ =⎨ ⎬ ⎨ ⎬⎢ ⎥−⎣ ⎦⎩ ⎭ ⎩ ⎭
Dept. of CE, GCE Kannur Dr.RajeshKN
{ } [ ]{ }D R U=

8. C id i b th d
⎧ ⎫ ⎧ ⎫
Considering both ends,
1 1
2 2
cos sin 0 0
sin cos 0 0
0 0 i
D U
D U
D U
θ θ
θ θ
θ θ
⎧ ⎫ ⎧ ⎫⎡ ⎤
⎪ ⎪ ⎪ ⎪⎢ ⎥−⎪ ⎪ ⎪ ⎪⎢ ⎥=⎨ ⎬ ⎨ ⎬
⎢ ⎥3 3
4 4
0 0 cos sin
0 0 sin cos
D U
D U
θ θ
θ θ
⎨ ⎬ ⎨ ⎬
⎢ ⎥⎪ ⎪ ⎪ ⎪
⎢ ⎥⎪ ⎪ ⎪ ⎪−⎩ ⎭ ⎣ ⎦ ⎩ ⎭
{ } [ ]{ }LOCAL T GLOBALD R D=
[ ] [ ]R O⎡ ⎤
[ ]
[ ] [ ]
[ ] [ ]T
R O
R
O R
⎡ ⎤
= ⎢ ⎥
⎣ ⎦
Rotation matrix
Dept. of CE, GCE Kannur Dr.RajeshKN

9. Transformation of load vector Actions in global
θ
coordinates:
F1 and F2
22 2 cosF A θ= 1 11 12 1 2cos sinF F F A Aθ θ= + = −
22 2
12 2 sinF A θ= − θ 2A 2 21 22 1 2sin cosF F F A Aθ θ= + = +
Y
11 1 cosF A θ=
21 1 sinF A θ=1A 1 1
2 2
cos sin
sin cos
F A
F A
θ θ
θ θ
−⎧ ⎫ ⎧ ⎫⎡ ⎤
=⎨ ⎬ ⎨ ⎬⎢ ⎥
⎣ ⎦⎩ ⎭ ⎩ ⎭
11 1
1 1cos sinA Fθ θ⎧ ⎫ ⎧ ⎫⎡ ⎤
=⎨ ⎬ ⎨ ⎬⎢ ⎥
X
2 2sin cosA Fθ θ
⎨ ⎬ ⎨ ⎬⎢ ⎥−⎩ ⎭ ⎣ ⎦ ⎩ ⎭
{ } [ ]{ }A R F=
Dept. of CE, GCE Kannur Dr.RajeshKN
{ } [ ]{ }A R F=

10. C id i b th dConsidering both ends,
1 1
2 2
cos sin 0 0
sin cos 0 0
A F
A F
θ θ
θ θ
⎧ ⎫ ⎧ ⎫⎡ ⎤
⎪ ⎪ ⎪ ⎪⎢ ⎥−⎪ ⎪ ⎪ ⎪⎢ ⎥=⎨ ⎬ ⎨ ⎬
3 3
4 4
0 0 cos sin
0 0 sin cos
A F
A F
θ θ
θ θ
⎢ ⎥=⎨ ⎬ ⎨ ⎬
⎢ ⎥⎪ ⎪ ⎪ ⎪
⎢ ⎥⎪ ⎪ ⎪ ⎪−⎩ ⎭ ⎣ ⎦ ⎩ ⎭
{ } [ ]{ }LOCAL T GLOBALi.e., A R A=
Dept. of CE, GCE Kannur Dr.RajeshKN
10

11. Transformation of stiffness matrix
{ } [ ]{ }LOCAL M LOCALA S D=
[ ]{ } [ ][ ]{ }T GLOBAL M T GLOBALR A S R D=
{ } [ ] [ ][ ]{ }
1
GLOBAL T M T GLOBALA R S R D
−
=
[ ]{ } [ ][ ]{ }T GLOBAL M T GLOBAL
[ ] [ ]1 T
R R
−{ } [ ] [ ][ ]{ }GLOBAL T M T GLOBAL
{ } [ ]{ }A S D
[ ] [ ]T TR R=
{ } [ ]{ }GLOBAL MS GLOBALA S D=
[ ] [ ] [ ][ ]
T
MS T M TS R S R=where,
Member stiffness matrix in
global coordinates
Dept. of CE, GCE Kannur Dr.RajeshKN

12. [ ] [ ] [ ][ ]
T
S R S R=
T
⎡ ⎤ ⎡ ⎤ ⎡ ⎤
[ ] [ ] [ ][ ]MS T M TS R S R=
0 0 1 0 1 0 0 0
0 0 0 0 0 0 0 0
T
c s c s
s c s cEA
−⎡ ⎤ ⎡ ⎤ ⎡ ⎤
⎢ ⎥ ⎢ ⎥ ⎢ ⎥− −
⎢ ⎥ ⎢ ⎥ ⎢ ⎥=
⎢ ⎥ ⎢ ⎥ ⎢ ⎥0 0 1 0 1 0 0 0
0 0 0 0 0 0 0 0
c s c sL
s c s c
−⎢ ⎥ ⎢ ⎥ ⎢ ⎥
⎢ ⎥ ⎢ ⎥ ⎢ ⎥
− −⎣ ⎦ ⎣ ⎦ ⎣ ⎦
2 2
c cs c cs⎡ ⎤− −
⎢ ⎥ M b tiff t i2 2
2 2
cs s cs sEA
L c cs c cs
⎢ ⎥
− −⎢ ⎥=
⎢ ⎥− −
⎢ ⎥
Member stiffness matrix
in global coordinates
for a plane truss member
2 2
cs s cs s
⎢ ⎥
− −⎣ ⎦
p
Dept. of CE, GCE Kannur Dr.RajeshKN
12

13. 2. Plane frame member
Stiffness coefficients in local coordinates
2 52
4
5
Degrees of freedom0 0 0 0
EA EA⎡ ⎤
1
3
4
6
Degrees of freedom
3 2 3 2
0 0 0 0
12 6 12 6
0 0
L L
EI EI EI EI
L L L L
⎡ ⎤
−⎢ ⎥
⎢ ⎥
⎢ ⎥−
⎢ ⎥
⎢ ⎥
[ ]
2 2
6 4 6 2
0 0
0 0 0 0
Mi
EI EI EI EI
L L L L
S
EA EA
⎢ ⎥
⎢ ⎥−
⎢ ⎥=
⎢ ⎥
−⎢ ⎥
Member stiffness matrix
in local coordinates
3 2 3 2
0 0 0 0
12 6 12 6
0 0
L L
EI EI EI EI
L L L L
−⎢ ⎥
⎢ ⎥
⎢ ⎥
− − −⎢ ⎥
⎢ ⎥
Dept. of CE, GCE Kannur Dr.RajeshKN
2 2
6 2 6 4
0 0
EI EI EI EI
L L L L
⎢ ⎥
⎢ ⎥−
⎢ ⎥⎣ ⎦

14. Transformation of displacement vector
1 1
2 2
cos sin 0 0 0 0
sin cos 0 0 0 0
D U
D U
θ θ
θ θ
⎧ ⎫ ⎧ ⎫⎡ ⎤
⎪ ⎪ ⎪ ⎪⎢ ⎥−
⎪ ⎪ ⎪ ⎪⎢ ⎥
3 3
4 4
0 0 1 0 0 0
0 0 0 cos sin 0
D U
D Uθ θ
⎪ ⎪ ⎪ ⎪⎢ ⎥
⎪ ⎪ ⎪ ⎪⎢ ⎥
=⎨ ⎬ ⎨ ⎬⎢ ⎥
⎪ ⎪ ⎪ ⎪⎢ ⎥
⎪ ⎪ ⎪ ⎪⎢ ⎥5 5
6 6
0 0 0 sin cos 0
0 0 0 0 0 1
D U
D U
θ θ⎪ ⎪ ⎪ ⎪⎢ ⎥−
⎪ ⎪ ⎪ ⎪⎢ ⎥
⎣ ⎦⎩ ⎭ ⎩ ⎭
{ } [ ]{ }LOCAL T GLOBALD R D=
[ ] [ ]R O⎡ ⎤
{ } [ ]{ }LOCAL T GLOBAL
[ ]
[ ] [ ]
[ ] [ ]T
R O
R
O R
⎡ ⎤
= ⎢ ⎥
⎣ ⎦
Rotation matrix
Dept. of CE, GCE Kannur Dr.RajeshKN

15. Transformation of load vector
{ } [ ]{ }LOCAL T GLOBALA R A={ } [ ]{ }
cos sin 0 0 0 0θ θ⎡ ⎤
⎢ ⎥
[ ]
sin cos 0 0 0 0
0 0 1 0 0 0
R
θ θ⎢ ⎥−
⎢ ⎥
⎢ ⎥
= ⎢ ⎥[ ]
0 0 0 cos sin 0
0 0 0 sin cos 0
TR
θ θ
θ θ
= ⎢ ⎥
⎢ ⎥
⎢ ⎥−
⎢ ⎥
0 0 0 0 0 1
⎢ ⎥
⎣ ⎦
Dept. of CE, GCE Kannur Dr.RajeshKN

16. Transformation of stiffness matrix
{ } [ ]{ }GLOBAL MS GLOBALA S D=
[ ] [ ] [ ][ ]T
MS T M TS R S R= Member stiffness matrix in
global coordinatesglobal coordinates
EA EA⎡ ⎤
0 0 0 0
0 0 0 0
c s
s c
⎡ ⎤
⎢ ⎥−
⎢ ⎥
3 2 3 2
0 0 0 0
12 6 12 6
0 0
EA EA
L L
EI EI EI EI
L L L L
⎡ ⎤
−⎢ ⎥
⎢ ⎥
⎢ ⎥−
⎢ ⎥
⎢ ⎥
[ ]
0 0 1 0 0 0
0 0 0 0
0 0 0 0
T
c s
s c
R
⎢ ⎥
⎢ ⎥
= ⎢ ⎥
⎢ ⎥
⎢ ⎥−
⎢ ⎥
[ ]
2 2
6 4 6 2
0 0
0 0 0 0
M
EI EI EI EI
L L L LS
EA EA
L L
⎢ ⎥
⎢ ⎥−
⎢ ⎥=
⎢ ⎥
−⎢ ⎥
Where,
,
0 0 0 0 0 1
⎢ ⎥
⎣ ⎦
3 2 3 2
12 6 12 6
0 0
6 2 6 4
0 0
L L
EI EI EI EI
L L L L
EI EI EI EI
⎢ ⎥
⎢ ⎥
⎢ ⎥− − −⎢ ⎥
⎢ ⎥
⎢ ⎥
Dept. of CE, GCE Kannur Dr.RajeshKN
2 2
0 0
L L L L
⎢ ⎥−
⎢ ⎥⎣ ⎦

17. Assembling global stiffness matrixg g
Plane truss
2
Force
21
3
31
3
2 4
1
3
Action/displacement components in
local coordinates of members
Dept. of CE, GCE Kannur Dr.RajeshKN

18. 4 4
3
4
3
4
2
6
1 56
2
51
4
3
Action/displacement components in
2
5
6
Action/displacement components in
global coordinates of the structure
Dept. of CE, GCE Kannur Dr.RajeshKN
1 5

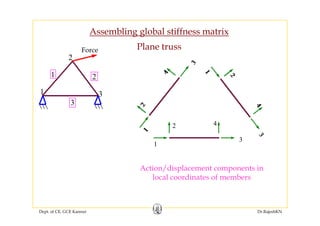
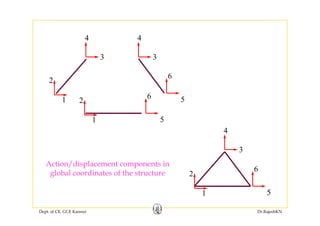
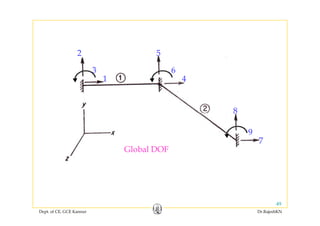
19. 1 2 3 4
Global DOF
11 12 13 14
1 1 1 1
21 22 23 24
2 2
2 2
1
2
M M M M
s s s s
s s s s
c cs c cs
cs s cs sEA
− −⎡ ⎤ ⎡ ⎤
⎢ ⎥ ⎢ ⎥− −
⎢ ⎥ ⎢ ⎥
1 2 3 4
[ ] 1 1 1 1
31 32 33 34
1 1 1 1
41 42 43 44
1 2 2
2 2
2
3
4
M M M M
M M M M
M
s s s s
s s s s
cs s cs sEA
S
c cs c csL
− −
⎢ ⎥ ⎢ ⎥= =
− −⎢ ⎥ ⎢ ⎥
⎢ ⎥ ⎢ ⎥
⎣ ⎦⎣ ⎦
41 42 43 44
1 1 1 1
2 2
4M M M M
s s s scs s cs s
⎢ ⎥ ⎢ ⎥− − ⎣ ⎦⎣ ⎦
1 2 3 4 5 6
1
2
× × × ×⎡ ⎤
⎢ ⎥× × × ×
⎢ ⎥ C t ib ti f
[ ]
2
3
4
JS
× × × ×
⎢ ⎥
× × × ×⎢ ⎥
= ⎢ ⎥
Contribution of
Member 1 to global
stiffness matrix[ ]
4
5
J ⎢ ⎥
× × × ×⎢ ⎥
⎢ ⎥
⎢ ⎥
Dept. of CE, GCE Kannur Dr.RajeshKN
6
⎢ ⎥
⎣ ⎦

20. 3 4 5 6
Global DOF
11 12 13 14
2 2 2 2
21 22 23 24
3
4
M M M M
s s s s
s s s s
⎡ ⎤
⎢ ⎥
⎢ ⎥
3 4 5 6
[ ] 2 2
2
2 2
31 32 33 34
2 2 2 2
41 42 43 44
4
5
6
M M M M
M M M
M
M
s s s s
s s s s
s s s s
S = ⎢ ⎥
⎢ ⎥
⎢ ⎥
⎣ ⎦2 2 2 2
6M M M M
s s s s⎣ ⎦
1 2 3 4 5 6
1
2
⎡ ⎤
⎢ ⎥
⎢ ⎥ C t ib ti f
[ ]
2
3
4
JS
⎢ ⎥
× × × ×⎢ ⎥
= ⎢ ⎥
× × × ×⎢ ⎥
Contribution of
Member 2 to global
stiffness matrix
4
5
6
× × × ×⎢ ⎥
⎢ ⎥× × × ×
⎢ ⎥
⎣ ⎦
Dept. of CE, GCE Kannur Dr.RajeshKN
6
⎢ ⎥
× × × ×⎣ ⎦

21. 11 12 13 14
1⎡ ⎤
1 2 5 6
Global DOF
[ ]
11 12 13 14
3 3 3 3
21 22 23 24
3 3 3 3
1
2
M M M M
M M M M
s s s s
s s s s
S
⎡ ⎤
⎢ ⎥
⎢ ⎥[ ] 3 3
3
3 3
31 32 33 34
3 3 3 3
41 42 43 44
5
6
M M M M
M M M
M
M
s s s s
S = ⎢ ⎥
⎢ ⎥
⎢ ⎥
⎣ ⎦
41 42 43 44
3 3 3 3
6M M M M
s s s s
⎢ ⎥
⎣ ⎦
1 2 3 4 5 6
1
2
× × × ×⎡ ⎤
⎢ ⎥
1 2 3 4 5 6
[ ]
2
3
JS
⎢ ⎥× × × ×
⎢ ⎥
⎢ ⎥
= ⎢ ⎥
Contribution of
Member 3 to global
stiffness matrix[ ]
4
5
JS ⎢ ⎥
⎢ ⎥
⎢ ⎥× × × ×
⎢ ⎥
stiffness matrix
Dept. of CE, GCE Kannur Dr.RajeshKN
6
⎢ ⎥
× × × ×⎣ ⎦

22. Assembled global stiffness matrix
11 12 13 1411 12 13 14
s s s ss s s s+ + 1⎡ ⎤
1 2 3 4 5 6
1 1 1 1
21 22 23 24
1 1 1 1
3 3 3 3
21 22 23 24
3 3 3 3
M M M M
M M M M
M M M M
M M M M
s s s s
s s s s
s s s s
s s s s
+ +
+ +
1
2
⎡ ⎤
⎢ ⎥
⎢ ⎥
⎢ ⎥
[ ]
31 32 3 11 12 13 14
2 2 2 2
21 22 23 24
3 34
1 1 1 1
41 42 43 44
M M M MM M M M
J
s s s s
s s s s
s s s s
s
S
ss s
+ +
=
+ +
3
4
⎢ ⎥
⎢ ⎥
⎢ ⎥
31 3
2 2 2 2
31 32 33
1 1
2
2
1 1
23 3 32
M M M M
M MM M
M M M M
MM
s s
s s s s
s s
s s
s
s s
s
+ +
+
34
2
33 34
3
4
5MM
ss +
⎢ ⎥
⎢ ⎥
⎢ ⎥41 42 43 44
2
41 42 43 44
3 2 23 32 3
6M M M MM M M M
s s s ss s s s+ +
⎢ ⎥
⎣ ⎦
Dept. of CE, GCE Kannur Dr.RajeshKN

23. Imposing boundary conditions 2
p g y
Plane truss example
21
1
2
0U U U U= = = =Boundary conditions are:
3
3
11 2 5 6
0U U U UBoundary conditions are:
{ }GLOBALD
11 12 13 1411 12 13 14
s s s ssF s s s+ +⎧ ⎫ U⎧ ⎫⎡ ⎤
{ }GLOBALD
3 3 3 31 1 1 1
2 21 221 22 23 24
1 1 1 1
23 24
1
2 3 3 3 3
M MM M M M
M M M M
M M
M M M M
s s s s
s s s s
sF
F
s s s
s s s s
+ +
+ +
⎧ ⎫
⎪ ⎪
⎪ ⎪
⎪ ⎪
1
2
U
U
⎧ ⎫⎡ ⎤
⎪ ⎪⎢ ⎥
⎪ ⎪⎢ ⎥
⎪ ⎪⎢ ⎥11 12 13 14
2 2 2 2
21 22 23 24
2
31 32 33 34
1 1 1 1
41 42 43 44
1
3
1 1 1 24 2 2
M M M M M M M
M M M
M
M M M M M
s s s s
s s s
s s s s
s s s s
F
F s
+ +
=
+ +
⎪ ⎪
⎨ ⎬
⎪ ⎪ 4
3
U
U
⎪ ⎪⎢ ⎥
⎨ ⎬⎢ ⎥
⎪ ⎪⎢ ⎥21 1 1 1 24
5
2 2M M MM M M M M
F
F
s
⎪ ⎪
⎪ ⎪
⎪ ⎪
⎩ ⎭
31 32 33 34
2 2 2 2
41 42 43 44
31 32 33 34
3 3 3 3
41 42 43 44
4
5M M M MM M M M
s ss s s s s U
U
+ +
⎪ ⎪⎢ ⎥
⎪ ⎪⎢ ⎥
⎪ ⎪⎢ ⎥
⎣ ⎦⎩ ⎭
Dept. of CE, GCE Kannur Dr.RajeshKN
6
F⎩ ⎭
41 42 43 44
2 2 2 2
41 42 43 44
3 3 3 3 6M MM M M MM M
ss s s s ss s U+ +⎣ ⎦⎩ ⎭

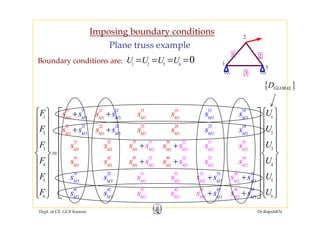
24. Reduced equation systemq y
(after imposing boundary conditions)
33 34
1 1
43 44
11 12
2 2
21 22
3 3MM M M
F U
F U
s ss s+ +⎧ ⎫ ⎧ ⎫⎡ ⎤
=⎨ ⎬ ⎨ ⎬⎢ ⎥+ +⎩ ⎭ ⎣ ⎦⎩ ⎭1 2 1 24 4M MM M
F Us sss⎢ ⎥+ +⎩ ⎭ ⎣ ⎦⎩ ⎭
•This reduced equation system can be solved to get the unknown
displacement components 3 4
,U U
{ } [ ]{ }LOCAL T GLOBALD R D=•From
{ }LOCALD can be found out.
{ } { }D D=F h b
Dept. of CE, GCE Kannur Dr.RajeshKN
{ } { }LOCAL MiD D=•For each member,

25. { } { } [ ]{ }A A S D{ } { } [ ]{ }Mi MLi Mi MiA A S D= +Member end actions
Where,
Fixed end actions on the member,{ }MLiA
Member stiffness matrix,[ ]MiS
[ ]
in local
coordinates
Displacement components of the member,[ ]MiD
{ } { } [ ]{ }LOCAL T GLOBALMi D R DD ==As we know,
{ } { } [ ][ ]{ }i i iM ML M i iT GLOBALA A S R D∴ = +
Dept. of CE, GCE Kannur Dr.RajeshKN
25

26. Direct Stiffness Method: Procedure
STEP 1: Get member stiffness matrices for all members [ ]MiS
STEP 2: Get rotation matrices for all members
[ ]TiR
STEP 3: Transform member stiffness matrices from local coordinates
into global coordinates to get [ ]MSiS[ ]MSi
STEP 4: Assemble global stiffness matrix [ ]JS
STEP 5: Impose boundary conditions to get the reduced stiffness
matrix [ ]S[ ]FFS
Dept. of CE, GCE Kannur Dr.RajeshKN
26

27. STEP 6: Find equivalent joint loads from applied loads on eachq j pp
member (loads other than those applied at joints directly)
STEP 7 T f b ti f l l di t i t l b lSTEP 7: Transform member actions from local coordinates into global
coordinates to get the transformed load vector
STEP 8: Find combined load vector by adding the above
transformed load vector and the loads applied directly at joints
[ ]CA
STEP 9: Find the reduced load vector by removing members in
h l d di b d di i
[ ]FCA
the load vector corresponding to boundary conditions
STEP 10: Get displacement components of the structure in global
coordinates { } [ ] { }
1
F FF FCD S A
−
=
Dept. of CE, GCE Kannur Dr.RajeshKN
27

28. { } [ ]{ }LOCAL T GLOBALD R D=
STEP 11: Get displacement components of each member in local
coordinates
STEP 12: Get member end actions from
{ } { } [ ][ ]{ }Mi MLi Mi iT GLOB iALR DA A S∴ = +
{ } { } [ ][ ]R RC RF FA A S D= − +STEP 13: Get reactions from
{ }RCA represents combined joint loads (actual and
equivalent) applied directly to the supports.q ) pp y pp
Dept. of CE, GCE Kannur Dr.RajeshKN
28

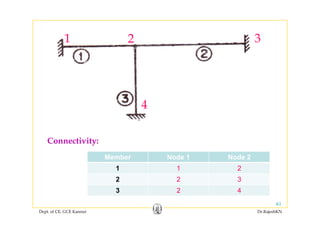
29. • Problem 1:
1 Member stiffness matrices in local co ordinates
1EA ⎡ ⎤⎡ ⎤
1. Member stiffness matrices in local co-ordinates
(without considering restraint DOF)
[ ]1
1
00
1.155
0 0 0 0
M
EA
S L
⎡ ⎤⎡ ⎤
⎢ ⎥⎢ ⎥= =
⎢ ⎥⎢ ⎥
⎣ ⎦ ⎣ ⎦0 0 0 0⎣ ⎦ ⎣ ⎦
[ ]
1 0⎡ ⎤
[ ]
1 2 0⎡ ⎤
Dept. of CE, GCE Kannur Dr.RajeshKN
[ ]2
1 0
0 0
MS
⎡ ⎤
= ⎢ ⎥
⎣ ⎦
[ ]3
1 2 0
0 0MS
⎡ ⎤
= ⎢ ⎥
⎣ ⎦

30. 2. Rotation (transformation) matrices
[ ]1
cos sin 0.5 0.866
i 0 866 0 5
TR
θ θ
θ θ
−⎡ ⎤ ⎡ ⎤
= =⎢ ⎥ ⎢ ⎥
⎣ ⎦ ⎣ ⎦
[ ]1
60 sin cos 0.866 0.5
T
θ θ θ=−
⎢ ⎥ ⎢ ⎥−⎣ ⎦ ⎣ ⎦
[ ]2
90
0 1
1 0
TR
θ
−⎡ ⎤
= ⎢ ⎥
⎣ ⎦90 1 0θ =− ⎣ ⎦
[ ]3
150
0.866 0.5
0.5 0.866
TR
θ =−
− −⎡ ⎤
= ⎢ ⎥−⎣ ⎦⎣ ⎦
Dept. of CE, GCE Kannur Dr.RajeshKN
30

31. 3. Member stiffness matrices in global co-ordinates
(Transformed member stiffness matrices)
[ ] [ ] [ ][ ]1 1 1 1
T
MS T M TS R S R=
0.5 0.866 1 0 0.5 0.8661
0 866 0 5 0 0 0 866 0 51 155
T
− −⎡ ⎤ ⎡ ⎤ ⎡ ⎤
= ⎢ ⎥ ⎢ ⎥ ⎢ ⎥
⎣ ⎦ ⎣ ⎦ ⎣ ⎦0.866 0.5 0 0 0.866 0.51.155⎢ ⎥ ⎢ ⎥ ⎢ ⎥
⎣ ⎦ ⎣ ⎦ ⎣ ⎦
0 216 0 375−⎡ ⎤0.216 0.375
0.375 0.649
−⎡ ⎤
= ⎢ ⎥−⎣ ⎦
Dept. of CE, GCE Kannur Dr.RajeshKN

32. [ ]2
0 1 1 0 0 1
1 0 0 0 1 0
T
MSS
− −⎡ ⎤ ⎡ ⎤ ⎡ ⎤
= ⎢ ⎥ ⎢ ⎥ ⎢ ⎥
⎣ ⎦ ⎣ ⎦ ⎣ ⎦⎣ ⎦ ⎣ ⎦ ⎣ ⎦
0 0⎡ ⎤
= ⎢ ⎥0 1
= ⎢ ⎥
⎣ ⎦
[ ]3
0.866 0.5 1 0 0.866 0.51
0 5 0 866 0 0 0 5 0 8662
T
MSS
− − − −⎡ ⎤ ⎡ ⎤ ⎡ ⎤
= ⎢ ⎥ ⎢ ⎥ ⎢ ⎥
⎣ ⎦ ⎣ ⎦ ⎣ ⎦
[ ]3
0.5 0.866 0 0 0.5 0.8662
MS ⎢ ⎥ ⎢ ⎥ ⎢ ⎥− −⎣ ⎦ ⎣ ⎦ ⎣ ⎦
0.375 0.217⎡ ⎤
⎢ ⎥0.217 0.125
= ⎢ ⎥
⎣ ⎦
Dept. of CE, GCE Kannur Dr.RajeshKN
32

33. 4. Global stiffness matrix
0 216 0 0 375 0 375 0 0 217⎡ ⎤
(by assembling transformed member stiffness matrices)
[ ]
0.216 0 0.375 0.375 0 0.217
0.375 0 0.217 0.649 1 0.125
FFS
+ + − + +⎡ ⎤
= ⎢ ⎥− + + + +⎣ ⎦
0.591 0.158
0 158 1 774
−⎡ ⎤
= ⎢ ⎥
⎣ ⎦0.158 1.774⎢ ⎥−⎣ ⎦
This is the reduced global stiffness matrix, since restraint DOF
were not considered. Hence, boundary conditions are
automatically incorporatedautomatically incorporated.
Dept. of CE, GCE Kannur Dr.RajeshKN

34. 5. Loads
{ }
0
5
FCA
⎧ ⎫
= ⎨ ⎬
−⎩ ⎭
6. Joint displacements6. Joint displacements
0 772⎧ ⎫
{ } [ ] { }
1
F FF FCD S A
−
=
0.772
2.89
−⎧ ⎫
= ⎨ ⎬
−⎩ ⎭
Dept. of CE, GCE Kannur Dr.RajeshKN
34

35. 7. Member forces
{ } { } [ ][ ]{ }Mi MLi Mi iT GLOB iALR DA A S∴ = +
Member 1
{ } { } [ ][ ]{ }
{ } { } [ ][ ]{ }1 1 1 1 1TM M G LM L BAL OR DA A S= + [ ][ ]{ }1 1 1T GLOBALM R DS=
1
0.5 0.8660
1 155
0.772⎡ ⎤ −⎡ ⎤⎢ ⎥= ⎢ ⎥⎢
−⎧
⎥
⎫
⎨ ⎬
1.833
=
⎧ ⎫
⎨ ⎬1.155
0.866 0.5
0 0
2.89⎢ ⎥⎢ ⎥ ⎣ ⎦
⎣ ⎦
⎨ ⎬
−⎩ ⎭ 0
⎨ ⎬
⎩ ⎭
Dept. of CE, GCE Kannur Dr.RajeshKN
35

36. { } [ ][ ]{ }R DA SM b 2 { } [ ][ ]{ }2 2 2 2T GLOBALM M R DA S=Member 2
0.772
2
1 0 0 1
0 0 1 0 .89
−⎡ ⎤ ⎡ ⎤
= ⎢ ⎥ ⎢ ⎥
⎣ ⎦
−⎧ ⎫
⎨
⎦ −⎩⎣
⎬
⎭
2.89
0
⎧
=
⎫
⎨ ⎬
⎩ ⎭
Member 3
{ } [ ][ ]{ }3 3 3 3T GLOBALM M R DA S=
1 2 0 0.866 0.5
0 0 0.5 0.866
0.772
2.89
− −⎡ ⎤ ⎡ ⎤
= ⎢ ⎥ ⎢ ⎥−⎣ ⎦
−⎧ ⎫
⎨
⎣ ⎦
⎬
−⎩ ⎭
1.057
0
=
⎧ ⎫
⎨ ⎬
⎩ ⎭⎣ ⎦ ⎣ ⎦ ⎩ ⎭ ⎩ ⎭
Dept. of CE, GCE Kannur Dr.RajeshKN
36

37. • Problem 2 :
10kN m
5
4
8
4m
0kN m
C
B
20kN 2
4
6
7
94m
1
9
4m 1
2
A EI is constant.
1
2
3
Displacements in
global co-ordinates
Dept. of CE, GCE Kannur Dr.RajeshKN
37
global co ordinates

38. 2 5
6
9 2
1
4
3 6
4
6
2
6
9 2
5
1 1
Ki ti 1Kinematic
indeterminacy
DOF in local co-
ordinates
1
2
33
Dept. of CE, GCE Kannur Dr.RajeshKN
38

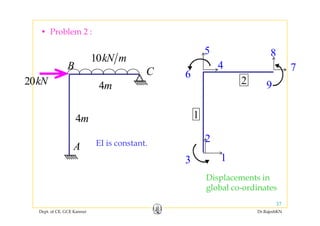
39. 0 0 0 0
12 6 12 6
EA EA
L L
EI EI EI EI
⎡ ⎤
−⎢ ⎥
⎢ ⎥
⎢ ⎥
3 2 3 2
2 2
12 6 12 6
0 0
6 4 6 2
0 0
EI EI EI EI
L L L L
EI EI EI EI
L L L L
⎢ ⎥
⎢ ⎥−
⎢ ⎥
⎢ ⎥
⎢ ⎥−
⎢ ⎥
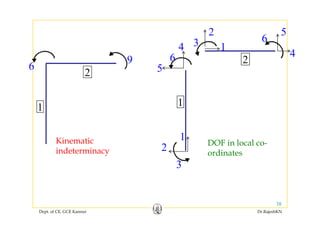
Member stiffness matrix
[ ]
0 0 0 0
12 6 12 6
Mi
L L L LS
EA EA
L L
EI EI EI EI
⎢ ⎥=
⎢ ⎥
−⎢ ⎥
⎢ ⎥
⎢ ⎥
of a 2D frame member in
local coordinates
3 2 3 2
2 2
12 6 12 6
0 0
6 2 6 4
0 0
EI EI EI EI
L L L L
EI EI EI EI
L L L L
⎢ ⎥− − −⎢ ⎥
⎢ ⎥
⎢ ⎥−
⎢ ⎥⎣ ⎦L L L L⎢ ⎥⎣ ⎦
Dept. of CE, GCE Kannur Dr.RajeshKN
39

40. 1. Member stiffness matrices in local co-ordinates
( ith t id i t i t DOF)
6Local DOFMember 1
(without considering restraint DOF)
[ ] 4EI
S ⎡ ⎤=
⎢ ⎥ [ ]1EI EI= =
6Global DOF
[ ]1MS
L
=
⎢ ⎥⎣ ⎦
[ ]1EI EI
Member 2
6 9Global DOF
3 6Local DOF
Member 2
[ ]
4 2EI EI
L LS
⎡ ⎤
⎢ ⎥
⎢ ⎥
6 9Global DOF
0.5EI EI⎡ ⎤
[ ]2
2 4
M
L LS
EI EI
L L
= ⎢ ⎥
⎢ ⎥
⎢ ⎥⎣ ⎦
0.5EI EI
⎡ ⎤
= ⎢ ⎥
⎣ ⎦
Dept. of CE, GCE Kannur Dr.RajeshKN
40

41. 2. Rotation (transformation) matrices
In this case, transformation matrices are:
[ ] [ ]1 1TR = corresponding to local DOF 6
[ ]2
1 0
0 1
TR
⎡ ⎤
= ⎢ ⎥
⎣ ⎦
corresponding to local DOFs 3 & 6
⎣ ⎦
3. Member stiffness matrices in global co-ordinates
(Transformed member stiffness matrices)
[ ]1MSS EI= [ ]2
0.5
0.5
MS
EI EI
S
EI EI
⎡ ⎤
= ⎢ ⎥
⎣ ⎦
Dept. of CE, GCE Kannur Dr.RajeshKN
⎣ ⎦

42. 4 A bl d ( d d d) l b l tiff t i
6 9Gl b l DOF
4. Assembled (and reduced) global stiffness matrix
[ ]
0.5EI EI
S
IE⎡ + ⎤
= ⎢ ⎥
6 9Global DOF
2 0.5
EI
⎡ ⎤
= ⎢ ⎥[ ]
0.5FFS
EI EI
= ⎢ ⎥
⎣ ⎦ 0.5 1
EI= ⎢ ⎥
⎣ ⎦
Dept. of CE, GCE Kannur Dr.RajeshKN

43. 5. Loads
20
13.33 13.33
B
C
20
13.33 20
13.33B
C20
B
20 20
C C20
Fi d d ti A
Combined (Eqlt.+
actual) joint loads
A
Fixed end actions A (Loads in global
co-ordinates)
{ }
13.33
13 33FCA
−⎧ ⎫
= ⎨ ⎬
⎩ ⎭
Loads corresponding to global DOF 6, 9:
Dept. of CE, GCE Kannur Dr.RajeshKN
43
{ }
13.33FC ⎨ ⎬
⎩ ⎭
Loads corresponding to global DOF 6, 9:

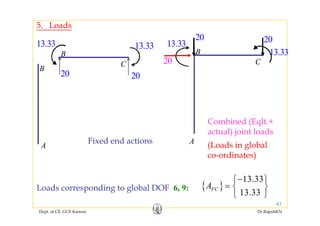
44. 6 Joint displacements
11 431 ⎧ ⎫
6. Joint displacements
{ } [ ] { }
1
F FF FCD S A
−
=
11.43
19.04
1
EI
−⎧
=
⎫
⎨ ⎬
⎩ ⎭
Dept. of CE, GCE Kannur Dr.RajeshKN
44

45. 7. Member end actions
{ } { } [ ][ ]{ }Mi MLi Mi iT GLOB iALR DA A S∴ = +
: fixed end actions for member i{ }MLiA
Member 1
{ } { } [ ][ ]{ }1 1 1 1 1TM M G LM L BAL OR DA A S= +
{ } [ ]{ }DA S { } { }
4 1
0 11 43
EI⎡ ⎤
{ } [ ]{ }1 1 1ML M GLOBALDA S= + { } { }0 11.43
11.43
L EI
⎡ ⎤
= + −⎢ ⎥⎣ ⎦
= −
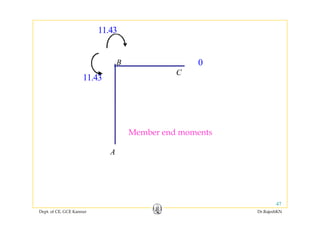
This is the member end action corresponding to local DOF 6
f M b 1 i b d h d f
Dept. of CE, GCE Kannur Dr.RajeshKN
45
of Member 1. i.e., member end moment at the top edge of
Member 1.

46. Member 2
{ } { } [ ]{ }2 2 2 2M ML M GLOBALA A DS= +
Member 2
13.33 11.43
13.33 1
0.5
9.04
1
0.5
EI EI
EI EI EI
−⎧ ⎫ ⎧ ⎫
+
⎡ ⎤
= ⎢ ⎥
⎣
⎨ ⎬ ⎨
−⎩ ⎭ ⎩⎦
⎬
⎭
13.33 1.91−⎧ ⎫ ⎧ ⎫
+⎨ ⎬ ⎨= ⎬
11.42
=
⎧ ⎫
⎨ ⎬
Th th b ti di t l l DOF 3
13.33 13.325
+⎨ ⎬ ⎨
⎩ ⎭
⎬
− ⎩ ⎭ 0
⎨ ⎬
⎩ ⎭
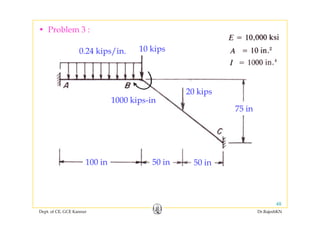
These are the member actions corresponding to local DOFs 3
and 6 of Member 2. i.e., member end moments of Member 2.
Dept. of CE, GCE Kannur Dr.RajeshKN
46

47. 11.43
0B 0B
C
11.43
Member end moments
A
Dept. of CE, GCE Kannur Dr.RajeshKN
47

48. • Problem 3 :
10 kips0.24 kips/in.
20 kips
1000 kips-in
75 in
100 in 50 in 50 in100 in 50 in 50 in
Dept. of CE, GCE Kannur Dr.RajeshKN
48

49. 2 5
1
3
4
6
8
7
9
8
Global DOF
7
Dept. of CE, GCE Kannur Dr.RajeshKN
49

50. 21
3
5
6Local DOF
4
6Local DOF
Dept. of CE, GCE Kannur Dr.RajeshKN
50
4

51. Free DOF
Dept. of CE, GCE Kannur Dr.RajeshKN
51

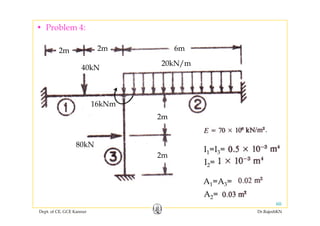
52. 1. Member stiffness matrices in local co-ordinates
( ith t id i t i t DOF)(without considering restraint DOF)
0 0
12 6
XEA
L
EI EI
⎡ ⎤
⎢ ⎥
⎢ ⎥
⎢ ⎥
1000 0 0⎡ ⎤
⎢ ⎥[ ]1 3 2
12 6
0
6 4
0
Z Z
M
Z Z
EI EI
S
L L
EI EI
⎢ ⎥= −
⎢ ⎥
⎢ ⎥
⎢ ⎥−
5
0 120 6000
0 6000 4 10
⎢ ⎥= −
⎢ ⎥
− ×⎢ ⎥⎣ ⎦
2
0
L L
⎢ ⎥−
⎣ ⎦
0 0
12 6
XEA
L
EI EI
⎡ ⎤
⎢ ⎥
⎢ ⎥
⎢ ⎥
800 0 0⎡ ⎤
⎢ ⎥
[ ]2 3 2
12 6
0
6 4
0
Z Z
M
Z Z
EI EI
S
L L
EI EI
⎢ ⎥=
⎢ ⎥
⎢ ⎥
⎢ ⎥
5
0 61.44 3840
0 3840 3.2 10
⎢ ⎥=
⎢ ⎥
×⎢ ⎥⎣ ⎦
Dept. of CE, GCE Kannur Dr.RajeshKN
52
2
0
L L
⎢ ⎥
⎣ ⎦

53. 2. Rotation (transformation) matrices
[ ]
cos sin 0
i 0R
⎡ ⎤
⎢ ⎥
θ θ
θ θ[ ] sin cos 0
0 0 1
TR ⎢ ⎥= −
⎢ ⎥
⎢ ⎥⎣ ⎦
θ θ
Member 1
Member 2
[ ]2
0.8 0.6 0
0.6 0.8 0R
−⎡ ⎤
⎢ ⎥=
⎢ ⎥[ ]1
1 0 0
0 1 0R
⎡ ⎤
⎢ ⎥=
⎢ ⎥
[ ]
0 0 1
⎢ ⎥
⎢ ⎥⎣ ⎦
[ ]1
0 0 1
⎢ ⎥
⎢ ⎥⎣ ⎦
Dept. of CE, GCE Kannur Dr.RajeshKN
53

54. 3. Member stiffness matrices in global co-ordinates
(Transformed member stiffness matrices)
[ ] [ ] [ ][ ]1 1 1 1
T
MS T M TS R S R=
1 0 0 1000 0 0 1 0 0
0 1 0 0 120 6000 0 1 0
T
⎡ ⎤ ⎡ ⎤ ⎡ ⎤
⎢ ⎥ ⎢ ⎥ ⎢ ⎥=
⎢ ⎥ ⎢ ⎥ ⎢ ⎥
5
0 1 0 0 120 6000 0 1 0
0 0 1 0 6000 4 10 0 0 1
= −
⎢ ⎥ ⎢ ⎥ ⎢ ⎥
− ×⎢ ⎥ ⎢ ⎥ ⎢ ⎥⎣ ⎦ ⎣ ⎦ ⎣ ⎦
5
1000 0 0
0 120 6000
⎡ ⎤
⎢ ⎥= −
⎢ ⎥
⎢ ⎥5
0 6000 4 10− ×⎢ ⎥⎣ ⎦
Dept. of CE, GCE Kannur Dr.RajeshKN
54

55. [ ]
0.8 0.6 0 800 0 0 0.8 0.6 0
0 6 0 8 0 0 61 44 3840 0 6 0 8 0
T
S
− −⎡ ⎤ ⎡ ⎤ ⎡ ⎤
⎢ ⎥ ⎢ ⎥ ⎢ ⎥
[ ]2
5
0.6 0.8 0 0 61.44 3840 0.6 0.8 0
0 0 1 0 3840 3.2 10 0 0 1
MSS ⎢ ⎥ ⎢ ⎥ ⎢ ⎥=
⎢ ⎥ ⎢ ⎥ ⎢ ⎥
×⎢ ⎥ ⎢ ⎥ ⎢ ⎥⎣ ⎦ ⎣ ⎦ ⎣ ⎦
0.8 0.6 0 640 480 0
0 6 0 8 0 36 86 49 15 3840
−⎡ ⎤ ⎡ ⎤
⎢ ⎥ ⎢ ⎥= −
⎢ ⎥ ⎢ ⎥
5
0.6 0.8 0 36.86 49.15 3840
0 0 1 2304 3072 3.2 10
= −
⎢ ⎥ ⎢ ⎥
×⎢ ⎥ ⎢ ⎥⎣ ⎦ ⎣ ⎦
534.12 354.51 2304
354 51 327 32 3072
−⎡ ⎤
⎢ ⎥= −
⎢ ⎥
5
354.51 327.32 3072
2304 3072 3.2 10
⎢ ⎥
×⎢ ⎥⎣ ⎦
Dept. of CE, GCE Kannur Dr.RajeshKN

56. 4. Assembled (reduced) global stiffness matrix
1000 534.12 0 354.51 0 2304+ − +⎡ ⎤
. sse b ed ( educed) g oba st ess at x
[ ]
5 5
0 354.51 120 327.32 6000 3072
0 2304 6000 3072 4 10 3.2 10
FFS
⎡ ⎤
⎢ ⎥= − + − +
⎢ ⎥
+ − + × + ×⎢ ⎥⎣ ⎦0 2304 6000 3072 4 10 3.2 10+ + × + ×⎢ ⎥⎣ ⎦
1534 12 354 51 2304⎡ ⎤
5
1534.12 354.51 2304
354.51 447.32 2928
−⎡ ⎤
⎢ ⎥− −
⎢
⎢
=
⎥
⎥5
2304 2928 7.2 10− ×⎢⎣ ⎦⎥
Dept. of CE, GCE Kannur Dr.RajeshKN
56

57. 5. Loads
⎧ ⎫
{ }
0
10JA
⎧ ⎫
⎪ ⎪
= −⎨ ⎬
⎪ ⎪
Actual joint loads
1000⎪ ⎪−⎩ ⎭
{ }
0
22A
⎧ ⎫
⎪ ⎪
⎨ ⎬Equivalent joint loads { } 22
50
EA = −⎨ ⎬
⎪ ⎪−⎩ ⎭
Equivalent joint loads
0⎧ ⎫
⎪ ⎪
{ } { } { } 32
1050
FC J EA A A
⎪ ⎪
= + = −⎨ ⎬
⎪ ⎪−⎩ ⎭
Hence, combined joint loads
Dept. of CE, GCE Kannur Dr.RajeshKN
⎩ ⎭

58. 6. Joint displacements
{ } [ ] { }
1
F FF FCD S A
−
={ } [ ] { }F FF FCD S A
1
{ }
1
1534.12 354.51 2304 0
354.51 447.32 2928 32FD
−
− ⎧ ⎫⎡ ⎤
⎪ ⎪⎢ ⎥∴ = − − −⎨ ⎬⎢ ⎥
⎪ ⎪5
2304 2928 7.2 10 1050
⎢ ⎥
⎪ ⎪− × −⎢ ⎥ ⎩ ⎭⎣ ⎦
0.0206
0.09936
−⎧ ⎫
⎪ ⎪
= −⎨ ⎬0.09936
0.001797
⎨ ⎬
⎪ ⎪−⎩ ⎭
Dept. of CE, GCE Kannur Dr.RajeshKN

59. 7. Member end actions
{ } { } [ ][ ]{ }Mi MLi Mi iT GLOB iALR DA A S∴ = +
1000 0 0 1 0 0 0.0206⎡ ⎤ ⎡ ⎤ −⎧ ⎫
⎪ ⎪
{ }
5
0 120 6000 0 1 0 0.0993
0 6000 4 10 0
6
0 1 0.001797
MLiA
⎡ ⎤ ⎡ ⎤
⎢ ⎥ ⎢ ⎥= + −
⎢ ⎥ ⎢ ⎥
− ×⎢ ⎥ ⎢ ⎥
⎧ ⎫
⎪ ⎪
−⎨
⎣ ⎦ ⎣
⎪
⎩⎦
⎬
⎪− ⎭0 6000 4 10 0 0 1 0.001797⎢ ⎥ ⎢ ⎥⎣ ⎦ ⎣ ⎩⎦ ⎭
8. Reactions
{ } { } [ ][ ]R RC RF FA A S D= − +
Dept. of CE, GCE Kannur Dr.RajeshKN

60. • Problem 4:
20kN/
6m2m2m
40kN
20kN/m
16kNm
2m
80kN
2m
I1=I3=
I2=I2
A1=A3=
Dept. of CE, GCE Kannur Dr.RajeshKN
60
A2=

61. 1 2 31 2 3
4
C ti itConnectivity:
Member Node 1 Node 2
1 1 2
2 2 3
3 2 4
Dept. of CE, GCE Kannur Dr.RajeshKN
61
3 2 4

62. 46
5
46
Free DOF
Dept. of CE, GCE Kannur Dr.RajeshKN
62

63. 1. Member stiffness matrices in local co-ordinates
( ith t id i t i t DOF)(without considering restraint DOF)
5
0 0
3.5 10 0 0
12 6
XEA
L
EI EI
⎡ ⎤
⎢ ⎥
⎡ ⎤×⎢ ⎥
⎢ ⎥⎢ ⎥[ ]1 3 2
12 6
0 0 6562.5 13125
0 13125 35000
6 4
0
Z Z
M
Z Z
EI EI
S
L L
EI EI
⎢ ⎥⎢ ⎥= − = −⎢ ⎥⎢ ⎥
⎢ ⎥−⎢ ⎥ ⎣ ⎦
⎢ ⎥− 2
0
L L
⎢ ⎥
⎣ ⎦
⎡ ⎤
[ ]
5
0 0
3.5 10 0 0
12 6
X
Z Z
EA
L
EI EI
⎡ ⎤
⎢ ⎥
⎡ ⎤×⎢ ⎥
⎢ ⎥⎢ ⎥[ ]2 3 2
2
12 6
0 0 3888.89 11666.67
0 11666.67 46666.67
6 4
0
Z Z
M
Z Z
EI EI
S
L L
EI EI
⎢ ⎥⎢ ⎥= = ⎢ ⎥⎢ ⎥
⎢ ⎥⎢ ⎥ ⎣ ⎦
⎢ ⎥
⎣ ⎦
Dept. of CE, GCE Kannur Dr.RajeshKN
63
2
L L
⎢ ⎥
⎣ ⎦

64. ⎡ ⎤
[ ]
5
0 0
3.5 10 0 0
12 6
0 0 6 62 1312
X
Z Z
EA
L
EI EI
S
⎡ ⎤
⎢ ⎥
⎡ ⎤×⎢ ⎥
⎢ ⎥⎢ ⎥[ ]3 3 2
2
12 6
0 0 6562.5 13125
0 13125 35000
6 4
0
Z Z
M
Z Z
EI EI
S
L L
EI EI
⎢ ⎥⎢ ⎥= = ⎢ ⎥⎢ ⎥
⎢ ⎥⎢ ⎥ ⎣ ⎦
⎢ ⎥
⎣ ⎦
2
L L
⎢ ⎥
⎣ ⎦
Dept. of CE, GCE Kannur Dr.RajeshKN
64

65. 2. Rotation (transformation) matrices
0 1 0−⎡ ⎤1 0 0⎡ ⎤
1 0 0⎡ ⎤
[ ]3
90
0 1 0
1 0 0
0 0 1
R
θ =−
⎡ ⎤
⎢ ⎥=
⎢ ⎥
⎢ ⎥⎣ ⎦
[ ]1
0
1 0 0
0 1 0
0 0 1
R
θ =
⎡ ⎤
⎢ ⎥=
⎢ ⎥
⎢ ⎥⎣ ⎦
[ ]2
0
0 1 0
0 0 1
R
θ =
⎡ ⎤
⎢ ⎥=
⎢ ⎥
⎢ ⎥⎣ ⎦
Member 1
0 0 1⎢ ⎥⎣ ⎦
Member 2
0 0 1⎢ ⎥⎣ ⎦
Member 3
⎣ ⎦
Dept. of CE, GCE Kannur Dr.RajeshKN
65

66. 3. Member stiffness matrices in global co-ordinates
(Transformed member stiffness matrices)
[ ] [ ] [ ][ ]1 1 1 1
T
MS T M TS R S R=
5
3.5 10 0 0
0 6562.5 13125
⎡ ⎤×
⎢ ⎥
= −⎢ ⎥
0 13125 35000
⎢ ⎥
⎢ ⎥−⎣ ⎦
Dept. of CE, GCE Kannur Dr.RajeshKN
66

67. 5T
⎡ ⎤⎡ ⎤ ⎡ ⎤
[ ]
5
2
1 0 0 3.5 10 0 0 1 0 0
0 1 0 0 3888.89 11666.67 0 1 0
T
MSS
⎡ ⎤×⎡ ⎤ ⎡ ⎤
⎢ ⎥⎢ ⎥ ⎢ ⎥= ⎢ ⎥⎢ ⎥ ⎢ ⎥
⎢ ⎥⎢ ⎥ ⎢ ⎥0 0 1 0 11666.67 46666.67 0 0 1⎢ ⎥⎢ ⎥ ⎢ ⎥⎣ ⎦ ⎣ ⎦⎣ ⎦
5
3.5 10 0 0
0 3888.89 11666.67
⎡ ⎤×
⎢ ⎥
= ⎢ ⎥
0 11666.67 46666.67
⎢ ⎥
⎢ ⎥
⎣ ⎦
Dept. of CE, GCE Kannur Dr.RajeshKN
67

68. [ ]
5
3
0 1 0 3.5 10 0 0 0 1 0
1 0 0 0 6562.5 13125 1 0 0
T
MSS
⎡ ⎤− × −⎡ ⎤ ⎡ ⎤
⎢ ⎥⎢ ⎥ ⎢ ⎥= ⎢ ⎥⎢ ⎥ ⎢ ⎥
0 0 1 0 13125 35000 0 0 1
⎢ ⎥⎢ ⎥ ⎢ ⎥
⎢ ⎥⎢ ⎥ ⎢ ⎥⎣ ⎦ ⎣ ⎦⎣ ⎦
5
0 1 0 0 3.5 10 0
1 0 0 6562 5 0 13125
⎡ ⎤− ×⎡ ⎤
⎢ ⎥⎢ ⎥
⎢ ⎥1 0 0 6562.5 0 13125
0 0 1 13125 0 35000
⎢ ⎥⎢ ⎥= − ⎢ ⎥⎢ ⎥
⎢ ⎥⎢ ⎥⎣ ⎦ ⎣ ⎦
6562.5 0 13125⎡ ⎤
⎢ ⎥5
0 3.5 10 0
13125 0 35000
⎢ ⎥= ×
⎢ ⎥
⎢ ⎥⎣ ⎦
Dept. of CE, GCE Kannur Dr.RajeshKN
68
⎣ ⎦

69. 4. Assembled (and reduced) global stiffness matrix. sse b ed (a d educed) g oba st ess at x
5 5
3.5 10 3.5 10 6562.5 0 0 0 0 0 13125⎡ ⎤× + × + + + + +
⎢ ⎥
[ ] 5
0 0 0 6562.5 3888.89 3.5 10 13125 11666.67 0
0 0 13125 13125 11666.67 0 35000 46666.67 35000
FFS
⎢ ⎥
= + + + + × − + +⎢ ⎥
⎢ ⎥+ + − + + + +⎣ ⎦
706562 5 0 13125⎡ ⎤706562.5 0 13125
0 360451.39 1458.33
⎡ ⎤
⎢ ⎥= −
⎢ ⎥
13125 1458.33 116666.67
⎢ ⎥
−⎢ ⎥⎣ ⎦
Dept. of CE, GCE Kannur Dr.RajeshKN

70. 60
5. Loads
20
20 kNm 60 60
2020
60
60
40
4040
40
Fixed end actions
Dept. of CE, GCE Kannur Dr.RajeshKN
7040
Fixed end actions

71. 80kN
0+16=16 kNm0 16 16 kNm
40kN
Combined (equivalent + actual) joint loads
Dept. of CE, GCE Kannur Dr.RajeshKN
71
( q ) j

72. 0⎧ ⎫ 0⎧ ⎫ 0⎧ ⎫
0⎧ ⎫
⎪ ⎪0
0
0
⎧ ⎫
⎪ ⎪
⎪ ⎪
⎪ ⎪
0
20
20
⎧ ⎫
⎪ ⎪−
⎪ ⎪
−⎪ ⎪
0
20
20
⎧ ⎫
⎪ ⎪−
⎪ ⎪
−⎪ ⎪
20
20
0
⎪ ⎪−
⎪ ⎪
−⎪ ⎪
⎪ ⎪
0
0
⎪ ⎪
⎪ ⎪
⎪ ⎪
⎪ ⎪
⎪ ⎪
40
80
⎪ ⎪
⎪ ⎪
⎪ ⎪
⎪ ⎪−
⎪ ⎪
40
80
⎪ ⎪
⎪ ⎪
⎪ ⎪
⎪ ⎪−
⎪ ⎪
{ }
0
60
60
RCA
⎪ ⎪
⎪ ⎪⎪ ⎪
= −⎨ ⎬
⎪ ⎪
⎪ ⎪
{ }
16
;
0
0
JA
⎪ ⎪
−⎪ ⎪
= ⎨ ⎬
⎪ ⎪
⎪ ⎪
{ }
0
;
0
60
EA
⎪ ⎪
⎪ ⎪
= ⎨ ⎬
⎪ ⎪
⎪ ⎪−
{ } { } { }
16
;
0
60
C J EA A A
⎪ ⎪
−⎪ ⎪
= + = ⎨ ⎬
⎪ ⎪
⎪ ⎪−
40
80
⎪ ⎪
⎪ ⎪
⎪ ⎪−
⎪ ⎪
⎪ ⎪
0
0
0
⎪ ⎪
⎪ ⎪
⎪ ⎪
⎪ ⎪
⎪ ⎪
60
60
40
⎪ ⎪
⎪ ⎪
⎪ ⎪
⎪ ⎪
⎪ ⎪
40⎧ ⎫
⎪ ⎪
60
60
40
⎪ ⎪
⎪ ⎪
⎪ ⎪
⎪ ⎪
⎪ ⎪
40⎪ ⎪−⎩ ⎭
80
0
⎪ ⎪
−⎪ ⎪
⎪ ⎪
⎩ ⎭
0
40
⎪ ⎪
⎪ ⎪
⎪ ⎪−⎩ ⎭
{ } 80
16
FCA
⎪ ⎪
= −⎨ ⎬
⎪ ⎪−⎩ ⎭
80
40
⎪ ⎪
−⎪ ⎪
⎪ ⎪−⎩ ⎭
Dept. of CE, GCE Kannur Dr.RajeshKN
72

73. [ ] [ ] { }
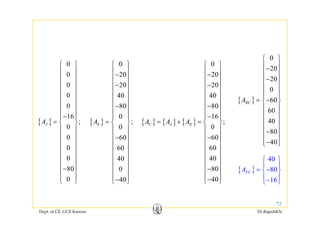
1
D S A
−
=6. Joint displacements
1
706562.5 0 13125 40
−
⎡ ⎤ ⎧ ⎫
⎪ ⎪
[ ] [ ] { }F FF FCD S A=6. Jo t d sp ace e ts
0 360451.39 1458.33 80
13125 1458.33 116666.67 16
⎡ ⎤ ⎧ ⎫
⎪ ⎪⎢ ⎥= − −⎨ ⎬⎢ ⎥
⎪ ⎪− −⎢ ⎥⎣ ⎦ ⎩ ⎭⎢ ⎥⎣ ⎦ ⎩ ⎭
5 9 6
0.142 10 0.646 10 0.160 10 40
− − −
⎡ ⎤× − × − × ⎧ ⎫
⎢ ⎥9 5 7
6 7 5
40
0.646 10 0.277 10 0.348 10 80
160 160 10 0 348 10 0 859 10
− − −
− − −
⎡ ⎤ ⎧ ⎫
⎢ ⎥ ⎪ ⎪
= − × × × −⎨ ⎬⎢ ⎥
⎪ ⎪⎢ ⎥ −× × × ⎩ ⎭⎣ ⎦
160.160 10 0.348 10 0.859 10⎢ ⎥− × × × ⎩ ⎭⎣ ⎦
4
0.594 10−
⎧ ⎫×
⎪ ⎪3
3
0.222 10
0.147 10
−
−
⎪ ⎪
= − ×⎨ ⎬
⎪ ⎪− ×⎩ ⎭
Dept. of CE, GCE Kannur Dr.RajeshKN
73
⎩ ⎭

74. 7. Member end actions
{ } { } [ ][ ]{ }Mi MLi Mi iT GLOB iALR DA A S∴ = +
Dept. of CE, GCE Kannur Dr.RajeshKN

75. Summary
Direct stiffness method
Summary
• Introduction – element stiffness matrix – rotation transformation
matrix – transformation of displacement and load vectors and
stiffness matrix – equivalent nodal forces and load vectors –
assembly of stiffness matrix and load vector – determination ofassembly of stiffness matrix and load vector determination of
nodal displacement and element forces – analysis of plane truss
beam and plane frame (with numerical examples) – analysis of
grid space frame (without numerical examples)grid – space frame (without numerical examples)
Dept. of CE, GCE Kannur Dr.RajeshKN
75

76. • Problem X:
2
6
1 3
5
6
4
5
Dept. of CE, GCE Kannur Dr.RajeshKN
76

77. 0 0
EA EA⎡ ⎤
[ ]1
0 0
1 0 1 0
0 0 0 0 0 0 0 01
M
L L
S
⎡ ⎤
−⎢ ⎥ −⎡ ⎤
⎢ ⎥ ⎢ ⎥
⎢ ⎥ ⎢ ⎥= =
⎢ ⎥ ⎢ ⎥
[ ]1
1 0 1 02
0 0
0 0 0 0
0 0 0 0
M
EA EA
L L
⎢ ⎥ −⎢ ⎥
−⎢ ⎥ ⎢ ⎥
⎣ ⎦⎢ ⎥
⎢ ⎥⎣ ⎦0 0 0 0⎢ ⎥⎣ ⎦
[ ] [ ] [ ]2 3 4S S S= = =[ ] [ ] [ ]2 3 4M M MS S S
1 0 1 0
0 0 0 01
−⎡ ⎤
⎢ ⎥
⎢ ⎥
1 0 1 0
0 0 0 01
−⎡ ⎤
⎢ ⎥
⎢ ⎥[ ]5
0 0 0 01
1 0 1 02.83
0 0 0 0
MS ⎢ ⎥=
−⎢ ⎥
⎢ ⎥
⎣ ⎦
[ ]6
0 0 0 01
1 0 1 02.83
0 0 0 0
MS ⎢ ⎥=
−⎢ ⎥
⎢ ⎥
⎣ ⎦
Dept. of CE, GCE Kannur Dr.RajeshKN
77
⎣ ⎦ ⎣ ⎦

78. Rotation matrices
cos sin 0 0 0 1 0 0
sin cos 0 0 1 0 0 0
θ θ
θ θ
⎡ ⎤ ⎡ ⎤
⎢ ⎥ ⎢ ⎥
[ ]1
90
sin cos 0 0 1 0 0 0
0 0 cos sin 0 0 0 1
TR
θ
θ θ
θ θ=
⎢ ⎥ ⎢ ⎥− −
⎢ ⎥ ⎢ ⎥= =
⎢ ⎥ ⎢ ⎥
⎢ ⎥ ⎢ ⎥
0 0 sin cos 0 0 1 0θ θ⎢ ⎥ ⎢ ⎥
− −⎣ ⎦ ⎣ ⎦
0 1 0 0−⎡ ⎤
⎢ ⎥
1 0 0 0
0 1 0 0
⎡ ⎤
⎢ ⎥
[ ]3
90
1 0 0 0
0 0 0 1
TR
θ =−
⎢ ⎥
⎢ ⎥=
−⎢ ⎥
⎢ ⎥
[ ]2
0
0 1 0 0
0 0 1 0
0 0 0 1
TR
θ =
⎢ ⎥
⎢ ⎥=
⎢ ⎥
⎢ ⎥
⎣ ⎦ 0 0 1 0
⎢ ⎥
⎣ ⎦0 0 0 1
⎢ ⎥
⎣ ⎦
Dept. of CE, GCE Kannur Dr.RajeshKN

79. [ ]
1 1 0 0
1 1 0 0
0 707R
⎡ ⎤
⎢ ⎥−
⎢ ⎥=[ ]
1 0 0 0
0 1 0 0
R
−⎡ ⎤
⎢ ⎥−
⎢ ⎥ [ ]5
45
0.707
0 0 1 1
0 0 1 1
TR
θ =
⎢ ⎥=
⎢ ⎥
⎢ ⎥
−⎣ ⎦
[ ]4
180 0 0 1 0
0 0 0 1
TR
θ =
⎢ ⎥=
−⎢ ⎥
⎢ ⎥
−⎣ ⎦⎣ ⎦
[ ]
1 1 0 0
1 1 0 0
−⎡ ⎤
⎢ ⎥
⎢ ⎥[ ]6
45
1 1 0 0
0.707
0 0 1 1
0 0 1 1
TR
θ =−
⎢ ⎥=
−⎢ ⎥
⎢ ⎥
⎣ ⎦0 0 1 1⎣ ⎦
Dept. of CE, GCE Kannur Dr.RajeshKN
79

80. [ ] [ ] [ ][ ]T
S R S R[ ] [ ] [ ][ ]1 1 1 1MS T M TS R S R=
0 1 0 0 1 0 1 0 0 1 0 0
1 0 0 0 0 0 0 0 1 0 0 01
T
−⎡ ⎤ ⎡ ⎤ ⎡ ⎤
⎢ ⎥ ⎢ ⎥ ⎢ ⎥− −
⎢ ⎥ ⎢ ⎥ ⎢ ⎥=
0 0 0 1 1 0 1 0 0 0 0 12
0 0 1 0 0 0 0 0 0 0 1 0
⎢ ⎥ ⎢ ⎥ ⎢ ⎥=
−⎢ ⎥ ⎢ ⎥ ⎢ ⎥
⎢ ⎥ ⎢ ⎥ ⎢ ⎥
− −⎣ ⎦ ⎣ ⎦ ⎣ ⎦
0 0 0 0⎡ ⎤0 1 0 0 0 1 0 1− −⎡ ⎤ ⎡ ⎤
0 1 0 11
0 0 0 02
⎡ ⎤
⎢ ⎥−
⎢ ⎥=
⎢ ⎥
⎢ ⎥
1 0 0 0 0 0 0 01
0 0 0 1 0 1 0 12
⎡ ⎤ ⎡ ⎤
⎢ ⎥ ⎢ ⎥
⎢ ⎥ ⎢ ⎥=
− −⎢ ⎥ ⎢ ⎥
⎢ ⎥ ⎢ ⎥
0 1 0 1
⎢ ⎥
−⎣ ⎦0 0 1 0 0 0 0 0
⎢ ⎥ ⎢ ⎥
⎣ ⎦ ⎣ ⎦
Dept. of CE, GCE Kannur Dr.RajeshKN

81. 1 0 1 0−⎡ ⎤
[ ]2
1 0 1 0
0 0 0 01
1 0 1 02
MSS
−⎡ ⎤
⎢ ⎥
⎢ ⎥=
−⎢ ⎥1 0 1 02
0 0 0 0
⎢ ⎥
⎢ ⎥
⎣ ⎦
[ ]
0 1 0 0 1 0 1 0 0 1 0 0
1 0 0 0 0 0 0 0 1 0 0 01
T
S
− − −⎡ ⎤ ⎡ ⎤ ⎡ ⎤
⎢ ⎥ ⎢ ⎥ ⎢ ⎥
⎢ ⎥ ⎢ ⎥ ⎢ ⎥[ ]3
0 0 0 1 1 0 1 0 0 0 0 12
0 0 1 0 0 0 0 0 0 0 1 0
MSS ⎢ ⎥ ⎢ ⎥ ⎢ ⎥=
− − −⎢ ⎥ ⎢ ⎥ ⎢ ⎥
⎢ ⎥ ⎢ ⎥ ⎢ ⎥
⎣ ⎦ ⎣ ⎦ ⎣ ⎦
0 1 0 0 0 1 0 1
1 0 0 0 0 0 0 01
−⎡ ⎤ ⎡ ⎤
⎢ ⎥ ⎢ ⎥
0 0 0 0
0 1 0 11
⎡ ⎤
⎢ ⎥1 0 0 0 0 0 0 01
0 0 0 1 0 1 0 12
0 0 1 0 0 0 0 0
⎢ ⎥ ⎢ ⎥−
⎢ ⎥ ⎢ ⎥=
−⎢ ⎥ ⎢ ⎥
⎢ ⎥ ⎢ ⎥
⎣ ⎦ ⎣ ⎦
0 1 0 11
0 0 0 02
0 1 0 1
⎢ ⎥−
⎢ ⎥=
⎢ ⎥
⎢ ⎥
⎣ ⎦
Dept. of CE, GCE Kannur Dr.RajeshKN
81
0 0 1 0 0 0 0 0−⎣ ⎦ ⎣ ⎦ 0 1 0 1−⎣ ⎦

82. 1 0 1 0−⎡ ⎤
⎢ ⎥
[ ]4
0 0 0 01
1 0 1 02
0 0 0 0
MSS
⎢ ⎥
⎢ ⎥=
−⎢ ⎥
⎢ ⎥
⎣ ⎦0 0 0 0⎣ ⎦
1 1 0 0 1 0 1 0 1 1 0 0
T
−⎡ ⎤ ⎡ ⎤ ⎡ ⎤
⎢ ⎥ ⎢ ⎥ ⎢ ⎥
[ ]5
1 1 0 0 0 0 0 0 1 1 0 01
0.707 0.707
0 0 1 1 1 0 1 0 0 0 1 12.83
MSS
⎡ ⎤ ⎡ ⎤ ⎡ ⎤
⎢ ⎥ ⎢ ⎥ ⎢ ⎥− −
⎢ ⎥ ⎢ ⎥ ⎢ ⎥=
−⎢ ⎥ ⎢ ⎥ ⎢ ⎥
⎢ ⎥ ⎢ ⎥ ⎢ ⎥
0 0 1 1 0 0 0 0 0 0 1 1
⎢ ⎥ ⎢ ⎥ ⎢ ⎥
− −⎣ ⎦ ⎣ ⎦ ⎣ ⎦
1 1 0 0 1 1 1 1
1 1 0 0 0 0 0 0
0.1766
0 0 1 1 1 1 1 1
− − −⎡ ⎤ ⎡ ⎤
⎢ ⎥ ⎢ ⎥
⎢ ⎥ ⎢ ⎥=
⎢ ⎥ ⎢ ⎥
1 1 1 1
1 1 1 1
0.1766
1 1 1 1
− −⎡ ⎤
⎢ ⎥− −
⎢ ⎥=
⎢ ⎥0 0 1 1 1 1 1 1
0 0 1 1 0 0 0 0
− − −⎢ ⎥ ⎢ ⎥
⎢ ⎥ ⎢ ⎥
⎣ ⎦ ⎣ ⎦
1 1 1 1
1 1 1 1
− −⎢ ⎥
⎢ ⎥
− −⎣ ⎦
Dept. of CE, GCE Kannur Dr.RajeshKN

83. 1 1 0 0 1 0 1 0 1 1 0 0
T
⎡ ⎤ ⎡ ⎤ ⎡ ⎤
[ ]6
1 1 0 0 1 0 1 0 1 1 0 0
1 1 0 0 0 0 0 0 1 1 0 01
0.707 0.707
0 0 1 1 1 0 1 0 0 0 1 12.83
MSS
− − −⎡ ⎤ ⎡ ⎤ ⎡ ⎤
⎢ ⎥ ⎢ ⎥ ⎢ ⎥
⎢ ⎥ ⎢ ⎥ ⎢ ⎥=
− − −⎢ ⎥ ⎢ ⎥ ⎢ ⎥0 0 1 1 1 0 1 0 0 0 1 12.83
0 0 1 1 0 0 0 0 0 0 1 1
⎢ ⎥ ⎢ ⎥ ⎢ ⎥
⎢ ⎥ ⎢ ⎥ ⎢ ⎥
⎣ ⎦ ⎣ ⎦ ⎣ ⎦
1 1 1 1
1 1 1 1
− −⎡ ⎤
⎢ ⎥
1 1 0 0 1 1 1 1
1 1 0 0 0 0 0 0
− −⎡ ⎤ ⎡ ⎤
⎢ ⎥ ⎢ ⎥ 1 1 1 1
0.177
1 1 1 1
1 1 1 1
⎢ ⎥− −
⎢ ⎥=
− −⎢ ⎥
⎢ ⎥
− −⎣ ⎦
1 1 0 0 0 0 0 0
0.177
0 0 1 1 1 1 1 1
0 0 1 1 0 0 0 0
⎢ ⎥ ⎢ ⎥−
⎢ ⎥ ⎢ ⎥=
− −⎢ ⎥ ⎢ ⎥
⎢ ⎥ ⎢ ⎥
−⎣ ⎦ ⎣ ⎦ 1 1 1 1⎣ ⎦0 0 1 1 0 0 0 0⎣ ⎦ ⎣ ⎦
Dept. of CE, GCE Kannur Dr.RajeshKN

84. Assembled global stiffness matrix
1 1
0 0.1766 0 0 0.1766 0 0 0.1766 0.1766 0
2 2
1 1
+ + + + − − −
⎡ ⎤
⎢ ⎥
⎢ ⎥
⎢ ⎥
g
1 1
0 0 0.1766 0 0.1766 0 0.1766 0.1766 0 0
2 2
1 1
0 0 0 0.1766 0 0 0.1766 0 0.1766 0.1766
2 2
1 1
+ + + + − − −
+ + + − − −
⎢ ⎥
⎢ ⎥
⎢ ⎥
⎢ ⎥
⎢ ⎥
⎢ ⎥
[ ]
1 1
0 0 0 0.1766 0 0.1766 0 0 0.1766 0.1766
2 2
1 1
0.1766 0.1766 0 0 0.1766 0 0 0.
2 2
JS
− + − + + −
=
− − − + + + + 1766 0 0
1 1
0 1766 0 1766 0 0 0 0 0 1766 0 0 1766 0
⎢ ⎥
⎢ ⎥
⎢ ⎥
⎢ ⎥
⎢ ⎥
⎢ ⎥
⎢ ⎥1 1
0.1766 0.1766 0 0 0 0 0.1766 0 0.1766 0
2 2
1 1
0 0.1766 0.1766 0 0 0 0.1766 0 0 0.1766
2 2
1 1
0 0 0 1766 0 1766 0 0 0 0 1766 0 0 1766
⎢ ⎥− − + + + + −
⎢ ⎥
⎢ ⎥
⎢ − − + + + − ⎥
⎢ ⎥
⎢ ⎥
+ + +⎢ ⎥0 0 0.1766 0.1766 0 0 0 0.1766 0 0.1766
2 2
− − + − + +⎢ ⎥
⎣ ⎦
1 2 8
0D D D= = =Boundary conditions are:
Dept. of CE, GCE Kannur Dr.RajeshKN
1 2 8
0D D DBoundary conditions are:

85. 0.677 -0.177 -0.500 0.000 -0.177⎡ ⎤
⎢ ⎥
Reduced stiffness matrix
[ ]
-0.177 0.677 0.000 0.000 0.177
-0.500 0.000 0.677 0.177 0.000FFS =
⎢ ⎥
⎢ ⎥
⎢ ⎥
⎢ ⎥
[ ]
0.000 0.000 0.177 0.677 0.000
-0.177 0.177 0.000 0.000 0.677
⎢ ⎥
⎢ ⎥
⎢ ⎥⎣ ⎦⎣ ⎦
Dept. of CE, GCE Kannur Dr.RajeshKN
85

86. 5⎧ ⎫
⎪ ⎪
{ }
0
0FCA
⎪ ⎪
⎪ ⎪⎪ ⎪
= ⎨ ⎬
⎪ ⎪
In this problem, the reduced load vector
(in global coords) can be directly written as
0
0
⎪ ⎪
⎪ ⎪
⎪ ⎪⎩ ⎭
{ } [ ] { }
1
F FF FCD S A
−
=
24.144⎧ ⎫
⎪ ⎪
4.829 1.000 3.829 -1.000 1.000 5⎡ ⎤ ⎧ ⎫
⎢ ⎥ ⎪ ⎪ 5.000
19.144
⎪ ⎪
⎪ ⎪⎪ ⎪
⎨ ⎬
⎪
=
⎪
1.000 1.793 0.793 -0.207 -0.207
3.829 0.793 4.622 -1.207 0.793=
0
0
⎢ ⎥ ⎪ ⎪
⎢ ⎥ ⎪ ⎪⎪ ⎪
⎢ ⎥ ⎨ ⎬
⎢ ⎥ ⎪ ⎪ -5.000
5.000
⎪
⎪
⎪
⎪
⎪
⎪⎩ ⎭
-1.000 -0.207 -1.207 1.793 -0.207 0
1.000 -0.207 0.793 -0.207 1.793 0
⎢ ⎥ ⎪ ⎪
⎢ ⎥ ⎪ ⎪
⎢ ⎥ ⎪ ⎪⎣ ⎦ ⎩ ⎭
Dept. of CE, GCE Kannur Dr.RajeshKN
⎣ ⎦ ⎩ ⎭

87. Assignment
Dept. of CE, GCE Kannur Dr.RajeshKN