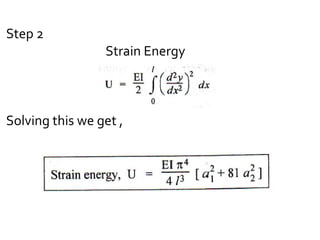
The document discusses numerical methods for solving structural mechanics problems, specifically the Rayleigh Ritz method. It provides an overview of the Rayleigh Ritz method, indicating that it is an integral approach that is useful for solving structural mechanics problems. The document then provides a step-by-step example of using the Rayleigh Ritz method to determine the bending moment and deflection at the mid-span of a simply supported beam subjected to a uniformly distributed load over the entire span.

1. prepared by
R.Sakthivel Murugan,
Assistant Professor, KCET

2. • Engineering Analysis
• Analytical Methods (or) Theoretical Analysis
• Numerical Methods (or) Approximate Methods

3.  Functional Approximation
 Finite Difference Method (FDM)
 Finite Element Method (FEM)

4. -Rayleigh Ritz Method
-Weighted Residual Method

5.  Potential Energy is the capacity to do work.
 Total Potential Energy = Internal Potential
Energy
+External
Potential Energy.
 Principle of minimum potential energy

6.  It is an integral approach method
 Useful for solving Structural Mechanics
Problems.
 It is also known as Variational Approach.

7.  Potential Energy ,
 Total Potential Energy
π = Strain Energy – Work done by external forces
= U- H
∫=Π
2
1
)''','','(
x
x
dxyyyf

8.  It should satisfy the geometric boundary
condition.
 It should have at least one Rayleigh Ritz
parameter.
 It should represented as either polynomial or
trigonometrical.

9. Polynomial  Bar Element
Trignometric  Beam Element
.......3
3
2
210 ++++= xaxaxaay
.....
3
sinsin1 +
Π
+
Π
=
l
x
l
x
ay

11. • Step 1
– Setting an approximation Function
• Step 2
– Determine Strain Energy, U
• Step 3
– Determine Work Done by External Force , H
• Step 4
– Total Potential Energy, π= U-H
• Step 5
– To find Ritz Parameter by Partial Differentiation (step 4 result)
• Step 6
– Determine deflection for beam element
– Determine displacement for bar element
• Step 7
– Determine Bending Moment for beam element
– Determine Stress for bar element

12. A simply supported beam subjected to
uniformly distributed load over entire span.
Determine the bending moment and
deflection at mid span by using Rayleigh Ritz
method.

13. Step 1
Setting approximation function for beam

14. Step 2
Strain Energy
Solving this we get ,

15. Step 3
Work done by External Forces
Solving this we get,
dxyH
l
∫=
0
ω

16. Step 4
Total Potential Energy , π= U- H

17. Step 5
To find Ritz Parameter by Partial
Differentiation
Solving this we get ,
&
So,

18. Step 6
Maximum Deflection
Sub x = l/2 in y 

19. Step 7
Maximum Bending Moment
Solving this we get,
Mmax= -0.124ω2
2
2
dx
yd
EIM =

20. Thank you