Download as PDF, PPTX
Uploaded byMohammad Tawfik
FEM: Bars and Trusses
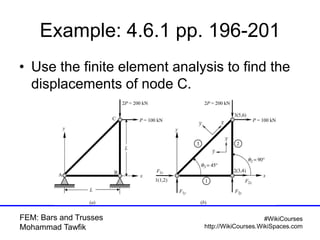
This document provides an introduction to the finite element method (FEM) applied to bars and trusses, detailing calculations for displacement fields using steel and aluminum elements. It outlines the stiffness matrices for different material properties and discusses the assembly of these matrices while applying boundary conditions. The lecture concludes with a summary of the application of FEM to bar problems with various orientations.
More Related Content
Similar to FEM: Bars and Trusses
FEM: Bars and Trusses
- 1. FEM: Bars andTrusses Mohammad Tawfik #WikiCourses http://WikiCourses.WikiSpaces.com Introduction to the Finite Element Method Bars and Trusses
- 2. FEM: Bars andTrusses Mohammad Tawfik #WikiCourses http://WikiCourses.WikiSpaces.com Bar Example (Ex. 4.5.2, p. 187) • Consider the bar shown in the above figure. • It is composed of two different parts. One steel tapered part, and uniform Aluminum part. • Calculate the displacement field using finite element method.
- 3. FEM: Bars andTrusses Mohammad Tawfik #WikiCourses http://WikiCourses.WikiSpaces.com Bar Example • The bar may be represented by two elements. • The stiffness matrices of the two elements may be obtained using the following integration: 2 1 2 1 22 22 21 2 1 11 11 x x ee ee x x e dx hh hh xEAdx dx d dx d dx d dx d xEAK
- 4. FEM: Bars andTrusses Mohammad Tawfik #WikiCourses http://WikiCourses.WikiSpaces.com Bar Example • For the Aluminum bar: E=107 psi, and A=1 in2. we get: • For the Steel bar: E=38107 psi, and A=(1.5-0.5x/96) in2. we get: 11 11 120 10 11 11 120 10 7 2 7 2 1 x x Al dxK 11 11 96 10.75.4 11 11 96 5.0 5.1 96 10.3 7 2 7 2 1 x x Fe dx x K
- 5. FEM: Bars andTrusses Mohammad Tawfik #WikiCourses http://WikiCourses.WikiSpaces.com Bar Example • Assembling the Stiffness matrix and utilizing the external forces, we get: • The boundary conditions may be applied and the system of equations solved. 0 0 10 10.2 0 33.833.80 33.88.575.49 05.495.49 10 5 5 3 2 1 4 R u u u
- 6. FEM: Bars andTrusses Mohammad Tawfik #WikiCourses http://WikiCourses.WikiSpaces.com Bar Example • Solving, we get: • For the secondary variables: in u u 181.0 061.0 3 2 lbR 30000
- 7. FEM: Bars andTrusses Mohammad Tawfik #WikiCourses http://WikiCourses.WikiSpaces.com Trusses • A truss is a set of bars that are connected at frictionless joints. • The Truss bars are generally oriented in the plain.
- 8. FEM: Bars andTrusses Mohammad Tawfik #WikiCourses http://WikiCourses.WikiSpaces.com Trusses • Now, the problem lies in the transformation of the local displacements of the bar, which are always in the direction of the bar, to the global degrees of freedom that are generally oriented in the plain.
- 9. FEM: Bars andTrusses Mohammad Tawfik #WikiCourses http://WikiCourses.WikiSpaces.com Equation of Motion 0 0 0000 0101 0000 0101 2 1 2 2 1 1 F F v u v u h EA
- 10. FEM: Bars andTrusses Mohammad Tawfik #WikiCourses http://WikiCourses.WikiSpaces.com Transformation Matrix DOF dTransforme DOFLocal v u v u CosSin SinCos CosSin SinCos v u v u 2 2 1 1 2 2 1 1 00 00 00 00 DOF dTransforme DOFLocal T
- 11. FEM: Bars andTrusses Mohammad Tawfik #WikiCourses http://WikiCourses.WikiSpaces.com The Equation of Motion Becomes • Substituting into the FEM: • Transforming the forces: • Finally: FTK FTTKT TT FK
- 12. FEM: Bars andTrusses Mohammad Tawfik #WikiCourses http://WikiCourses.WikiSpaces.com Recall TKTK T CosSin SinCos CosSin SinCos T 00 00 00 00 Where: 0000 0101 0000 0101 h EA K
- 13. FEM: Bars andTrusses Mohammad Tawfik #WikiCourses http://WikiCourses.WikiSpaces.com Element Stiffness Matrix in Global Coordinates CosSin SinCos CosSin SinCos CosSin SinCos CosSin SinCos h EA K 00 00 00 00 0000 0101 0000 0101 00 00 00 00
- 14. FEM: Bars andTrusses Mohammad Tawfik #WikiCourses http://WikiCourses.WikiSpaces.com Element Stiffness Matrix in Global Coordinates 22 22 22 22 2 2 1 2 2 1 2 2 1 2 2 1 2 2 1 2 2 1 2 2 1 2 2 1 SinSinSinSin SinCosSinCos SinSinSinSin SinCosSinCos h EA K
- 15. FEM: Bars andTrusses Mohammad Tawfik #WikiCourses http://WikiCourses.WikiSpaces.com Example: 4.6.1 pp. 196-201 • Use the finite element analysis to find the displacements of node C.
- 16. FEM: Bars andTrusses Mohammad Tawfik #WikiCourses http://WikiCourses.WikiSpaces.com Element Equations 0000 0101 0000 0101 1 L EA K 1010 0000 1010 0000 2 L EA K 3536.03536.03536.03536.0 3536.03536.03536.03536.0 3536.03536.03536.03536.0 3536.03536.03536.03536.0 3 L EA K
- 17. FEM: Bars andTrusses Mohammad Tawfik #WikiCourses http://WikiCourses.WikiSpaces.com Assembly Procedure 3536.13536.0103536.03536.0 3536.03536.0003536.03536.0 101000 000101 3536.03536.0003536.03536.0 3536.03536.0013536.03536.1 L EA K
- 18. FEM: Bars andTrusses Mohammad Tawfik #WikiCourses http://WikiCourses.WikiSpaces.com Global Force Vector P P F F F F F F F F F F F y x y x y x y x y x 2 2 2 1 1 3 3 2 2 1 1 Remember! NO distributed load is applied to a truss
- 19. FEM: Bars andTrusses Mohammad Tawfik #WikiCourses http://WikiCourses.WikiSpaces.com Boundary Conditions 02211 VUVU Remove the corresponding rows and columns P P V U L EA 23536.13536.0 3536.03536.0 3 3 Continue! (as before)
- 20. FEM: Bars andTrusses Mohammad Tawfik #WikiCourses http://WikiCourses.WikiSpaces.com Results EA PL V EA PL U 3 ,828.5 33 PFF PFPF yx yx 3,0 ,, 22 11
- 21. FEM: Bars andTrusses Mohammad Tawfik #WikiCourses http://WikiCourses.WikiSpaces.com Postcomputation e e e e e A P A P 21 e e ee e e u u L EA P P 2 1 2 1 11 11 2 2 1 1 2 2 1 1 00 00 00 00 v u v u CosSin SinCos CosSin SinCos v u v u
- 22. FEM: Bars andTrusses Mohammad Tawfik #WikiCourses http://WikiCourses.WikiSpaces.com Postcomputation A P A P 2, 3 ,0 )3()2()1(
- 23. FEM: Bars andTrusses Mohammad Tawfik #WikiCourses http://WikiCourses.WikiSpaces.com Summary • In this lecture we learned how to apply the finite element modeling technique to bar problems with general orientation in a plain.