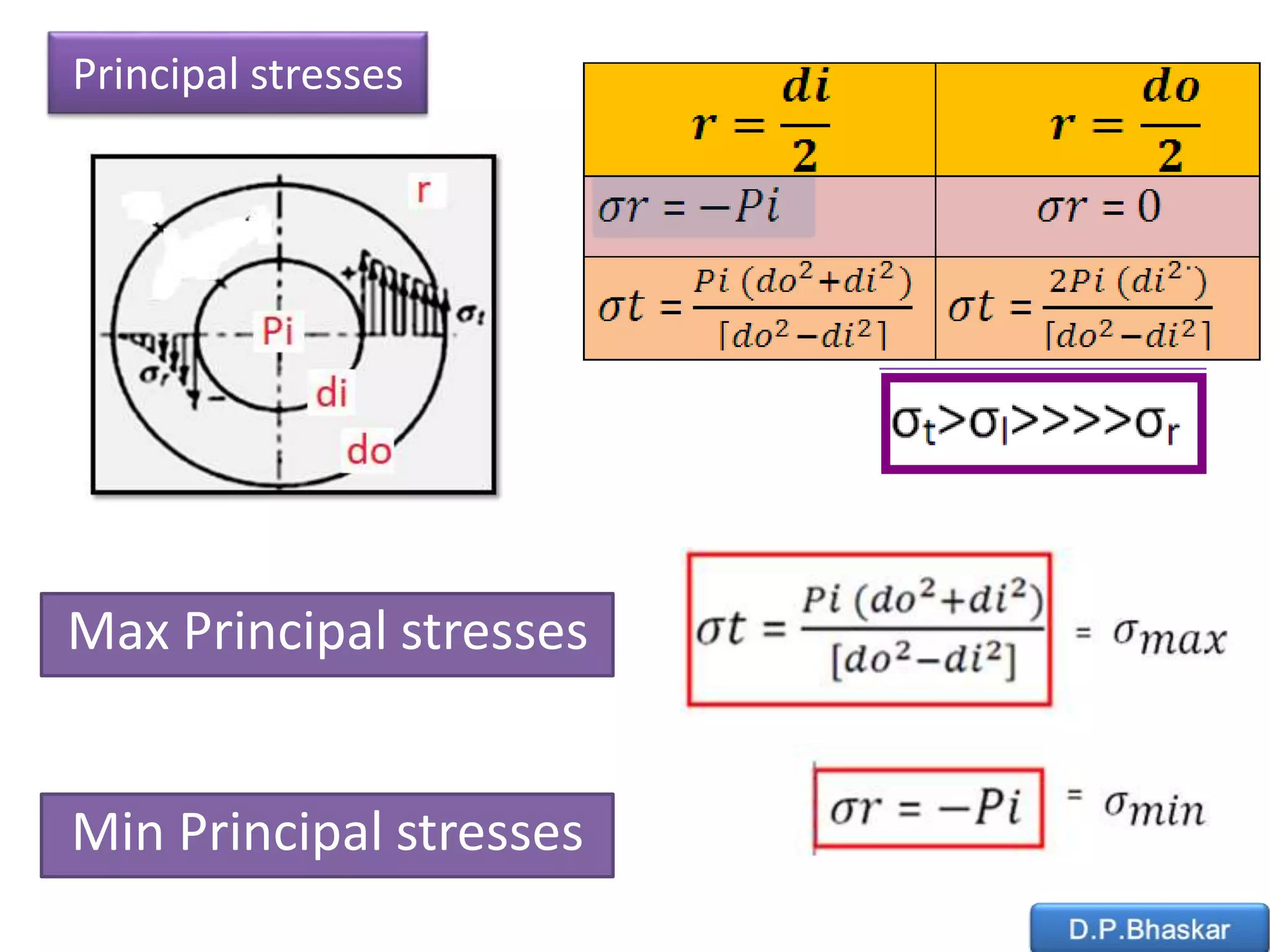
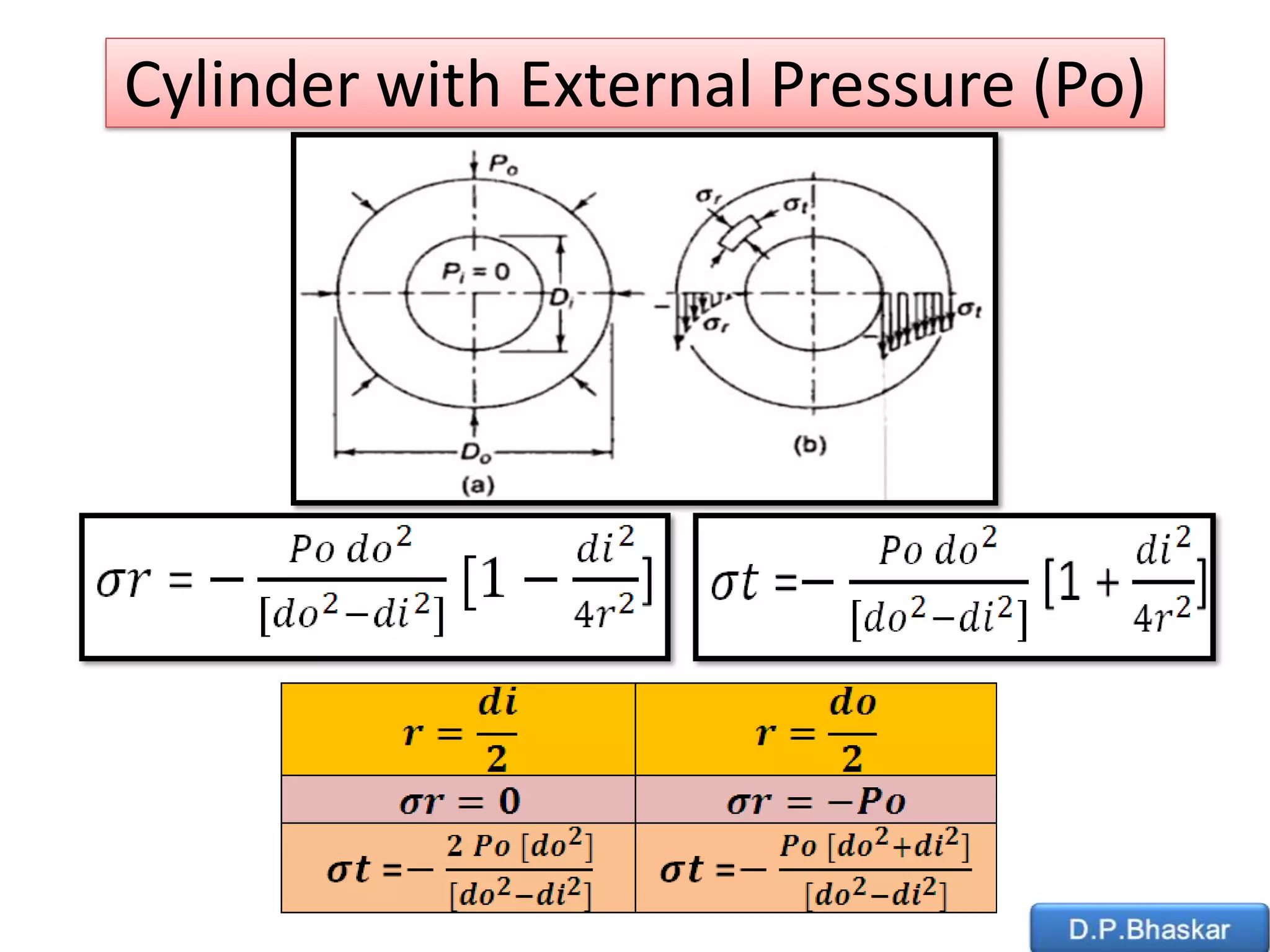
1) The document discusses stresses in thin and thick cylinders, including circumferential (hoop), longitudinal, and radial stresses. It also covers principal stresses. 2) Formulas are provided for calculating wall thickness based on tangential stress in thin cylinders, and Lame's equation is introduced for thick cylinders. 3) Additional concepts covered include stresses in spherical vessels, pre-stressing techniques like autofrettage to increase pressure capacity, and stresses in cylinders under external pressure or combined internal and shrink pressures.

1. Cylinder
• Thin cylinder/
Spherical vessel Thick Cylinder
Cylinder and Pressure Vessel

2. 1]Circumferential /Hoop stress/Tangential:
Exerted circumferentially on every particle in the cylinder wall.
• Can be imagined as a band surrounding a barrel.
• When barrel expands, the band stretches and undergoes stress.
3]Radial stress: (Compressive)
Caused by the design pressures acting through the wall thickness
(neglected). As P small
2]Longitudinal stress:
Parallel to the axis of cylindrical
Stretching the shell
circumferentially
Stresses in Thin Cylinder

3. Tangential/Circumferential/Hoop stress
Stress in Thin Cylinder
Assumption:
Hoop stress is uniformly distributed through t
(Because t is small in) Cylinder

4. Longitudinal/Axial Stress

5. Radial Stress in Thin Cylinder (σr)
Pi : Very Less : σr is neglected
t : Less
Assumption:
Radial stress is neglected as P is very small

6. Principal Stresses in Thin Cylinder
SO: thickness is calculated using tangential stress
σt
σL
σr

7. Stress in Spherical vessel
Spherical pressure vessel has
twice the strength of a
Cylindrical pressure vessel

8. Seamless cylinder.
Storage capacity=0.25 m3,. Pi=20Mpa. L= 2di,
20C8 ( Sut=390 Mpa), FoS=2.5. Dimensions?
Q

9. Air receiver:
Storage capacity: 0.25 m3
Operating pressure: Pi=5 Mpa
10C8 (Sult=340Mpa)
FoS=4
Neglect weld efficiency.
Dimensions of receiver:?
Q

11. Stresses in Thick Cylinder CBS

12. Cylinder with Internal Pressure (Pi)

13. Max Principal stresses
Min Principal stresses
Principal stresses

14. Lame’s Equation
Wall thickness of shell t=
Theories of failure

15. Clavarino’s & Birnie’s equation /St Venants theory
Clavarino’s Eq
Closed cylinder

16. Birnie’s
Open cylinder
Clavarino’s & Birnie’s equation /St Venants theory

17. Cylinder with External Pressure (Po)

18. : Pre-Stressing
When subjected to Pi ,
Hoop stress σt limits pressure capacity
Autofrettage is method to increase the
pressure capacity of cylinder
Used for HP Cylinder, Gun Barrels

19. • Cylinder subjected to immense pressure, which causes
the internal parts of the vessel to yield, thus resulting in
internal compressive residual stresses.
•It increases pressure capacity of cylinder
•Residuals compressive stresses close the cracks
•For same thickness cylinder can be used for Pi more than designed.

20. Wire under tension is closely wound the cylinder results in
residual compressive stresses

21. P= Pi (Outer cylinder)
P= Po (Inner cylinder)

23. Deformations in Jacket and cylinder

26. Shrink Pressure P=38.46Mpa
Internal Pressure Pi=300Mpa
D1=20mm
D2=40mm
D3=60mm
Resultant stresses??

27. Stress due to Shrink Pressure [P=38.46] Jacket
Stress due to Shrink Pressure [P=38.46] Cylinder

29. Stress due to Internal Pressure [Pi=300]

30. Resultant

32. σtmax in each cylinder
is same. Shrink Pressure P=?
Internal Pressure Pi=35
D1=50
D2=75
D3=100
E=207 KN/mm2
Jacket D2* =? D2* =75-δ

33. Stress due to Internal Pressure [Pi]

34. Stress due to Shrink Pressure [P]
Cylinder
Jacket

35. Maximum tangential
stress in both tube has
same magnitude

37. END

38. Cylinder with Internal Pressure (Pi)
CBS

39. CBS

40. CBS