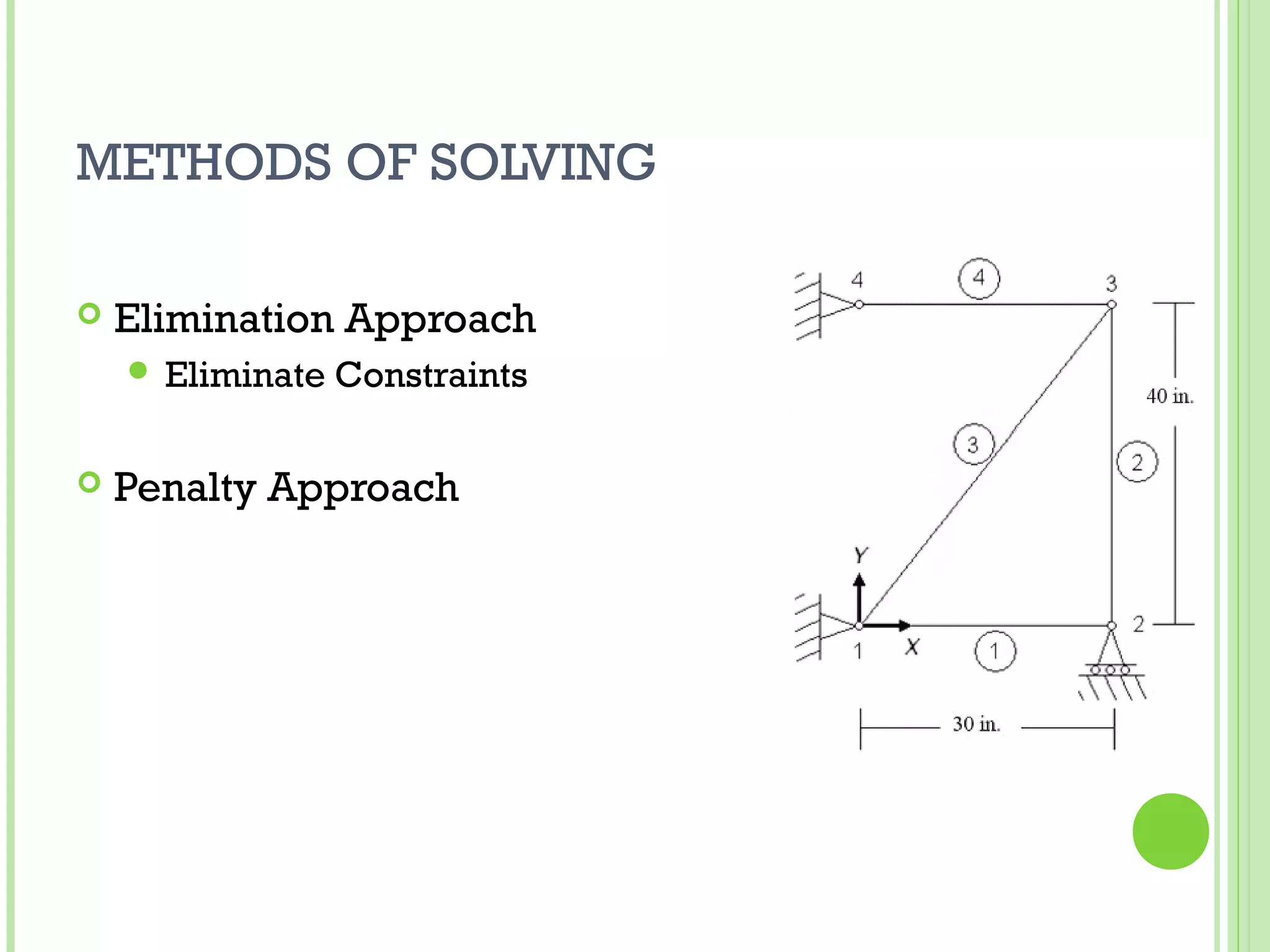
The document provides an overview of the finite element method (FEM), detailing its historical development and applications in solving partial differential equations through numerical methods. It discusses the evolution of FEM from early predictions of natural frequency to the integration of FEM with computer-aided design (CAD) in product design processes. Key concepts, one-dimensional rod elements, and two-dimensional trusses are also explained, highlighting methods of analysis such as Rayleigh-Ritz and Galerkin's method.

1. FINITE ELEMENT METHOD

2. INTRODUCTION
 What is finite element analysis, FEM?
 A Brief history of FEM
 What is FEM used for?
 1D Rod Elements, 2D Trusses

3. FINITE ELEMENT METHOD –
WHAT IS IT?
 The Finite Element Method (FEM) is a
numerical method of solving systems of partial
differential equations (PDEs)
 It reduces a PDE system to a system of
algebraic equations that can be solved using
traditional linear algebra techniques.
 In simple terms, FEM is a method for dividing
up a very complicated problem into small
elements that can be solved in relation to each
other.

4. Overview of the Finite
Element Method
( S ) ⇔(W ) ≈ ( G ) ⇔( M )
Strong Weak Galerkin Matrix
form form approx. form

5. 1. Lord John William Strutt Rayleigh (late 1800s), developed a
method for predicting the first natural frequency of simple
structures. It assumed a deformed shape for a structure and
then quantified this shape by minimizing the distributed energy
in the structure.
2. Ritz then exp Walter ended this into a method, now known as
the Rayleigh-Ritz method, for predicting the stress and
displacement behavior of structures.

6. 3. Dr. Ray Clough coined the term “finite element” in 1960. The 1960s saw
the true beginning of commercial FEA as digital computers replaced analog
ones with the capability of thousands of operations per second.
4. In the 1950s, a team form Boeing demonstrated that complex surfaces
could be analyzed with a matrix of triangular shapes.
5. In 1943, Richard Courant proposed breaking a continuous system into
triangular segments. (The unveiling of ENIAC at the University of
Pennsylvania.)
6. In the early 1960s, the MacNeal-Schwendle Corporation (MSC) develop a
general purpose FEA code. This original code had a limit of 68,000
degrees of freedom. When the NASA contract was complete, MSC
continued development of its own version called MSC/NASTRAN, while the
original NASTRAN become available to the public and formed the basis of
dozens of the FEA packages available today. Around the time 6
MSC/NASTRAN was released, ANSYS, MARC, and SAP were introduced.

7. 7. By the 1970s, Computer-aided design, or CAD, was introduced later in the
decade.
8. standards such as IGES and DXF. Permitted limited geometry transfer
between the systems.
9. In the 1980s,CAD progressed from a 2D drafting tool to a 3D surfacing tool,
and then to a 3D sIn the 1980s, the use of FEA and CAD on the same
workstation with developing geometry olid modeling system. Design
engineers began to seriously consider incorporating FEA into the general
product design process.
10. As the 1990s draw to a place, the PC platform has become a major force in
high end analysis. The technology has become to accessible that it is
actually being “hidden” inside CAD packages.
7

8. BASIC CONCEPTS
 Loads
 
f T Pi
 Equilibrium ~
σ ji , j + fi = 0
 Boundary conditions

9. DEVELOPMENT OF THEORY
 Rayleigh-Ritz Method
 Total potential energy equation
 Galerkin’s Method

10. 1D ROD ELEMENTS
 To understand and solve 2D and 3D problems we must
understand basic of 1D problems.
 Analysis of 1D rod elements can be done using
Rayleigh-Ritz and Galerkin’s method.
 To solve FEA problems same are modified in the
Potential-Energy approach and Galerkin’s approach

11. 1D ROD ELEMENTS
 Loading consists of three types : body force f , traction
force T, point load Pi
 Body force: distributed force , acting on every
elemental volume of body i.e. self weight of body.
 Traction force: distributed force , acting on surface of
body i.e. frictional resistance, viscous drag and surface
shear
 Point load: a force acting on any single point of element

12. 1D ROD ELEMENTS Element -1 Element-2
1 T e 
 Element strain energy U e = q [k ]q
2
 Element stiffness matrix
E e Ae  1 − 1
[k ] =
e
− 1 1 
le  
 Load vectors
 Element body load vector
 Element traction-force vector  e Ae l e f 1
f = 
2 1
 e Tl e 1
T = 
2 1

13. 2D TRUSS
 2 DOF
 Transformations
 Modified Stiffness Matrix
 Methods of Solving

14. 2D TRUSS
 Transformation Matrix
 Direction Cosines
le = ( x2 − x1 ) 2 + ( y 2 − y1 ) 2
x 2 − x1
l m 0 0  l = cos θ =
[ L] =  le
 0 0 l m

y 2 − y1
m = sin θ =
le

15. 2D TRUSS
 Element Stiffness Matrix
 l2 lm − l 2 − lm 
 2
E e Ae  lm m2 − lm − m 
[k e ] =
l e  − l 2 − lm l2 lm 
 2 
− lm − m
2
 lm m  

16. METHODS OF SOLVING
 Elimination Approach
 Eliminate Constraints
 Penalty Approach

17. ELIMINATION METHOD
 Set defection at the constraint to equal zero

18. ELIMINATION METHOD
 Modified Equation
 DOF’s 1,2,4,7,8 equal to zero

19. 2D TRUSS
 Element Stresses
Ee 
σ= [ − l − m l m] q
le
 Element Reaction Forces
 
R = [ K ]Q

20. 2D TRUSS
 Development of Tables
 Coordinate Table
 Connectivity Table
 Direction Cosines Table

21. 2D TRUSS
 Coordinate Table
 E.g;

22. 2D TRUSS
 Connectivity Table
 E.g;

23. 2D TRUSS
le = ( x2 − x1 ) 2 + ( y 2 − y1 ) 2
x 2 − x1
l = cos θ =
le
y 2 − y1
m = sin θ =
le

24. 3D TRUSS STIFFNESS MATRIX
 3D Transformation Matrix
 Direction Cosines
 l m n 0 0 0
[ L] = 
 0 0 0 l m n

le = ( x 2 − x1 ) 2 + ( y 2 − y1 ) 2 + ( z 2 − z1 ) 2
x 2 − x1 y 2 − y1 z 2 − z1
l = cos θ = m = cos φ = n = cos ϕ =
le le le

25. 3D TRUSS STIFFNESS MATRIX
 3D Stiffness Matrix
 l2 lm ln − l 2 − lm − ln 
 
 lm m2 mn − lm − m 2 − mn 
E e Ae  ln mn n2 − ln − mn − n 2 
[k e ] =  
l e  − l 2 − lm − ln l 2
lm ln 
− lm − m 2 − mn lm m2 mn 
 
 − ln − mn − n
2 2
 ln mn n  

26. EXAMPLE 1D ROD ELEMENTS
Example 1
Problem statement: (Problem 3.1 from Chandrupatla and Belegunda’s
book)
Consider the bar in Fig.1, determine the following by hand calculation:
1) Displacement at point P 2) Strain and stress
3) Element stiffness matrix 4) strain energy in element
Given:
E = 30 ×106 psi q1 = 0.02in
Ae = 1.2 in 2 q2 = 0.025in

27. Solution:
1) Displacement (q) at point P
We have
Now linear shape functions N1( ) and N2( ) are given by
And

30. EXAMPLE 2D TRUSS

36. CONCLUSION
 Good at Hand Calculations, Powerful when
applied to computers
 Only limitations are the computer limitations

37. MATLAB PROGRAM TRUSS2D.M

38. REFERENCES