Skip to main content
UploadLanguage (EN)Support
BusinessMobileSocial MediaMarketingTechnologyArt & PhotosCareerDesignEducationPresentations & Public SpeakingGovernment & NonprofitHealthcareInternetLawLeadership & ManagementAutomotiveEngineeringSoftwareRecruiting & HRRetailSalesServicesScienceSmall Business & EntrepreneurshipFoodEnvironmentEconomy & FinanceData & AnalyticsInvestor RelationsSportsSpiritualNews & PoliticsTravelSelf ImprovementReal EstateEntertainment & HumorHealth & MedicineDevices & HardwareLifestyle
Mahdi Damghani, profile picture
Uploaded byMahdi Damghani
PPTX, PDF7,280 views

Fatigue Analysis of Structures (Aerospace Application)

This document provides an introduction to fatigue analysis of aerospace structures. It discusses key topics including stress-life analysis methods, S-N curves, stress concentration factors, notch sensitivity, and fatigue failure locations. Examples of fatigue critical locations in aircraft components like flaps, struts, and baffle panels are also shown. The document concludes with examples calculating stresses, stress ratios, and fatigue life based on the stress-life approach.

Engineering◦
Downloaded 520 times
Aero Structure-Fatigue Analysis By Dr. Mahdi Damghani 2016-2017 1
Suggested Readings Reference 1 Reference 2 2 Chapter 10 of Ref [1], Chapter 6 of Ref [2], Chapter 4 of Ref [3] Reference 3
Topics • Familiarisation with fatigue of metals • Life estimates • Endurance limit • Fluctuating stresses • Stress concentration and Notch sensitivity 3
Your Questions • Feel free to ask your questions in the following link: https://padlet.com/mahdi_damghani/Fatigue_Analysis 4
Introduction • In most testing of those properties of materials that relate to the stress-strain diagram, the load is applied gradually, to give sufficient time for the strain to fully develop. • Furthermore, the specimen is tested to destruction, and so the stresses are applied only once • Testing of this kind is applicable, to what are known as static conditions • The condition frequently arises, however, in which the stresses vary with time or they fluctuate between different levels. • For example, a particular fiber on the surface of a rotating shaft subjected to the action of bending loads undergoes both tension and compression for each revolution of the shaft. 5
Introduction 6 Taken from: http://science.howstuffworks.com/transport/flig ht/modern/air-traffic-control1.htm Push back from the gate, taxi to the runway Speeding down the runway Climbing to cruising altitude Descending and Manoeuvring to the destination Aligning the plane with runway Landing, taxis to the gate and parking at terminal
Introduction • Some cyclic loads in aircrafts; • Push back (on landing gear) • Turning (high stresses on landing gear) • Taxy • Take off • Cabin pressurisation • Landing impact • Undercarriage loading • Global/local turbulence • Gust and manoeuvre 7
Introduction • Often, machine members are found to have failed under the action of repeated or fluctuating stresses • The most careful analysis reveals that the actual maximum stresses were well below the ultimate strength of the material, and quite frequently even below the yield strength • The most distinguishing characteristic of these failures is that the stresses have been repeated a very large number of times. Hence the failure is called a fatigue failure 8
Introduction • Fatigue failure • Gives no warning (no large deflection etc) and it is very sudden=brittle fracture • Dangerous (because it is sudden) • Complicated phenomenon (partially understood) • Life of a component must be obtained based on empirical methods 9
Introduction 10 Growth of surface micro- cracks of aircraft towbar as the result of fatigue loading leading to failure
Introduction 11
Introduction 12 Fatigue crack at stress raiser (discontinuity, i.e. hole) due to stress concentration
Introduction • Micro-cracks formation on the surface of part due to cyclic plastic deformations • During cyclic loading, these cracked surfaces open and close, rubbing together • The beach mark appearance depends on the changes in the level or frequency of loading and the corrosive nature of the environment • Cracks keep growing up to a critical length and suddenly part fails 13
Fatigue analysis approaches • Stress-life method • Will be covered in the lecture • Strain-life method • Beyond the scope of this lecture • Linear elastic fracture mechanics method • Beyond the scope of this lecture 14 • Generally speaking we have; • Low cycle fatigue (1<=N<=103) • High cycle fatigue (N>103)
Stress-life method • The least accurate method • Specially for low cycle fatigue • Good approximation for high cycle fatigue • Assumes little plastic deformation due to cyclic loading • The most widely used since mid-1800s • A lot of data and understanding is available • Good predictions for high cycle fatigue • Easy to perform 15
Strain-life method • Detailed analysis of the plastic deformation at localized regions where the stresses and strains are considered for life estimates • Good for low-cycle fatigue • Several idealizations must be compounded, and so some uncertainties will exist in the results 16
Fracture mechanics method • The fracture mechanics method assumes a crack is already present and detected • It is then employed to predict crack growth with respect to stress intensity • It is most practical when applied to large structures in conjunction with computer codes and a periodic inspection program • Currently Airbus uses this method in combination with stress-life method 17
Stress-life method • To determine the strength of materials under the action of fatigue loads, specimens are subjected to repeated or varying forces of specified magnitudes while the cycles or stress reversals are counted to destruction • Therefore graphs of subsequent slides (S-N diagrams) can be produced 18
Watch 19
Fatigue machine (for R=-1 only) • R. R. Moore high-speed rotating-beam machine • Specimen is subjected to pure bending (no transverse shear) by means of weights 20 • The specimen is very carefully machined and polished, with a final polishing in an axial direction to avoid circumferential scratches and minimize surface roughness
R. R. Moore machine 21 • When rotated one half revolution, the stresses in the fibers originally below the neutral axis are reversed from tension to compression and vice versa • Upon completing the revolution, the stresses are again reversed so that during one revolution the test specimen passes through a complete cycle of flexural stress (tension and compression).
Electro-hydraulic axial fatigue machine (for all R values) 22
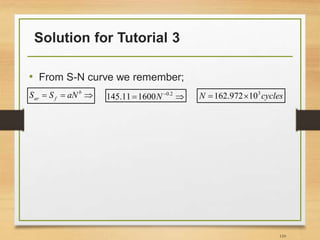
Output from fatigue test (see Ref [3]) 23 The number of cycles to failure is called fatigue life Nf Each cycle is equal to two reversals Stress in the component some books use symbol σ instead time Stress
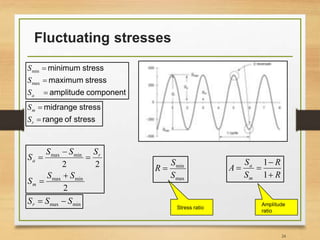
Fluctuating stresses 24 Stress ratio Amplitude ratio 2 22 minmax minmax SS S SSS S m r a      minmax SSSr  R R S S A m a    1 1 max min S S R  componentamplitude stressmaximum stressminimum    aS S S max min stressofrange stressmidrange   r m S S
S-N/Wohler diagram (see Ref [2]) 25 Results of completely reversed axial fatigue tests. Material: UNS G41300 steel, normalized; Sut = 116 kpsi; maximum Sut = 125 kpsi. Often plotted in log-log or semi-log graphs. If plotted in log-log, y axis is in terms of stress amplitude or stress range and x axis in terms of number of reversals or cycles to failure
How SN curve is established 26 w1 w1 w1 3 1 minmax ,25.0 max 24 r anw I My ryrI      
S-N bands for Aluminium alloys for completely reversed cycling 27
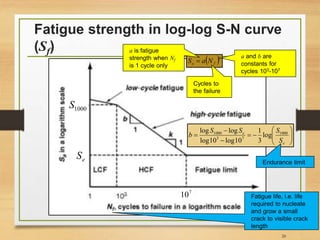
Fatigue strength in log-log S-N curve (Sf) 28           e e S SSS b 1000 73 1000 log 3 1 10log10log loglog Endurance limit Fatigue life, i.e. life required to nucleate and grow a small crack to visible crack length  b fa NaS  eS a and b are constants for cycles 103-107 1000S Cycles to the failure a is fatigue strength when Nf is 1 cycle only 7 10
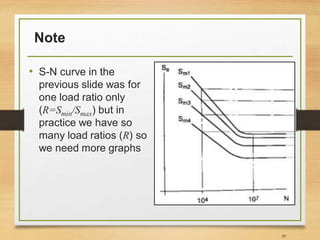
Note • S-N curve in the previous slide was for one load ratio only (R=Smin/Smax) but in practice we have so many load ratios (R) so we need more graphs 29
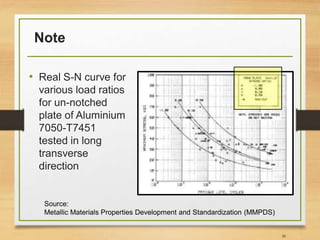
Note 30 • Real S-N curve for various load ratios for un-notched plate of Aluminium 7050-T7451 tested in long transverse direction Source: Metallic Materials Properties Development and Standardization (MMPDS)
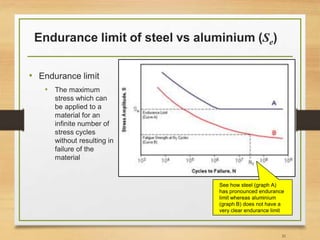
Endurance limit of steel vs aluminium (Se) • Endurance limit • The maximum stress which can be applied to a material for an infinite number of stress cycles without resulting in failure of the material 31 See how steel (graph A) has pronounced endurance limit whereas aluminium (graph B) does not have a very clear endurance limit
Endurance limit (Se) • For example for steel material the endurance limit can be obtained by the following relationship; • Note that this is achieved from experiments and is for fatigue test specimen not real life loading 32
Endurance limit (Se) • In real life endurance limit can be different due to many factors (see Ref [2] for more details); 33
Fatigue prone locations • The following locations in the structure are prone to fatigue failure (formation of crack) due to stress concentration and therefore illustrated in subsequent slides; • Holes • Notches • Lugs • Pins • Fillets • Joints 34
Stress Concentration and Notch Sensitivity • Any discontinuity in a machine part alters the stress distribution in the immediate vicinity of the discontinuity • Elementary stress equations no longer describe the state of stress in the part at these locations • Such discontinuities are called stress raisers, • Regions in which they occur are called areas of stress concentration 35
Stress concentration 36 NotchHoleHole
Stress concentration in aircraft 37
Stress Concentration around a circular hole subjected to remote loading in an infinite composite panel 38
Stress concentration factor • A theoretical, or geometric, stress-concentration factor Kt or Kts is used to relate the actual maximum stress at the discontinuity to the nominal stress (remote stress) • Stress concentration factor depends on; • The geometry of structure • Type of loading (uni-axial, bi-axial, bending moment etc) 39
How to get stress concentration value? • Experimental procedures • Photoelasticity • grid methods • brittle-coating methods • Electrical strain-gauge methods 40 • Finite element analysis • Not exact • Analytical approaches based on conformal mapping and complex algebra
Stress concentration value 41
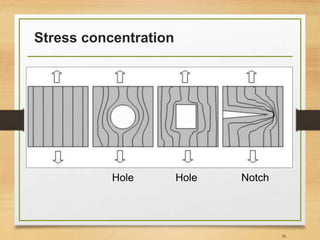
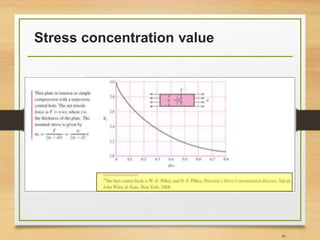
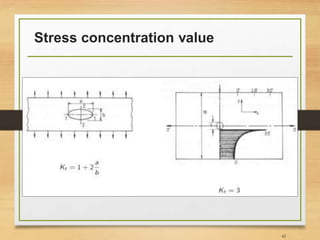
Stress concentration value 42
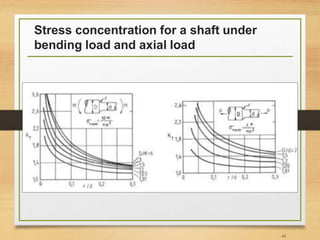
Stress concentration for a shaft under bending load and axial load 43
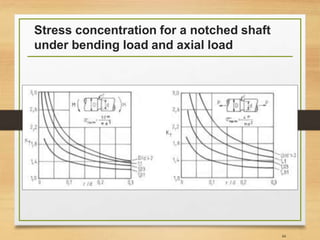
Stress concentration for a notched shaft under bending load and axial load 44
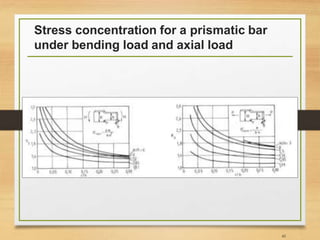
Stress concentration for a prismatic bar under bending load and axial load 45
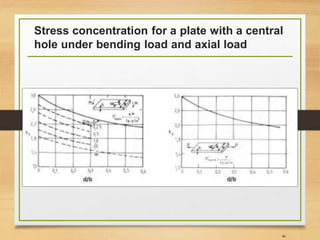
Stress concentration for a plate with a central hole under bending load and axial load 46
Fatigue Stress Concentration Factor 47 Fatigue stress concentration factor Notch sensitivity 10  q In analysis or design work, find Kt first, from the geometry of the part. Then specify the material, find q, and solve for Kf from the equation
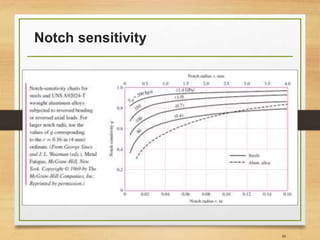
Notch sensitivity 48
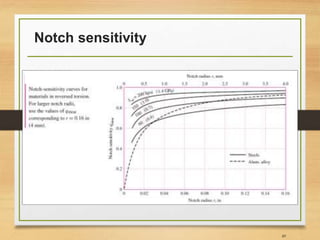
Notch sensitivity 49
Note • In using these charts it is well to know that the actual test results from which the curves were derived exhibit a large amount of scatter • It is always safe to use Kf = Kt if there is any doubt about the true value of q • Often q is not far from unity for large notch radii 50
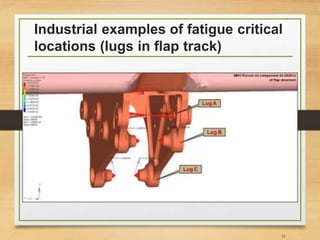
Industrial examples of fatigue critical locations (lugs in flap track) 51
Industrial examples of fatigue critical locations (fillets in flap track) 52 Fillet A
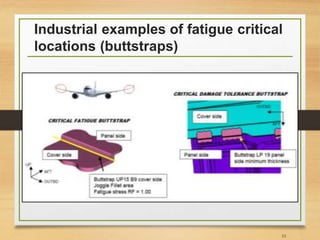
Industrial examples of fatigue critical locations (buttstraps) 53
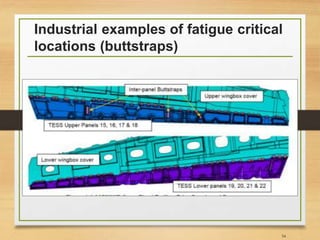
Industrial examples of fatigue critical locations (buttstraps) 54
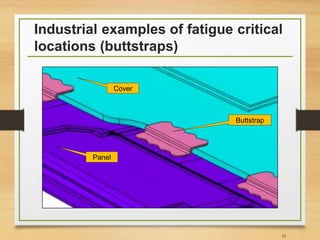
Industrial examples of fatigue critical locations (buttstraps) 55 Cover Panel Buttstrap
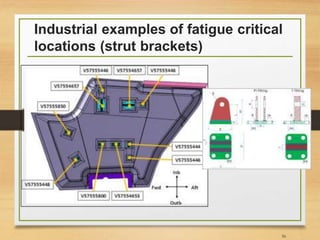
Industrial examples of fatigue critical locations (strut brackets) 56
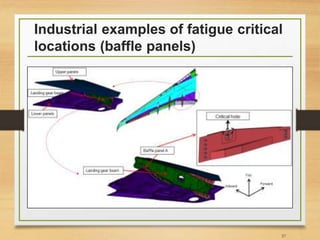
Industrial examples of fatigue critical locations (baffle panels) 57
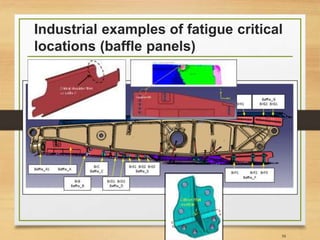
Industrial examples of fatigue critical locations (baffle panels) 58
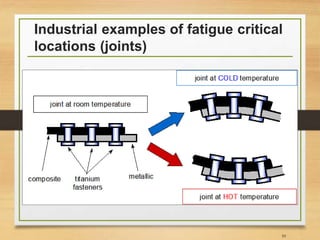
Industrial examples of fatigue critical locations (joints) 59
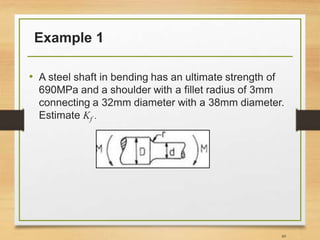
Example 1 • A steel shaft in bending has an ultimate strength of 690MPa and a shoulder with a fillet radius of 3mm connecting a 32mm diameter with a 38mm diameter. Estimate Kf . 60
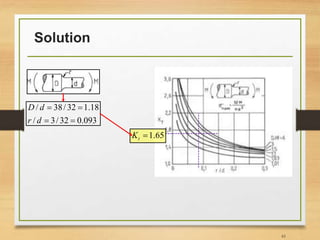
Solution 61 093.032/3/ 18.132/38/   dr dD 65.1tK
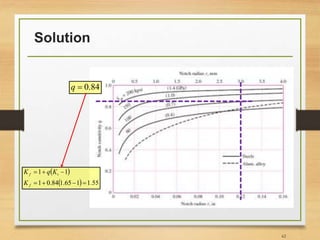
Solution 62 84.0q     55.1165.184.01 11   f tf K KqK
Example 2 • A plate with thickness h=4 mm is subjected to an alternating load P. The plate is subjected to a load cycle Pmin=10 kN and Pmax=80 kN. Considering the notch sensitivity factor of q = 0.9 calculate the life of panel. Assume a=1600 MPa and b=-0.2 and material ultimate strength is 600 MPa. 63
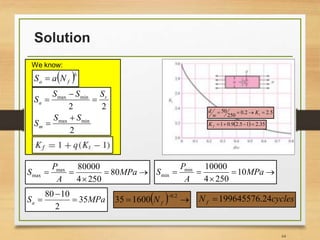
Solution 64 We know:  b fa NaS  2 22 minmax minmax SS S SSS S m r a         MPa A P S 80 2504 80000max max    MPa A P S 10 2504 10000min min MPaSa 35 2 1080    5.22.0 250 50  tK w d   35.215.29.01 fK     2.0 160035 fN cyclesN f 24.199645576
Solution • Solve the same question assuming that the hole exists on a plate with infinite length and width • What is the difference between this situation and previous situation? 65
Example 3 • Calculate maximum and minimum stresses and the load ratios for the following set of cycles, expressed as a stress range and mean stress. 66 20 30 25 12.5 33 11.5 11 29.5 60 20 90 25 )(ksiS )(ksiSm
Solution • Let’s calculate for one entry only; 67  max min minmax , S S RSSS 20 40 0 25 -5 28 24 35 -10 50 -20 70 )(min ksiS )(max ksiS   RSRSSS 1maxmaxmax  R SS   1max    2 , minmax minmax SS SSSS m       minmax maxmin 2 SSS SSS m  minmin2 SSSSm  min22 SSSm min5.0 SSSm  ksiS 20205.030min  ksiSSS 402020minmax 
Example 4 • Use the following equation to calculate the number of cycles to failure for the maximum stress and load ratios calculated in Example 3. Note that the equation is for Aluminium 2024-T3 material for Kt=1. 68   52.0 max 1log09.983.20log RSN 
Solution • Let’s calculate for one entry only; 69 20 40 0.5 48998554 0 25 0.0 132655518 -5 28 -0.18 21779524 24 35 0.69 1480700983 -10 50 -0.2 102823 -20 70 -0.29 3485 )(min ksiS )(max ksiS R fN 4899855410 52.0 40 20 140log09.983.20                 N
Tutorial 1 • A rotating shaft simply supported in ball bearings at A and D and loaded by a nonrotating force F of 6.8 kN. Estimate the life of the part assuming; • All shoulder fillets have radius of 3mm • Sut = 690MPa and Sy = 580MPa (ultimate and yield strength) • Se = 236MPa (endurance limit) • q=0.84 • a=1437MPa • b=-0.1308 70
Solution for Tutorial 1 • The first task is to see where the fatigue failure could potentially happen • We know fatigue usually happens at discontinuity, notches, fillets etc where stress is high • In this problem potential places are points B and C • So we investigate these locations 71
Solution for Tutorial 1 72   ?11_  tBf KqK ?_ BtK     55.1165.184.01 11_   tBf KqK We solved this in previous example, see below
Solution for Tutorial 1 • Let’s calculate fatigue stress concentration at point C, too. 73 086.035/3/ 08.135/38/   dr dD 6.1_ CtK
Solution for Tutorial 1 74 84.0q     5.116.184.01 11 _ _   Cf tCf K KqK
Solution for Tutorial 1 75 kNR 78.28.6 550 225 1  kNR 02.478.28.62  ).(5.69525078.2 mNMB  )(10217.3 32/3232/ 33 33 max mm d y ICB    MPa C M KS B BfB 1.33510 217.3 5.695 55.1 6 _   MPa C M KS C CfC 1.17910 209.4 5.502 50.1 6 _   Based on these stresses where does fatigue likely to happen? )(10209.4 32/3532/ 33 33 max mm d y ICC    Based on these stresses where does fatigue likely to happen? ).(5.50212502.4 mNMB 
Solution for Tutorial 1 76 MPa C M KS B BfB 1.33510 217.3 5.695 55.1 6 _   MPa C M KS C CfC 1.17910 209.4 5.502 50.1 6 _   Based on these stresses where does fatigue likely to happen? These stresses are both greater than endurance limit of 236MPa and yield stress of 580MPa. What does this mean? We have finite life and material does not yield
Solution for Tutorial 1 77    b fa NaS        b a f a S N 1 )(68000 1437 1.335 1308.0 1 cyclesN f        
Tutorial 2 (real industrial problem) • Flap track of an aircraft undergoes 414 occurrences of cyclic loading that brings about stresses at fillet locations. Stresses are obtained from detailed finite element analysis for unit load cases as shown in the next slide. Fatigue life of component follows the relationship in which A=10.7, B=3.81, C=10 and It can be further assumed that minimum stresses are zero and KDF=0.651 (knock down factor due to surface treatment). Note that above equations are in ksi units. Calculate the life of component assuming that the fatigue load on flap is 8841.8 N 78  CSBAN eqf  loglog   max minmax ,1 S S RR KDF S S D eq 
Tutorial 2 (real industrial problem) 79 Note: Stresses are in MPa and obtained for flap load of 1000N (unit load)
Solution for Tutorial 2 80 • Note that max stress need to be adjusted based on surface treatment • In this example we did not need to use Kf as we are directly extracting max stresses from detailed FEA 0 1458.8841 1000 4.16 0 max min        R MPaS S   ksiSMPaS eq D eq 3.32 89.6 7.222 7.22201 651.0 0.145        CSBA feqf eq NCSBAN log 10loglog   cyclesN f 83.36555910 103.32log81.37.10  
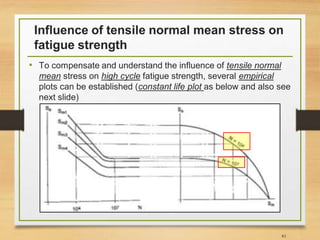
Important Notes [3] • Fatigue damage of components correlates strongly with; • Applied stress amplitude/range • Applied mean stress (mostly in high cycle fatigue region) • In high cycle fatigue, direct (normal) mean stress is responsible for opening and closing micro-cracks • Normal tensile mean stresses are detrimental and compressive mean stress are beneficial for fatigue strength (why?) • Shear mean stress has little effect on crack propagation • There is no/little effect of mean stress in low cycle fatigue due to large amount of plastic deformation 81
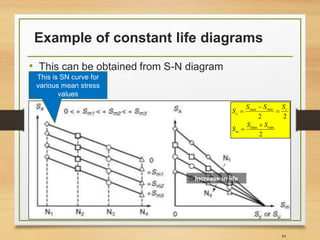
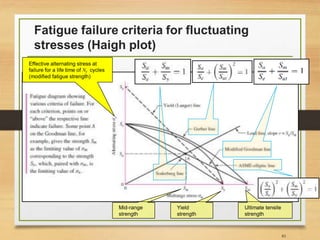
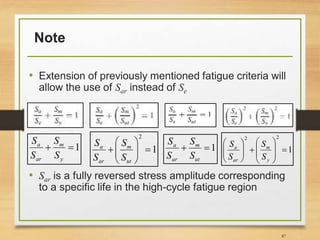
Important Notes [3] • So far, what we have been doing was based on not taking into account the effects of tensile normal mean stresses on the high cycle fatigue strength of components • We have been assuming Sm=0 • Therefore, below scientists proposed empirical equations to take such effect into account; • Gerber (1874) • Goodman (1899) • Haigh (1917) • Soderberg (1930) 82
Influence of tensile normal mean stress on fatigue strength • To compensate and understand the influence of tensile normal mean stress on high cycle fatigue strength, several empirical plots can be established (constant life plot as below and also see next slide) 83
Example of constant life diagrams 84 • This can be obtained from S-N diagram Increase in life 2 22 minmax minmax SS S SSS S m r a      This is SN curve for various mean stress values
Fatigue failure criteria for fluctuating stresses (Haigh plot) 85 Mid-range strength Yield strength Ultimate tensile strength Effective alternating stress at failure for a life time of Nf cycles (modified fatigue strength)
Note 86 Safe Unsafe Infinite life
Note • Extension of previously mentioned fatigue criteria will allow the use of Sar instead of Se • Sar is a fully reversed stress amplitude corresponding to a specific life in the high-cycle fatigue region 87 1 y m ar a S S S S 1 2        ut m ar a S S S S 1 ut m ar a S S S S 1 22                y m ar a S S S S
General observations 88 Most actual test data tend to fall between the Goodman and Gerber curves For most fatigue situations R<1 ( i.e. small mean stress in relation to alternating stress), there is little difference in the theories In the range where the theories show large differences (i.e. R values approaching 1) there is little experimental data The Soderberg line is very conservative and seldom used
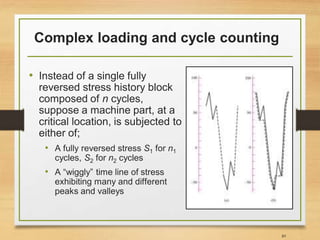
Complex loading and cycle counting • Instead of a single fully reversed stress history block composed of n cycles, suppose a machine part, at a critical location, is subjected to either of; • A fully reversed stress S1 for n1 cycles, S2 for n2 cycles • A “wiggly” time line of stress exhibiting many and different peaks and valleys 89
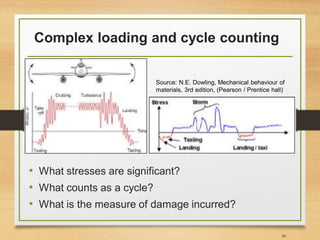
Complex loading and cycle counting 90 Source: N.E. Dowling, Mechanical behaviour of materials, 3rd edition, (Pearson / Prentice hall) • What stresses are significant? • What counts as a cycle? • What is the measure of damage incurred?
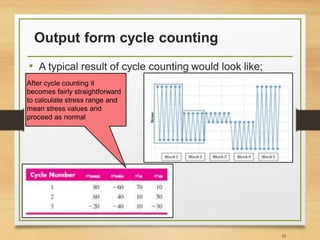
Methods of cycle counting • Beyond the scope of this lecture • Interested readers are recommended to refer to chapter 3 of Ref. [3]; • Level crossing cycle counting • Peak-valley cycle counting • Range counting • Three-point cycle counting method • Four-point cycle counting method • Rain-flow counting technique 91
Output form cycle counting • A typical result of cycle counting would look like; 92 After cycle counting it becomes fairly straightforward to calculate stress range and mean stress values and proceed as normal
Cumulative damage • Palmgren-Miner cycle-ratio summation rule (1924), also called Miner’s rule • where ni is the number of cycles at stress level Si and Ni is the number of cycles to failure at stress level Si • The parameter D has been determined by experiment • Usually 0.7<D<2.2 with an average value near unity 93
Cumulative damage 94
Note on cumulative damage • Damage parameter (D), that is defined in previous slide, is the ratio of instantaneous to critical crack length, i.e. D = a / af • There are other damage models in the literature that are not linear such as those proposed by Subramanyan (1976) and Hashin (1980) as below; 95
Example 3 • A structural member is to be subjected to a series of cyclic loads which produce different levels of alternating stress as shown in table below. Determine whether or not a fatigue failure is probable. 96
Solution • We use miner’s cumulative damage theory as below; 97   i i N n D  4 4 3 3 2 2 1 1 N n N n N n N n D 139.0 1012 10 1024 10 10 10 105 10 7 7 7 6 6 5 4 4       D
Example 4 • Calculate the total number of repetitions required for the loading of example 4 to reach the fatigue failure point. 98
Solution 99   iD 0.1 sRepetition 56.2 39.0 0.1 sRepetition
Example 5 • For the question of Tutorial 2 calculate damage for the following cases; • Damage calculation for single occurrence at each cycle • Damage calculation for all occurrences at each cycle • Damage calculation for 15000 hours (3000 hours per block) 100