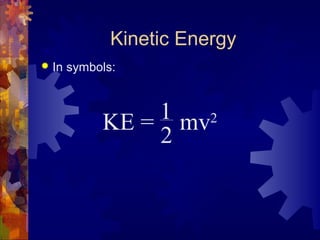
This document discusses concepts related to kinetic energy, work, potential energy, and machines. It defines kinetic energy as the energy of motion, and states that an object's kinetic energy depends on its mass and speed. Kinetic energy is calculated using the formula KE=1/2mv^2. Work is done when an object's kinetic energy changes, and work depends on the applied force and distance moved. Potential energy is stored energy due to an object's position or arrangement, such as gravitational potential energy calculated as mgh. Mechanical advantage measures how machines multiply force, while efficiency indicates the percentage of energy input that does useful work.

1. Aya Sharaireh
9 A
JUBILEE

2. Kinetic Energy
 If an object is moving, it has energy.
(Be careful, the converse of this
statement is not always true!)
 This energy is called kinetic energy -
the energy of motion.

3. Kinetic Energy
 An object’s kinetic energy depends on:
 the object’s mass.
 Kinetic energy is directly proportional to
mass.
 the object’s speed.
 Kinetic energy is directly proportional to
the square of the object’s speed.

4. Kinetic Energy
 In symbols:
KE = 1
2
mv2

5. Kinetic Energy
Kinetic energy is a scalar quantity.
Common units of kinetic energy:
Joules
An object with mass of 1 kg, moving
at 1 m/s, has a kinetic energy of 0.5
Joule.

6. Work
When the kinetic energy of an
object changes, work has been
done on the object.
Units of work: Joules
Work is a scalar quantity.

7. Work
 Work depends on:
 The amount of force applied to the object.
 The distance that the object moves while
the force is applied.
 The direction of the force with respect to
the direction the object moves.

8. Work
 If the force on the object is in the
direction the object moves, the work
done is:
W = Fx
F
x

9. Work
 If the direction of the force is opposite
the direction the object moves, work is:
W = -Fx
F
x

10. Force is NOT Work
 If the force is perpendicular to the
direction the object moves, the work
done is 0.
 If the object doesn’t move, the work
done is 0.
F
x
W = 0

11. Work and Kinetic Energy
 The work done on an object by the net
force equals the object’s change in
kinetic energy.
Wnet = ∆KE

12. Potential Energy
 Sometimes work is not converted
directly into kinetic energy. Instead it is
“stored”, or “hidden”.
 Potential energy is stored energy or
stored work.

13. Potential Energy
 Potential energy is energy that an
object (system) has due to its position
or arrangement.

14. Calculating Potential Energy
 To calculate the potential energy of a
particular arrangement:
1. Pick a position or arrangement that
you want to call the “potential energy
= 0” situation.

15. Calculating Potential Energy
2. The potential energy of any other
position or arrangement equals the
negative of the work that the
conservative force does in changing
from the potential energy = 0 situation
to that one.
PE = - WorkF

16. Conservative Forces
 Energy or work is stored when a force
does work “against” a force such as the
gravitational force or a Hooke’s Law
(spring) force.
 Forces that store or hide energy are
called conservative forces.

17. Gravitational PE
 The gravitational potential energy of an
object at height h equals the negative of
the work that gravity does when the
object is lifted from the PE = 0 position.
GPE = mgh

18. Mechanical Energy
 Mechanical Energy = PE + KE

19. Conservation of Energy
 If no external forces act on a system,
the total energy of the system will
remain constant.

20. Power
 Power is the rate work is done.
Power =
∆Work
time
W
P t

21. Power
 Units of power: 1 Joule/sec = 1 Watt
 1000 Watts = 1 kilowatt
 Power is a scalar quantity.

22. (Simple) Machines
 A machine is a mechanical device used
to do work.
 Examples of simple machines:
 Inclined plane
 Lever
 pulley

23. (Simple) Machines
 A machine can never output more work
(energy) than is put into it.
 At best,
Workout = Workin
Machine
Workin
Workout

24. Mechanical Advantage
 Machines can’t multiply work or energy,
but they can multiply force. Mechanical
advantage measures how much a
machine multiplies force.
MA =
Force machine exerts
Force you exert

25. Efficiency
 The efficiency of a machine tells how
much of the energy (work) that goes
into the machine actually does useful
work.
 It is usually expressed as a percent.
Efficiency =
Useful work done
Energy input
x 100%

26. The End