The document discusses various physics concepts related to work, energy and power including: - The definition of work in physics and the formula to calculate work. - Kinetic energy and its formula. Kinetic energy depends on an object's mass and velocity. - Gravitational potential energy and its formula. Gravitational potential energy depends on an object's mass, height above ground, and gravitational acceleration. 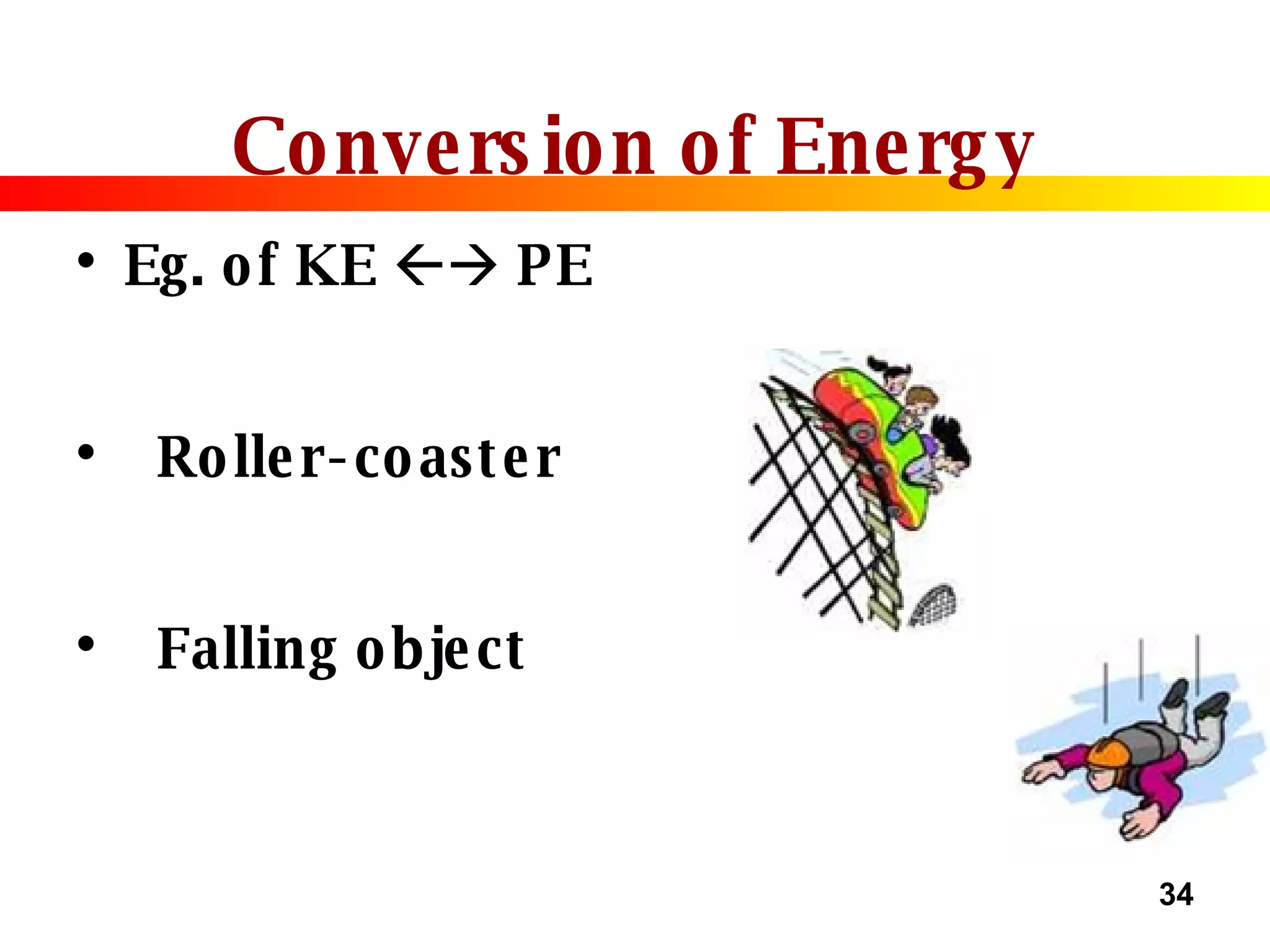- The principles of conservation and conversion of energy. Energy cannot be created or destroyed, it can only change form.

1. Work, Energy & Power Sec 3 Exp/NA

2. Specific Instructional Objectives At the end of the lesson, students should be able to: Show understanding of the Physics concept of Work Correctly identify Work from given situations Recall and show understanding of the formula to calculate work done Solve related problems involving work

3. Work What does WORK mean to you? Are you doing WORK when… Lifting weights? Walking with a big bag of grocery in your hand? Completing your homework assignment? Writing an essay?

4. Physics concept of WORK WORK is done only when a constant force applied on an object, causes the object to move in the same direction as the force applied.

5. Physics concept of WORK What IS considered as work done in Physics: You push a heavy shopping trolley for 10 m You lift your school bags upwards by 1 m

6. Physics concept of WORK What is NOT considered as work done: You push against a wall Jumping continuously on the same spot Holding a chair and walking around the classroom

7. Physics concept of WORK WORK can be calculated by: Work done = Constant x Distance moved force (N) in the direction of force (m) W = F x s Units: [J] [N] [m] SI Unit for Work is JOULE (J)

8. More Examples of WORK You are helping to push your mother’s heavy shopping cart with a force of 50 N for 200 m. What is amount of work done? Work done, W = F x s = 50 x 200 = 10,000 J or 10 kJ (kilo-Joules)

9. More Examples of WORK: Jack put on his bag-pack of weight 120 N. He then starts running on level ground for 100 m before he started to climb up a ladder up a height of 10 m. How much work was done? From Physics point of view, no work is done on pack at level ground. Reason: Lift is perpendicular to movement. Work is done on pack only when Jack climbs up the ladder. Work done, W = F x s = 120 x 10 = 1200 J or 1.2 kJ

10. Specific Instructional Objectives At the end of the lesson, students should be able to: Show understanding of the Physics concept of Kinetic Energy (KE) Recall and show understanding of the formula Distinguish situations involving KE Solve related problems involving KE

11. Energy – Quick Re-cap Energy is the capacity to do work SI Unit: Joule (J) Many forms Common ones: Kinetic Potential Electric Chemical Solar Nuclear

12. Kinetic Energy (KE) A form of energy that a body in motion possess. A body a rest, will it possess any KE? Examples: Bullet shot out from pistol Helicopter flying at 120km/h

13. Kinetic Energy (KE) The amount of KE of a moving body depends on: Mass of body (kg) Velocity (ms -1 ) When either mass or velocity of moving body is increased, KE will also increase.

14. Kinetic Energy (KE) Formula: SI Unit: Joule [ J ] … same as Work Done Kinetic Energy = x Mass x (Velocity) 2 KE = x m x v 2 Units: [ J ] [kg] [ms -1 ] 2

15. Kinetic Energy (KE) KE = ½  m  v 2 Mass = m kg Velocity, V

16. Examples of KE Find the KE of an empty van of mass 1000kg moving at 2m/s. Find the KE of van when it is loaded with goods to give a total mass of 2000kg, and moving at 2m/s. Find KE of unloaded van when it speeds up to 4m/s. KE of van at 2m/s = ½ x 1000 x (2) 2 = 2000 J = 2 kJ KE of van at 2m/s = ½ x 2000 x (2) 2 = 4000 J = 4 kJ KE of van at 2m/s = ½ x 1000 x (4) 2 = 8000 J = 8 kJ

17. Kinetic Energy (KE) Formula: KE = ½ mv 2 From the formula, what can you infer about the change in KE when… Mass doubles Velocity doubles KE doubles KE increases by FOUR times

18. Examples of KE A motorcycle accelerates at 2m/s 2 from rest for 5s. Find the KE of motorcycle after 5s. Mass of motorcycle is 200 kg. Velocity of motorcycle after 5s, a = (v-u) t v = 2(5) + 0 = 10m/s KE of motorcycle at 10m/s = ½ x 200 x (10) 2 = 10,000 J = 10 kJ

19. Specific Instructional Objectives At the end of the lesson, students should be able to: Show understanding of the Physics concept of Gravitational Potential Energy Recall and understand the formula Distinguish situations involving GPE Solve related problems involving GPE

20. Potential Energy Potential energy is the energy possessed by an object as a result of its POSITION or CONDITION . Two common kinds: Gravitational PE Elastic PE (not in syllabus)

21. Elastic PE Energy that can be possessed by an object due to its CONDITION. Examples: “ Slinky” … when stretched or compressed Spring … when stretched or compressed Rubber band … when stretched Balloon with air … when compressed

22. Gravitational PE Energy that can be possessed by an object due to its POSITION . In Physics, ground level is normally assumed to be at ZERO GPE. Any object that is at ground level has ZERO GPE. If object is lifted a certain height above ground, its GPE has increased.

23. Gravitational PE Examples: When a chair lifted from ground a distance of 1m You sitting on the 3 rd storey of this building

24. Gravitational PE Can be calculated with: GPE = mass  gravitational  height above acceleration ground level = m  g  h Units: [J] [kg] [m/s 2 ] [m] SI Units of GPE : Joule [J] Ground, 0 GPE Distance from ground, h Object on top of building, of mass, m g earth

25. Example of GPE You lifted your bags to the top of your table. What can you say about the GPE of your bag? Zero, increase, decrease Lift the same bag on the Moon. What happens to GPE? Zero, increase, decrease Will the GPE be the same on Earth and Moon? Same, less on Moon, more on Moon?

26. Examples of GPE You lifted a set of books of mass 3kg, for 2m. What is the GPE gained by the books? Take g=10m/s 2 . Find the work done by you to lift the books. GPE = mgh = 3  10  2 = 60 J Work done, W = F  d (F = weight of books) = (m  g)  d = 3 x 10 x 2 = 60 J (Note: same as GPE)

27. Conservation & Conversion of Energy

28. Specific Instructional Objectives At the end of the lesson, students should be able to: Show understanding of conservation & conversion of energy Correctly distinguish situation involving energy conservation & conversion Solve related problems

29. Specific Instructional Objectives At the end of the lesson, students should be able to: Show understanding of conservation & conversion of energy Correctly distinguish situation involving energy conservation & conversion Solve related problems

30. Energy of an object can be thought of as the sands in an hourglass! Energy always remain same or fixed in quantity! But this sand can change position, from the top to bottom and bottom to top! Likewise energy can change in form eg. From KE  PE Conservation of Energy

31. Conservation of Energy Note that energy CANNOT be created nor destroyed! So what does this mean when viewed in context of the Earth?

32. Conservation of Energy Conversion of energy is the term used to denote change in energy from one form to another. Eg. Burning candle: Chemical  Heat, Light Fuel: Chemical  Heat  KE  Electricity Nuclear explosion: Nuclear  Heat, light Spring: Elastic PE  KE

33. Conversion of Energy For O-Levels, we are only concerned with: KE  GPE And such situations are only found when a moving object is at the same time undergoing changes in height

34. Conversion of Energy Eg. of KE  PE Roller-coaster Falling object

35. Free Falling object model An object in free fall means the object is falling freely, under the influence of gravity When the object is at the highest position , the GPE is at maximum and KE is zero . When the object is falling , the GPE decreases as it loses height, and the KE increases At the lowest position , the KE is at maximum and GPE is zero .

36. A fresh durian of mass 5 kg is found growing at the end of a tree branch 20 m above ground. When ripe, the durian will by itself drops to the ground below. Let gravity = 10m/s 2 . Find the energy of the fresh durian? What form is it? GPE. GPE = mgh = 5 x 10 x 20 = 1000J Find the GPE and KE of the durian when it is 5m above ground. Sum up both the GPE and KE and compare the value with above. What can you infer from the results? GPE = 5 x 10 x 5 = 250J. s = ½ vt, v = gt s = ½ gt 2 , t = sqrt 3 KE = ½ mv 2 = ½ (5)(10sqrt3) 2 = 750J v = 10(sqrt 3) Sum of energies = 250 + 750 = 1000J Same as above => energy is conserved. Eg. of Conservation of Energy

37. Eg. of Conversion of Energy A car of 800 kg is moving at an average speed of 5 m/s. The traffic light changed to red and so the driver stepped on the brakes to bring the car to a quick, sudden and screeching halt. Find energy of moving car and what form of energy is this? KE. KE = ½ mv 2 = ½ x 800 x 5 2 = 10,000 J. What energy does the car possesses when it stops? None. What happened to the original energy of the moving car? KE has changed to Sound and Heat Energy.