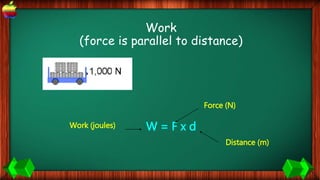
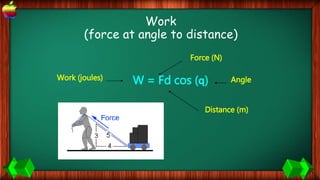
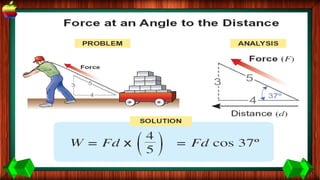
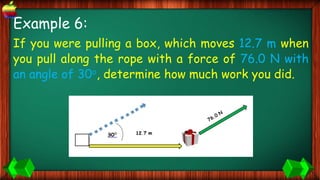
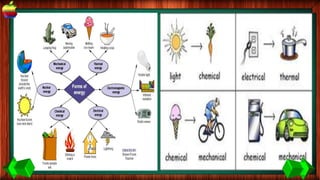
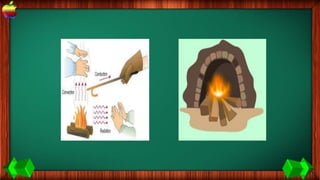
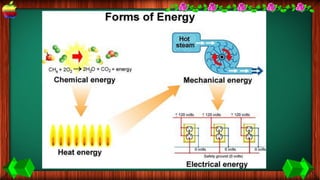
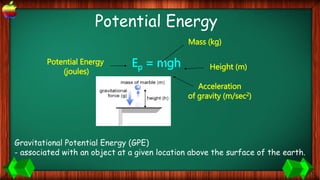
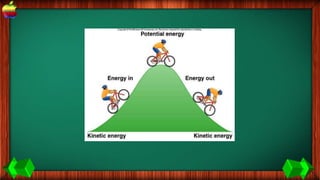
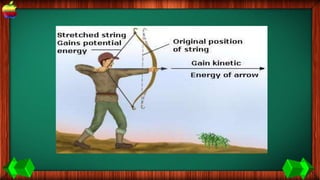
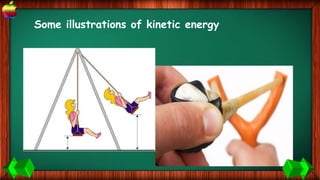
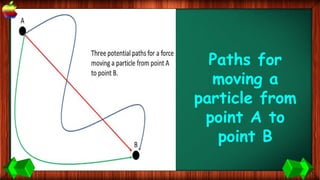
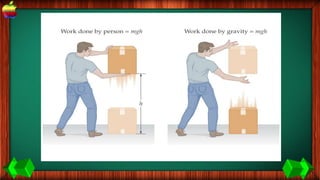
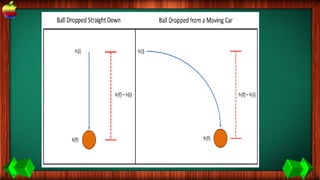
This document provides information about work, energy, and the different types of energy. It begins with definitions of work and discusses how work is calculated based on force and distance. It then defines different types of energy including kinetic energy, potential energy, heat energy, chemical energy, electromagnetic energy, and nuclear energy. Examples are provided to demonstrate how to calculate work, kinetic energy, and potential energy. The last sections discuss conservative and non-conservative forces and how the law of conservation of energy applies.

1. EnergyWork &
Click Here To Start
Dr. Merced GutierrezSubmitted To:

2. Work &
Energy
Sultiz, Larry J.
Group 1
Leader:
Member
s:
Cheryl Mae O. Mabuting Dianara M. PalermoApril Rose C. Torrejas Regine L. Lacaza

3. Work
Sultiz, Larry J.

4. Work
In physics, work represents
a measurable change in a
system, caused by a force.

5. If you push a box with a force of one newton for a
distance of one meter, you have done exactly one joule
of work.
Work

6. Work
(force is parallel to distance)
W = F x d
Distance (m)
Force (N)
Work (joules)

7. Example 1:
I am holding a 2 kg block of cheese in
my hands. I walk 12 m to the other side
of the room.
Explain if I did any work.

8. Example 2:
I decide to do a little weight lifting
(but I’m going to start off slow!). I lift
10 kg from the floor, over my head, and
back down to the floor.
Explain if I did any work.

9. Example 3:
Last winter my car got caught in a snow
bank. I promise one of my friends that if
he comes over to do some work for me I’ll
buy him pizza. We get behind the car and
push it out of the snow.
Explain if I did any work.

10. Example 4:
I am holding a 10kg book in my hand. I put it
down on the floor. Explain if we did any work.
Explain if I did any work.

11. Example 5:
My nephew Lanz Gabriel, grabs my
other nephew Zendric’s leg and drags him
2.3 m across the floor. If he exerted a
force of 8.1 N to do this, determine how
much work he did?
Explain if I did any work.

12. Work
(force at angle to distance)
W = Fd cos (q)
Distance (m)
Force (N)
Work (joules) Angle

14. Example 6:
If you were pulling a box, which moves 12.7 m when
you pull along the rope with a force of 76.0 N with
an angle of 300, determine how much work you did.

15. Why the path doesn't matter

16. Work
(done against gravity)
W = mgh
Height object raised (m)
Gravity (m/sec2)
Work (joules)
Mass (g)

17. Calculate work
• A crane lifts a steel beam with a
mass of 1,500 kg.
• Calculate how much work is done
against gravity if the beam is
lifted 50 meters in the air.

18. Energ
y
April Rose C. Torrejas

19. What is Energy?
 Energy is the ability to do work.
 If an object or organism does work (exerts a force
over a distance to move an object) the object or
organism uses energy.
 Because of the direct connection between energy and
work, energy is measured in the same unit as work:
joules (J).

21. Forms of Energy
The five main forms of energy are:
1.Heat
2.Chemical
3.Electromagnetic
4.Nuclear
5.Mechanical

22. Heat Energy
The internal motion of the atoms is called
heat energy, because moving particles
produce heat.
Can be produced by friction.
Causes changes in temperature and phase
of any form of matter.
Forms of Energy

24. Chemical Energy
Is required to bond atoms together
and when bonds are broken, energy is
released.
Forms of Energy

26. Electromagnetic Energy
 Power lines carry electromagnetic energy
into your home in the form of electricity.
 Light is a form of electromagnetic energy.
 Each color of light (RoyGBiv) represents a
different amount of electromagnetic energy.
Electromagnetic Energy is also carried by X-
rays, radio waves, and laser light.
Forms of Energy

28. Nuclear Energy
The nucleus of an atom is the source of
nuclear energy.
The sun’s energy is produced from a
nuclear fusion reaction in which hydrogen
nuclei fuse to form helium nuclei.
Forms of Energy

30. Mechanical Energy
When work is done to an object, it acquires
energy. The energy it acquires is known as
mechanical energy.
When you kick a football, you give mechanical
energy to the football to make it move.

33. Regine L. Lacaza
Potential Energy

34. When the work is waiting to be done, or when
there is the potential for work to be performed, we
term the energy “potential”
The unit for potential energy is: Joules or kg/m2/s2

35. Potential Energy
Ep = mgh Height (m)
Mass (kg)
Potential Energy
(joules)
Acceleration
of gravity (m/sec2)
Gravitational Potential Energy (GPE)
- associated with an object at a given location above the surface of the earth.

36. Potential Energy
A cart with a mass of 102 kg is pushed
up a ramp.
The top of the ramp is 4 meters higher
than the bottom.
How much potential energy is gained by
the cart?

38. Calculate the gravitational potential energy of a
skydiver with a mass of 80kg about to jump out of a plane
at an altitude of 5000m?
PE = m x g x h
PE = 80 x 9.8 x 5000 [remember acceleration due to
gravity = 9.8 m/s2
PE = 3920000 Joules = 3920 kilo joules (kJ)

39. A brick with a mass of 1 kg is lifted to the top
of a 4 m high roof. It slips off the roof and falls to
the ground.
Calculate the gravitational potential energy of the
brick at the top of the roof and on the ground once
it has fallen.
The mass of the brick is m = 1 kg
The height lifted is h = 4 m

40. a. We are asked to find the gain in potential energy
of the brick as it is lifted onto the roof?
Ep= mgh
=(1kg)(9.8m/𝑠2
)(4m)
=39.2 J

41. A boy has a mass of 30 kg climbs onto the roof of a
garage. The roof is 2.5 m from the ground.
1.How much potential energy did the boy gain by
climbing onto the roof?
PE= mgh
PE= (30)(9.8)(2.5)
PE= 735 J

42. The boy now jumps down. What is the potential
energy of the boy when he is 1 m from the ground?
PE= mgh
= (30kg)(9.8m/𝑠2
)(1m)
=294 J
When he is on the ground the height is 0 and so the
potential energy is 0J.

43. Elastic Potential Energy
- can be thought of as the energy stored
in the deformed spring (one that is
either compressed or stretched from its
equilibrium position).
Equation for EPE =
1
2
kx2

45. Example:
50N of force is applied to a spring having 150N/m spring
constant. Find the amount of compression of the spring.
Fspring = -kx=Fapplied
50N = - 150.x
X = -3m “-“shows the direction of compression.

47. The vertical spring is attached to the load of mass 5 kg and is
compressed by 8 m. Calculate the Force constant of the spring?
Solution:
Given: Mass m = 5kg,
Distance x = 8 cm,
Force Constant k = ?
Force is given by F = ma
= 5 kg × 9.8 m/s2
= 49 N.
Force in the stretched spring is given by F = kx
Force Constant k = Fx
= 49N8m
= 6.125 N/m.

48. An Olympic archer applies a force of 100N in pulling back
her bow by 0.5m. How much energy is stored in the bow?
Elastic PE = F x d
Elastic PE = 100 x 0.5
Elastic PE = 50 Joules
Thus 50 Joules of work was done by the archer on the bow
which will be transferred to the arrow when it is released.

49. Kinetic Energy
Cheryl Mae O. Mabuting

50. Kinetic Energy
 The work done on a body that caused the
body to be set in motion with some
speed v can be expressed as function of the
body's final speed v and mass m, independent
of type of force that acted on the body.

51. Kinetic Energy
 Kinetic energy is a scalar.
 An energy in motion.
 The kinetic energy of an object is completely
described by magnitude alone.
 The units are the same as for work (i.e.
Joules, J).

52. Kinetic Energy
Ek = 1 mv2
2
Speed (m/sec)
Mass (kg)
Kinetic Energy
(joules)

53. Kinetic Energy
The kinetic energy of a moving object depends on two
things: mass and speed.
Kinetic energy is proportional to mass.

54. Mathematically, kinetic energy increases as the square
of speed.
If the speed of an object doubles, its kinetic energy
increases four times. (mass is constant)
Kinetic Energy

55. Calculate Kinetic Energy
A car with a mass of 1,300 kg is
going straight ahead at a speed of
30 m/sec (67 mph).
Calculate:
a) The kinetic energy of the car.

56. 1.
2.

57. Note the following:
1. Both balls had potential energy as they rested on the
table.
2. By resting up on a high table, they also had gravitational
energy.
.
3. By moving and falling off the table (movement), potential
and gravitational energy changed to Kinetic Energy. Can you
guess which of the balls had more kinetic energy? (The big
and heavier ball)

58. Some illustrations of kinetic energy

59. Some illustrations on kinetic energy

60. CALCULATIONS:
 A 500 kilogram car is driving at 15 meters/second.
What's its kinetic energy?
Solution:
V= 15m/s M= 500kg
Kinetic energy = 1/2mv2(500kg)(15m/s2
KE = 56250 Joules

61. CALCULATIONS:
 Determine the kinetic energy of a 625-kg roller
coaster car that is moving with a speed of 18.3
m/s.
Solution:
KE = 0.5*m*v2
KE = (0.5) * (625 kg) * (18.3 m/s)2
KE = 1.05 x105 Joules

62. WORK-ENERGY THEOREM
 The energy associated with the work done by the
net force does not disappear after the net force
is removed (or becomes zero), it is transformed
into the Kinetic Energy of the body. We call this
the Work-Energy Theorem.
KE= ½ mv2
Wnet = ∆ KE
Wnet = KEf – KEi

63. Relation bewteen KE and W:
 The work done on an object by a net force equals
the change in kinetic energy of the object:
W = KEf - KEi.
 This relationship is called work-energy theorem

64. Potential Energy Kinetic Energy
Definition
Potential energy is due do position, composition or
arrangement.
Kinetic energy is energy due to motion.
Formula
mass of the object x acceleration of Gravity x Height of
the object, PE = m x g x h
1/2 x mass of the object x speed of the object², KE = ½ x
M x V².
S.I. Unit Joule Joule
Example Wound up spring of a toy, a stone on top of a hill, etc. A person who is walking, a pen falling from a table, etc.
Types Gravitational, Elastic and Chemical Potential Energy. Rotational and Translational Kinetic Energy.

65. CONSERVATIVE
AND
NON-CONSERVATIVE
FORCES
Dianara M. Palermo

66. CONSERVATIVE FORCES
 Forces that store energy.
 The work a conservative force does
on an object in moving it from A to B
is path independent - it depends only
on the end points of the motion.

67. Can be thought of as a force that conserves
mechanical energy.
KE(final) + GPE(final) = KE(initial) + GPE(initial)

68. Example:
Gravitational force: mechanical work against
it depends just on difference in elevation not
how an object is lifted.
Elastic force: work against spring only
depends on
length change.

69. Paths for
moving a
particle from
point A to
point B

72. NON-CONSERVATIVE FORCE
 a force that goes against any kind of
friction because of the energy it takes from
the system can't be stored.
 The work done by a non conservative force
does depend upon the path taken.

73. Example:

74. Law of Conservation of Energy
As energy takes different forms and changes things by
doing work, nature keeps perfect track of the total.
No new energy is created and no existing energy is
destroyed.

76. Thank You
For Your
Cooperation!