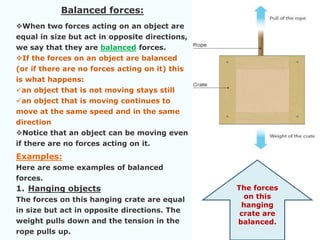
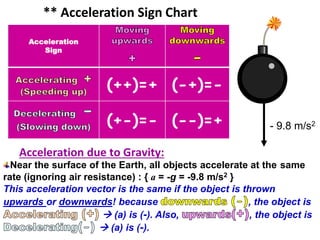
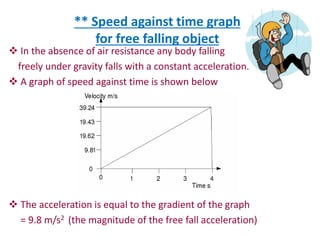
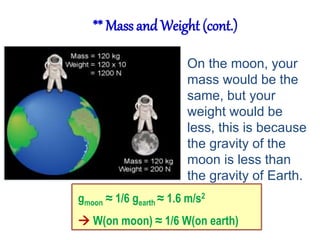
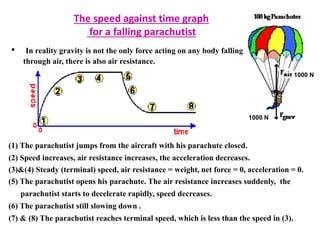
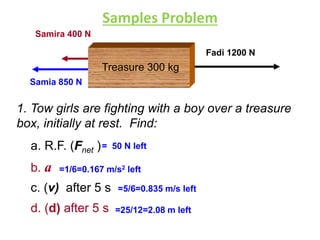
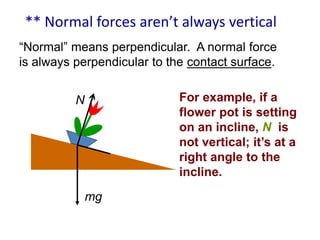
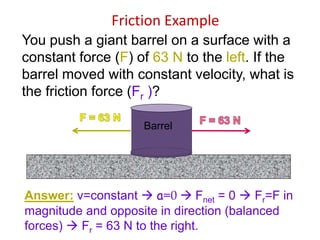
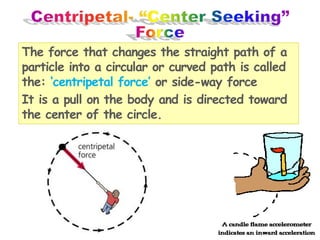
A force is any interaction that causes a change in the motion of an object. There are several key laws of motion:
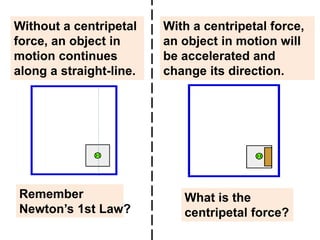
1) Newton's First Law states that an object at rest stays at rest and an object in motion stays in motion with the same speed and in the same direction unless acted upon by an unbalanced force.
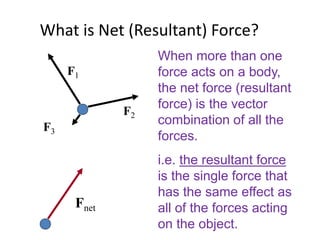
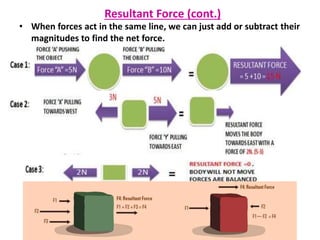
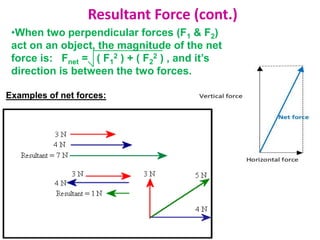
2) Newton's Second Law states that the acceleration of an object as produced by a net force is directly proportional to the magnitude of the net force, in the same direction as the net force, and inversely proportional to the mass of the object.
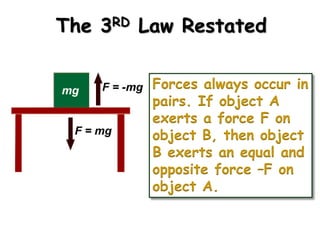
3) Newton's Third Law states that for every action, there is an equal and opposite reaction.
The document goes









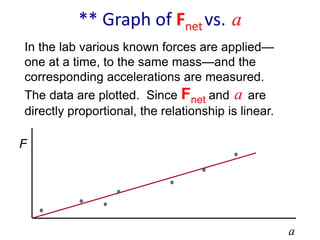
![** Mass = Slope
Since slope (rise /run) = F/ a, the slope is
equal to the mass.
F
a
so [m = F / a]
F
a](https://image.slidesharecdn.com/forceandmotion-141107155950-conversion-gate02/85/Force-and-motion-12-320.jpg)