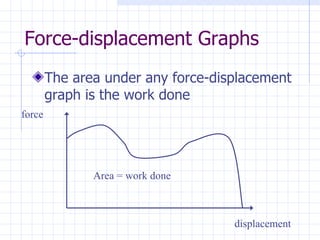
1) Work is defined as the force multiplied by the distance moved in the direction of the force. It is a scalar quantity measured in joules. 2) The area under a force-displacement graph represents the work done. 3) There are different types of energy including kinetic, potential (gravitational and elastic), chemical, and others. Energy is quantified measured in joules and is conserved in mechanical systems.

1. Mechanics
Topic 2.3 Work, Energy and Power

2. Work
A simple definition of work is the force
multiplied by the distance moved
However this does not take in to account of
the case when the force applied is not in the
direction of the motion
Here we have to calculate the component of
the force doing the work in the direction
moved
i.e. Work is equal to the magnitude of the
component of the force in the direction
moved multiplied by the distance moved

3. Work = Fs = Fs cosθ
Where
 F is the force F
 s is the displacement
 θ is the angle between the force and the
direction θ
s

4. The SI unit of work is the newton-metre
(Nm) and it is called the joule (J)
Work is a scalar quantity

5. Force-displacement Graphs
The area under any force-displacement
graph is the work done
force
Area = work done
displacement

6. Energy and Power
Kinetic Energy
 This is the energy that a body possesses
by virtue of its motion
 If the mass of a body is m and its velocity
is v then its kinetic energy, Ek = ½ m v2

7. Energy and Power
Gravitational Potential Energy
 This is the energy that a body possesses
by virtue of its position in the gravitational
field
 If the mass of a body is m and its height
above a fixed position is h then its change
in gravitational potential energy,
∆Ep = mg∆h
 where g = the acceleration due to gravity

8. The Principle of Conservation
of Energy
Energy can be transformed
from one form to another, but it
cannot be created nor
destroyed, i.e. the total energy
of a system is constant
Energy is measured in joules
and it is a scalar quantity

9. Types of Energy
Kinetic
Gravitational Potential
Elastic
Heat (often refered to as internal)
Light
Sound
Electrical
Chemical
Nuclear

10. Energy and Power
Elastic Potential Energy
 This is the energy that a body possesses
by virtue of its position from the
equilibrium condition of the spring
 If the mass of a body is m and its
displacement from the equilibrium position
is s then its elastic potential energy,
∆E elas = ½ k s2
 where k = the spring constant

11. In Mechanical Situations
Falling objects and roller coaster rides
are situations where Ep + Ek = constant
if we ignore the effects of air resistance
and friction.
Inclined planes and falling objects can
often be solved more simply using this
principle rather than the kinematics
equations

12. In all collisions and explosions momentum is
conserved, but generally there is a loss of
kinetic energy, usually to internal energy
(heat) and to a small extent to sound
In an inelastic collision there is a loss of
kinetic energy (momentum is still conserved)
In an elastic collision the kinetic energy is
conserved (as well as momentum)

13. Power
Power is the rate of working
Power = work
time
P = ∆W
∆t
The unit of power is the joule per
second (Js-1) which is called the watt
(W)

14. Power and Velocity
Since ∆W = Fs
And power developed P = ∆W
∆t
Then P = Fs
∆t
But s = velocity
∆t
Therefore P = Fv

15. Efficiency
Efficiency is defined as the ratio of the
useful output to the total input
This can be calculated using energy or
power values as long as you are
consistent
Efficiency is normally expressed as a
percentage