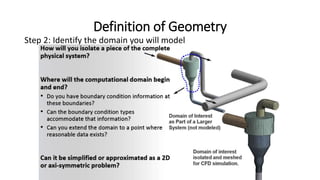
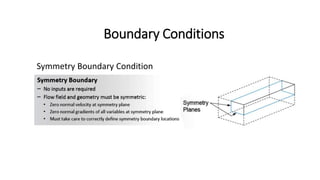
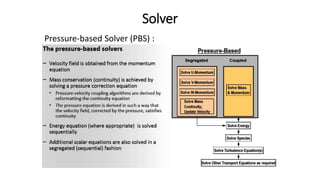
This document discusses computational fluid dynamics (CFD). CFD uses numerical analysis and algorithms to solve and analyze fluid flow problems. It can be used at various stages of engineering to study designs, develop products, optimize designs, troubleshoot issues, and aid redesign. CFD complements experimental testing by reducing costs and effort required for data acquisition. It involves discretizing the fluid domain, applying boundary conditions, solving equations for conservation of properties, and interpolating results. Turbulence models and discretization methods like finite volume are discussed. The CFD process involves pre-processing the problem, solving it, and post-processing the results.