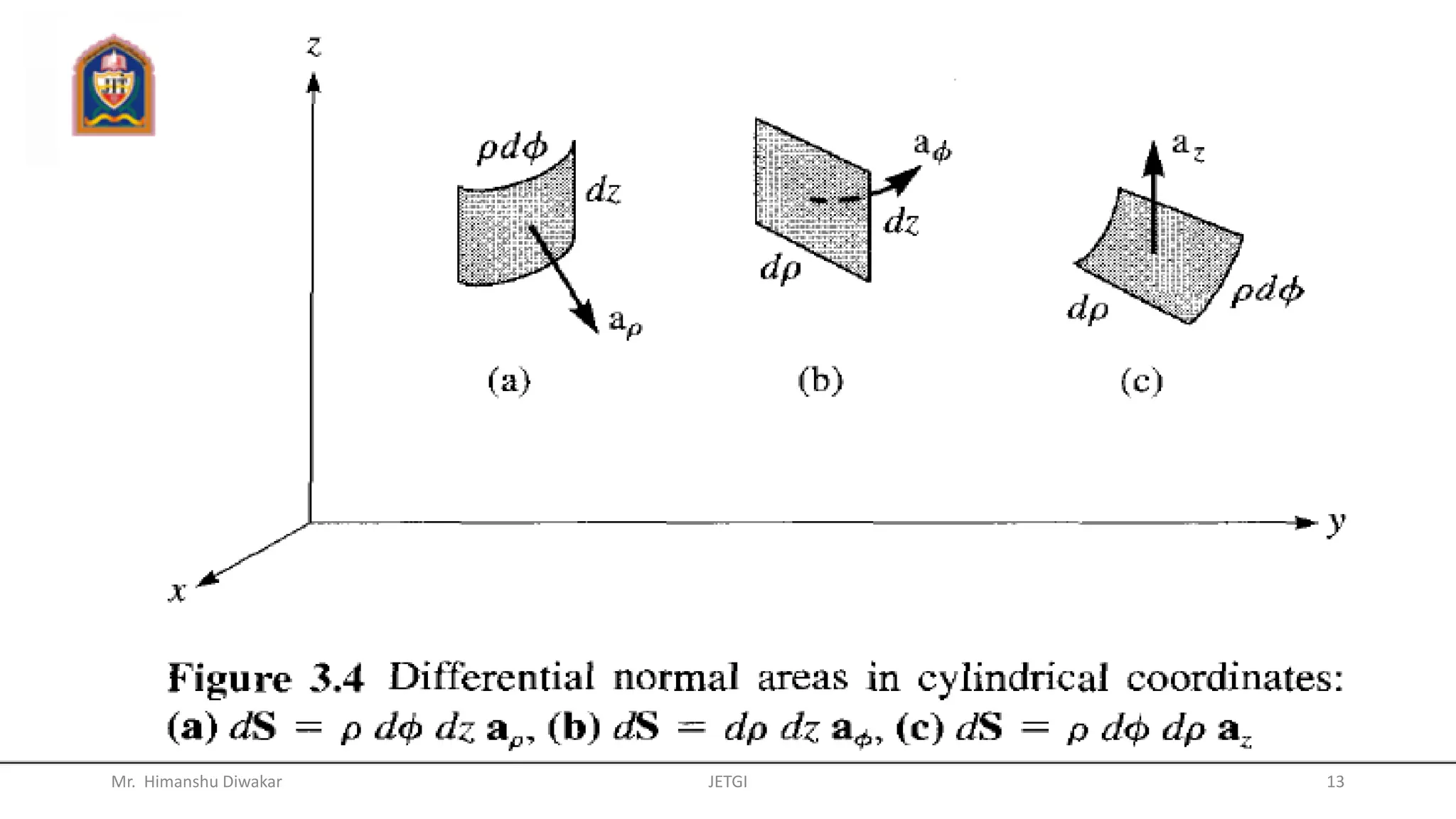
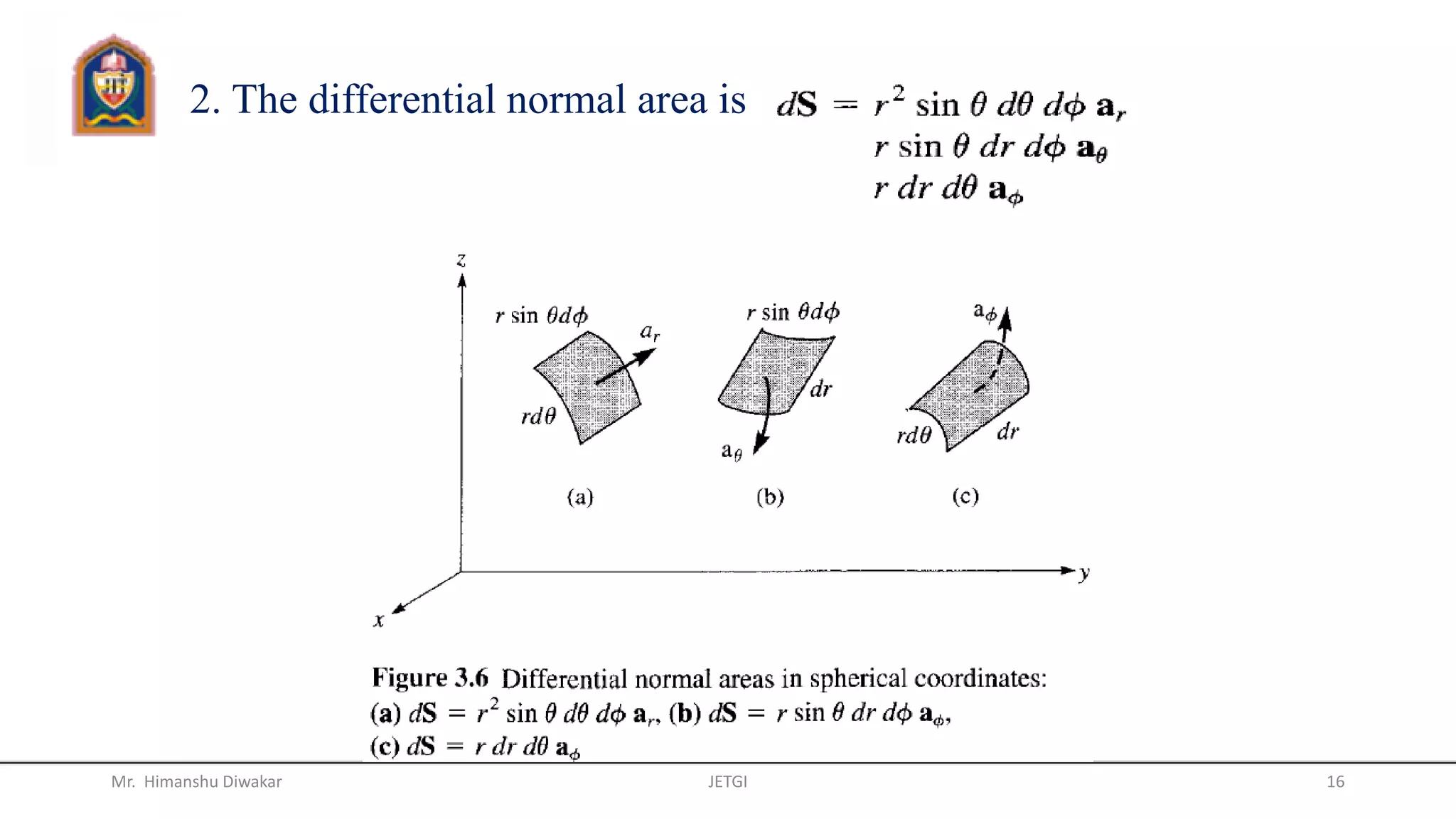
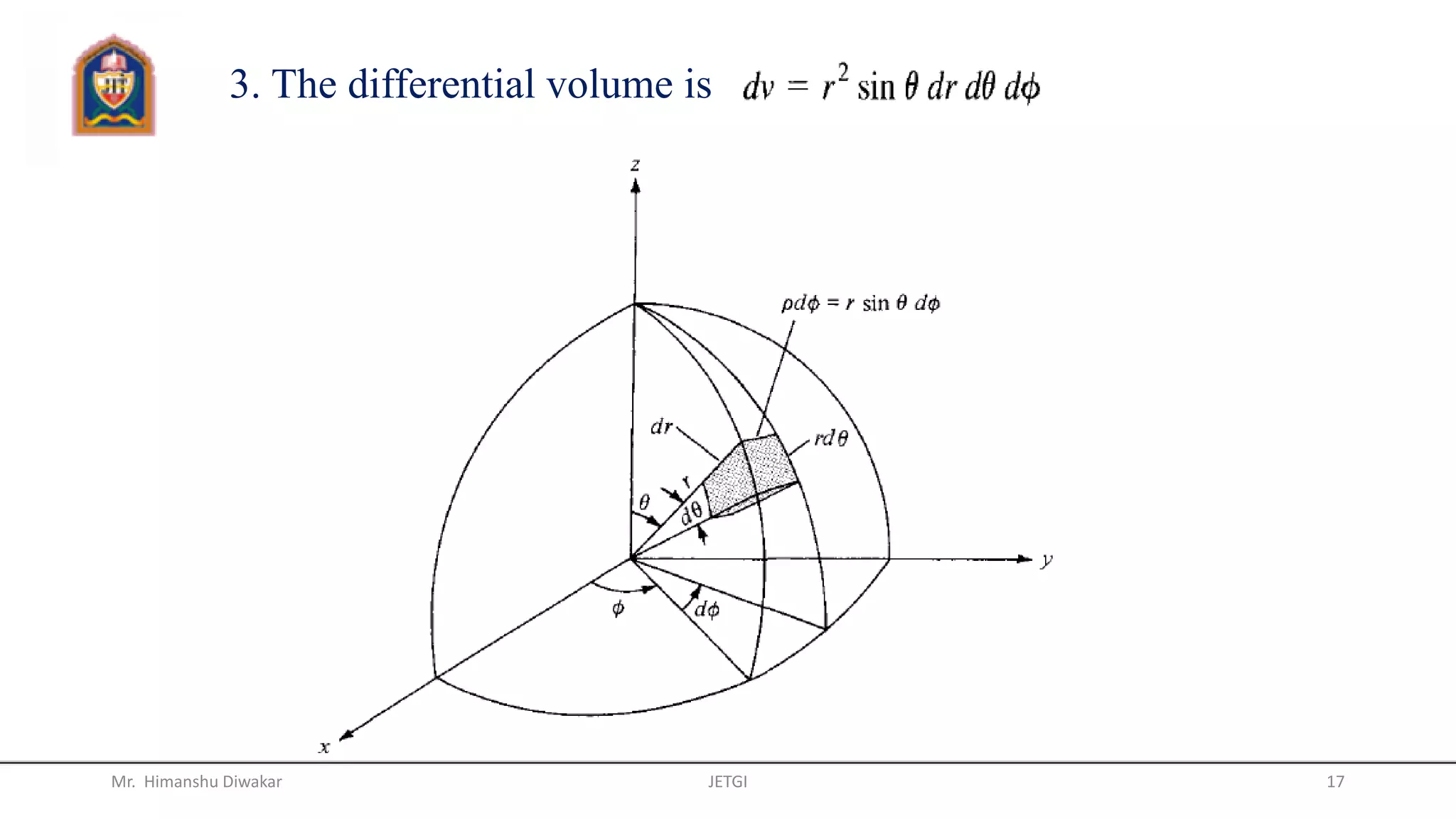
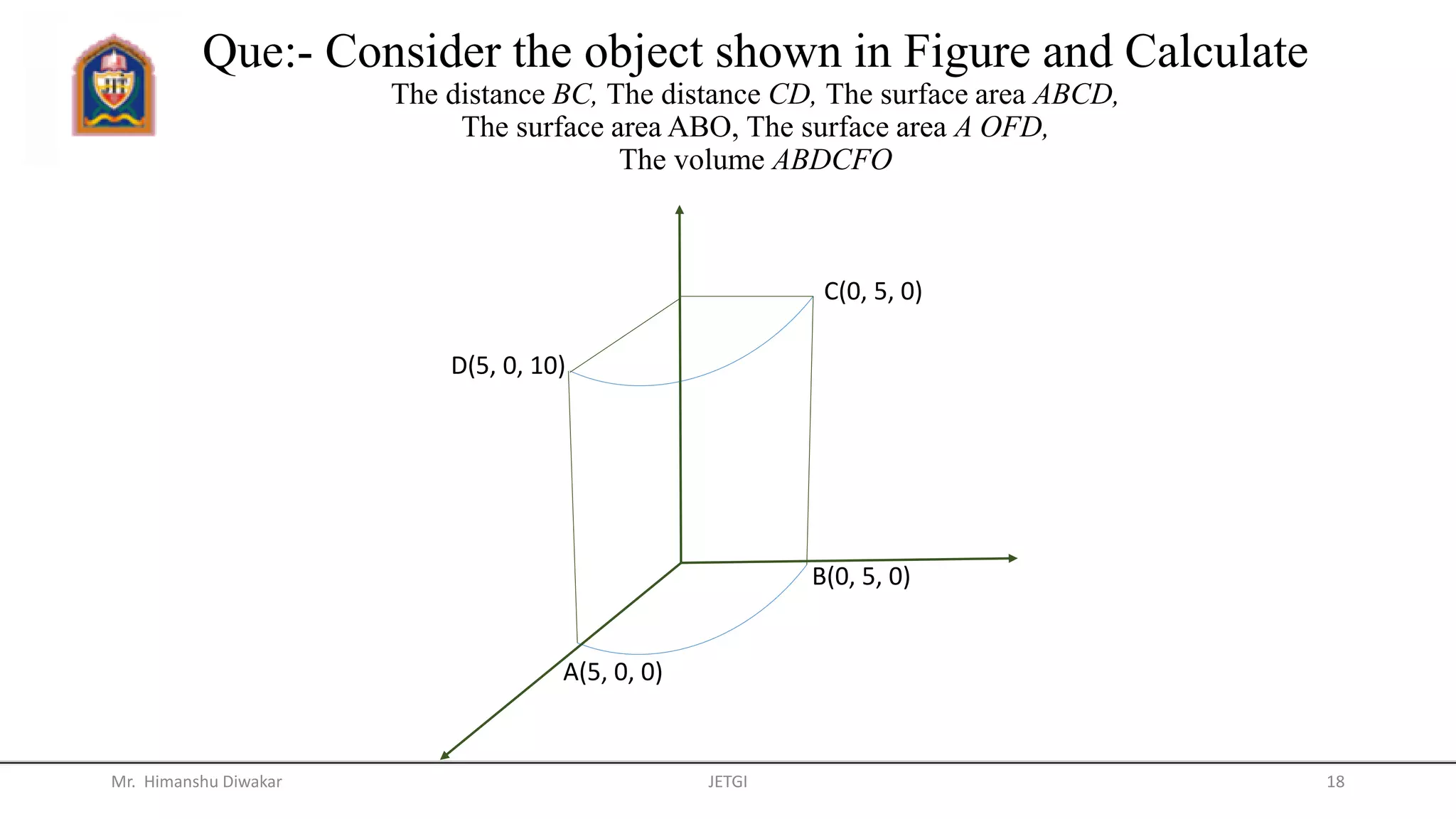
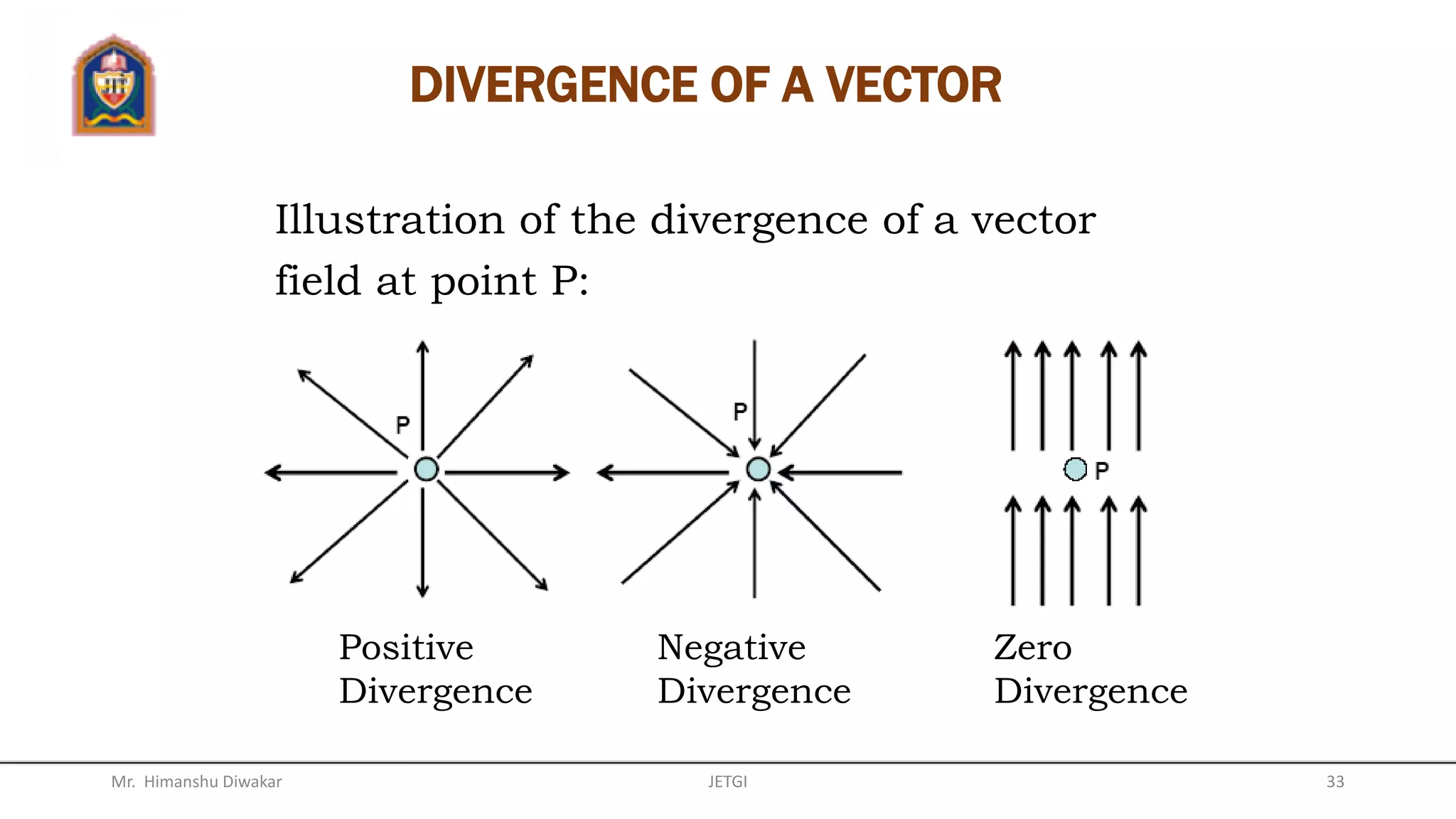
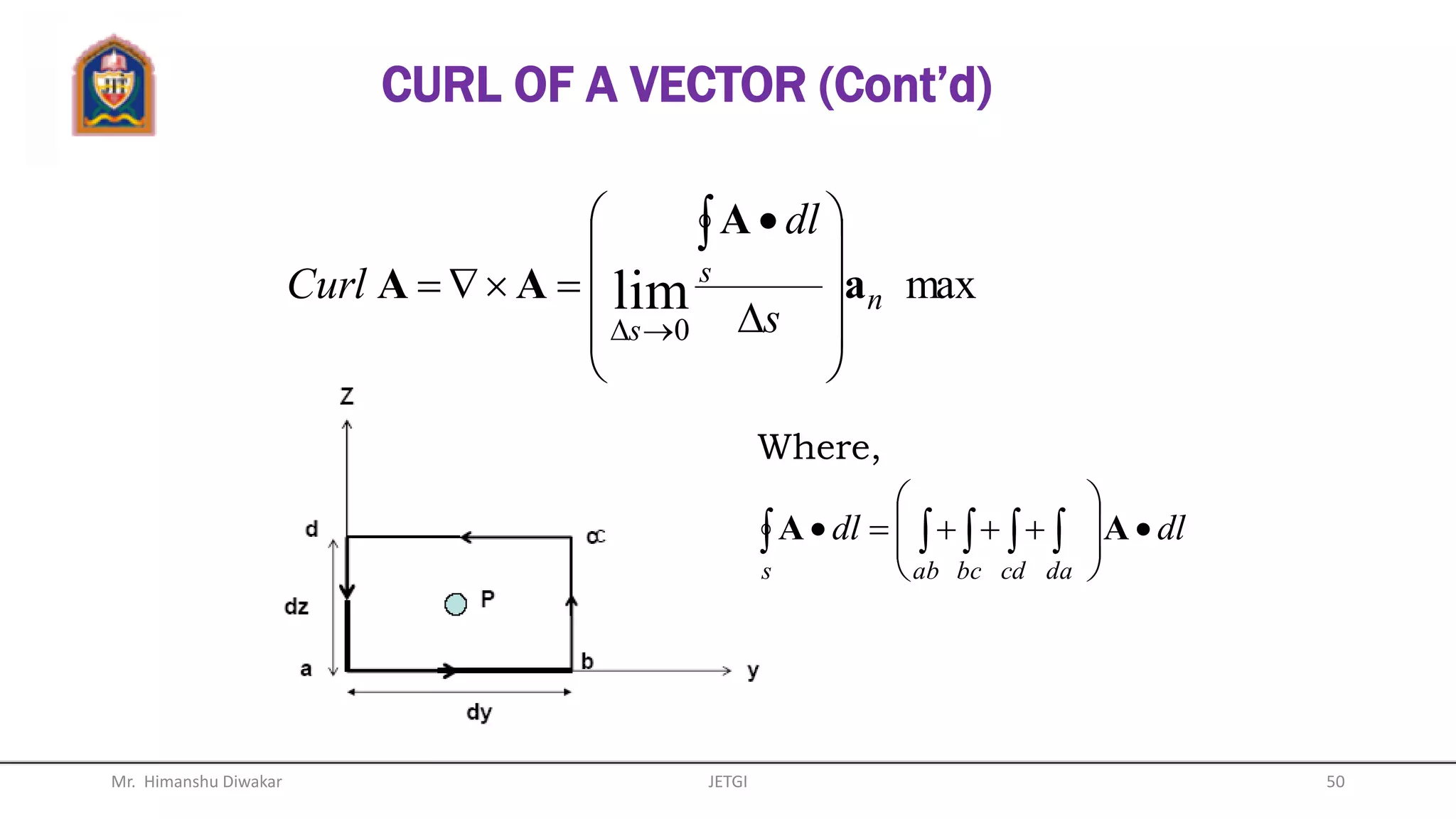
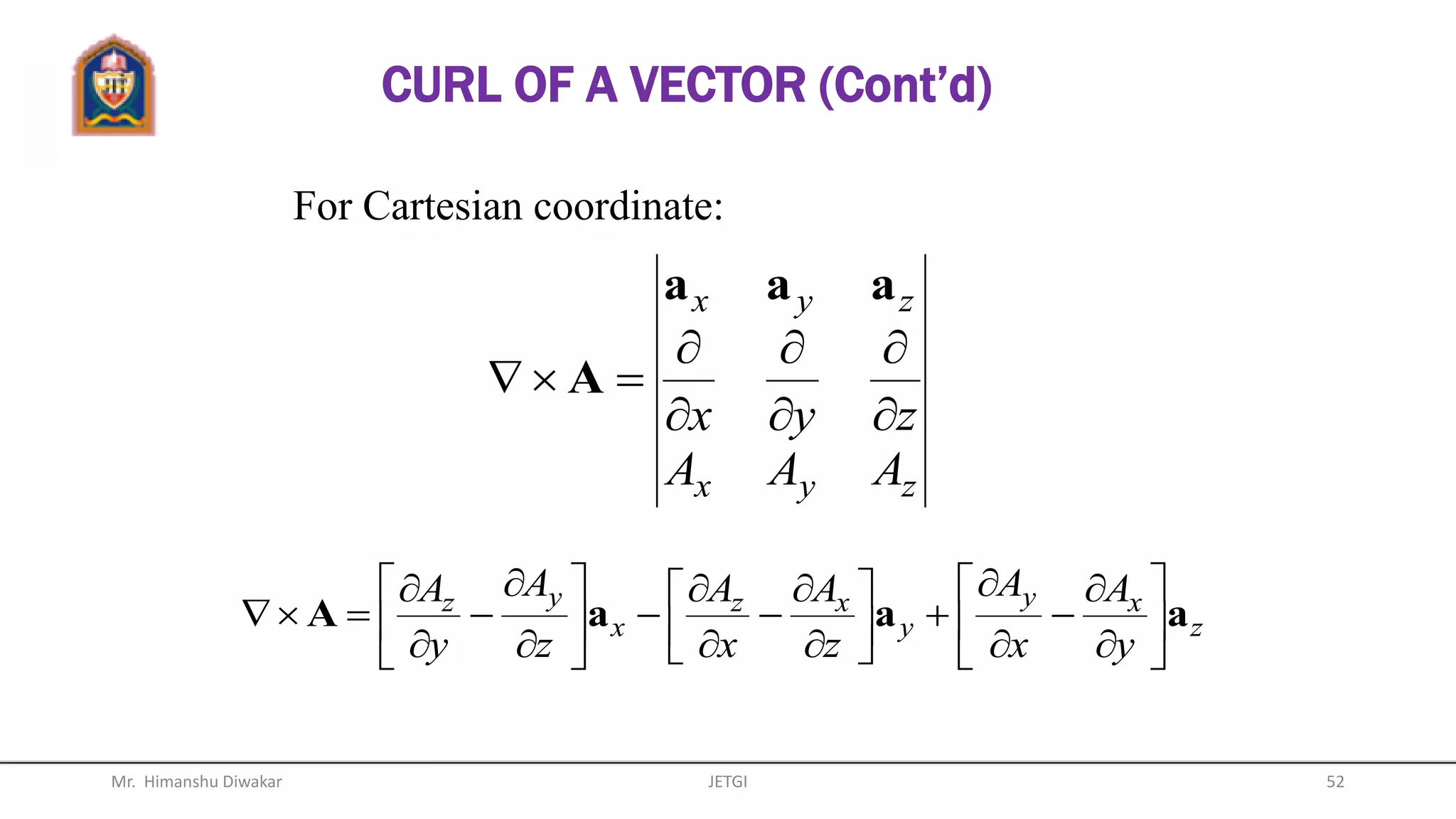
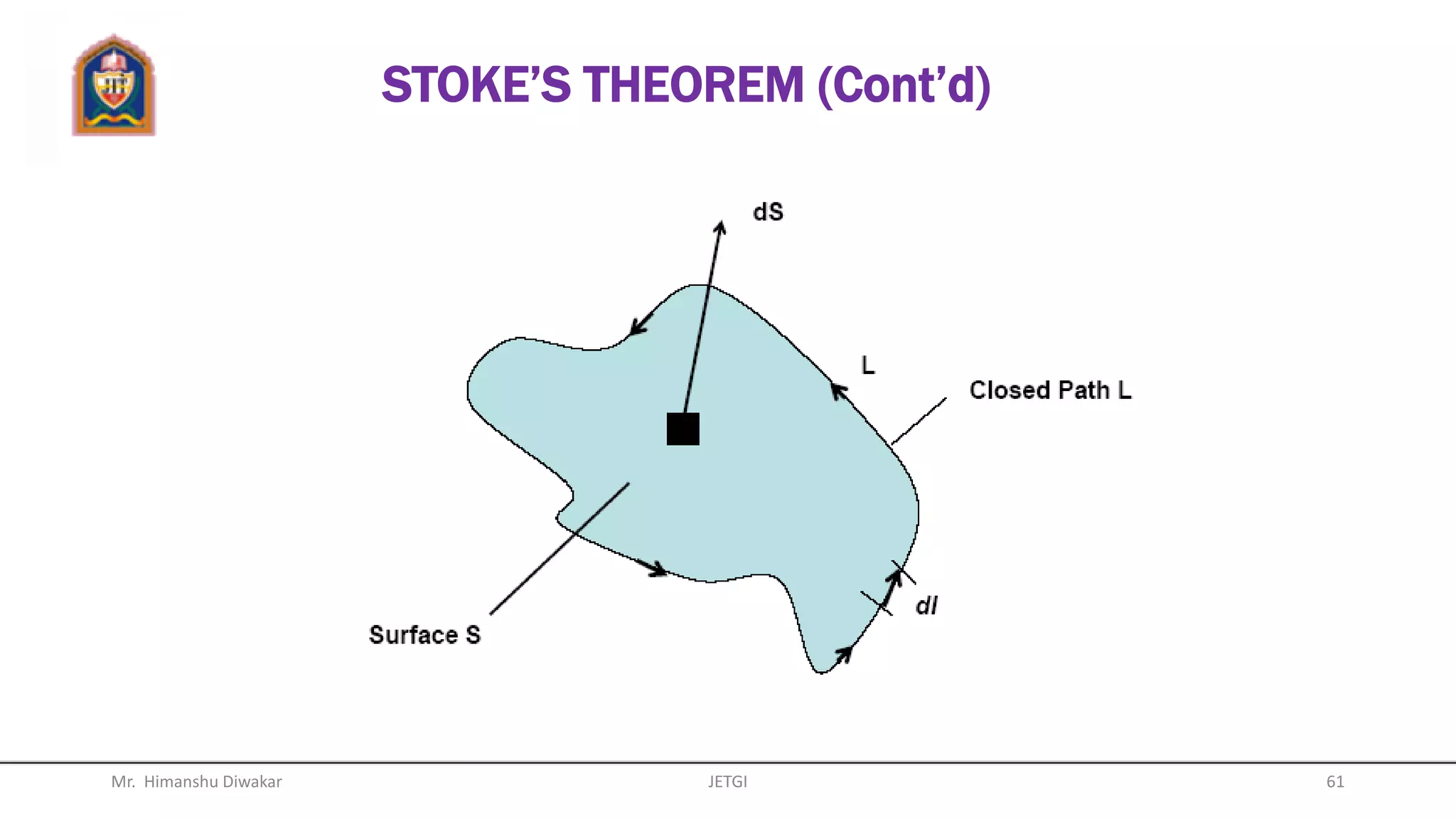
This document provides an overview of vector algebra concepts including scalars, vectors, unit vectors, position vectors, vector operations, gradients of scalars, divergence of vectors, and del operators. It defines these concepts, provides examples of their use in Cartesian, cylindrical and spherical coordinate systems, and works through examples of calculating gradients and divergences. The key topics covered are the definitions and calculations of gradients, divergences, and how to apply these concepts to vector fields in different coordinate systems.

1. Vector Algebra
Mr. HIMANSHU DIWAKAR
Assistant professor
ECED
Mr. Himanshu Diwakar 1JETGI

2. Mr. Himanshu Diwakar JETGI 2

3. VECTOR CALCULUS
Introduction
Scalars And Vectors
Gradient Of A Scalar
Divergence Of A Vector
Divergence Theorem
Curl Of A Vector
Stokes’s Theorem
Laplacian Of A Scalar
Mr. Himanshu Diwakar 3JETGI

4. Introduction
• Electromagnetics(EM):-
Interaction between electric charges
at rest
and
in motion.
• It entails the analysis, synthesis, physical interpretation, and
application of electric and magnetic fields.
Mr. Himanshu Diwakar 4JETGI

5. Scalars and vectors
• A scalar is a quantity that has only magnitude
Ex:- time, mass, distance, temperature, entropy etc.
• A vector is a quantity that has both magnitude and direction
• Velocity, force, displacement and electric field intensity.
Mr. Himanshu Diwakar JETGI 5

6. Unit vectors
Mr. Himanshu Diwakar JETGI 6
x
z
y
az
ay
ax
Unit vectors
az ,ay ,az
Similarly a A vector in Cartesian co-
ordinate
A=Ax.ax+Ay.ay+Az.az
So Unit vector of A
𝐴 =
𝐴
𝐴

7. Position and distance vector
Mr. Himanshu Diwakar JETGI 7
x
z
y
az
ay
ax
P (3, 4, 5)
O (0, 0, 0)
The distance vector is the displacement
from one point to another.
A= 3.ax+ 4.ay+ 5.az
OP distance
OP=(3−0).ax+ (4−0).ay+ (5−0).az
𝑂𝑃 = (3−0).ax+ (4−0).ay+ (5−0).az
= 9 + 16 + 25
=7.071

8. Vector multiplication
• Scalar (or dot) product = A.B
• Vector (or cross) product = A×B
• Scalar triple product : A. (B × C)
• Vector triple product :
A × B × C = B A. C − C(A. B)
Mr. Himanshu Diwakar JETGI 8

9. Angels
Mr. Himanshu Diwakar JETGI 9
If A and B are vectors then the angle between these vectors can be find
cos ∅ =
A × B
𝐴 𝐵
sin ∅ =
A. B
𝐴 𝐵

10. Differential Length (Cartesian Coordinates )
• Differential elements in length, area, and volume are useful in vector calculus.
They are defined in the Cartesian, cylindrical, and spherical coordinate systems.
1. Differential displacement is given by
2. Differential normal area is given by
3. Differential volume is given by
Mr. Himanshu Diwakar JETGI 10

11. Mr. Himanshu Diwakar JETGI 11

12. Cylindrical Coordinates
• Notice from Figure that in cylindrical coordinates, differential
elements can be found as follows:
1. Differential displacement is given by
2. Differential normal area is given by
3. Differential volume is given by
Mr. Himanshu Diwakar JETGI 12

13. Mr. Himanshu Diwakar JETGI 13

14. Mr. Himanshu Diwakar JETGI 14

15. Spherical Coordinates
From Figure, we notice that in spherical coordinates,
1. The differential displacement is
Mr. Himanshu Diwakar JETGI 15

16. 2. The differential normal area is
Mr. Himanshu Diwakar JETGI 16

17. 3. The differential volume is
Mr. Himanshu Diwakar JETGI 17

18. Que:- Consider the object shown in Figure and Calculate
The distance BC, The distance CD, The surface area ABCD,
The surface area ABO, The surface area A OFD,
The volume ABDCFO
Mr. Himanshu Diwakar JETGI 18
C(0, 5, 0)
B(0, 5, 0)
D(5, 0, 10)
A(5, 0, 0)

19. Line, Surface And Volume Integrals
• The familiar concept of integration will now be extended to cases
when the integrand involves a vector. By a line we mean the path
along a curve in space. We shall use terms such as line, curve, and
contour interchangeably.
• The line integral 𝑨. 𝒅𝒍 is the integral of the tangential component
of A along curve L.
Or simply
And For closed surface
Mr. Himanshu Diwakar JETGI 19

20. Example:-
Given that F = 𝑥2 𝑎 𝑥 − 𝑥𝑧𝑎 𝑦 − 𝑦2 𝑎 𝑧, calculate the circulation of F
around the (closed) path shown in Figure
Ans:−
1
6
Mr. Himanshu Diwakar JETGI 20

21. Dell operator
• The del operator, written 𝛻, is the vector differential operator. In
Cartesian coordinates,
• This vector differential operator, otherwise known as the gradient
operator, is not a vector in itself, but when it operates on a scalar
function, for example, a vector ensues. The operator is useful in
defining
Mr. Himanshu Diwakar JETGI 21

22. 1. The gradient of a scalar V, written, as (𝛻𝑉)
2. The divergence of a vector A, written as (𝛻 • A)
3. The curl of a vector A, written as (𝛻 X A)
4. The Laplacian of a scalar V, written as (𝛻2 𝑉)
Each of these will be denned in detail in the subsequent sections.
Mr. Himanshu Diwakar JETGI 22

23. Mr. Himanshu Diwakar JETGI 23

24. Mr. Himanshu Diwakar JETGI 24
So the solution for above equations is

25. CLASSIFICATION OF VECTOR FIELDS
• A vector field is uniquely characterized by its divergence and curl.
Neither the divergence nor curl of a vector field is sufficient to
completely describe the field.
• All vector fields can be classified in terms of their vanishing or non
vanishing divergence or curl as follows:
Mr. Himanshu Diwakar JETGI 25

26. Typical fields with vanishing and non vanishing divergence or curl.
Mr. Himanshu Diwakar JETGI 26

27. • A vector field A is said to be solenoidal (or divergenceless) if
𝛻•𝐴 = 0.
• A vector field A is said to be irrotational (or potential) if
𝛻 × 𝐴 = 0.
Mr. Himanshu Diwakar JETGI 27

28. The differential distances are the
components of the differential distance
vector :
dzdydx ,,
zyx dzdydxd aaaL 
Ld
However, from differential calculus, the differential
temperature:
dz
z
T
dy
y
T
dx
x
T
TTdT








 12
GRADIENT OF A SCALAR
Mr. Himanshu Diwakar 28JETGI

29. But,
z
y
x
ddz
ddy
ddx
aL
aL
aL



So, previous equation can be rewritten as:
Laaa
LaLaLa
d
z
T
y
T
x
T
d
z
T
d
y
T
d
x
T
dT
zyx
zyx

























GRADIENT OF A SCALAR (Cont’d)
Mr. Himanshu Diwakar 29JETGI

30. The vector inside square brackets defines the
change of temperature corresponding to a
vector change in position .
This vector is called Gradient of Scalar T.
Ld
dT
GRADIENT OF A SCALAR (Cont’d)
For Cartesian coordinate:
zyx
z
V
y
V
x
V
V aaa









Mr. Himanshu Diwakar 30JETGI

31. GRADIENT OF A SCALAR (Cont’d)
For Circular cylindrical coordinate:
z
z
VVV
V aaa








 

1
For Spherical coordinate:


aaa









V
r
V
rr
V
V r
sin
11
Mr. Himanshu Diwakar 31JETGI

32. EXAMPLE 1
Find gradient of these scalars:
yxeV z
cosh2sin

 2cos2
zU 
 cossin10 2
rW 
(a)
(b)
(c)
Mr. Himanshu Diwakar 32JETGI

33. SOLUTION TO EXAMPLE 1
(a) Use gradient for Cartesian coordinate:
z
z
y
z
x
z
zyx
yxe
yxeyxe
z
V
y
V
x
V
V
a
aa
aaa
cosh2sin
sinh2sincosh2cos2













Mr. Himanshu Diwakar 33JETGI

34. SOLUTION TO EXAMPLE 1 (Cont’d)
(b) Use gradient for Circular cylindrical
coordinate:
z
z
zz
z
UUU
U
a
aa
aaa





2cos
2sin22cos2
1
2











Mr. Himanshu Diwakar 34JETGI

35. SOLUTION TO EXAMPLE 1 (Cont’d)
(c) Use gradient for Spherical coordinate:






a
aa
aaa
sinsin10
cos2sin10cossin10
sin
11
2











r
r
W
r
W
rr
W
W
Mr. Himanshu Diwakar 35JETGI

36. DIVERGENCE OF A VECTOR
Illustration of the divergence of a vector
field at point P:
Positive
Divergence
Negative
Divergence
Zero
Divergence
Mr. Himanshu Diwakar 36JETGI

37. DIVERGENCE OF A VECTOR (Cont’d)
The divergence of A at a given point P
is the outward flux per unit volume:
v
dS
div s
v 




A
AA lim
0
Mr. Himanshu Diwakar 37JETGI

38. DIVERGENCE OF A VECTOR (Cont’d)
What is ?? 
s
dSA Vector field A at
closed surface S
Mr. Himanshu Diwakar 38JETGI

39. Where,
dSdS
bottomtoprightleftbackfronts









  AA
And, v is volume enclosed by surface S
DIVERGENCE OF A VECTOR (Cont’d)
Mr. Himanshu Diwakar 39JETGI

40. For Cartesian coordinate:
z
A
y
A
x
A zyx








 A
For Circular cylindrical coordinate:
  z
AA
A z














11
A
DIVERGENCE OF A VECTOR (Cont’d)
Mr. Himanshu Diwakar 40JETGI

41. For Spherical coordinate:
   













A
r
A
r
Ar
rr
r
sin
1sin
sin
11 2
2
A
DIVERGENCE OF A VECTOR (Cont’d)
Mr. Himanshu Diwakar 41JETGI

42. EXAMPLE 11
Find divergence of these vectors:
zx xzyzxP aa  2
zzzQ aaa   cossin 2

  aaa coscossincos
1
2
 r
r
W r
(a)
(b)
(c)
Mr. Himanshu Diwakar 42JETGI

43. 43
(a) Use divergence for Cartesian
coordinate:
SOLUTION TO EXAMPLE 11
     
xxyz
xz
zy
yzx
x
z
P
y
P
x
P zyx



















2
02
P
Mr. Himanshu Diwakar JETGI

44. (b) Use divergence for Circular cylindrical
coordinate:
 
     










cossin2
cos
1
sin
1
11
22


















 Q
z
z
z
z
QQ
Q z
SOLUTION TO EXAMPLE 11 (Cont’d)
Mr. Himanshu Diwakar 44JETGI

45. SOLUTION TO EXAMPLE 11 (Cont’d)
(c) Use divergence for Spherical coordinate:
   
   
 










coscos2
cos
sin
1
cossin
sin
1
cos
1
sin
1sin
sin
11
2
2
2
2


















 W
r
r
rrr
W
r
W
r
Wr
rr
r
Mr. Himanshu Diwakar 45JETGI

46. It states that the total outward flux of a vector
field A at the closed surface S is the same as
volume integral of divergence of A.
 
VV
dVdS AA
DIVERGENCE THEOREM
Mr. Himanshu Diwakar 46JETGI

47. EXAMPLE 12
A vector field exists in the region
between two concentric cylindrical surfaces
defined by ρ = 1 and ρ = 2, with both cylinders
extending between z = 0 and z = 5. Verify the
divergence theorem by evaluating:
 aD 3


 
S
dsD
 
V
DdV
(a)
(b)
Mr. Himanshu Diwakar 47JETGI

48. SOLUTION TO EXAMPLE 12
(a) For two concentric cylinder, the left side:
topbottomouterinner
S
d DDDDSD 
Where,










10)(
)(
2
0
5
0
1
4
2
0
5
0
1
3


 
 
 

 

z
z
inner
dzd
dzdD
aa
aa
Mr. Himanshu Diwakar 48JETGI

49. 









160)(
)(
2
0
5
0
2
4
2
0
5
0
2
3


 
 
 

 

z
z
outer
dzd
dzdD
aa
aa
 
 
 

 



2
1
2
0
5
3
2
1
2
0
0
3
0)(
0)(










z
ztop
z
zbottom
ddD
ddD
aa
aa
SOLUTION TO EXAMPLE 12 Cont’d)
Mr. Himanshu Diwakar 49JETGI

50. Therefore


150
0016010

 SD
S
d
SOLUTION TO EXAMPLE 12 Cont’d)
Mr. Himanshu Diwakar 50JETGI

51. SOLUTION TO EXAMPLE 12 Cont’d)
(b) For the right side of Divergence Theorem,
evaluate divergence of D
  23
4
1





 D
So,





 
150
4
5
0
2
0
2
1
4
5
0
2
0
2
1
2





























  
  
z
r
z
dzdddVD
Mr. Himanshu Diwakar 51JETGI

52. CURL OF A VECTOR
The curl of vector A is an axial
(rotational) vector whose magnitude is
the maximum circulation of A per unit
area tends to zero and whose direction
is the normal direction of the area
when the area is oriented so as to
make the circulation maximum.
Mr. Himanshu Diwakar 52JETGI

53. maxlim
0
a
A
AA n
s
s s
dl
Curl















Where,
CURL OF A VECTOR (Cont’d)
dldl
dacdbcabs








  AA
Mr. Himanshu Diwakar 53JETGI

54. CURL OF A VECTOR (Cont’d)
The curl of the vector field is concerned with rotation of
the vector field. Rotation can be used to measure the
uniformity of the field, the more non uniform the field,
the larger value of curl.
Mr. Himanshu Diwakar 54JETGI

55. For Cartesian coordinate:
CURL OF A VECTOR (Cont’d)
zyx
zyx
AAA
zyx 






aaa
A
z
xy
y
xz
x
yz
y
A
x
A
z
A
x
A
z
A
y
A
aaaA 































Mr. Himanshu Diwakar 55JETGI

56. z
z
AAA
z





 






aaa
A
1
 
z
zz
AA
z
AA
z
AA
a
aaA












































1
1
For Circular cylindrical coordinate:
CURL OF A VECTOR (Cont’d)
Mr. Himanshu Diwakar 56JETGI

57. CURL OF A VECTOR (Cont’d)
For Spherical coordinate:
  



ArrAA
rr
r
r
sin
sin
1
2







aaa
A
   
 








a
aaA



































r
r
r
A
r
rA
r
r
rAA
r
AA
r
)(1
sin
11sin
sin
1
Mr. Himanshu Diwakar 57JETGI

58. EXAMPLE 13
zx xzyzxP aa  2
zzzQ aaa   cossin 2

  aaa coscossincos
1
2
 r
r
W r
(a)
(b)
(c)
Find curl of these vectors:
Mr. Himanshu Diwakar 58JETGI

59. SOLUTION TO EXAMPLE 13
(a) Use curl for Cartesian coordinate:
     
  zy
zyx
z
xy
y
xz
x
yz
zxzyx
zxzyx
y
P
x
P
z
P
x
P
z
P
y
P
aa
aaa
aaaP
22
22
000


































Mr. Himanshu Diwakar 59JETGI

60. (b) Use curl for Circular cylindrical coordinate
 
 
 
    z
z
z
zz
zz
z
z
y
Q
x
QQ
z
Q
z
QQ
aa
a
aa
aaaQ















cos3sin
1
cos3
1
00sin
11
3
2
2













































SOLUTION TO EXAMPLE 13 (Cont’d)
Mr. Himanshu Diwakar 60JETGI

61. (c) Use curl for Spherical coordinate:
   
 
     





















a
aa
a
aaW






















































































22
2
cos
)cossin(1
cos
cos
sin
11cossinsincos
sin
1
)(1
sin
11sin
sin
1
r
r
r
r
r
rr
r
r
r
W
r
rW
r
r
rWW
r
WW
r
r
r
r
r
SOLUTION TO EXAMPLE 13 (Cont’d)
Mr. Himanshu Diwakar 61JETGI

62. SOLUTION TO EXAMPLE 13 (Cont’d)
   
a
aa
a
aa













sin
1
cos2
cos
sin
sin
2cos
sin
cossin2
1
cos0
1
sinsin2cos
sin
1
3
2






















r
rr
r
r
r
r
r
r
r
r
Mr. Himanshu Diwakar 62JETGI

63. STOKE’S THEOREM
The circulation of a vector field A around
a closed path L is equal to the surface
integral of the curl of A over the open
surface S bounded by L that A and curl
of A are continuous on S.
  
SL
dSdl AA
Mr. Himanshu Diwakar 63JETGI

64. STOKE’S THEOREM (Cont’d)
Mr. Himanshu Diwakar 64JETGI

65. EXAMPLE 14
By using Stoke’s Theorem, evaluate
for
  dlA
  aaA sincos 

Mr. Himanshu Diwakar 65JETGI

66. EXAMPLE 14 (Cont’d)
Mr. Himanshu Diwakar 66JETGI

67. SOLUTION TO EXAMPLE 14
Stoke’s Theorem,
  
SL
dSdl AA
where, andzddd aS 
Evaluate right side to get left side,
  zaA 

sin1
1

Mr. Himanshu Diwakar 67JETGI

68. SOLUTION TO EXAMPLE 14 (Cont’d)
   
941.4
sin1
1
0
0
60
30
5
2

  
 
aA z
S
dddS 
 
Mr. Himanshu Diwakar 68JETGI

69. EXAMPLE 15
Verify Stoke’s theorem for the vector field
for given figure by evaluating:  aaB sincos 

(a) over the
semicircular contour.
  LB d
(b) over the
surface of semicircular
contour.
   SB d
Mr. Himanshu Diwakar 69JETGI

70. SOLUTION TO EXAMPLE 15
(a) To find  LB d
 
321 LLL
dddd LBLBLBLB
Where,
   

 
dd
dzddd z
sincos
sincos

 aaaaaLB
Mr. Himanshu Diwakar 70JETGI

71. So
20
2
1
sincos
2
0
2
0
0
0
0,0
2
01


































LB
zz
L
ddd
  4cos20
sincos
0
0,2
0
0
2
22































LB
zz
L
ddd
SOLUTION TO EXAMPLE 15 (Cont’d)
Mr. Himanshu Diwakar 71JETGI

72. 20
2
1
sincos
0
2
2
00,0
0
23































r
zz
L
ddd




LB
SOLUTION TO EXAMPLE 15 (Cont’d)
Therefore the closed integral,
8242  LB d
Mr. Himanshu Diwakar 72JETGI

73. SOLUTION TO EXAMPLE 15 (Cont’d)
(b) To find    SB d
 
       
   
     
z
z
z
zz
a
aaa
a
aa
aaB



























































1
1sin
sinsin
1
00
cossin
1
0cossin0
1
sincos
Mr. Himanshu Diwakar 73JETGI

74. SOLUTION TO EXAMPLE 15 (Cont’d)
Therefore
 
8
2
1
cos
1sin
1
1sin
0
2
0
2
0
2
0
0
2
0






































 
 
 
 




 

 




 aaSB
dd
ddd zz
Mr. Himanshu Diwakar 74JETGI

75. LAPLACIAN OF A SCALAR
The Laplacian of a scalar field, V
written as:
V2

Where, Laplacian V is:






























zyxzyx
z
V
y
V
x
V
zyx
VV
aaaaaa
2
Mr. Himanshu Diwakar 75JETGI

76. For Cartesian coordinate:
2
2
2
2
2
2
2
z
V
y
V
x
V
V









For Circular cylindrical coordinate:
2
22
2
2 11
z
VVV
V



















LAPLACIAN OF A SCALAR (Cont’d)
Mr. Himanshu Diwakar 76JETGI

77. LAPLACIAN OF A SCALAR (Cont’d)
For Spherical coordinate:
2
2
22
2
2
2
2
sin
1
sin
sin
11




























V
r
V
rr
V
r
rr
V
Mr. Himanshu Diwakar 77JETGI

78. EXAMPLE 16
Find Laplacian of these scalars:
yxeV z
cosh2sin

 2cos2
zU 
 cossin10 2
rW 
(a)
(b)
(c)
Try yourself !!
Mr. Himanshu Diwakar 78JETGI

79. SOLUTION TO EXAMPLE 16
yxeV z
cosh2sin22 

02
 U
 

2cos21
cos102

r
W
(a)
(b)
(c)
Mr. Himanshu Diwakar 79JETGI

80. THANK YOU
Mr. Himanshu Diwakar 80JETGI