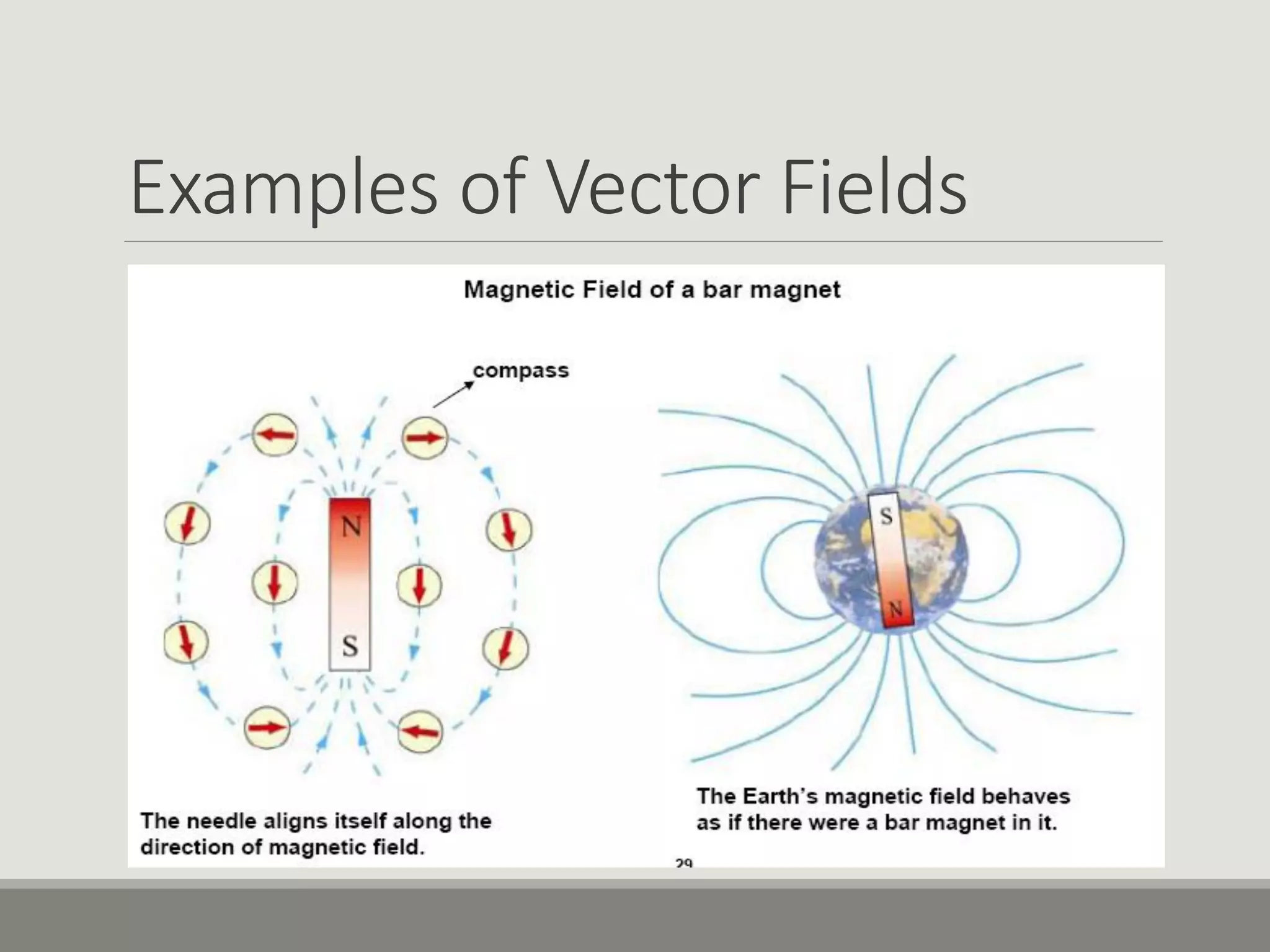
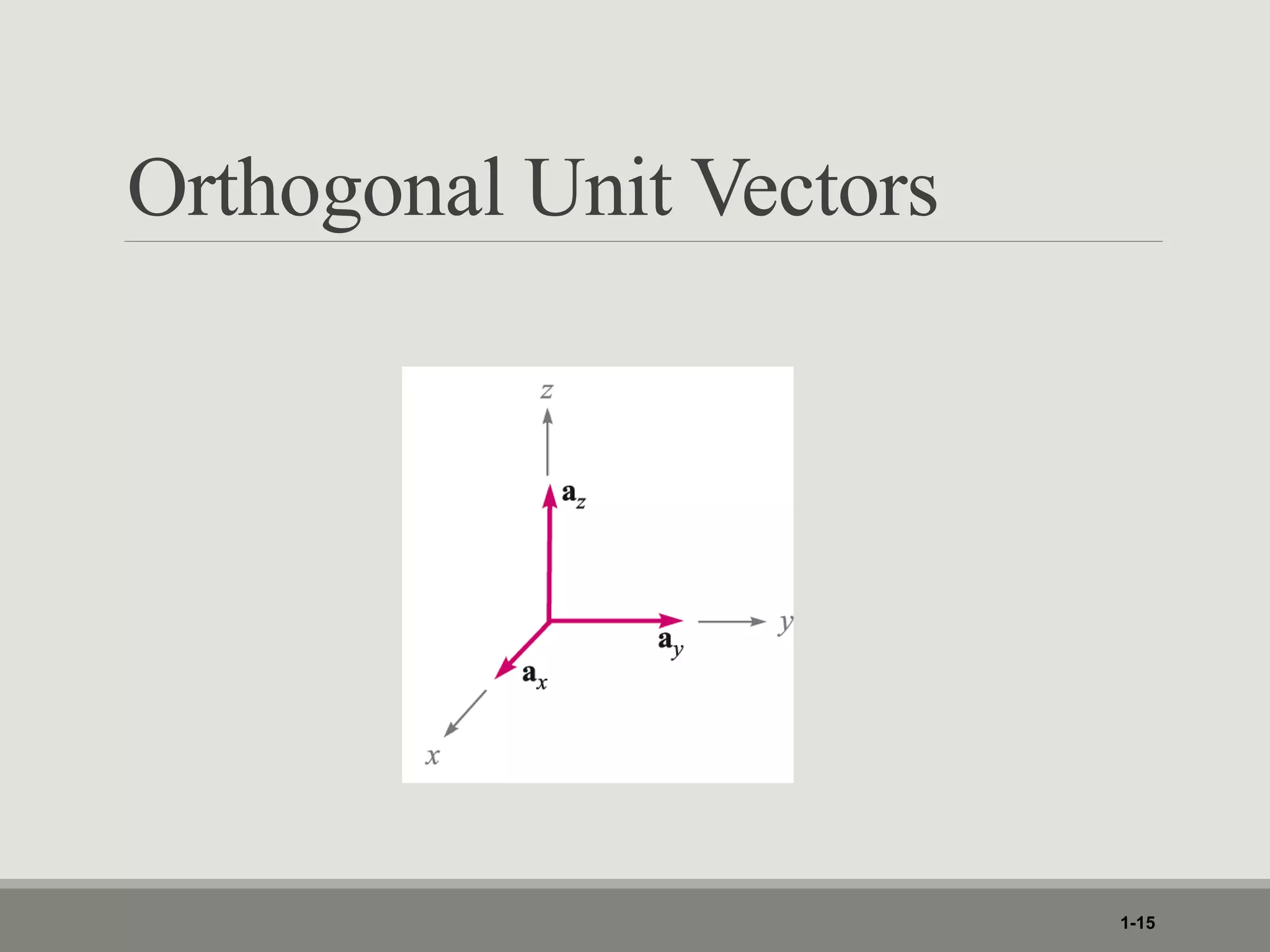
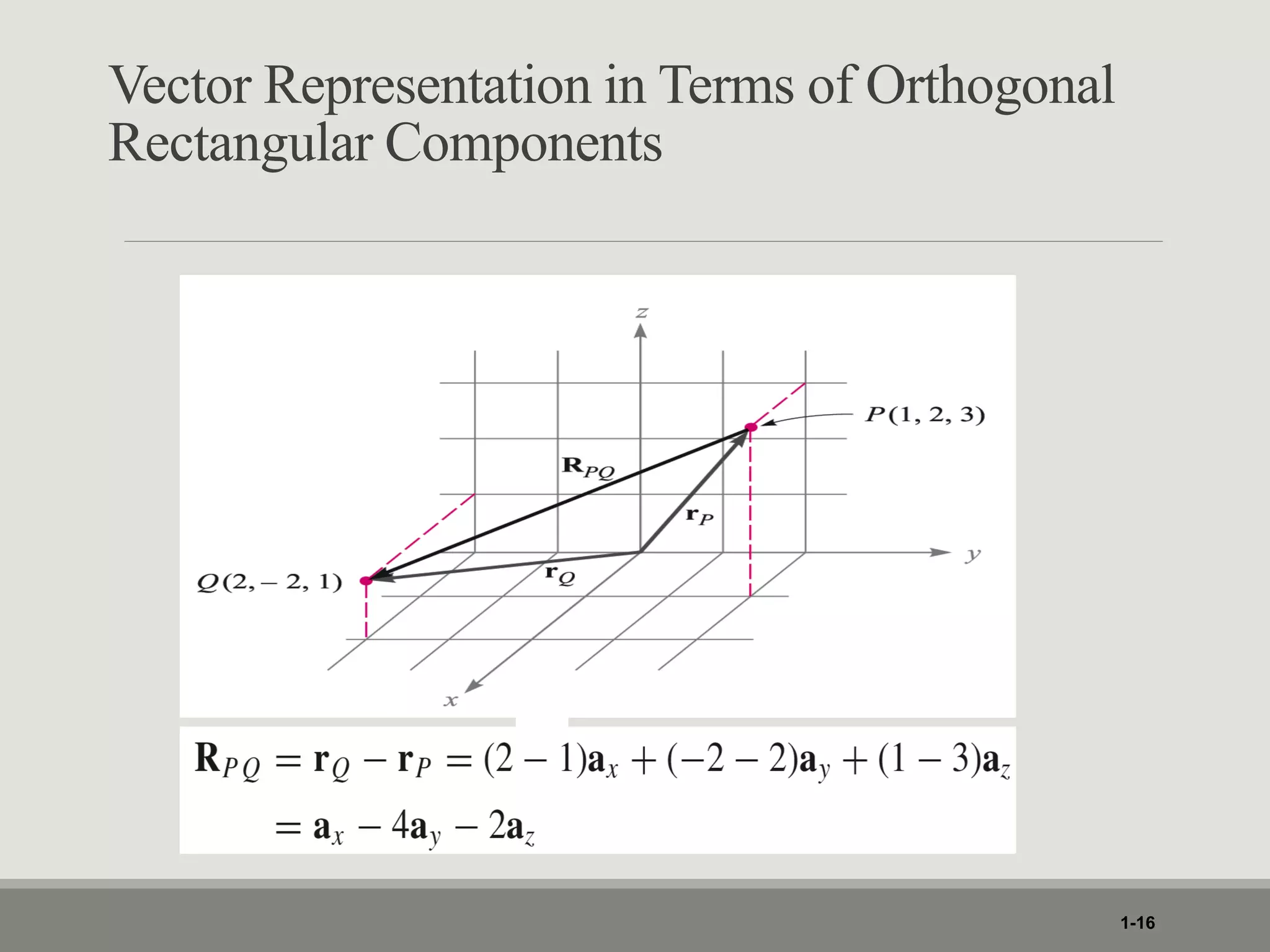
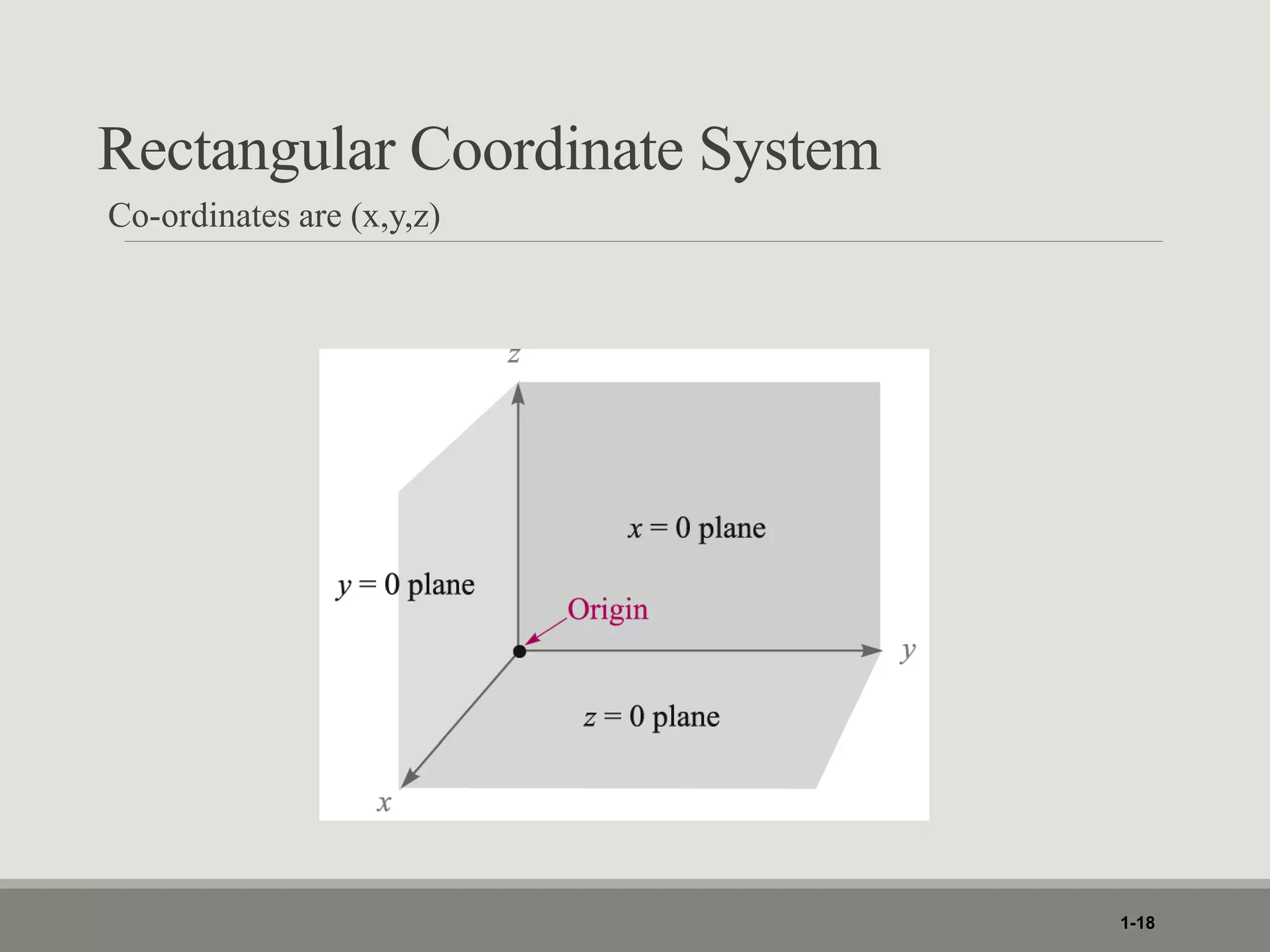
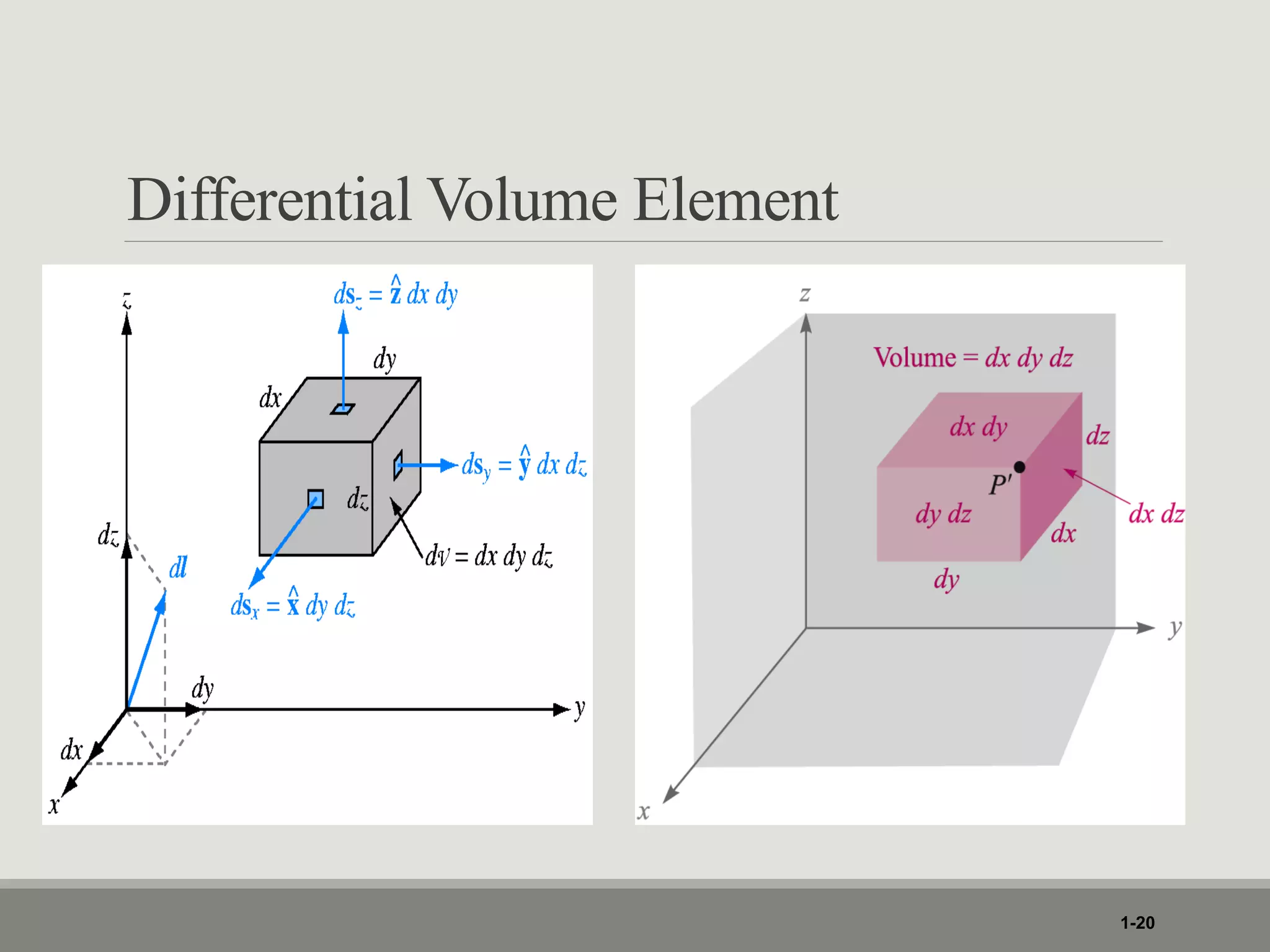
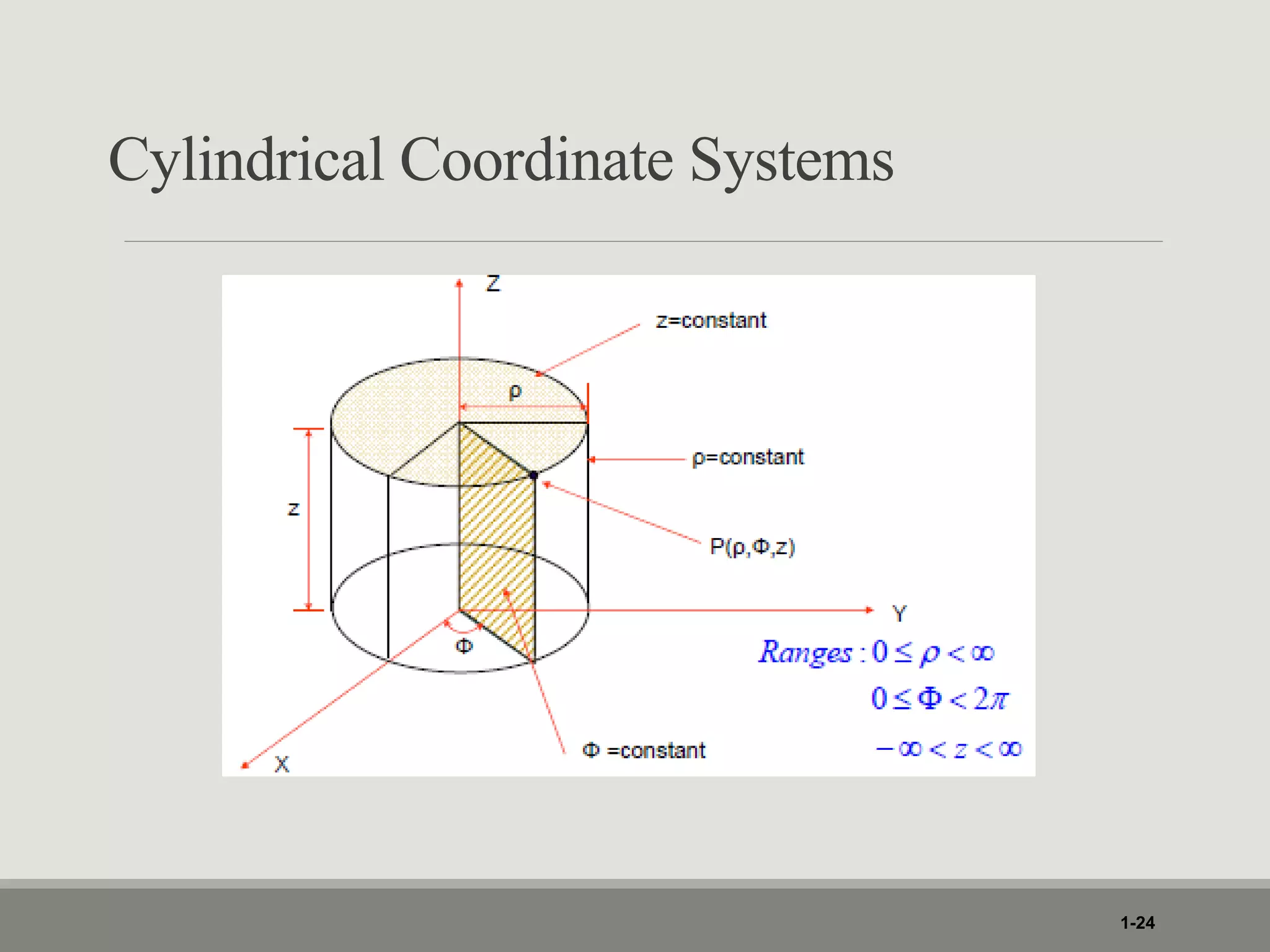
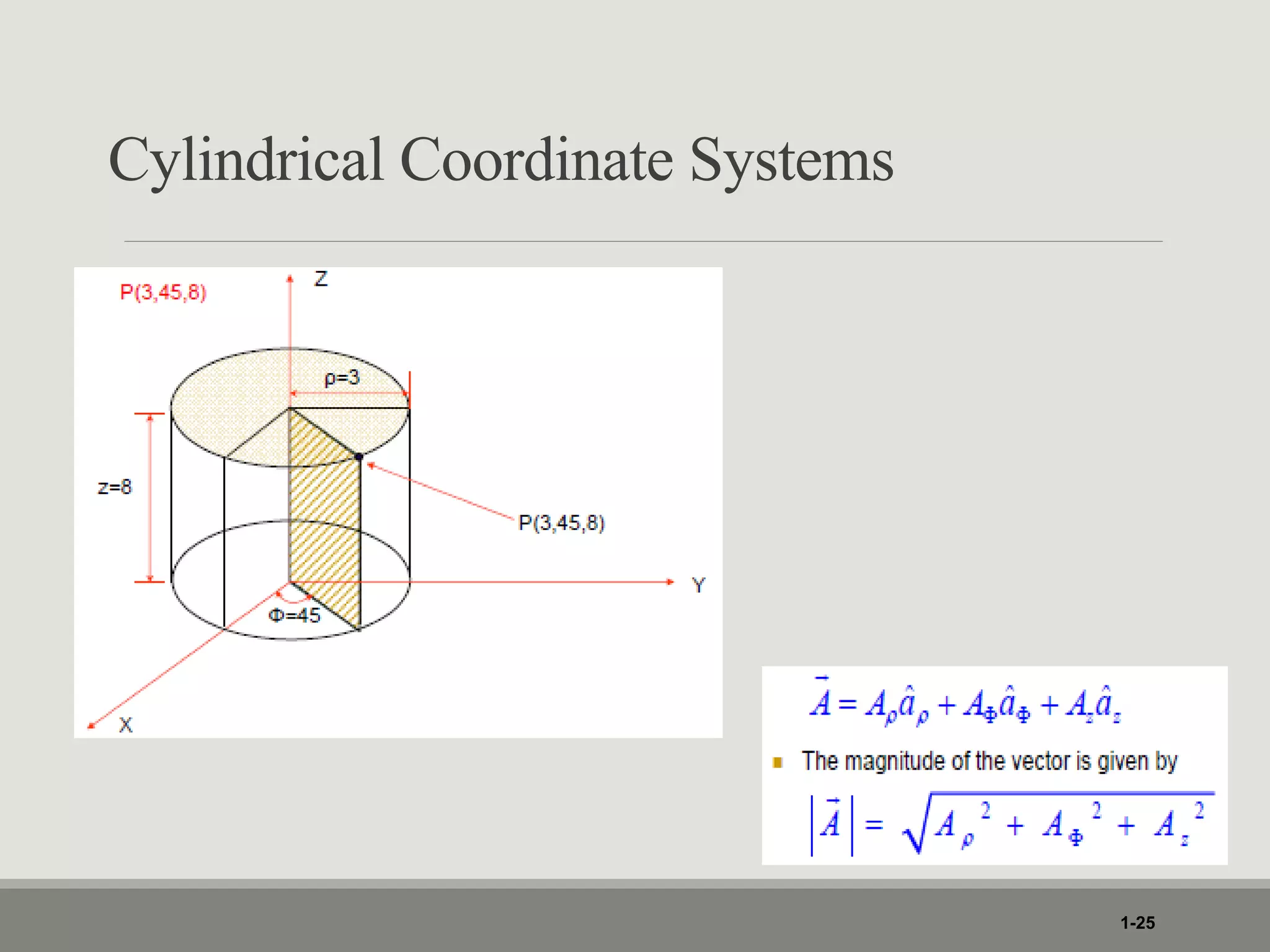
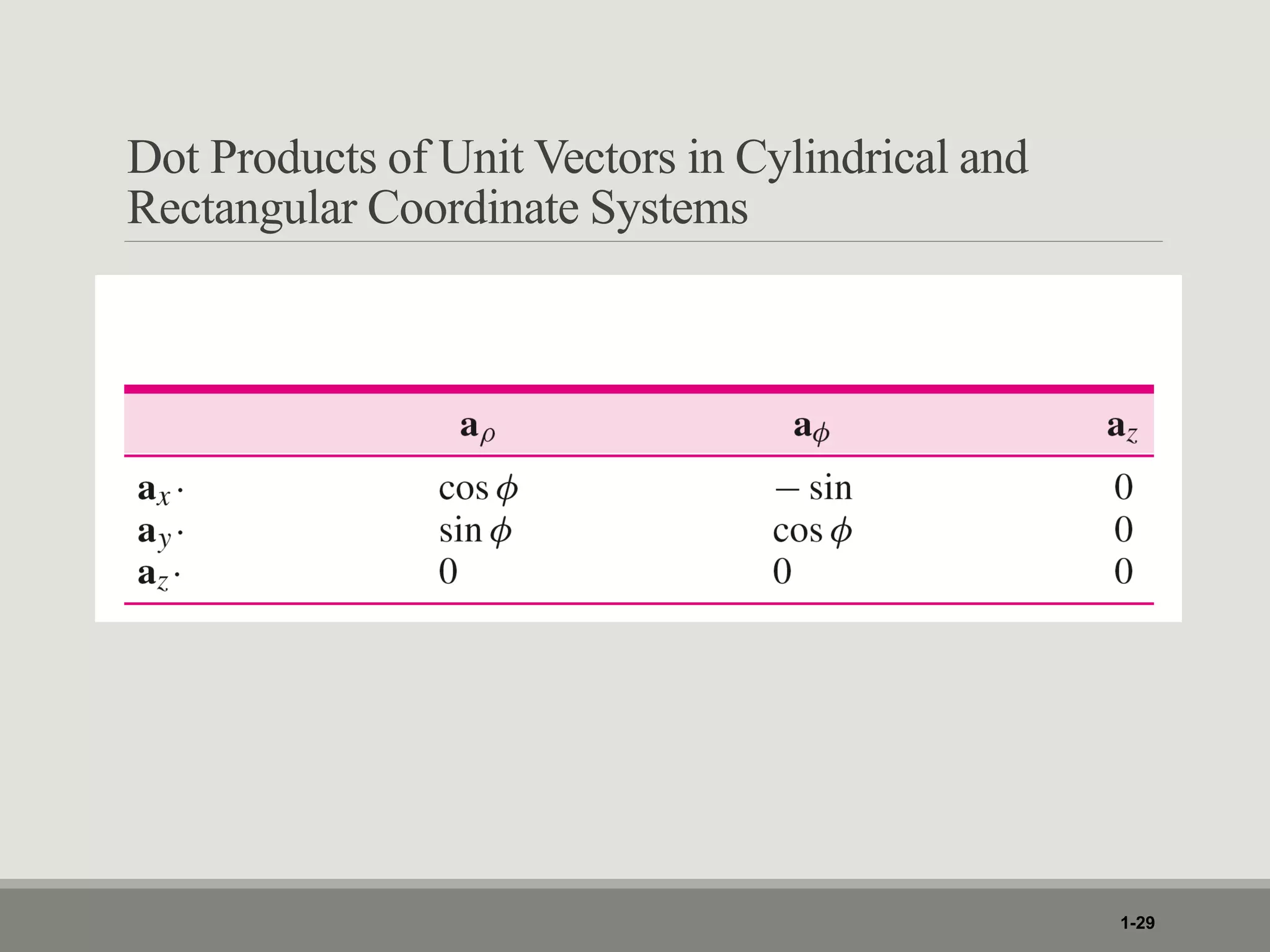
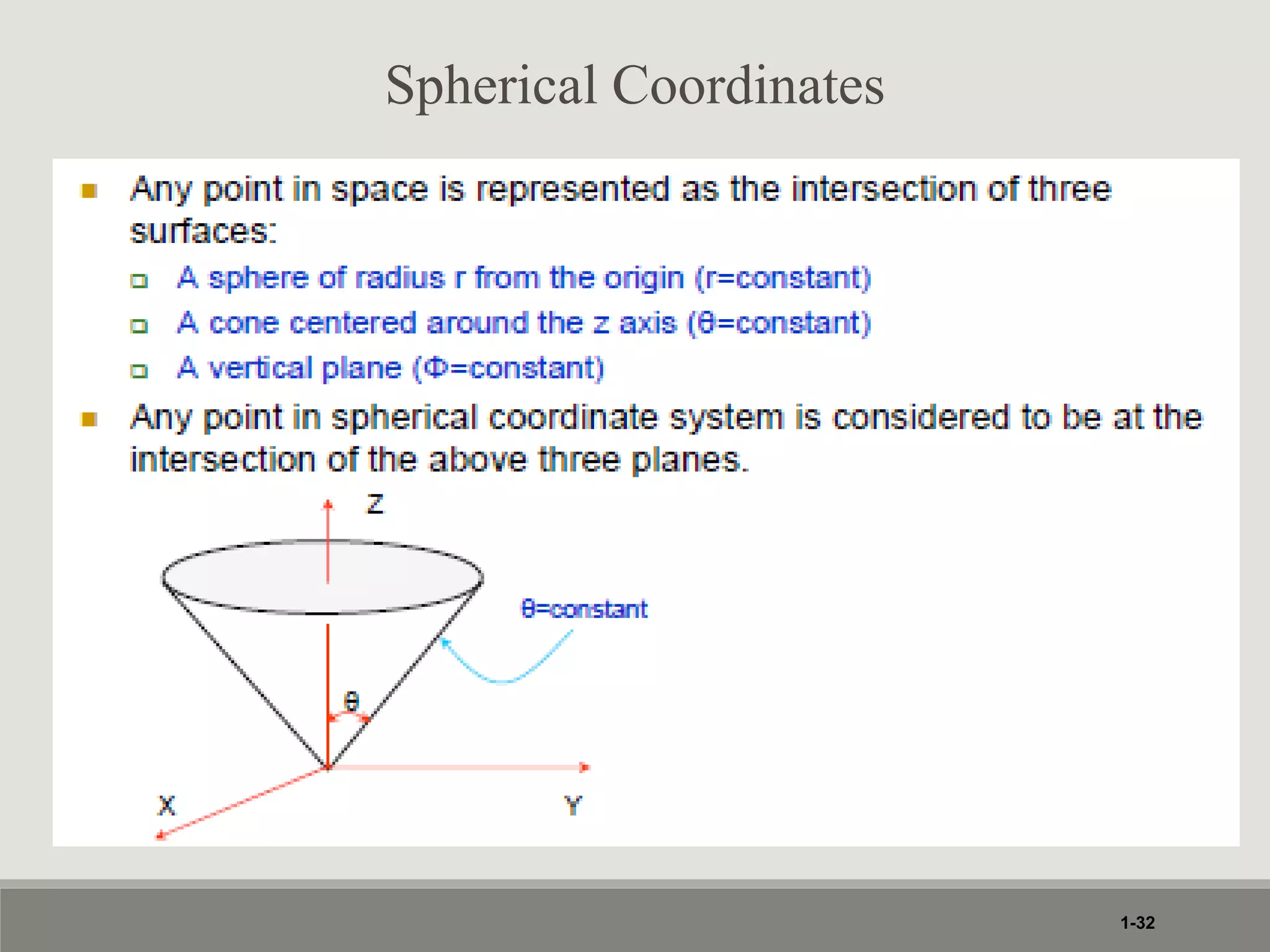
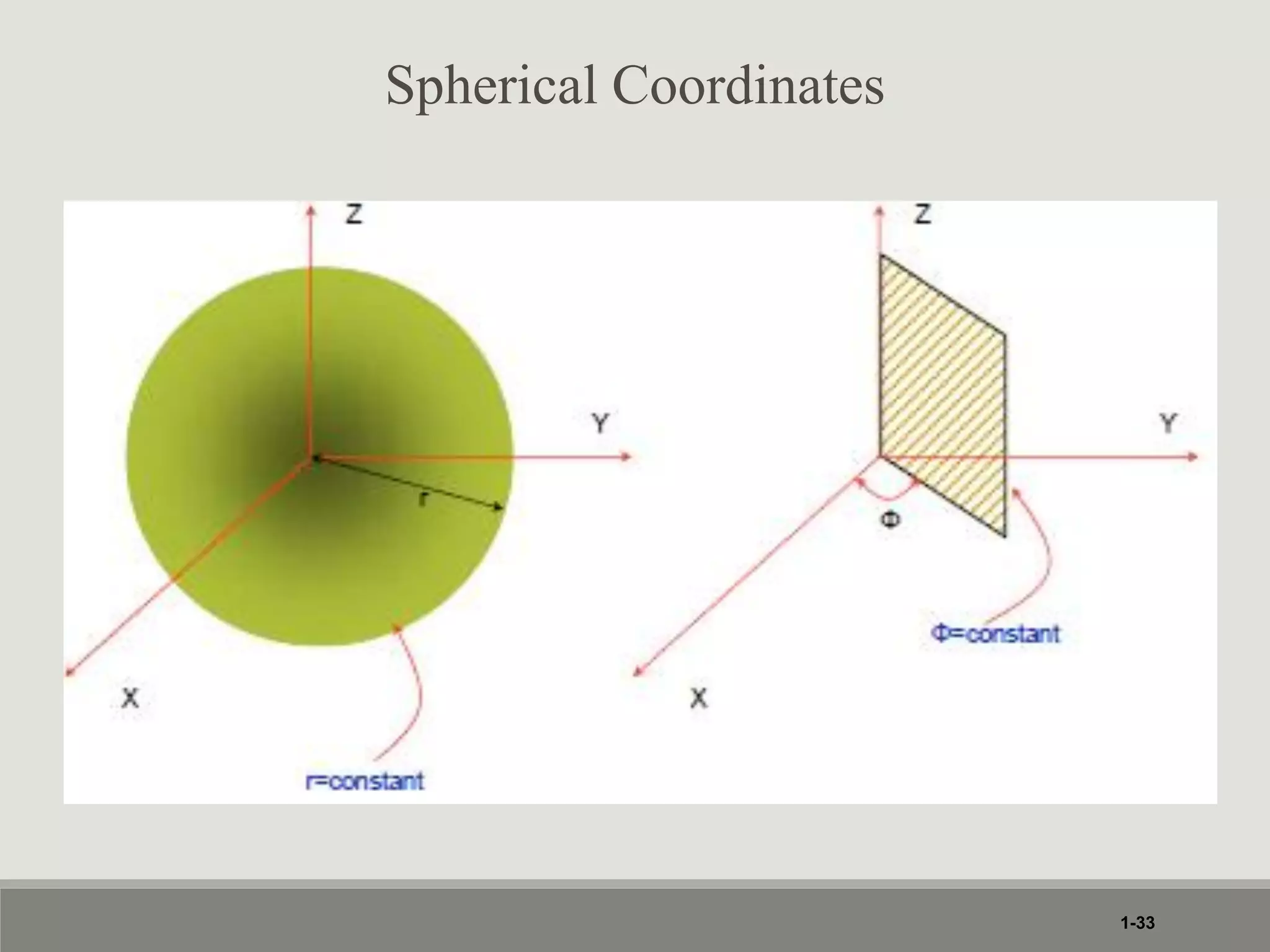
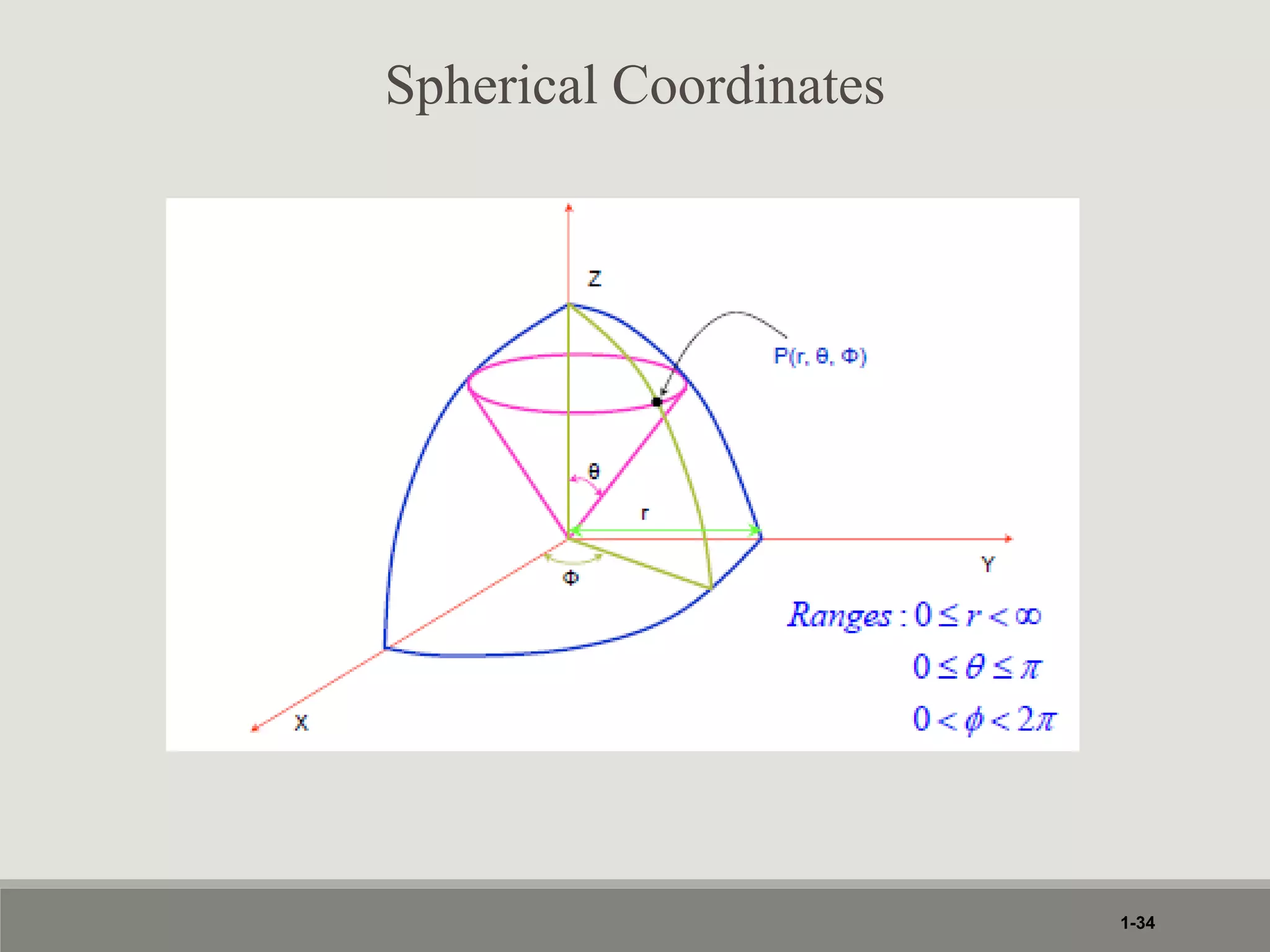
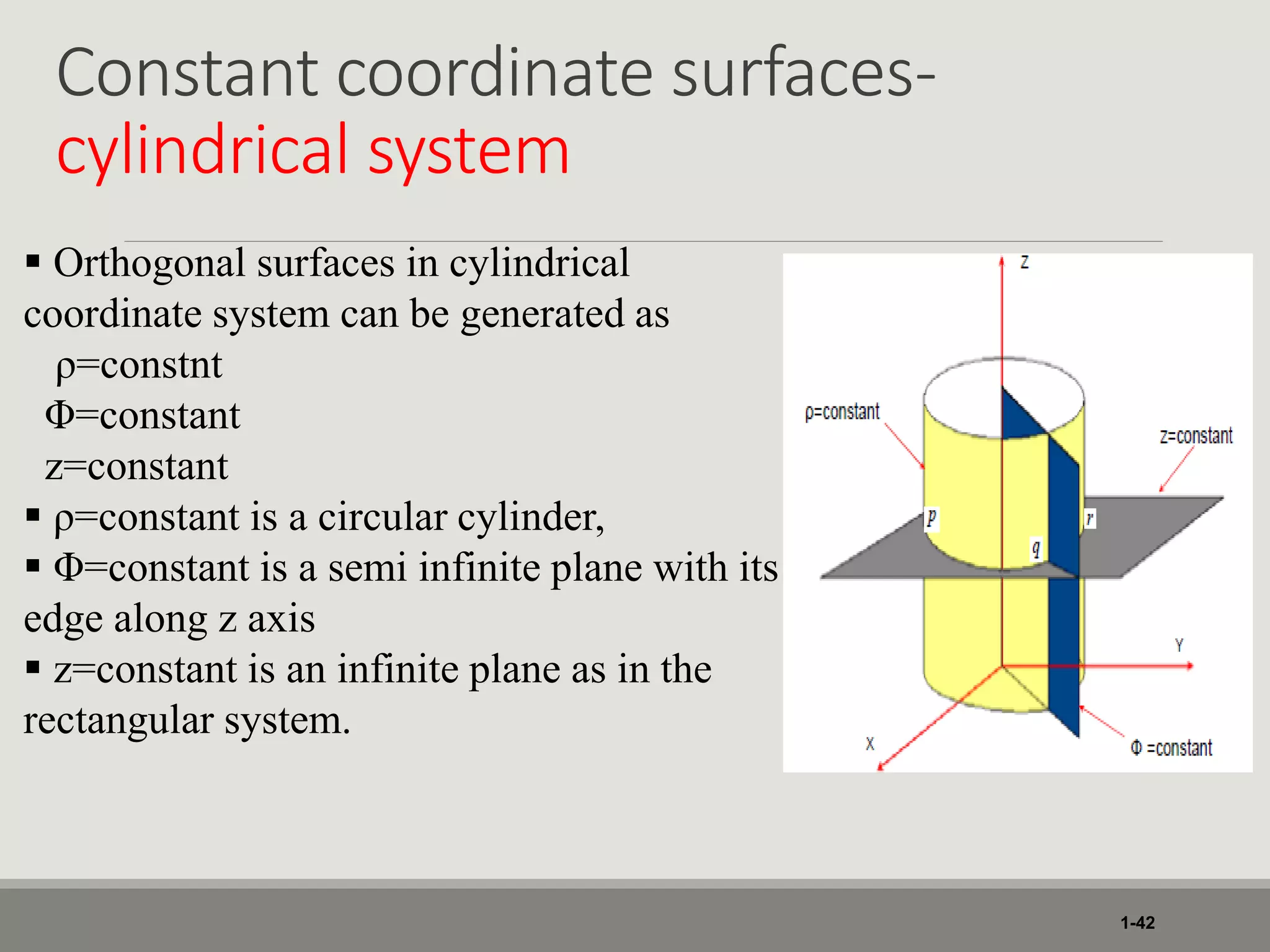
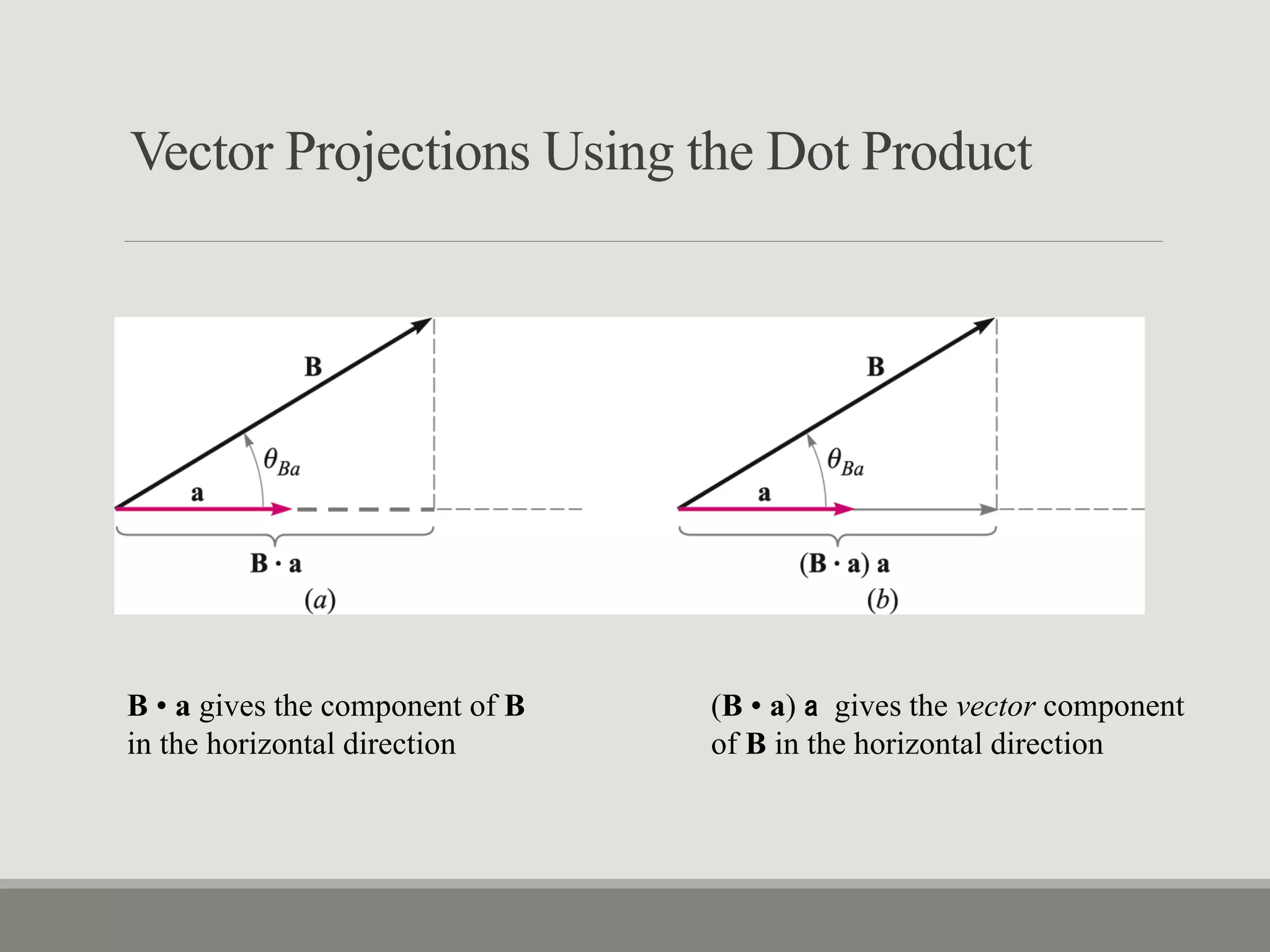
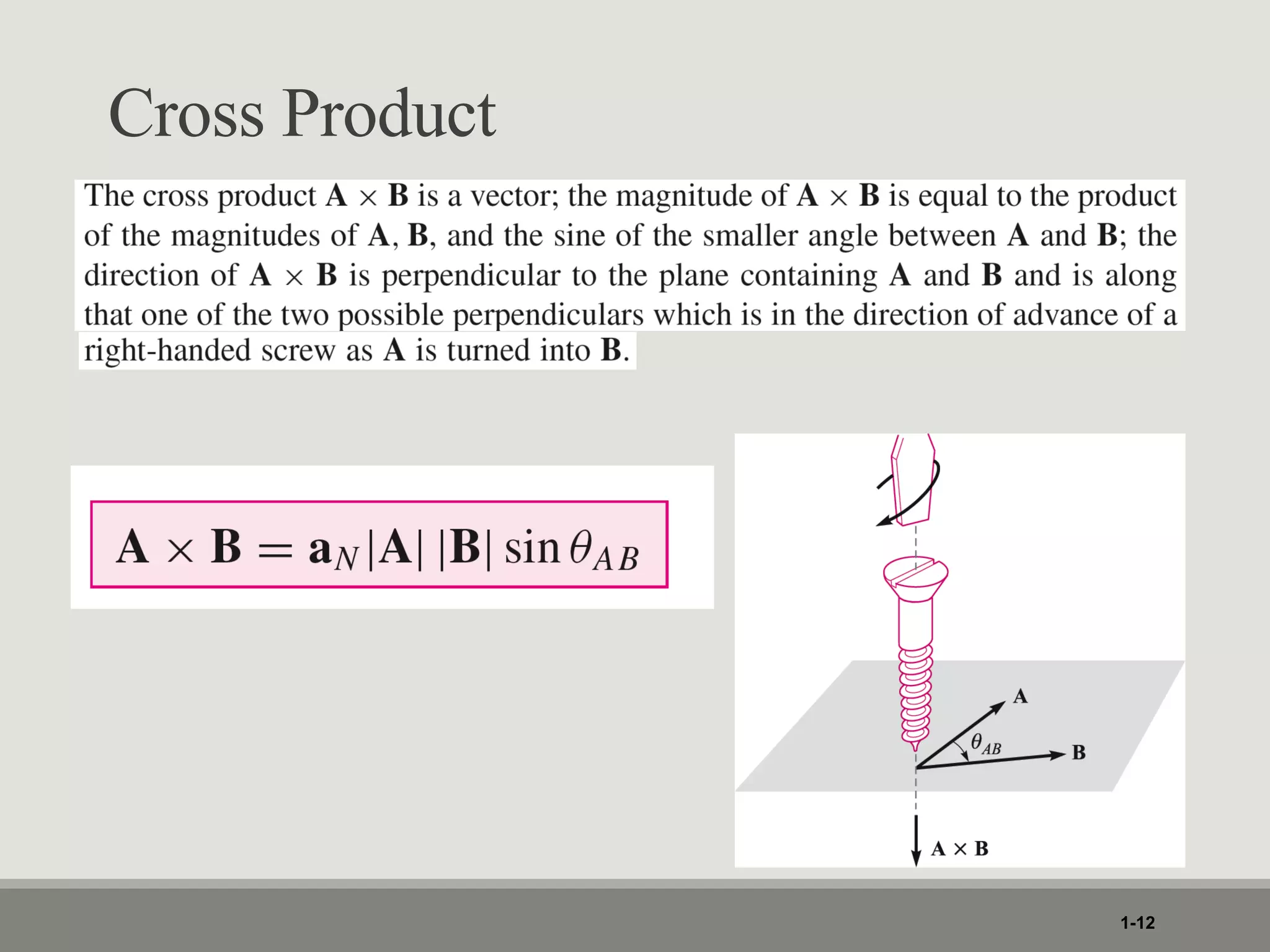
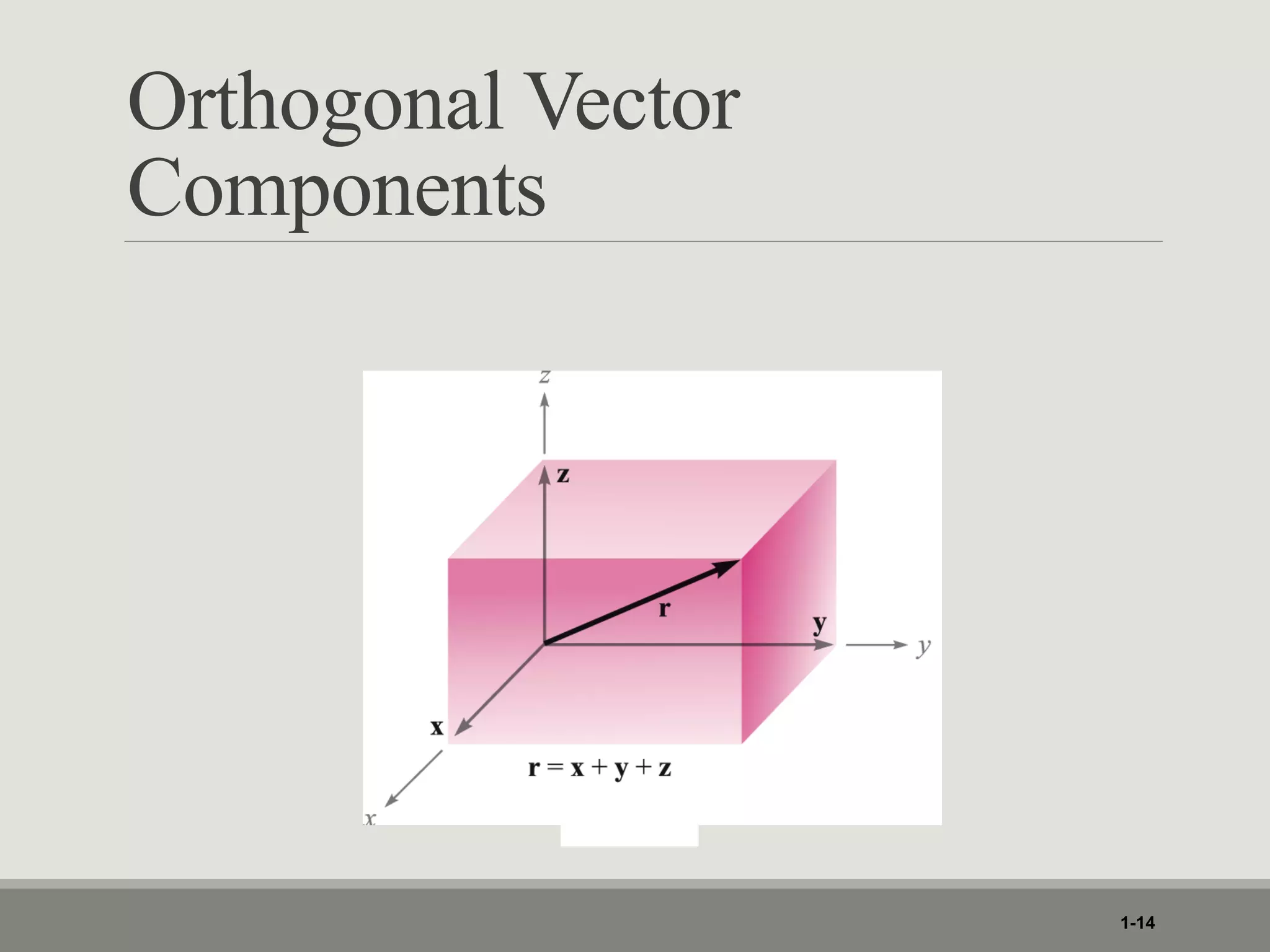
1. The document discusses different coordinate systems including rectangular, cylindrical, and spherical coordinates. It defines scalar and vector fields and provides examples. 2. Key concepts covered include the dot product, cross product, gradient, divergence, curl, and Laplacian as they relate to vector and scalar fields in different coordinate systems. 3. Various coordinate transformations are demonstrated along with differential elements, line integrals, surface integrals and volume integrals in each system.

1. Co-ordinate Systems
By,
S.T.Suganthi,
HOD/EEE,
S.Veerasamy Chettiar college of Engineering and
Technology,
Puliangudi-627855

2. Vector Calculus - Addition
1-2
Associative Law:
Distributive Law:

3. Scalar and Vector Fields
A scalar field is a function that gives us a single value of some variable
for every point in space.
◦ Examples: voltage, current, energy, temperature
A vector is a quantity which has both a magnitude and a direction in
space.
◦ Examples: velocity, momentum, acceleration and force

4. Examples of Vector Fields

5. Examples of Vector Fields

6. Examples of Vector Fields

7. Vector Field
1-7
We are accustomed to thinking of a specific vector:
A vector field is a function defined in space that has magnitude
and direction at all points:
where r = (x,y,z)

8. The Dot Product
1-8
Commutative Law:

9. Vector Projections Using the Dot Product
B • a gives the component of B
in the horizontal direction
(B • a) a gives the vector component
of B in the horizontal direction

10. Projection of a vector on another vector

11. Operational Use of the Dot Product
Given
Find
where we have used:
Note also:

12. Cross Product
1-12

13. Operational Definition of the Cross Product in
Rectangular Coordinates
Therefore:
Or…
Begin with:
where

14. Orthogonal Vector
Components
1-14

15. Orthogonal Unit Vectors
1-15

16. Vector Representation in Terms of Orthogonal
Rectangular Components
1-16

17. Co-ordinate System
To describe a vector accurately such as lengths, angles, and
projections etc…
Three types of Co-ordinate system
 Rectangular (or) Cartesian Co-ordinates
 Cylindrical Co-ordinates
 Spherical Co-ordinates
1-17

18. Rectangular Coordinate System
Co-ordinates are (x,y,z)
1-18

19. Rectangular Coordinate System
A Point Locations in Rectangular Coordinates –
Intersection of 3 orthogonal planes ( X-constant
plane, Y- constant Plane, Z-constant plane)
1-19

20. Differential Volume Element
1-20

21. Vector Expressions in Rectangular
Coordinates
1-21
General Vector, B:
Magnitude of B:
Unit Vector in the
Direction of B:

22. Example
1-22

23. Cylindrical Coordinate Systems
1-23

24. Cylindrical Coordinate Systems
1-24

25. Cylindrical Coordinate Systems
1-25

26. Cylindrical Coordinate Systems
1-26

27. Differential Volume in Cylindrical Coordinates
1-27
dV = dddz

28. Point Transformations in Cylindrical
Coordinates
1-28

29. Dot Products of Unit Vectors in Cylindrical and
Rectangular Coordinate Systems
1-29

30. Example
1-30
Transform the vector, into cylindrical coordinates:
Start with:
Then:

31. Finally:
Example: cont.

32. 1-32
Spherical Coordinates

33. 1-33
Spherical Coordinates

34. 1-34
Spherical Coordinates

35. 1-35
Spherical Coordinates

36. 1-36
Spherical Coordinates

37. Spherical Coordinates
1-37
Point P has coordinates
Specified by P(r)

38. Differential Volume in Spherical Coordinates
1-38
dV = r2sindrdd

39. Dot Products of Unit Vectors in the Spherical
and Rectangular Coordinate Systems
1-39

40. Example: Vector Component Transformation
1-40
Transform the field, , into spherical coordinates and components

41. Constant coordinate surfaces-
Cartesian system
1-41
 If we keep one of the coordinate variables
constant and allow the other two to vary,
constant coordinate surfaces are generated in
rectangular, cylindrical and spherical
coordinate systems.
 We can have infinite planes:
X=constant,
Y=constant,
Z=constant
 These surfaces are perpendicular to x, y and z axes respectively.

42. Constant coordinate surfaces-
cylindrical system
1-42
 Orthogonal surfaces in cylindrical
coordinate system can be generated as
ρ=constnt
Φ=constant
z=constant
 ρ=constant is a circular cylinder,
 Φ=constant is a semi infinite plane with its
edge along z axis
 z=constant is an infinite plane as in the
rectangular system.

43. Constant coordinate surfaces-
Spherical system
1-43
 Orthogonal surfaces in spherical
coordinate system can be generated
as
r=constant
θ=constant
Φ=constant
 θ =constant is a circular cone with z axis as its axis and origin at
the vertex,
 Φ =constant is a semi infinite plane as in the cylindrical system.
 r=constant is a sphere with its centre at the origin,

44. Differential elements in rectangular
coordinate systems
1-44

45. Differential elements in Cylindrical
coordinate systems
1-45

46. Differential elements in Spherical
coordinate systems
1-46

47. 1-47
Line integrals
 Line integral is defined as any integral that is to be evaluated
along a line. A line indicates a path along a curve in space.

48. Surface integrals
1-48

49. Volume integrals
1-49

50. DEL Operator
1-50
 DEL Operator in cylindrical coordinates:
 DEL Operator in spherical coordinates:

51. Gradient of a scalar field
1-51
 The gradient of a scalar field V is a vector that represents the
magnitude and direction of the maximum space rate of increase of V.
 For Cartesian Coordinates
 For Cylindrical Coordinates
 For Spherical Coordinates

52. Divergence of a vector
1-52
 In Cartesian Coordinates:
 In Cylindrical Coordinates:
 In Spherical Coordinates:

53. Gauss’s Divergence theorem
1-53

54. Curl of a vector
1-54

55. Curl of a vector
1-55
 In Cartesian Coordinates:
 In Cylindrical Coordinates:
 In Spherical Coordinates:

57. Stoke’s theorem
1-57

58. Laplacian of a scalar
1-58

59. Laplacian of a scalar
1-59