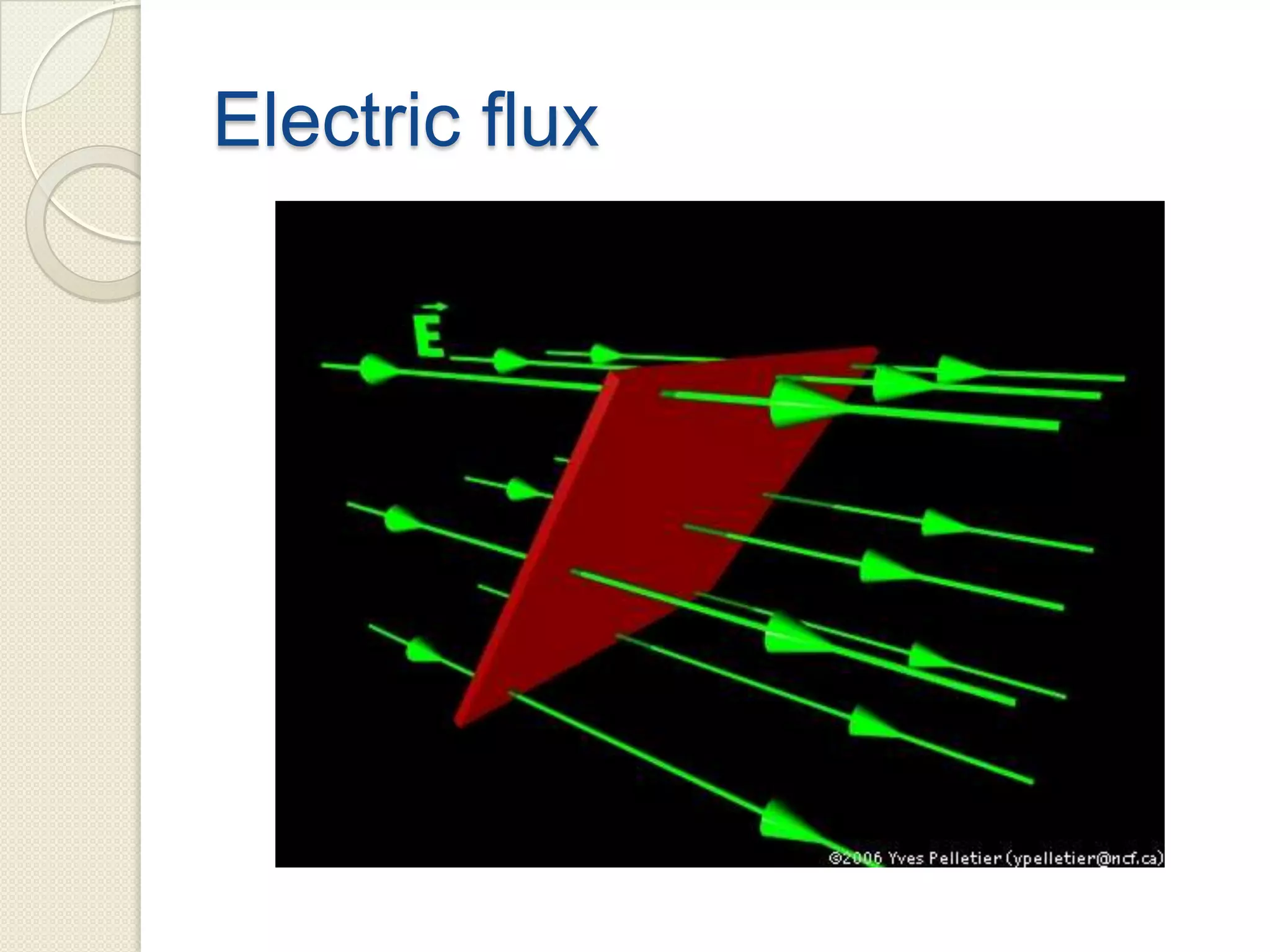
Divergence is a mathematical operation on a vector field that calculates the density of the vector field's source at a given point. It measures the flux of a vector field out of an infinitesimally small volume element at that point. Divergence equals flux per unit volume, so a positive divergence means flux is spreading out from the point and a negative divergence means flux is converging at the point. Divergence can be represented in Cartesian, cylindrical, or spherical coordinate systems using partial derivatives and the del operator.

1. DIVERGENCE
BY : SHAKIR HUSSAIN
B.E-IV

2. What is flux
• The flow of energy through a surface.
• In electronics, the term applies to
any electrostatic field and
any magnetic field . Flux is called as
"lines" in a plane that contains or
intersects electric charge poles or
magnetic poles.

3. Electric flux

4. Magnetic flux

5. WHAT IS DIVERGENCE
 Divergence is an operation which is
performed on vector and that results in
scalar quantity.
 It tells how much flux is entering or
leaving a small volume(or a point) per
unit volume.
 divergence is just the net flux per unit
volume, or “flux density”.
◦ Divergence = Flux / Volume.
• It states that the sum of all sources minus
the sum of all sinks gives the net flow out of a

6. Types of Divergence
 Zero Divergence
◦ No net flux inside the region or volume.

7. Types of Divergence
 POSITIVE DIVERGENCE
◦ Divergence of vector field is positive if
vector diverges or spread out from given
point.

8. Types of Divergence
 Negative Divergence
◦ Divergence of vector field is called
negative if vector converges at that given
point.

9. Divergence of Vector Field
 Divergence of vector field A is measure of
how much a vector field converges to or
diverges from a given point in volume.
 The divergence of a vector field A is
defined
as
Div A= A

10. DEL OPERATOR
 "del operator", usually denoted by the
symbol (which is called the
"nabla"). This can be regarded as a
vector whose components in the three
principle directions of a Cartesian
coordinate system(or any other) are
partial differentiations with respect to
those three directions(x,y,z) or any
other

11. DEL OPERATOR
 the del operator can be expressed as
Letting i, j, k denote the basis vectors in
the x,y,z directions.

12. Methamatical representation
Divergence
 Total flux change = (field change in X direction)
+ (field change in Y direction) + (field change in
Z direction)
Assuming F1 is the field in the X direction, F2 in
the Y and F3 in the Z.

13. Methamatical representation
In Cylinderical Form
In the above Divergence of vector A is
in cylinderical form.

14. Methamatical representation
In Spherical Form
In the above Divergence of vector A is
repersented in Spherical form.