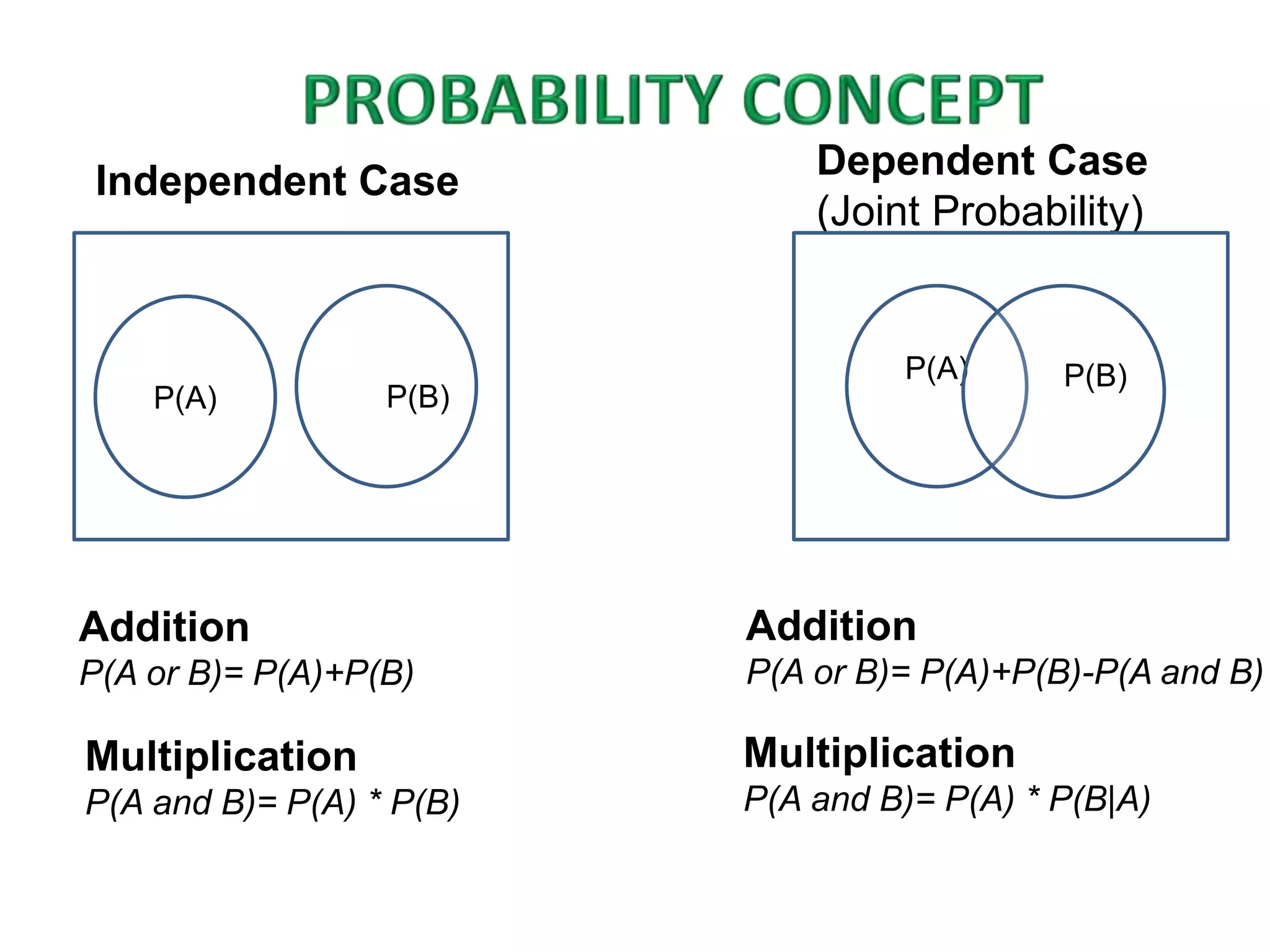
This document defines key probability concepts like experiment, outcome, event, joint probability, and conditional probability. It then uses Bayes' Theorem to calculate the posterior probability that a defective chip was manufactured by one of three suppliers (Schuller Sales) given the prior probabilities and conditional probabilities of defects from each supplier. The probability is calculated to be 25.64% that the defective chip came from Schuller Sales.

2. • Probability= Likelihood= Chance
• Three Term
(1)Experiment
A process that leads to the occurrence of one(and only one) of
several possible observation. (eg- tossing a coin, microscope=>2 or more
possible result)
Experiment Outcome
(2)Outcome
A particular result of the experiment. (eg – tossing a coin => head & tail)
(3)Event
A collection of one of more outcomes of an experiment.
1st time=> 200 people tossing a coin
2nd time => 500 people tossing a coin

3. Independent Case
Dependent Case
(Joint Probability)
P(A)
Addition
P(A or B)= P(A)+P(B)
P(A)
Multiplication
P(A and B)= P(A) * P(B)
Addition
P(A or B)= P(A)+P(B)-P(A and B)
Multiplication
P(A and B)= P(A) * P(B|A)
P(B)
P(B)

4. Joint Probability
• Joint Probability is the likelihood that two or more events
will happen at the same time.
Conditional Probability
• A conditional probability is the likelihood that an event
will happen given that another event has already
happened.

5. In the 18th Century , Reverend Thomas Bayes, an English
Presbyterian minister, ponder this question:
“Does God really exist?”
Being interested in the mathematics, he attempt to develop a
formula to arrive at the probability that God does exist based on
the evidence that was available to him on earth.
Later, Laplace refined Bayes’ work and gave it the name
“Bayes’ Theorem”.

6. Bayes’ Theorem is a method of revising a probability,
given that additional information is obtained. For two event:
P(A1|B)=P(A1) P(B|A1)
P(A1)P(B|A1)+P(A2)P(B|A2)
Prior Probability
The initial Probability based on the present level of
information.
Posterior Probability
A revised Prabability based on additional information.

7. • The manufacturer of VCR purchase LS-24 chip from the three
suppliers called Hall Electronic, Schuller Sales and Crawford
component.
• 30 % of LS-24 chip are purchased from Hall Electronic.
• 20% of LS-24 chip are purchased from Schuller Sales .
• 50% of LS-24 chip are purchased from Crawford Component.
• The manufacturer has the extensive history with the three
suppliers and know that 3 % of LS-24 chip from Hall
Electronic are defective .

8. • 5 % of LS-24 chip from Schuller Sales are defective.
• 4 % of LS-24 chip from Crawford Component are
defective.
• When the LS-24 chips are arrive at the manufacturer,
they are placed directly in a bin and not inspected.
• A worker selects a chip for installation and finds it
defective.
• What is a probability that it was
manufactured by Schuller Sale?

9. There are three event, that is , three supplier
A1= The LS-24 was purchased from Hall Electronics
A2= The LS-24 was purchased from Schuller Electronics
A3= The LS-24 was purchased from Crawford Component
Prior Probabilities
P(A1)= .30 => The probability the LS-24 was manufactured by Hall
Electronic
P(A2)= .20 => The probability the LS-24 was manufactured by Schuller
Electronic
P(A3)=.50 => The probability the LS-24 was manufactured by Crawford
Component
The additional information is that the LS-24 chip is defective.
B1 => The LS-24 is defective.
B2 => The LS-24 is not defective

10. The following conditional probabilities are given
P(B1| A1)=.03 The probability that an LS-24 chip produced
by Hall Electronic is defective.
P(B1| A2)=.05 The probability that an LS-24 chip produced
by Schuller Sales is defective.
P(B1| A3)=.04 The probability that an LS-24 chip produced
by Crawford Component is defective.

11. Conditional
Probability
Prior
Probability
Probability
P(A1)=.30
P(B1|A1)=.03
P(B2|A1)=.97
P(A2)=.20
P(B1|A2)=.05
P(B2|A2)=.95
P(A3)=.50
P(B1|A3)=.04
P(B2|A3)=.96
Joint Probability
A1= Hall Electronic
A2= Schuller Electronics
A3= Crawford Component
B1= Defective
B2=Good
P(A1 and B1)
=P(A1)P(B1|A1)
=.30x.03=.009
P(A1 and B2)
=P(A1)P(B2|A1)
=.30x.97=.291
P(A2 and B1)
=P(A2)P(B1|A2)
=.20x.05=.010
P(A2 and B2)
=P(A2)P(B2|A2)
=.20x.95=.190
P(A3and B1)
=P(A3)P(B1|A3)
=.50x.04=.020
P(A3 and B2)
=P(A3)P(B2|A3)
=.20x.95=.480

12. Event
(Ai)
Prior Probability
(P(Ai))
Conditional
Probability
(P(Bi| Ai)
Joint
Probability
P(Ai and Bi)
Posterior
Probability
P(Ai|Bi)
Hall .30 .03 .009 .009/.039=.2308
Schuller .40 .05 .010 .010/.039=.2564
Crawford .50 .04 .020 .020/.039=.5128
P(Bi)= .039 1.0000
Defective chip probability was manufactured by Schuller Sale=.2564(26%)