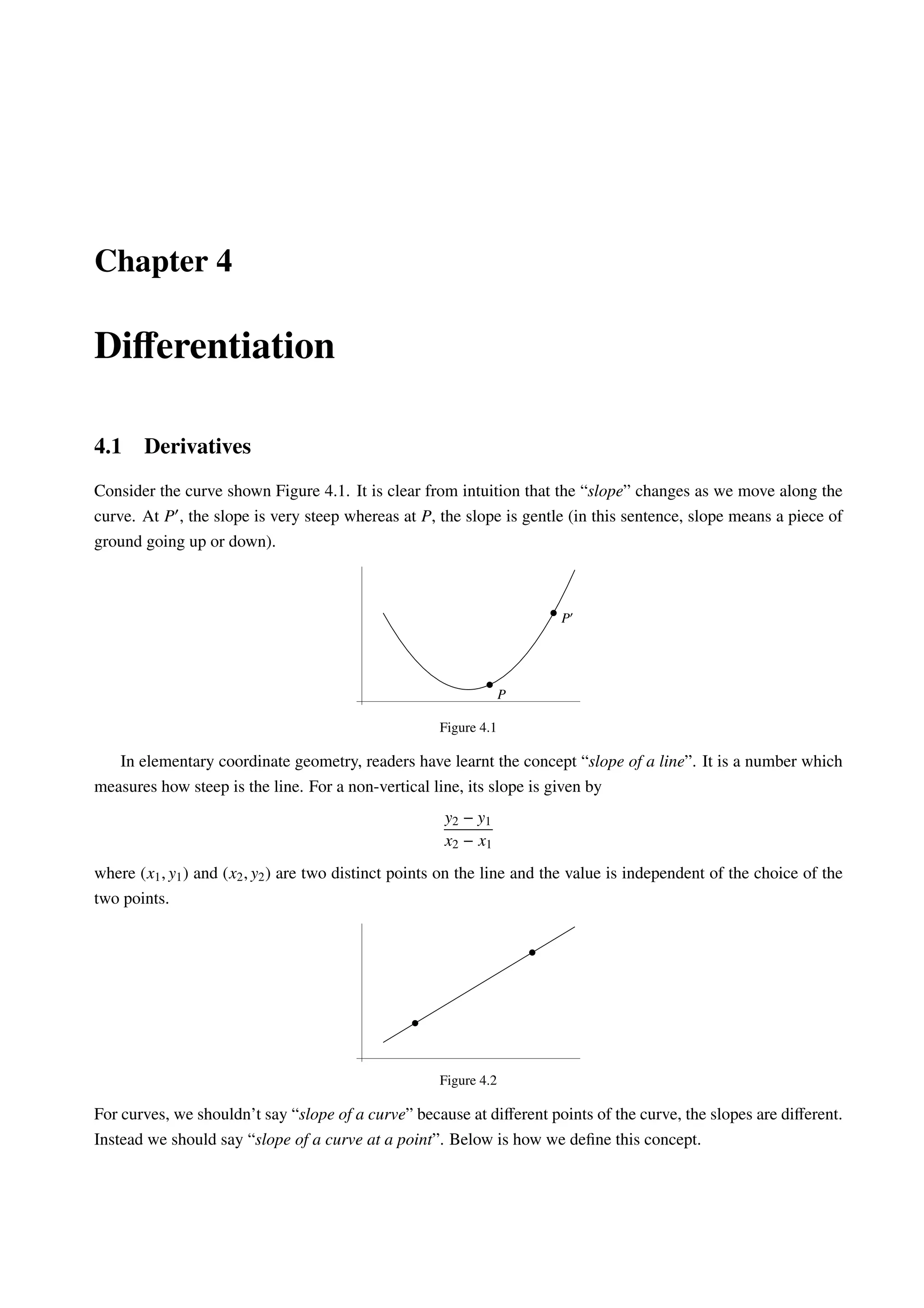
This document discusses the concept of the derivative and differentiation. It begins by explaining how the slope of a curve changes at different points, unlike the constant slope of a line. It then defines the derivative of a function f at a point x0 as the limit of the difference quotient as h approaches 0. If this limit exists, then f is said to be differentiable at x0. The derivative f'(x) then represents the slope of the curve y=f(x) at each point x and is a measure of how steeply the curve is rising or falling at that point. Several examples are provided to illustrate how to compute derivatives using this limit definition.