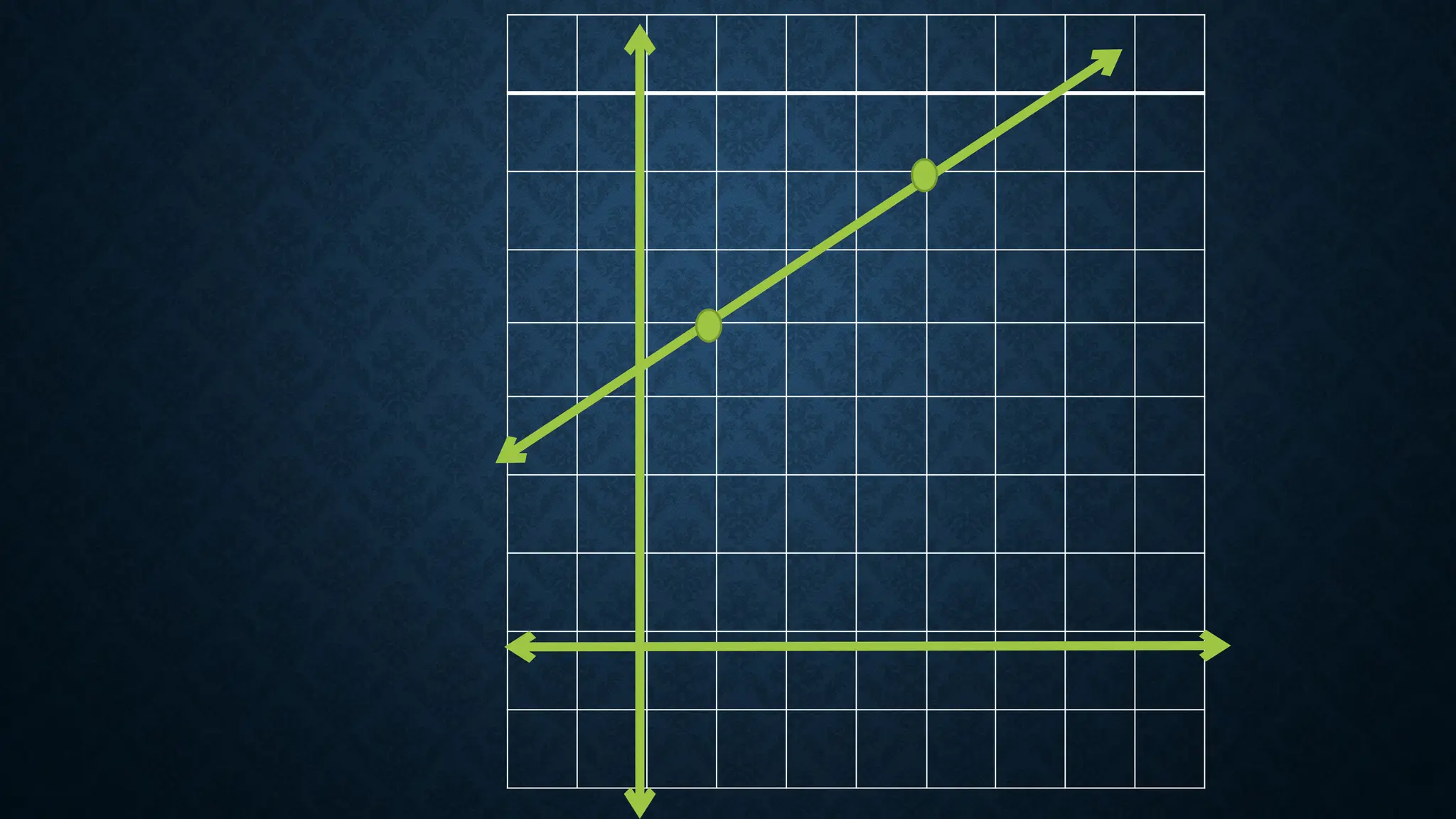
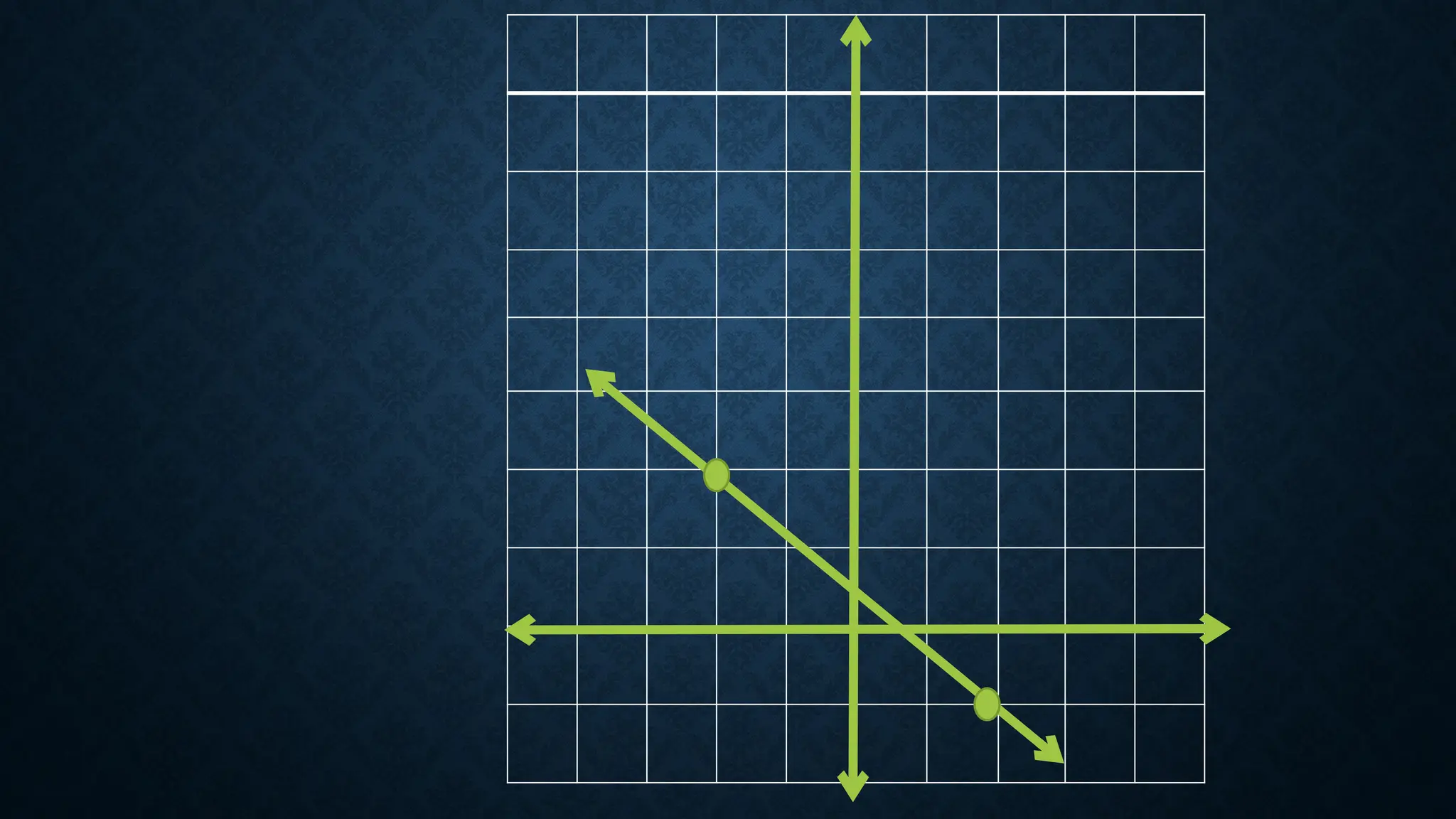
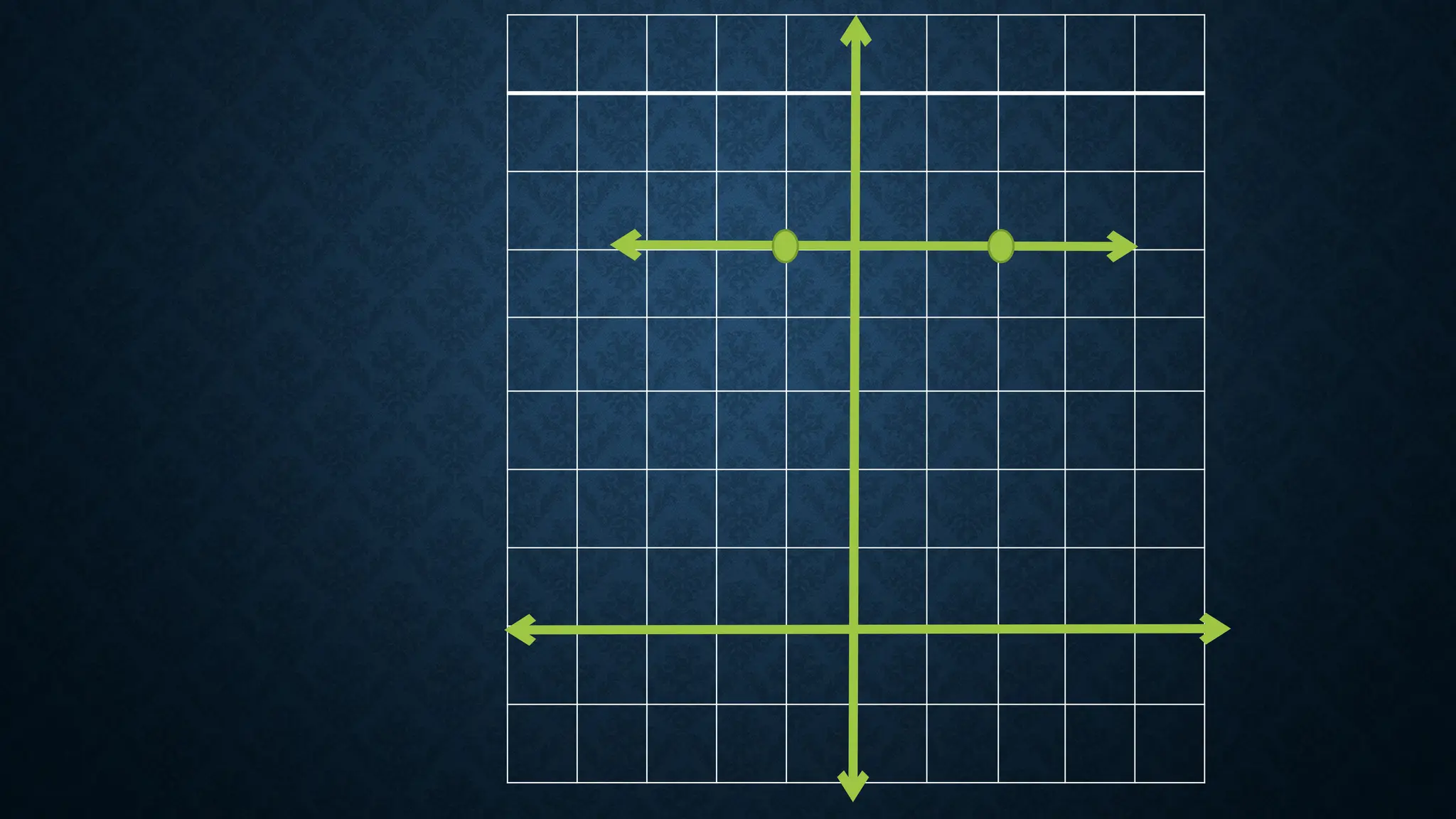
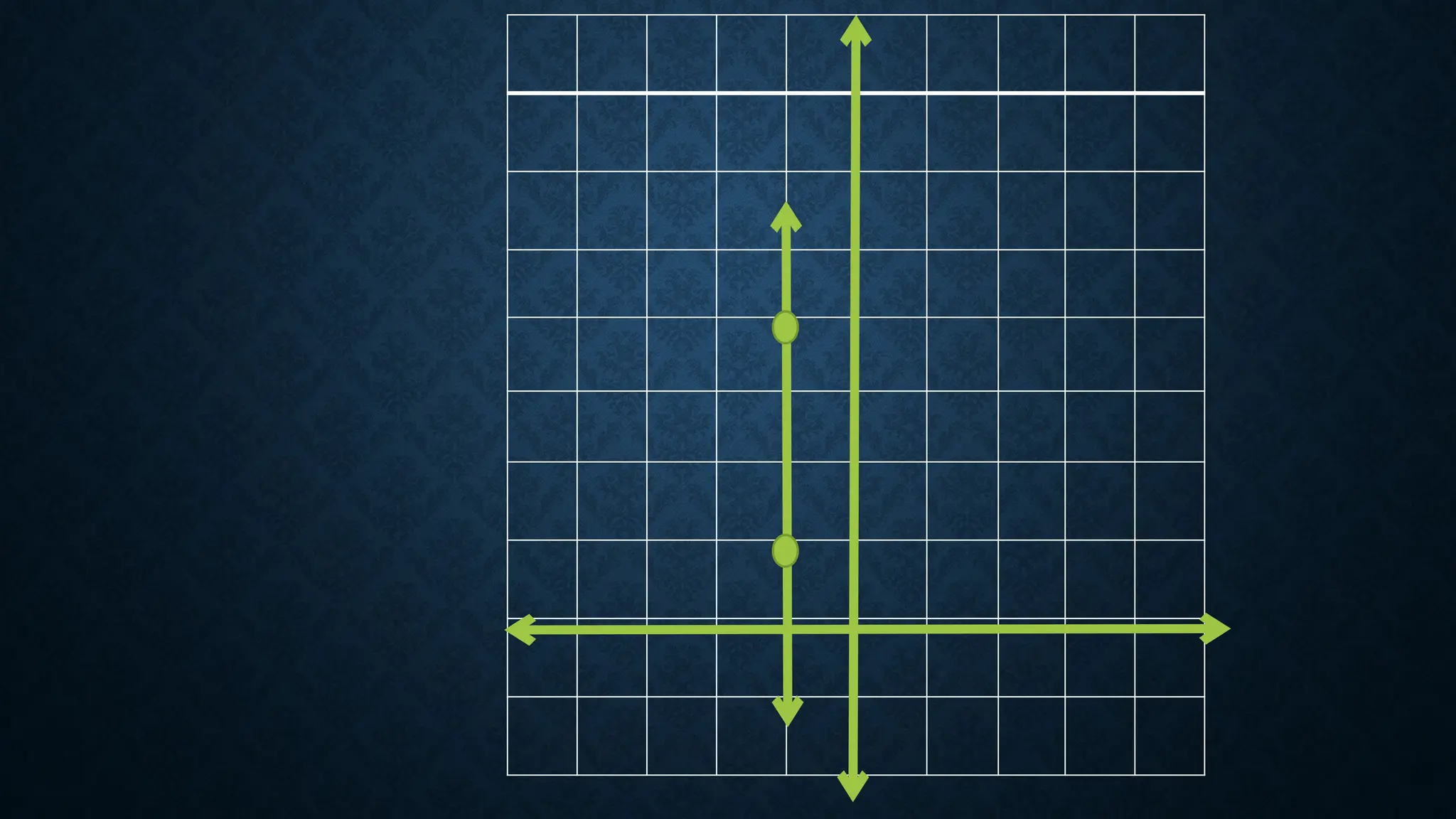
The document defines linear functions as equations of the form f(x) = ax + b and provides examples to determine if specific functions are linear. It explains slope, including how to calculate it and its significance in graphing, and discusses different types of slopes (positive, negative, zero, and undefined). Examples are provided for finding slope between points and for determining values to achieve a given slope.

1. GRAPHING OF LINEAR
EQUATIONS

2. DEFINITION:
Linear Function
A linear function is a function
whose equation can be written in
the form f(x) = ax + b, where a
and b are real numbers .

3. Example:
State whether or not each function is
a linear function.
a. f (x) = 4x + 5
b. g (x) = x2
- 1
c. h (x) = 9-5x
d. h(x) = 8 -9x
e. f (x) = 2x -7 f. g (x) = x2
+ 3

4. Discussion:
The graph of the linear function f(x) = ax + b
is exactly the same as the graph of the linear
equation y= ax + b. If a=0, then we get f(x) =
b, which is called a constant function. If a =1
and b=0 , then we get the function f(x) = x
which is called the identity function.

5. SLOPE:
The slope m of a line is the
ratio of the change in the y-
coordinates to the
corresponding change in the
x-coordinates.

10. Note:
1.The graph in a slopes upward
from left to right has a positive
slope.
2.The graph in b slopes
downward from left to right and
has a negative slope.

11. Note:
3.The graph in c is a horizontal
line and has a slope of zero.
4.The graph in d is a vertical line
and its slope is undefined.

12. Rule: Determining Slope
If the coordinates of two points on a
line are (x1, y1) and (x2, y2), the slope
m can be found as follows:
𝑚=
𝑦 2− 𝑦 1
𝑥 2− 𝑥 1
, where x1 x2

13. Example:
Find the slope of the line
containing each pair of points.
a. (-2, 1) and (4,6)
b. (-1, 5) and (2, 5)
c. (-3, 3) and (2, -2)
d. (-2, 6) and (-2, 2)

14. Example:
Determine the value of n so the line that
passes through each pair of points has the
given slope .
a. (2, 1) and (n, 5); m=
b. (-5, n) and (5, 1); m=