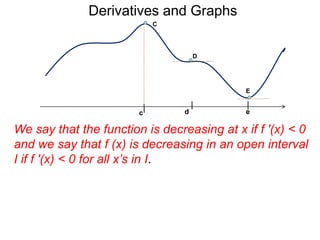
The document discusses derivatives and graphs. It defines interval notation used to indicate whether points are included or excluded from intervals. It then explains that the derivative of a function f(x) at a point x, f'(x), represents the slope of the tangent line to the graph of f(x) at (x, f(x)). Finally, it notes that points where the derivative is 0 are called critical points, as the tangent line is flat at these points.

![Derivatives and Graphs
Interval Notation
We use “(” and “)” to indicate the corresponding point is
excluded and we use “[” and “]” to for the inclusion of the point.
a < x < b
(a, b)
a b
a closed interval:
a ≤ x ≤ b
a b
a ≤ x < b
a [a, b) b
[a, b]
a < x ≤ b
a b
(a, b]
For the unbounded intervals, use “(” or “) for ±∞,
for example, “(–∞, a] or (a, ∞) are the following intervals.
x < a
(–∞, a] a
–∞
a < x
a ∞
an open interval:
half–open intervals:](https://image.slidesharecdn.com/3-4derivativeandgraphs-120320093444-phpapp02/85/3-4-derivative-and-graphs-2-320.jpg)

































































![Derivatives and Graphs
At a maximum point the graph must be
changing from going uphill to going downhill
and at the minimum point it must be changing
from going downhill to uphill. Hence the signs
of the y' must change at these critical points.
up down
down up
Both f(x) = x3(3 – x)(3 + x) = x3(9 – x2) = 9x3 – x5 and
g(x) = x(9 – x2) have the same sign–chart so both
graphs are similar.
However, for f(x) it’s derivative
f '(x) = [9x3 – x5 ]' = 27x2 – 5x4 = x2(27 – 5x2).
Max
Min](https://image.slidesharecdn.com/3-4derivativeandgraphs-120320093444-phpapp02/85/3-4-derivative-and-graphs-69-320.jpg)
![Derivatives and Graphs
At a maximum point the graph must be
changing from going uphill to going downhill
and at the minimum point it must be changing
from going downhill to uphill. Hence the signs
of the y' must change at these critical points.
up down
down up
Both f(x) = x3(3 – x)(3 + x) = x3(9 – x2) = 9x3 – x5 and
g(x) = x(9 – x2) have the same sign–chart so both
graphs are similar.
However, for f(x) it’s derivative
f '(x) = [9x3 – x5 ]' = 27x2 – 5x4 = x2(27 – 5x2).
signs around x = 0 of
f '(x) = x2(27 – 5x2)
+ uphill
+ uphill
f '(0)=0 with order 2
Max
Min](https://image.slidesharecdn.com/3-4derivativeandgraphs-120320093444-phpapp02/85/3-4-derivative-and-graphs-70-320.jpg)
![Derivatives and Graphs
At a maximum point the graph must be
changing from going uphill to going downhill
and at the minimum point it must be changing
from going downhill to uphill. Hence the signs
of the y' must change at these critical points.
Max
up down
down up
Min
Both f(x) = x3(3 – x)(3 + x) = x3(9 – x2) = 9x3 – x5 and
g(x) = x(9 – x2) have the same sign–chart so both
graphs are similar.
However, for f(x) it’s derivative
f '(x) = [9x3 – x5 ]' = 27x2 – 5x4 = x2(27 – 5x2).
+ uphill
+ uphill
f '(0)=0 with order 2
signs around x = 0 of
f '(x) = x2(27 – 5x2)
The sign of f '(x) is positive on both sides of x = 0,
so (0, 0) is not a max nor min, it’s a flat landing point.](https://image.slidesharecdn.com/3-4derivativeandgraphs-120320093444-phpapp02/85/3-4-derivative-and-graphs-71-320.jpg)















