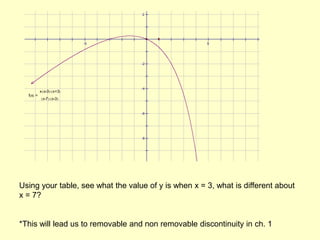
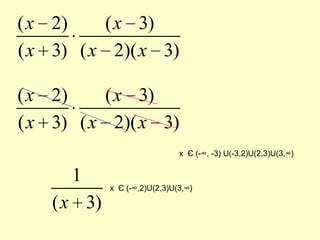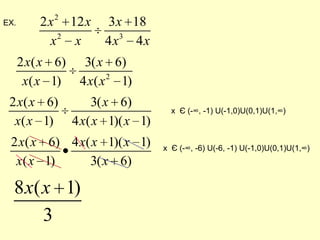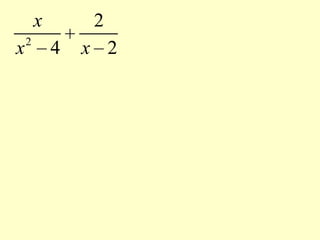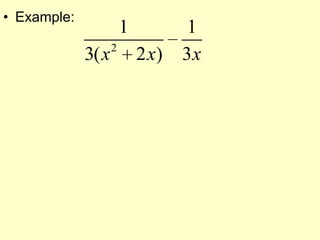Rational expressions are fractions with polynomials in the numerator and denominator. The domain of a rational expression excludes values that would make the denominator equal to zero, as division by zero is undefined. To simplify rational expressions, factor the numerator and denominator and reduce where possible. When combining rational expressions through addition, subtraction, multiplication or division, the key steps are to factor denominators, find the common domain, and reduce. Rationalizing techniques include using the conjugate or rationalizing the numerator.

1. 0.5 Rational ExpressionsGoal: To Simplify and rationalize the denominator of rational expressions.Rational Expression:A rational expression is fraction whose numerator and denominator are polynomialsFor example:

2. Rational Functions:Let u(x) and v(x) be polynomial functions. The function Is a rational function. The domain of this rational expression is the set of all real numbers for which v(x) ≠ 0.

3. The key issue with the domain of rational expressions is that we can never divide by zero.Recall: Dividing by zero is undefinedex.Domain = (-∞,0) U (0,∞)

4. Example:Domain = (-∞,3) U (3,7) U (7,∞)Whenever we work with rational expressions, we have to make sure we check the domain. We never want to have an answer that results in the function becoming undefined.

5. Find the domain(-∞,2) U (2, ∞)Find the domain(-∞,1) U (1, ∞)To simplify rational expressions:Factor both numerator and denominatorFind domain of denominatorReduce where possibleExample:(-∞, 3)U(3,7)U(7,∞) is the domain of the denominator(-∞, 3)U(3,∞) We list this as our domain restriction since we have canceled the factor (x-3) on the graph there is a whole at x = 3

6. Using your table, see what the value of y is when x = 3, what is different about x = 7? *This will lead us to removable and non removable discontinuity in ch. 1

7. Example: Simplify(-∞, 0)U(0,1)U(1,∞) is the domain of the denominatorx Є(-∞, 0)U(0,1)U(1,∞)

8. To Multiply/Divide rational expressions:

9. Factor both numerator and denominator

10. Find domain of denominator for both expressions (also denominator of reciprocal when you divide)

11. Reduce where possible

12. Example:x Є(-∞, -3) U(-3,2)U(2,3)U(3,∞) x Є(-∞,2)U(2,3)U(3,∞)

13. EX.x Є(-∞, -1) U(-1,0)U(0,1)U(1,∞) x Є(-∞, -6) U(-6, -1) U(-1,0)U(0,1)U(1,∞)

14. To Add/Subtract rational expressions:

15. Factor denominators

16. Find domain of denominator for both expressions

17. Reduce where possible