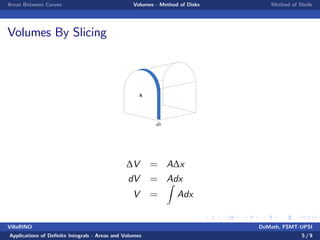
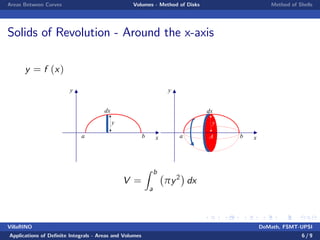
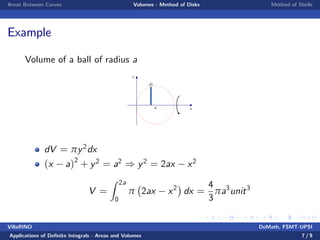
This document discusses using definite integrals to calculate areas and volumes. It introduces two methods for finding volumes: the disk method, which slices a solid into thin disks, and the shell method, which slices into thin cylindrical shells. Examples are provided for finding the volume of a sphere using both methods and calculating the area between two curves.

1. Beginning Calculus
Applications of De…nite Integrals - Areas and Volumes -
Shahrizal Shamsuddin Norashiqin Mohd Idrus
Department of Mathematics,
FSMT - UPSI
(LECTURE SLIDES SERIES)
VillaRINO DoMath, FSMT-UPSI
Applications of De…nite Integrals - Areas and Volumes 1 / 9

2. Areas Between Curves Volumes - Method of Disks Method of Shells
Learning Outcomes
Compute the areas between to curves.
Use disk or shell methods to compute volumes.
VillaRINO DoMath, FSMT-UPSI
Applications of De…nite Integrals - Areas and Volumes 2 / 9

3. Areas Between Curves Volumes - Method of Disks Method of Shells
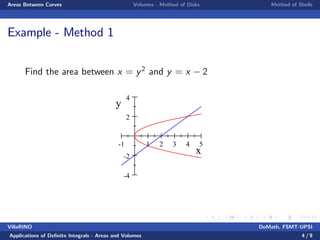
Area Between Curves
y
x
dx
a b
f(x)
g(x)
A =
Z b
a
[f (x) g (x)] dx
VillaRINO DoMath, FSMT-UPSI
Applications of De…nite Integrals - Areas and Volumes 3 / 9

4. Areas Between Curves Volumes - Method of Disks Method of Shells
Example - Method 1
Find the area between x = y2 and y = x 2
-1 1 2 3 4 5
-4
-2
2
4
x
y
VillaRINO DoMath, FSMT-UPSI
Applications of De…nite Integrals - Areas and Volumes 4 / 9

5. Areas Between Curves Volumes - Method of Disks Method of Shells
Volumes By Slicing
A
dx
∆V = A∆x
dV = Adx
V =
Z
Adx
VillaRINO DoMath, FSMT-UPSI
Applications of De…nite Integrals - Areas and Volumes 5 / 9

6. Areas Between Curves Volumes - Method of Disks Method of Shells
Solids of Revolution - Around the x-axis
y = f (x)
y
xa b
dx
y
y
xa b
y
dx
A
V =
Z b
a
πy2
dx
VillaRINO DoMath, FSMT-UPSI
Applications of De…nite Integrals - Areas and Volumes 6 / 9

7. Areas Between Curves Volumes - Method of Disks Method of Shells
Example
Volume of a ball of radius a
y
xa
dx
dV = πy2dx
(x a)2
+ y2 = a2 ) y2 = 2ax x2
V =
Z 2a
0
π 2ax x2
dx =
4
3
πa3
unit3
VillaRINO DoMath, FSMT-UPSI
Applications of De…nite Integrals - Areas and Volumes 7 / 9

8. Areas Between Curves Volumes - Method of Disks Method of Shells
Example - continue
V (x) := volume of portion of width x of ball.
x
V(x)
V (x) = π ax2 x3
3
(Check) . If x = a, then
V (x) = π a3 a3
3
=
2
3
πa3
unit3
VillaRINO DoMath, FSMT-UPSI
Applications of De…nite Integrals - Areas and Volumes 8 / 9

9. Areas Between Curves Volumes - Method of Disks Method of Shells
Solid of Revolution - Around the y-axis
y
x
y = x2
y = a dx
y
x
y
x
y
x
dx
y
x
y
x
dx
Thickness := dx
Height := ytop ybottom = a y = a x2
Circumference := 2πx
dV = (2πx) a x2
dx = 2π ax x3
dx
V =
Z p
a
0
2π ax x3
dx =
1
2
πa2
unit3
VillaRINO DoMath, FSMT-UPSI
Applications of De…nite Integrals - Areas and Volumes 9 / 9