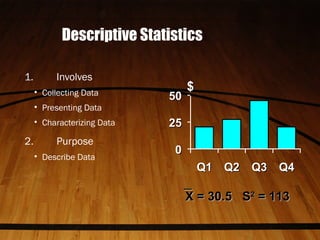
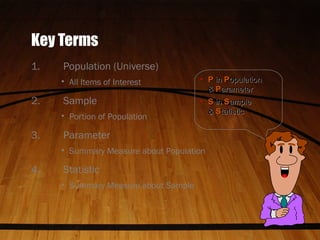
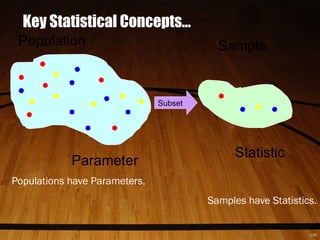
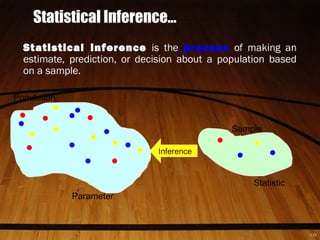
Statistics is the science of collecting, organizing, presenting, analyzing, and interpreting numerical data. It helps make better decisions by extracting information from data. There are two main types: descriptive statistics which describe data through methods like averages and distributions, and inferential statistics which make estimates, predictions, or generalizations about a population based on a sample. Key concepts in statistics include populations, samples, parameters which describe populations, and statistics which describe samples. The level of measurement of data, such as nominal, ordinal, interval, or ratio, determines what calculations and tests can be done.

1. What is Statistics?
K.THIYAGU
thiyagusuri@gmail.com
surithiyagu@gmail.com

2. Learning Objectives
1. Define Statistics
2. Describe the Uses of Statistics
3. Distinguish Descriptive & Inferential Statistics
4. Define Population, Sample, Parameter,
& Statistic

3. 1.3
What is Statistics?
“Statistics is a way to get information from data”
Data
Statistics
Information
Data: Facts, especially
numerical facts, collected
together for reference or
information.
Information:
Knowledge
communicated
concerning some
particular fact.
Statistics is a tool for creating new understanding from a set of numbers.

4. Meaning
•Statistics appears to have
been derived from the Latin
‘status’ meaning a state.
23/07/14Thiyagu..........measurement scale

5. 23/07/14Thiyagu..........measurement scale
Statistics
• Statistics techniques used to collect, organize,
present, analyse, and interpret data to make
better decisions.

6. What is Meant by Statistics?
Statistics is the science of
collecting, organizing,
presenting, analyzing, and
interpreting numerical data to
assist in making more effective
decisions.

7. Why Study Statistics?
1. Numerical information is everywhere
2. Statistical techniques are used to make decisions
that affect our daily lives

8. Who Uses Statistics?
Statistical techniques are used
extensively by marketing,
accounting, quality control,
consumers, professional sports
people, hospital administrators,
educators, politicians, physicians,
etc...

9. Statistical Methods
Statistical
Methods
Descriptive
Statistics
Inferential
Statistics

10. Descriptive Statistics
1. Involves
• Collecting Data
• Presenting Data
• Characterizing Data
2. Purpose
• Describe Data
X = 30.5 SX = 30.5 S22
= 113= 113
00
2525
5050
Q1Q1 Q2Q2 Q3Q3 Q4Q4
$$

11. Inferential Statistics
1. Involves
• Estimation
• Hypothesis
Testing
2. Purpose
• Make Decisions About Population
Characteristics
Population?Population?

12. Key Terms
1. Population (Universe)
• All Items of Interest
2. Sample
• Portion of Population
3. Parameter
• Summary Measure about Population
4. Statistic
• Summary Measure about Sample

13. Key Terms
1. Population (Universe)
• All Items of Interest
2. Sample
• Portion of Population
3. Parameter
• Summary Measure about Population
4. Statistic
• Summary Measure about Sample
• PP inin PPopulationopulation
&& PParameterarameter
• SS inin SSampleample
&& SStatistictatistic

14. Statistical
Computer Packages
Typical Software
• SAS
• SPSS
• MINITAB
• Excel

15. Types of Statistics – Descriptive Statistics and
Inferential Statistics
Descriptive Statistics - methods of organizing, summarizing,
and presenting data in an informative way.
EXAMPLE 1: The United States government reports the population of the United
States was 179,323,000 in 1960; 203,302,000 in 1970; 226,542,000 in
1980; 248,709,000 in 1990, and 265,000,000 in 2000.
EXAMPLE 2: According to the Bureau of Labor Statistics, the average hourly
earnings of production workers was $17.90 for April 2008.

16. Types of Statistics – Descriptive Statistics and
Inferential Statistics
Inferential Statistics: A decision, estimate, prediction, or
generalization about a population, based on a sample.
Note: In statistics the word population and sample have a broader
meaning. A population or sample may consist of individuals or
objects

17. Population versus Sample
A population is a collection of all possible individuals, objects, or
measurements of interest.
A sample is a portion, or part, of the population of interest

18. 1.18
Key Statistical Concepts…
Population
— a population is the group of all items of
interest to a statistics practitioner.
— frequently very large; sometimes infinite.
E.g. All 5 million Florida voters, per Example 12.5
Sample
— A sample is a set of data drawn from the
population.
— Potentially very large, but less than the
population.
E.g. a sample of 765 voters exit polled on election day.

19. Key Statistical Concepts…
Parameter
— A descriptive measure of a population.
Statistic
— A descriptive measure of a sample.
1.19

20. Key Statistical Concepts…
Populations have Parameters,
Samples have Statistics.
1.20
Parameter
Population Sample
Statistic
Subset

21. Statistical Inference…
Statistical inference is the process of making an
estimate, prediction, or decision about a population based
on a sample.
1.21
Parameter
Population
Sample
Statistic
Inference

22. 23/07/14Thiyagu..........measurement scale
MEASUREMENT SCALES
•Nominal scale
•Ordinal scale
•Interval scale
•Ratio scale
Stevents (1946) has recognized some types of scales

23. 23/07/14Thiyagu..........measurement scale
NOMINAL SCALE
•Simple classification of
objects or items into discrete
groups.
•Eg. Naming of streets, naming
of persons and cars

24. 23/07/14Thiyagu..........measurement scale
ORDINAL SCALE
• Scale involving ranking of objects,
persons, traits, or abilities without
regard to equality of difference.
• Eg. Line up the students of a class
according to height or merits.

25. 23/07/14Thiyagu..........measurement scale
INTERVAL SCALE
• Interval scales are also called equal
unit scales.
• Scale having equal difference
between successive categories
• Eg. Intelligence scores, personality scores

26. 23/07/14Thiyagu..........measurement scale
RATIO SCALE
• Scale having an absolute zero, magnitude and
equal intervals
• Eg. Height , weight, number of students in
various class

27. 23/07/14Thiyagu..........measurement scale
Measurement scale
SCALE MAGNITUDE EQUAL
INTERVALS
ABSOLUTE
ZERO
NOMINAL
X X X
ORDINAL
√ X X
INTERVAL
√ √ X
RATIO
√ √ √

28. Four Levels of Measurement
Nominal level - data that is
classified into categories and
cannot be arranged in any
particular order.
EXAMPLES: eye color, gender, religious
affiliation.
Ordinal level – data arranged in
some order, but the differences
between data values cannot be
determined or are meaningless.
EXAMPLE: During a taste test of 4 soft drinks,
Mellow Yellow was ranked number 1,
Sprite number 2, Seven-up number 3, and
Orange Crush number 4.
Interval level - similar to the ordinal
level, with the additional property that
meaningful amounts of differences
between data values can be
determined. There is no natural zero
point.
EXAMPLE: Temperature on the
Fahrenheit scale.
Ratio level - the interval level with an
inherent zero starting point.
Differences and ratios are meaningful
for this level of measurement.
EXAMPLES: Monthly income of surgeons, or
distance traveled by manufacturer’s
representatives per month.

29. Nominal-Level Data
Properties:
1.Observations of a qualitative variable can only be
classified and counted.
2.There is no particular order to the labels.

30. Ordinal-Level Data
Properties:
1.Data classifications are represented
by sets of labels or names (high,
medium, low) that have relative
values.
2.Because of the relative values, the
data classified can be
ranked or ordered.

31. Interval-Level Data
Properties:
1.Data classifications are ordered according to the amount of the
characteristic they possess.
2.Equal differences in the characteristic are represented by equal
differences in the measurements.
Example: Women’s dress sizes listed
on the table.

32. Ratio-Level Data
• Practically all quantitative data is recorded on the ratio
level of measurement.
• Ratio level is the “highest” level of measurement.
Properties:
1.Data classifications are ordered according to the amount of the
characteristics they possess.
2.Equal differences in the characteristic are represented by equal
differences in the numbers assigned to the classifications.
3.The zero point is the absence of the characteristic and the ratio
between two numbers is meaningful.

33. Why Know the Level of Measurement of a Data?
• The level of measurement of the data dictates the
calculations that can be done to summarize and
present the data.
• To determine the statistical tests that should be
performed on the data

34. Summary of the Characteristics for Levels of
Measurement