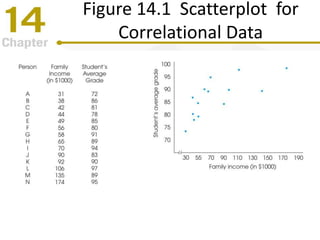
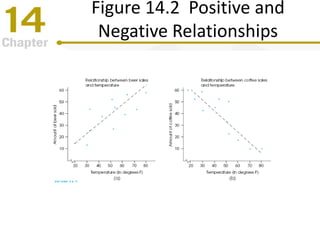
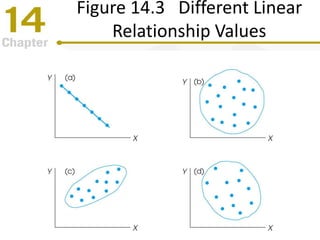
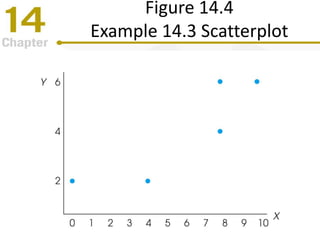
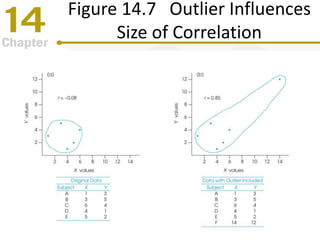
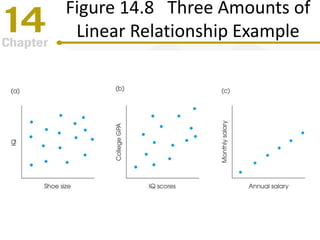
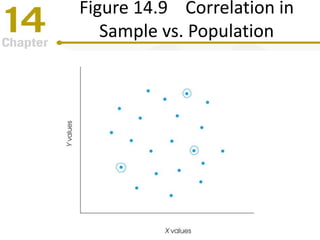
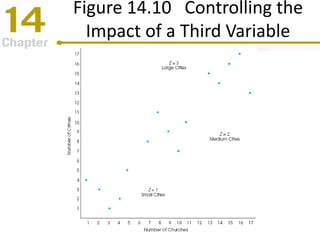
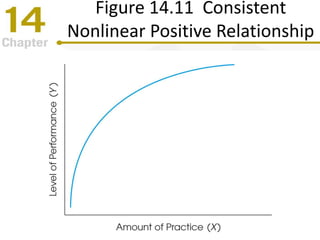
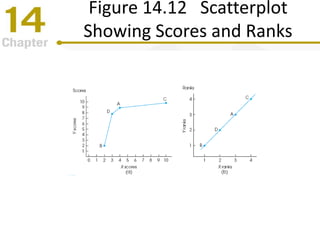
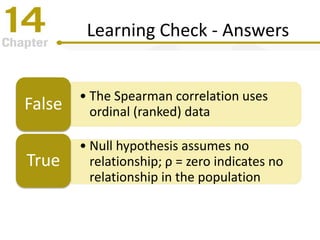
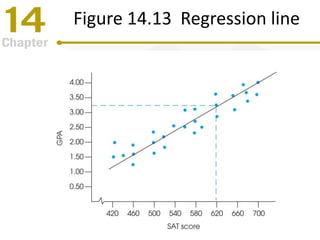
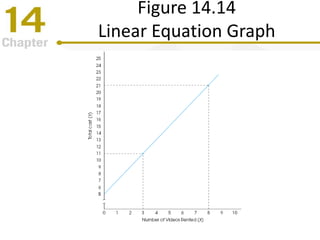
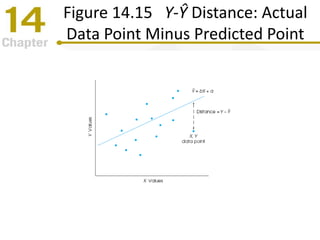
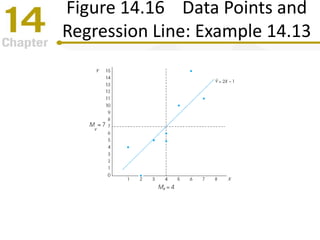
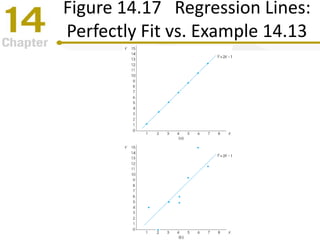
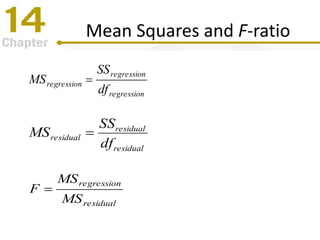
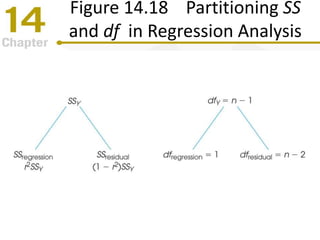
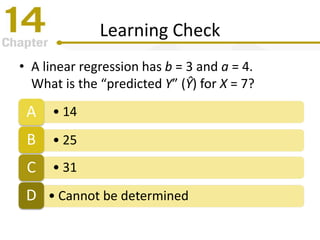
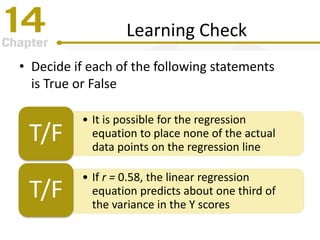
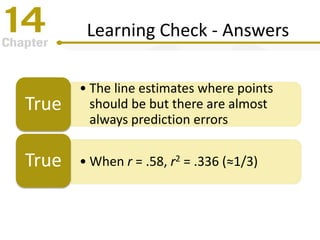
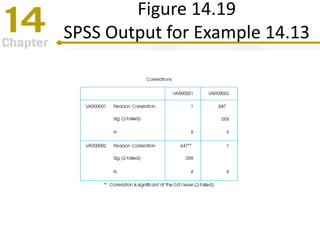
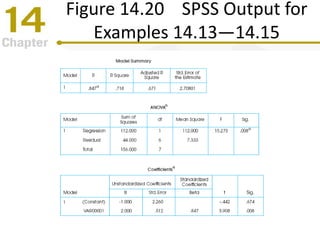
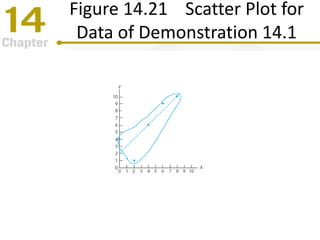
Chapter 14 focuses on correlation and regression in statistical analysis, covering Pearson correlation, its calculation, interpretation, and the conditions under which it is used. It discusses the significance of evaluating correlations and the difference between correlation and causation, along with alternative correlation methods like Spearman and point-biserial coefficients. The chapter also introduces linear regression, detailing the regression equation, error estimation, and significance testing methods.