Ken Plummer, profile picture
Uploaded byKen Plummer
PPTX, PDF8,950 views

Multiple linear regression

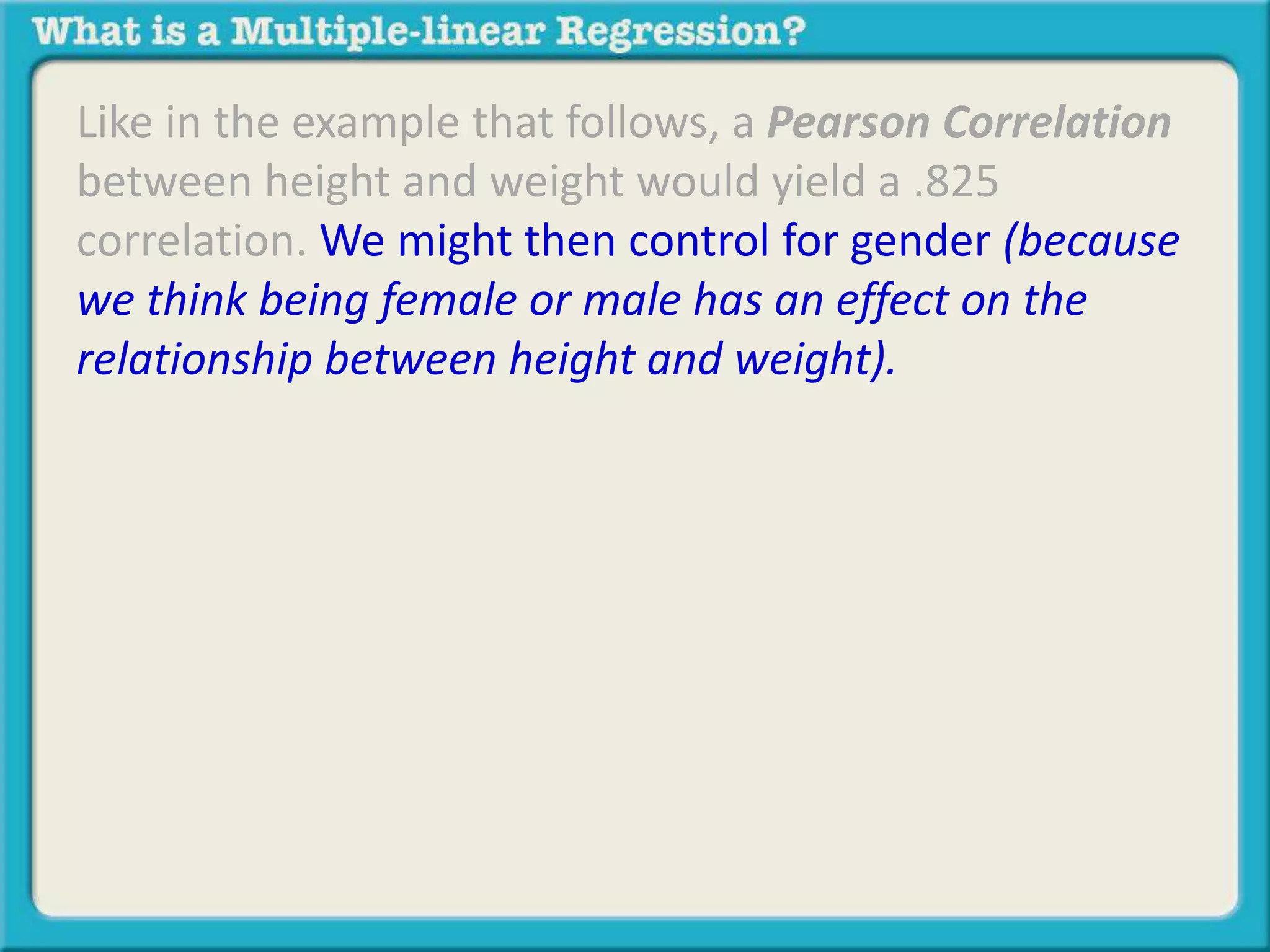
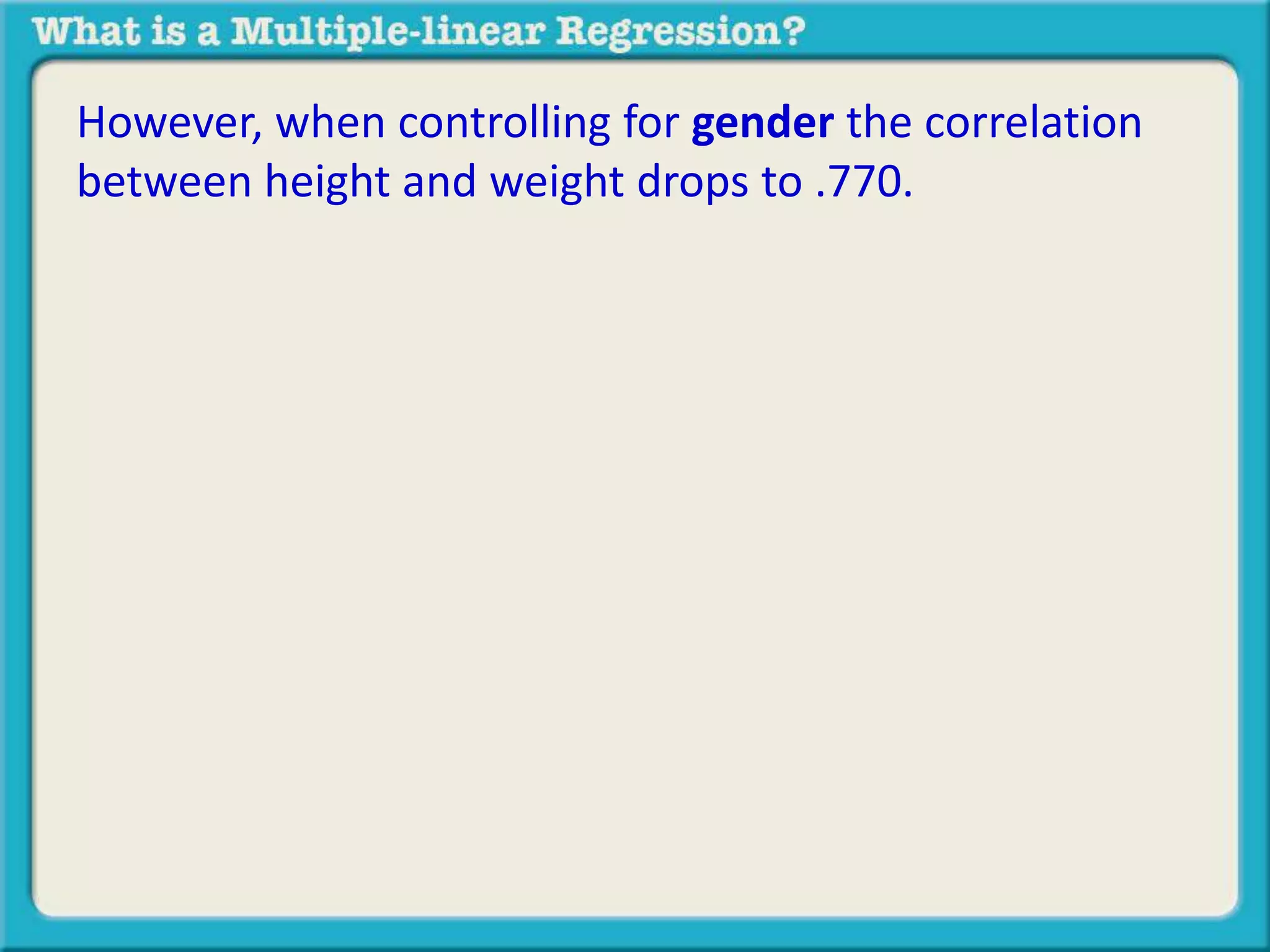
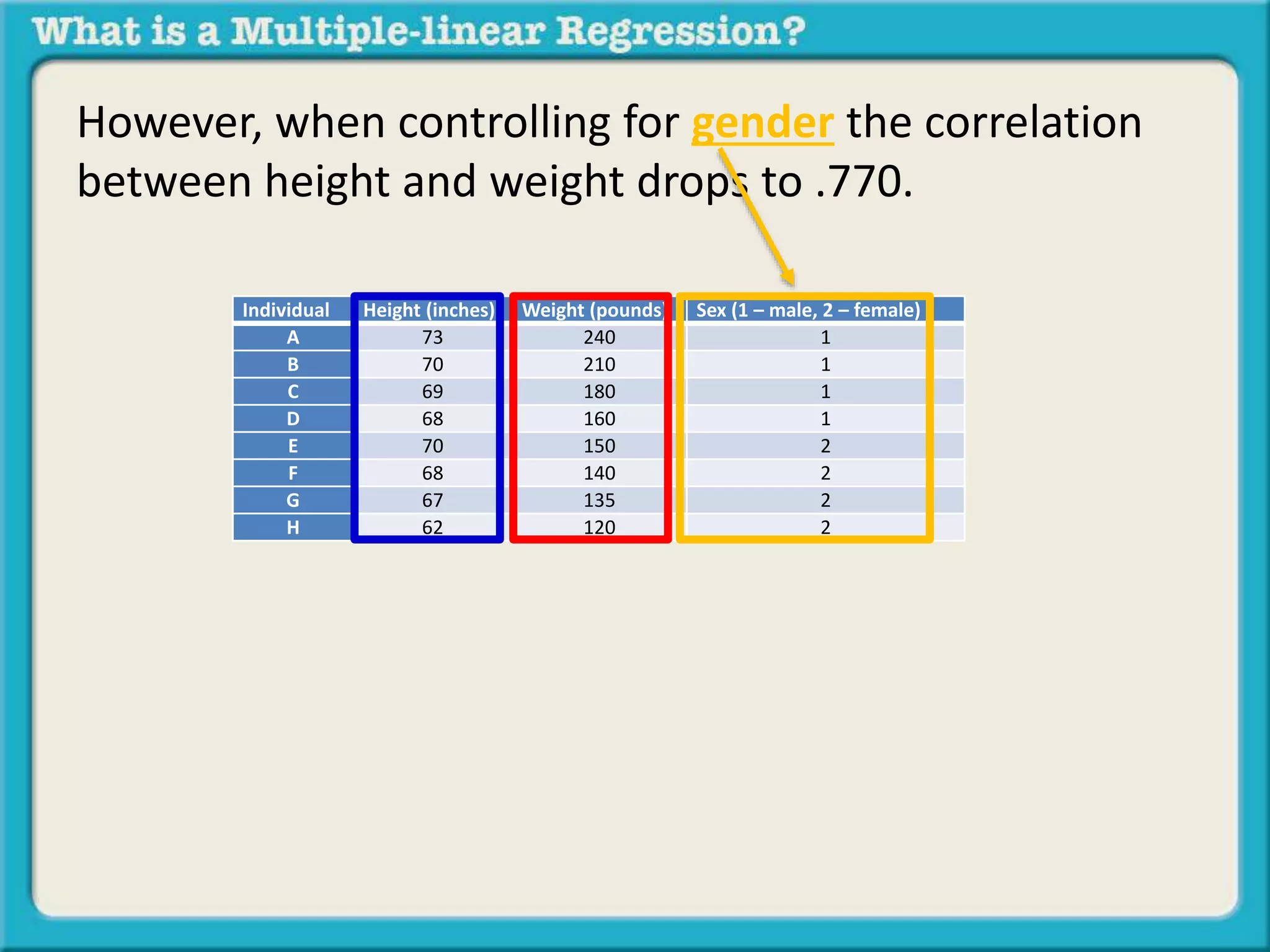
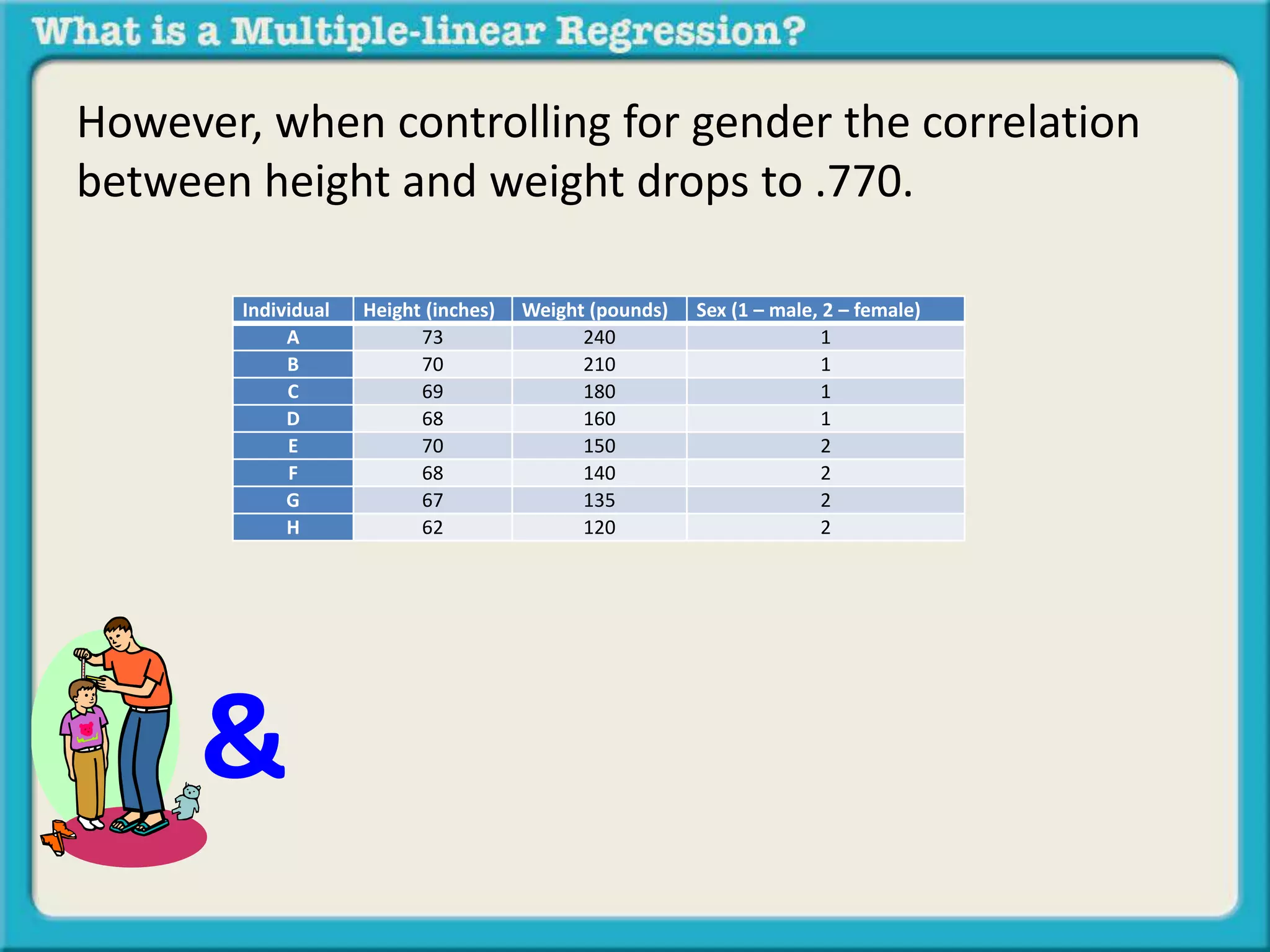
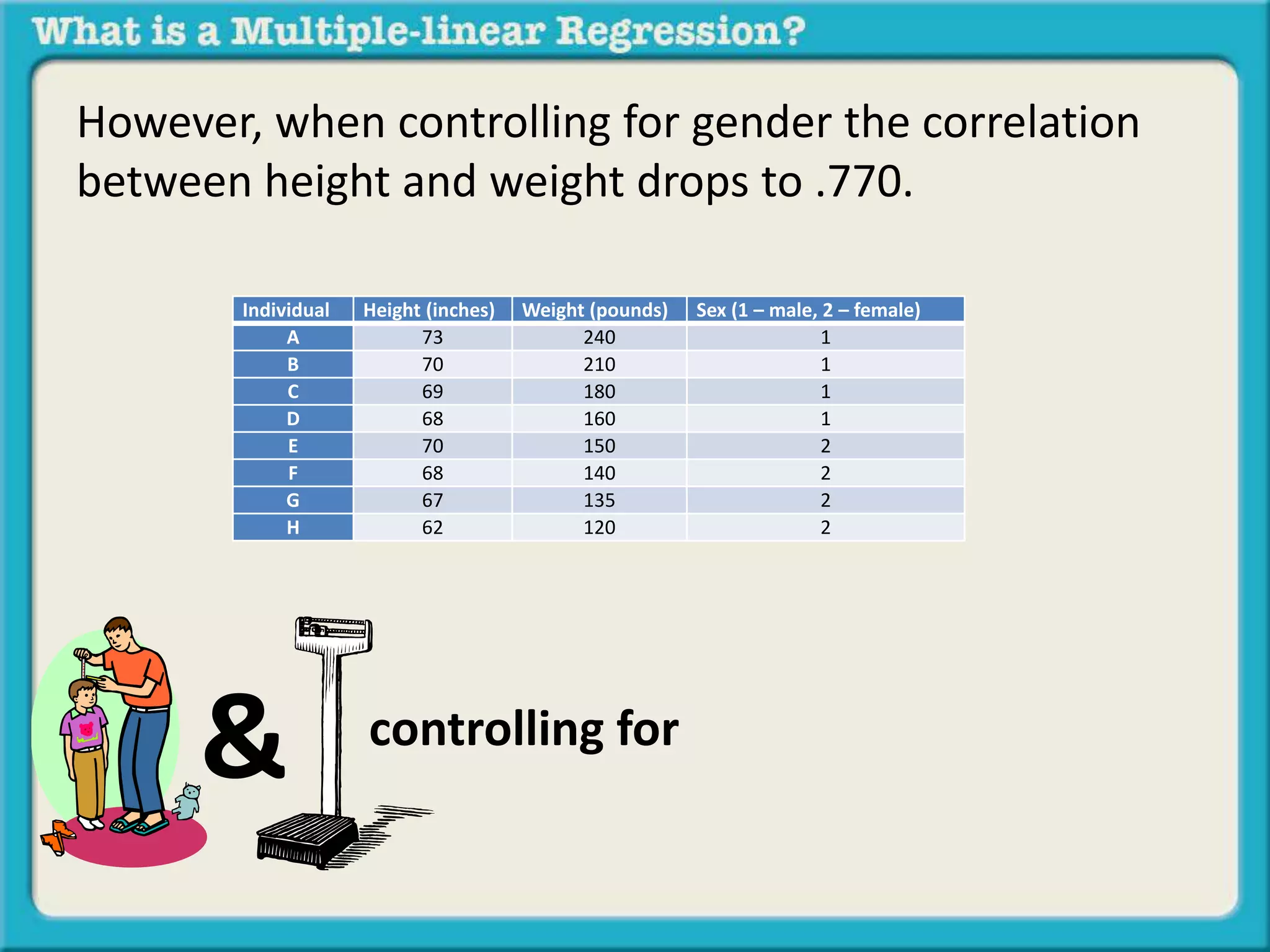
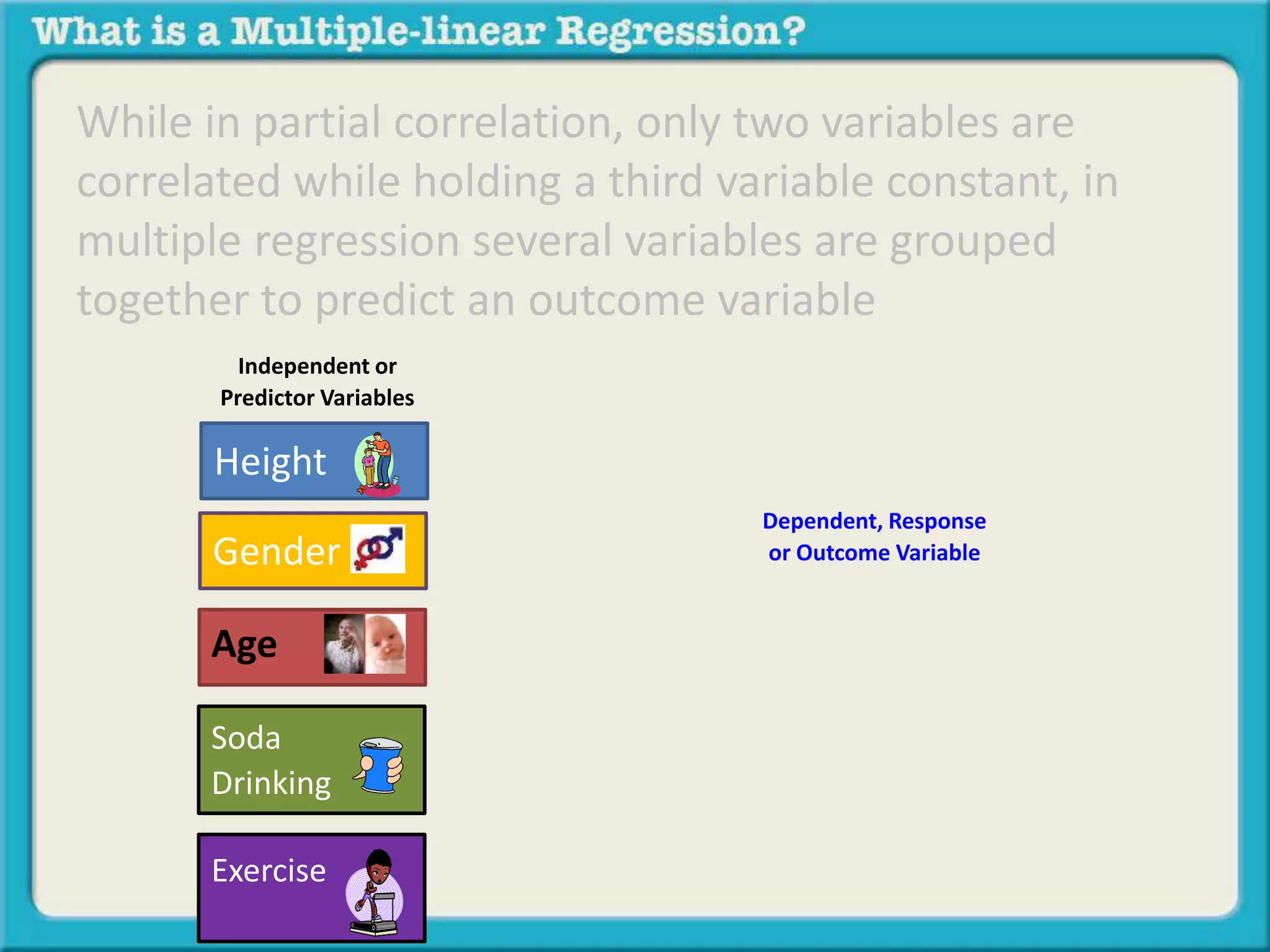
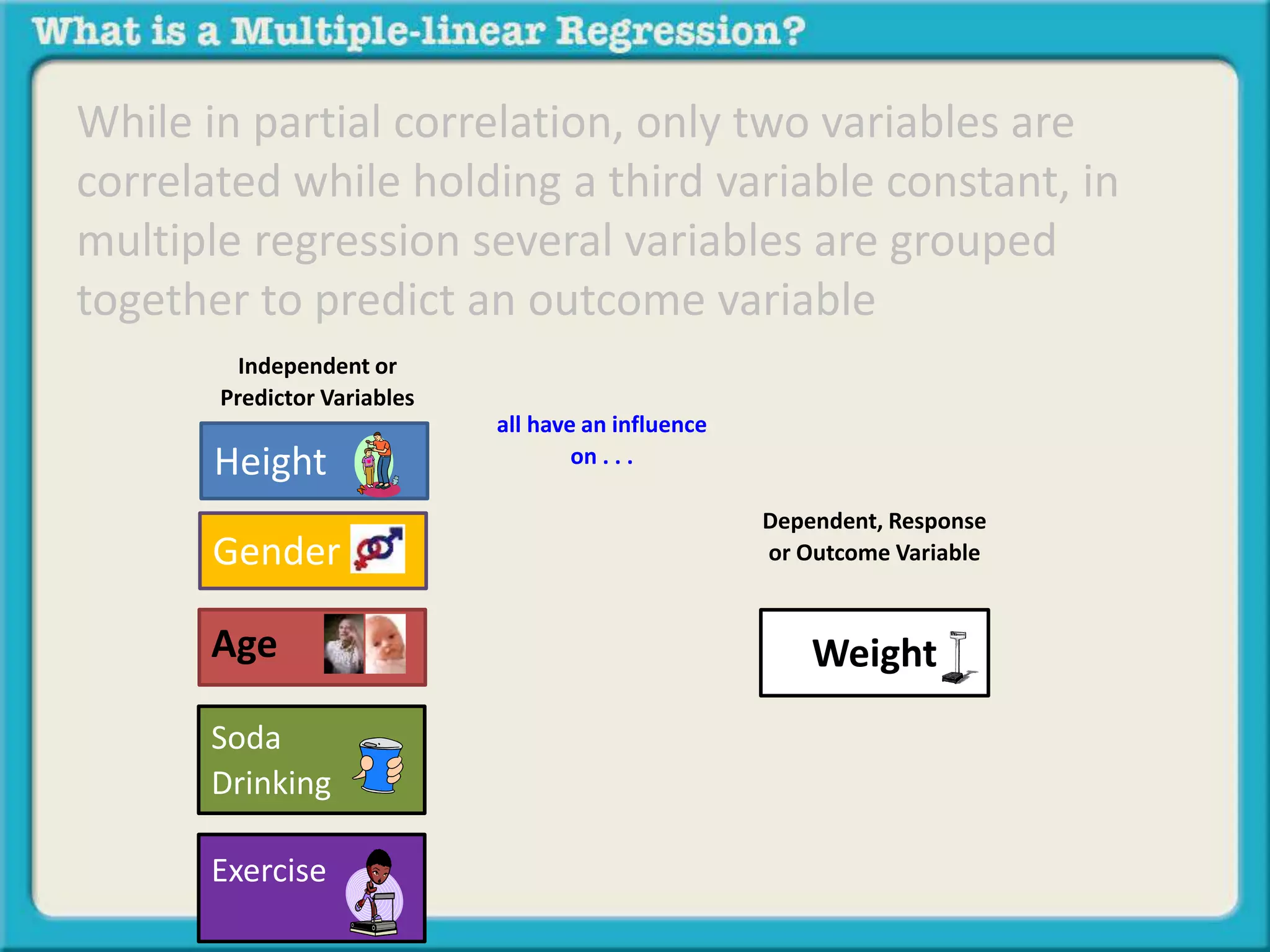
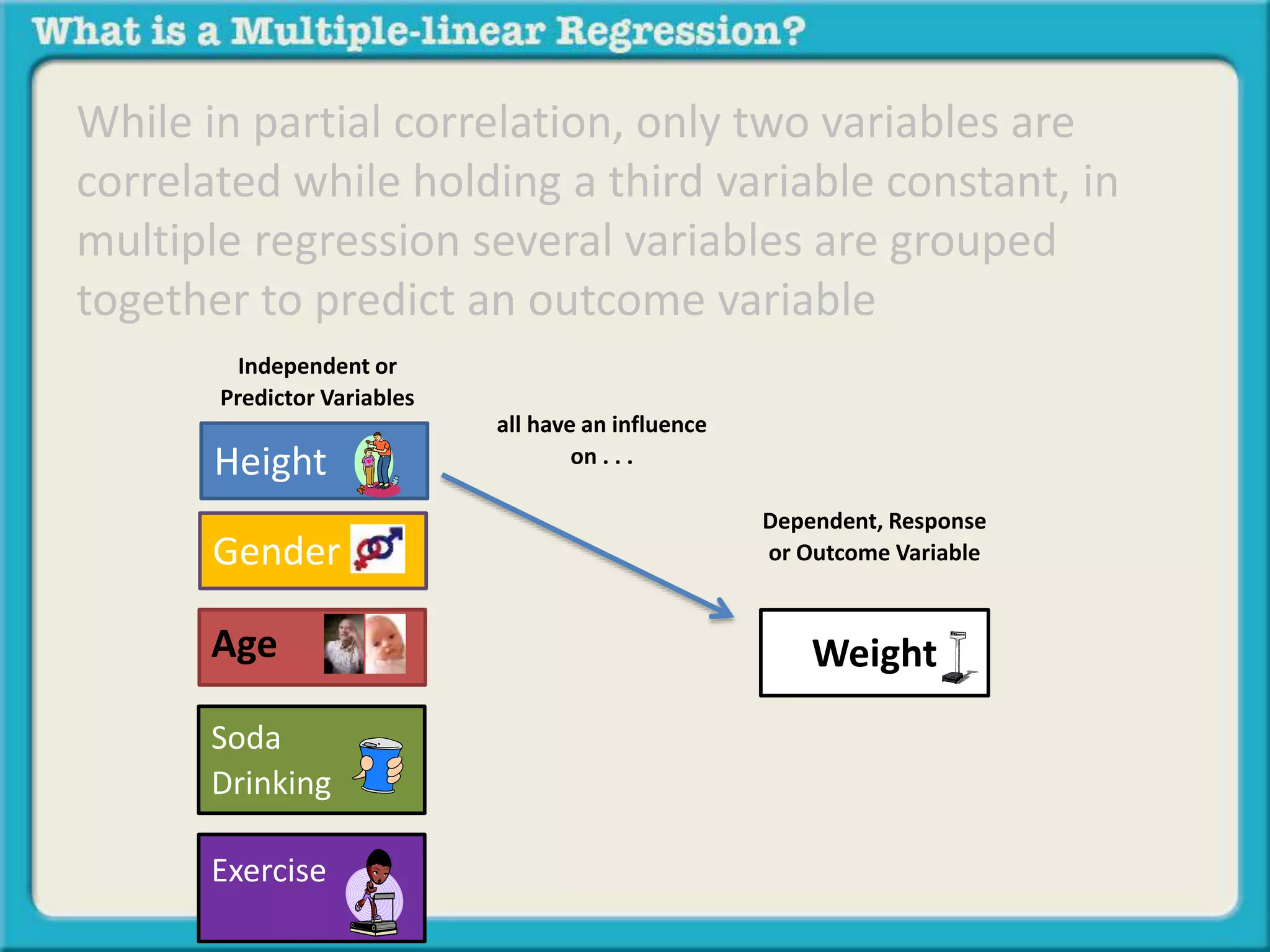
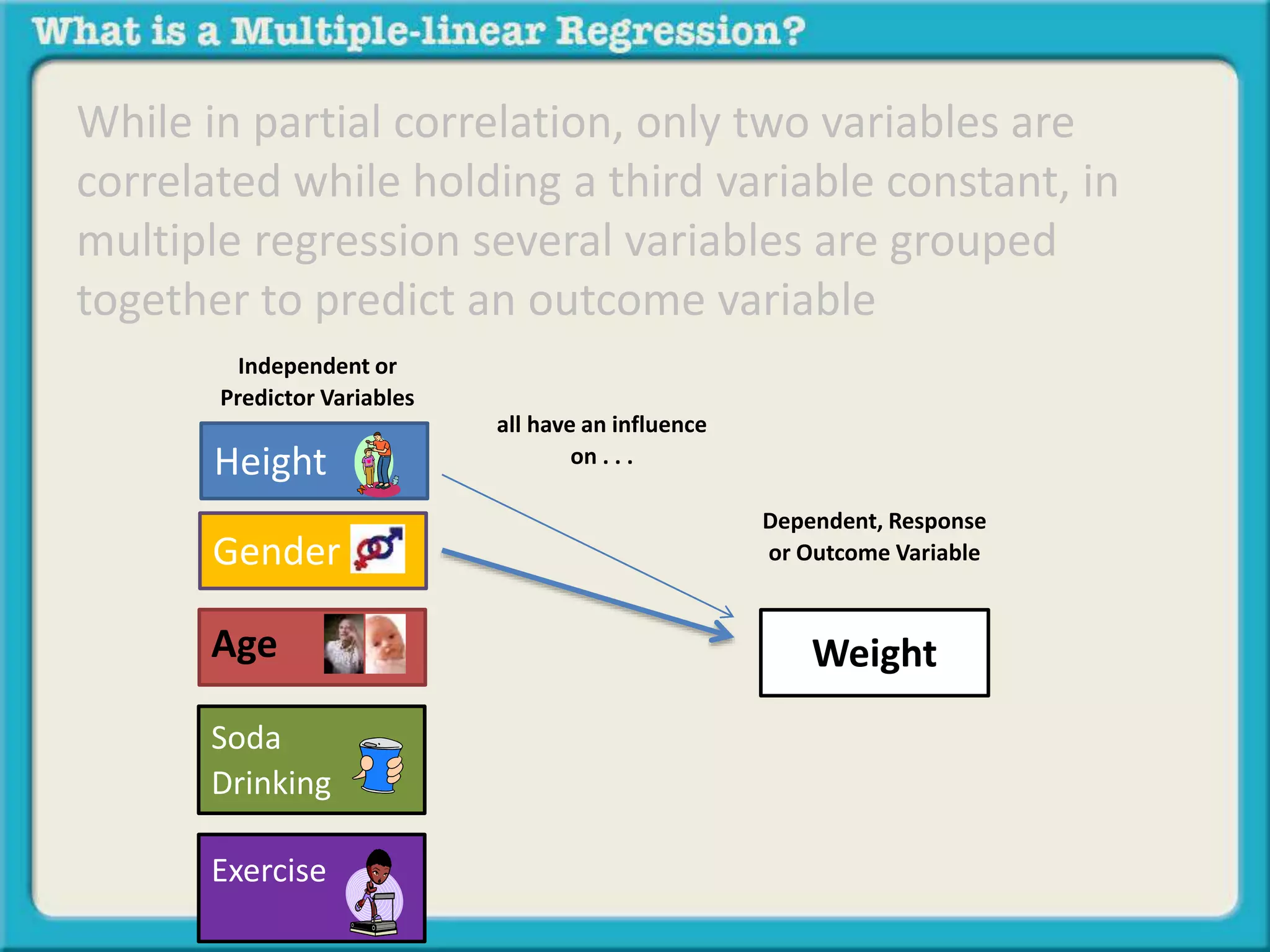
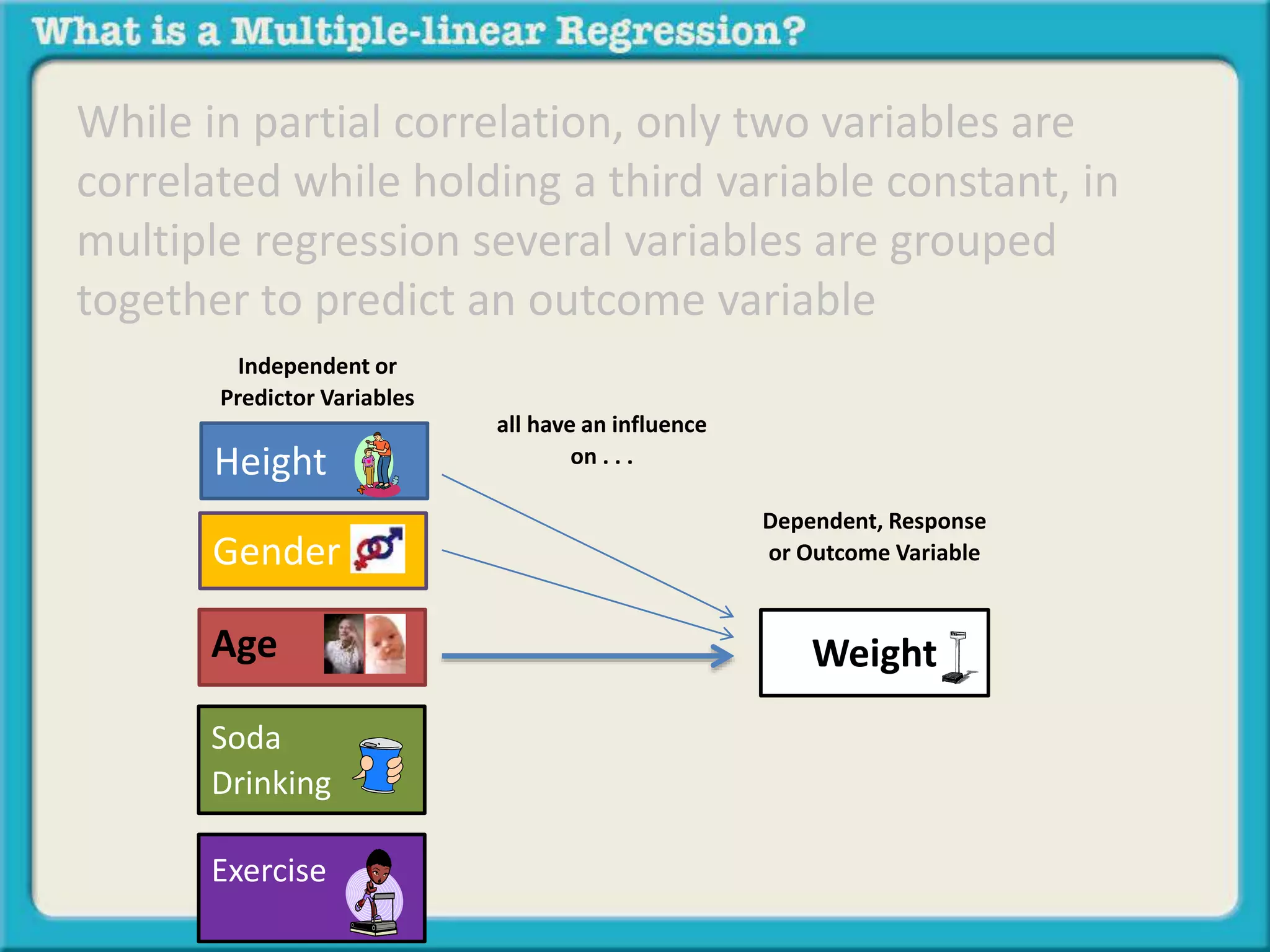
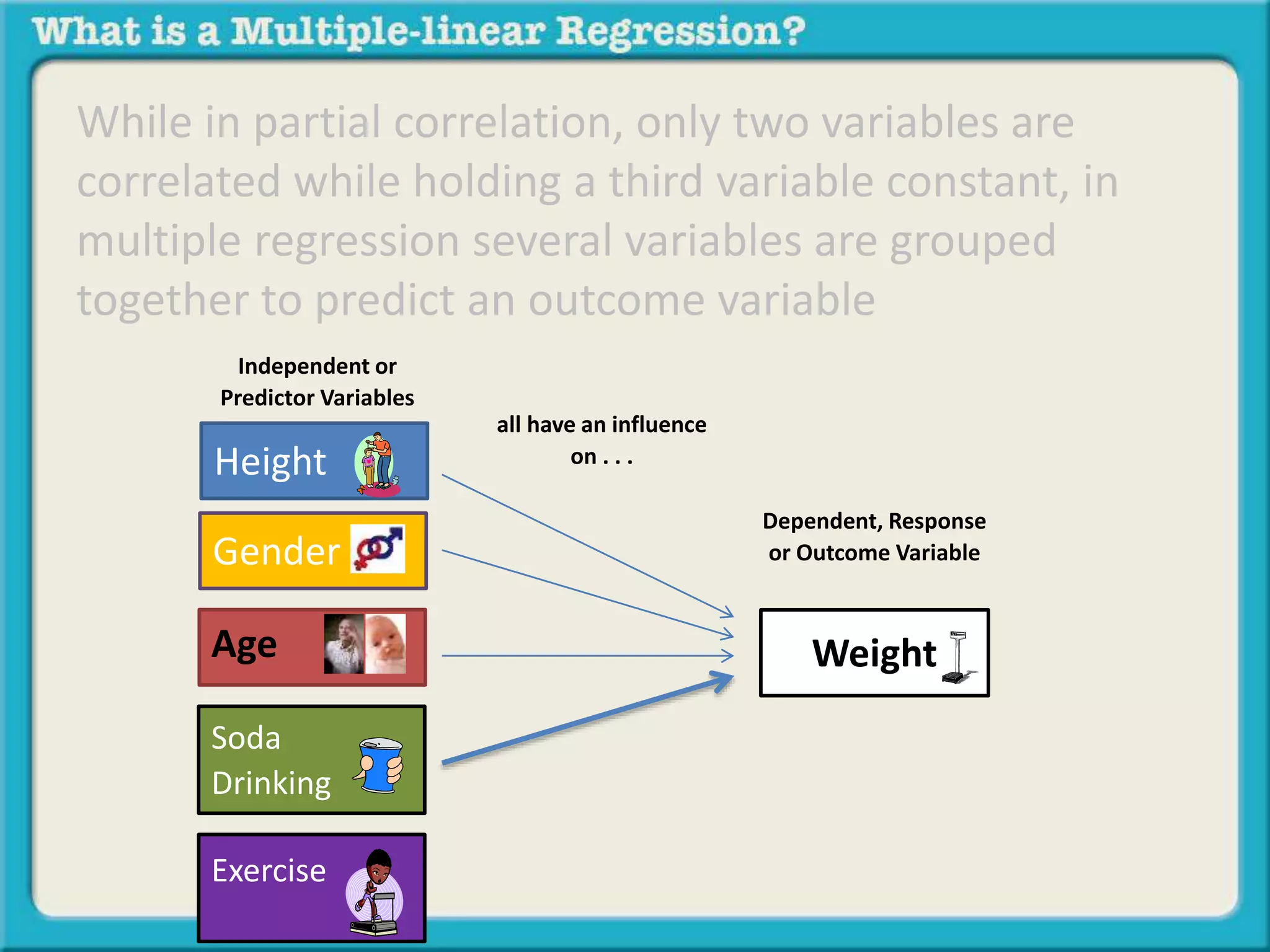
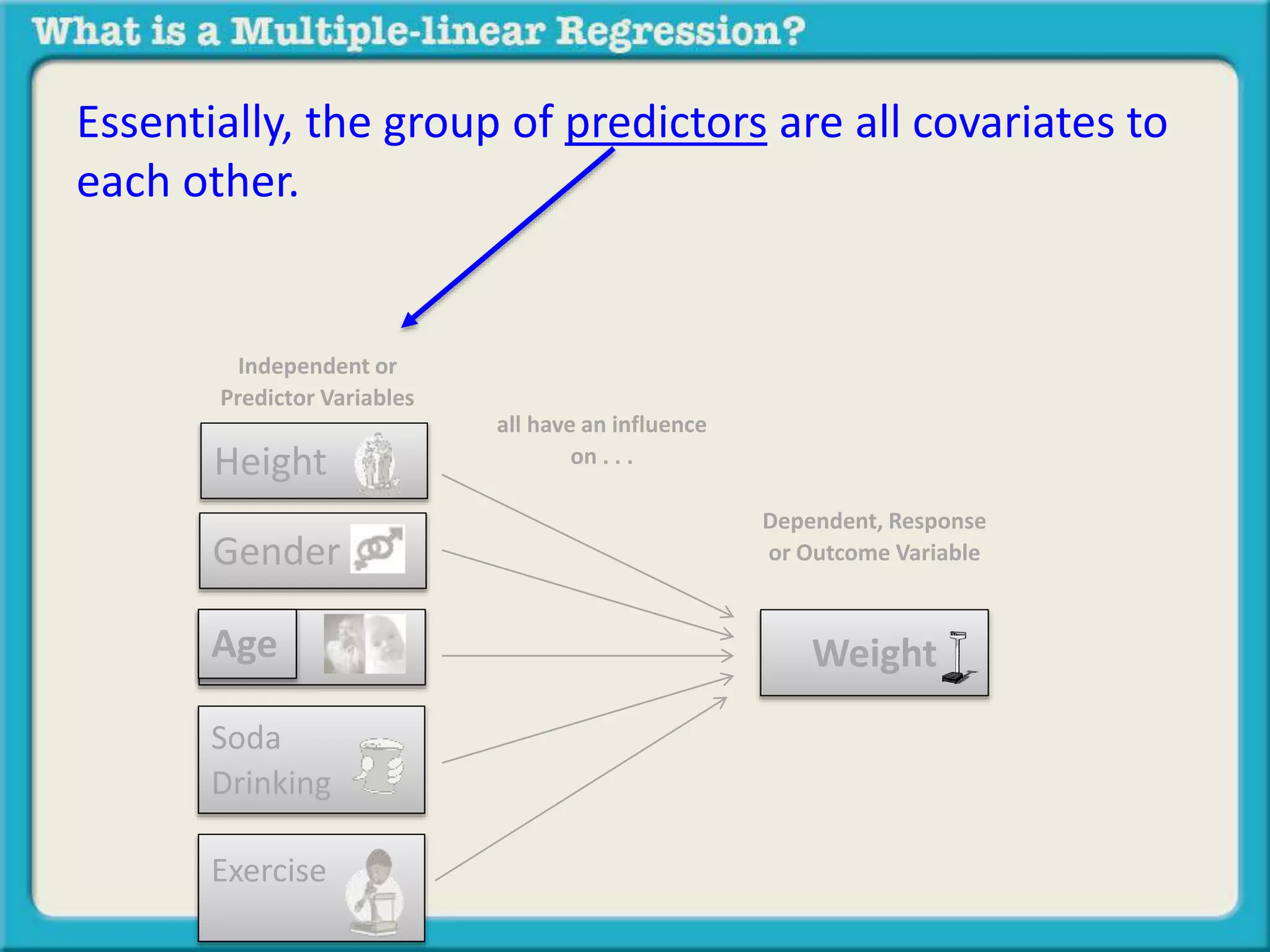
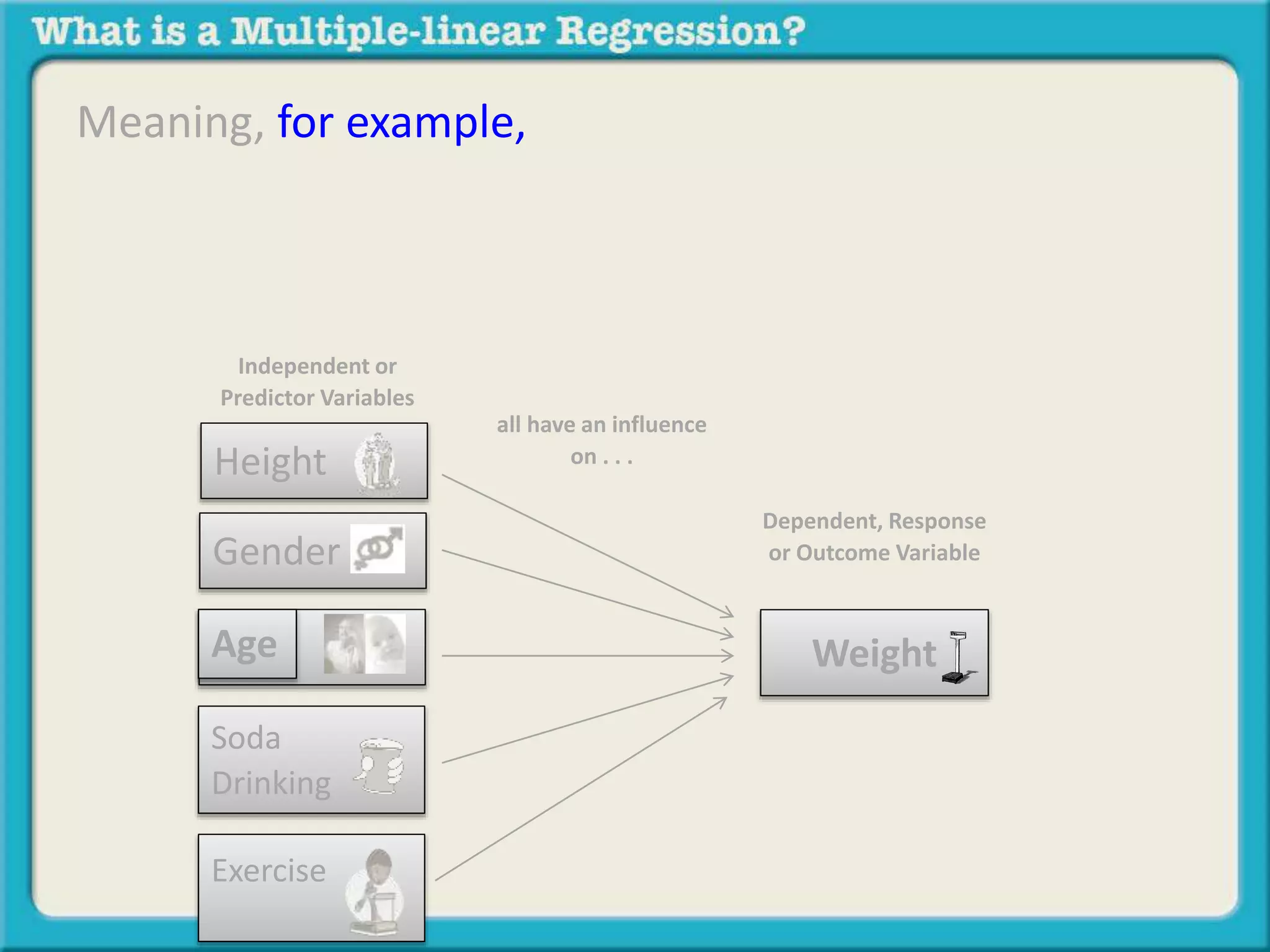
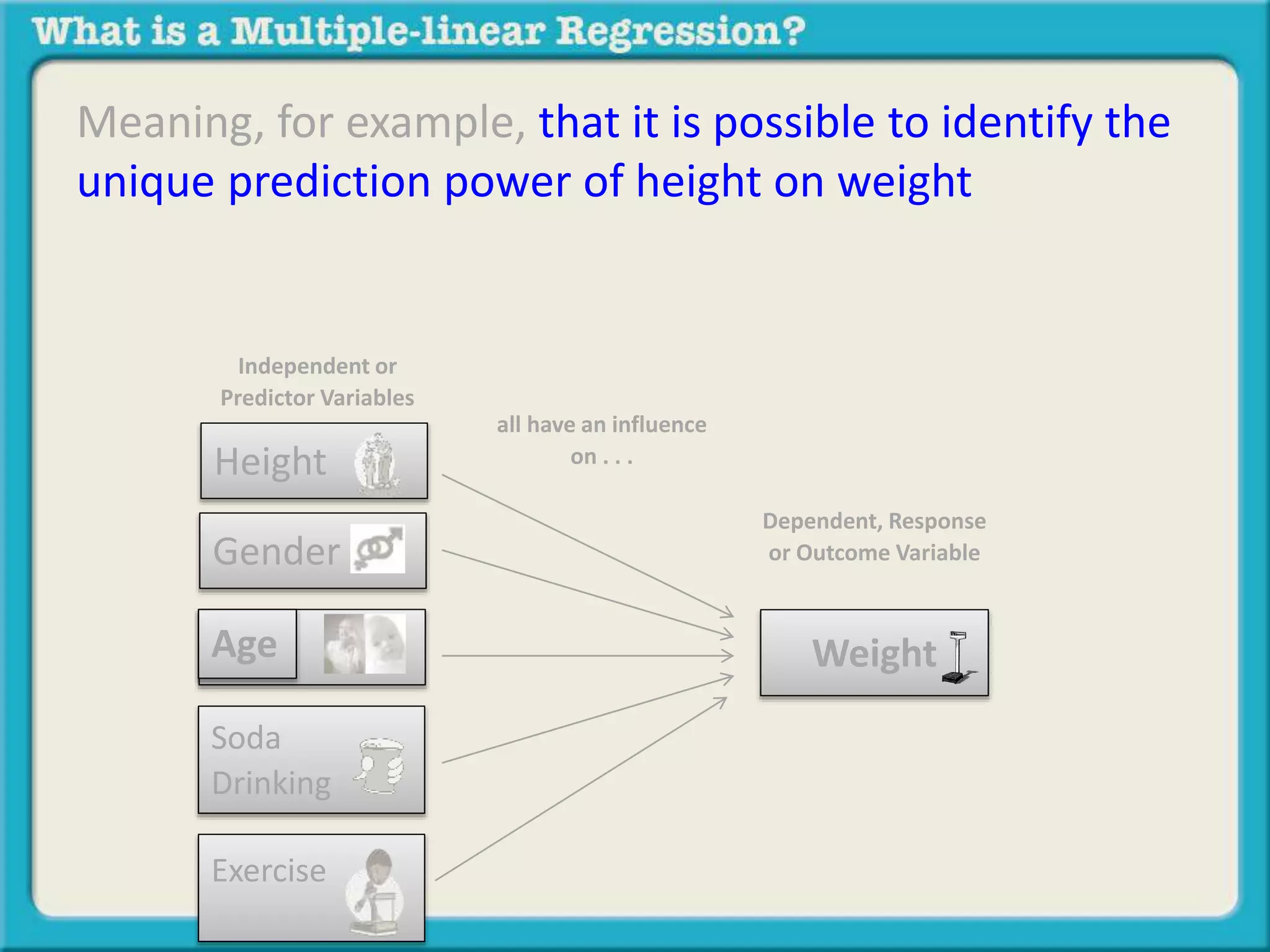
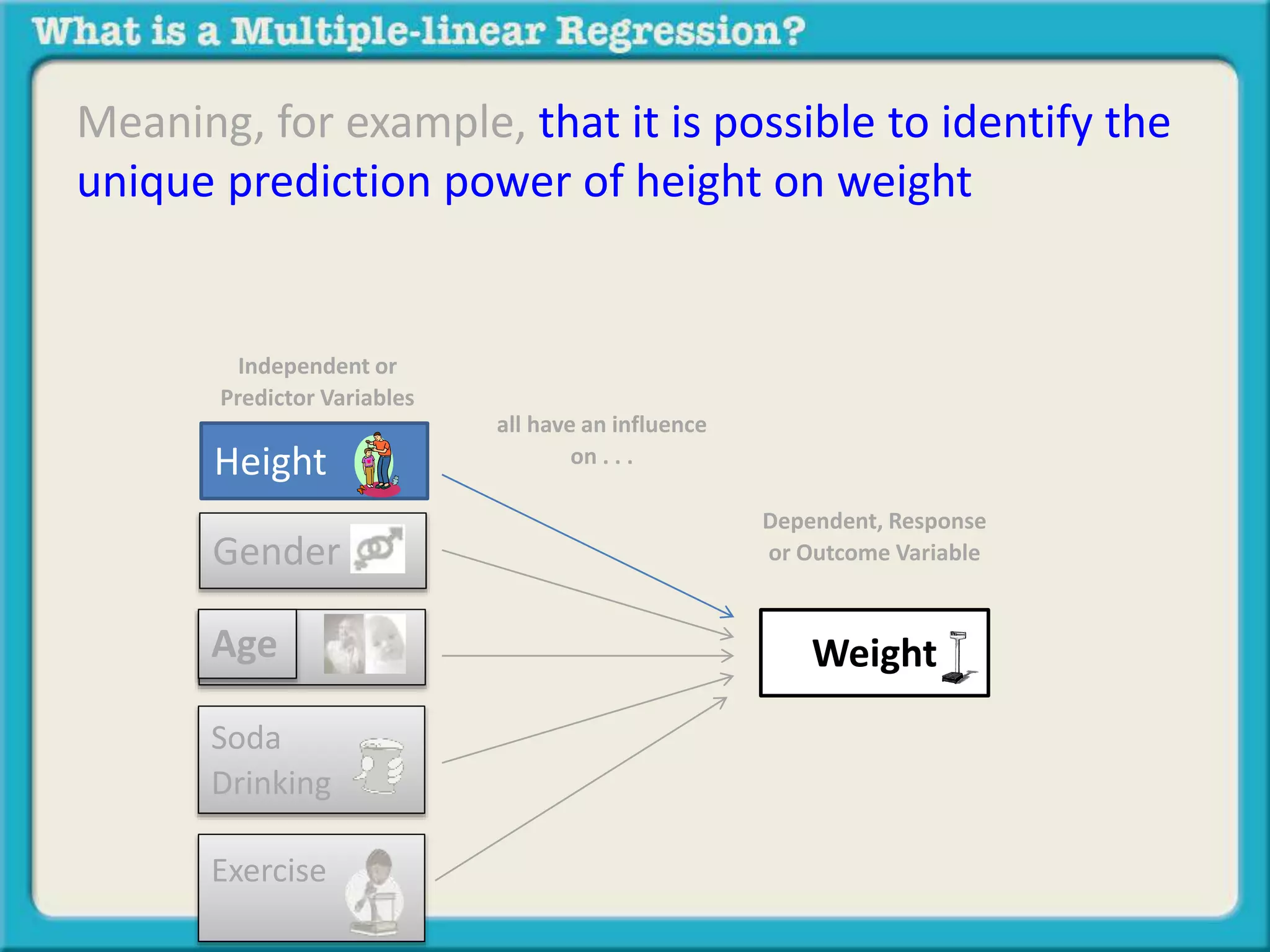
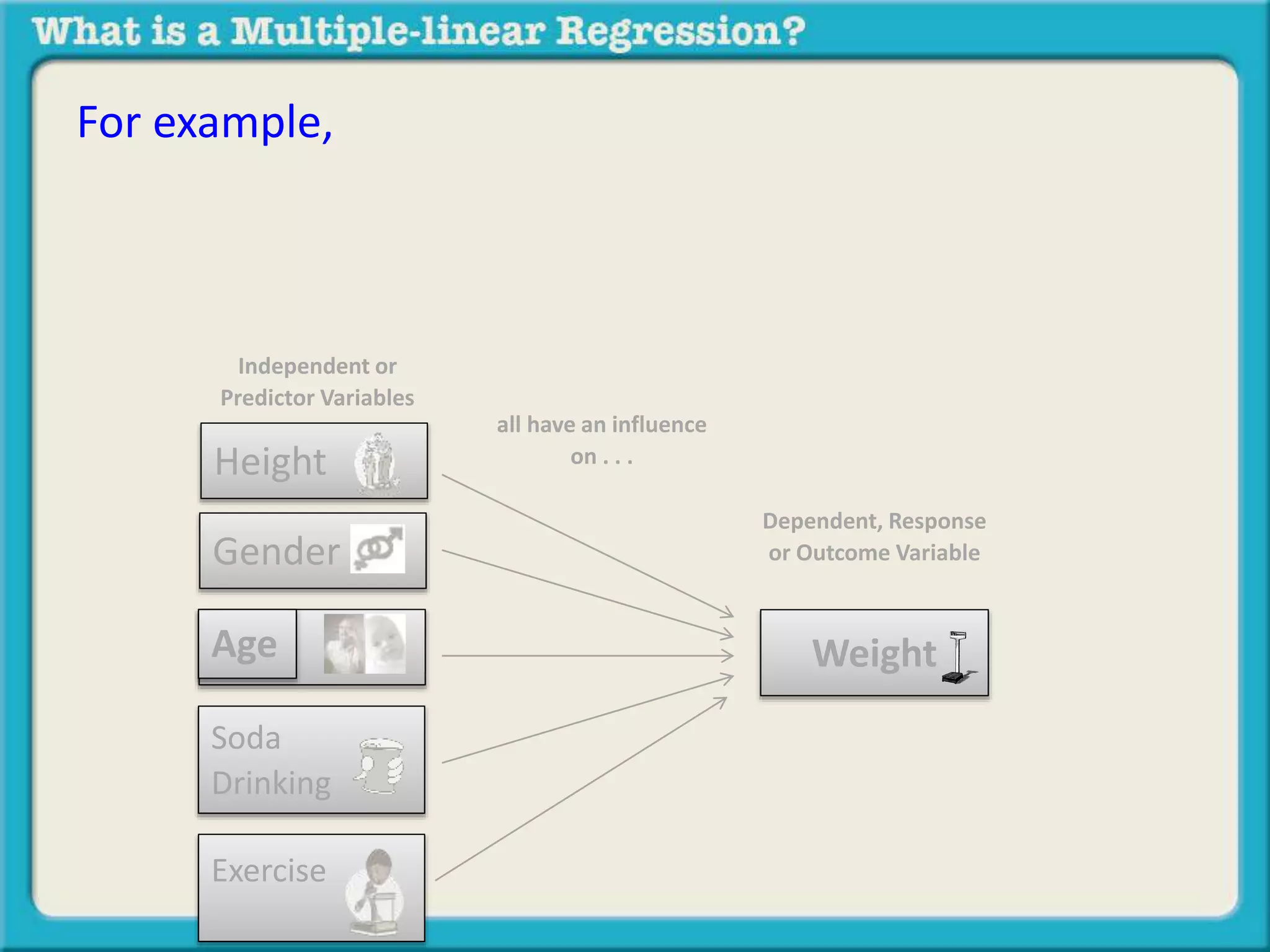
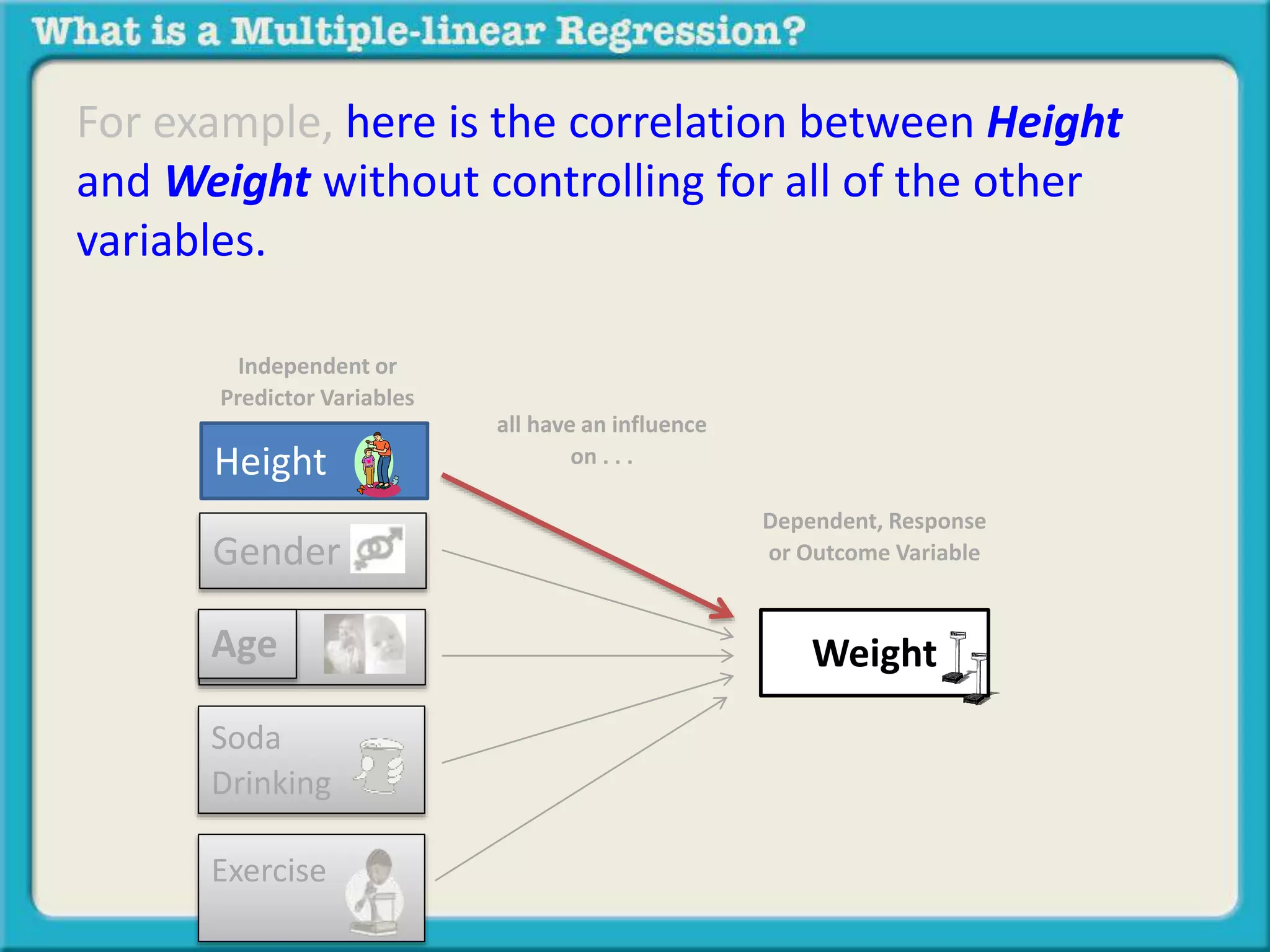
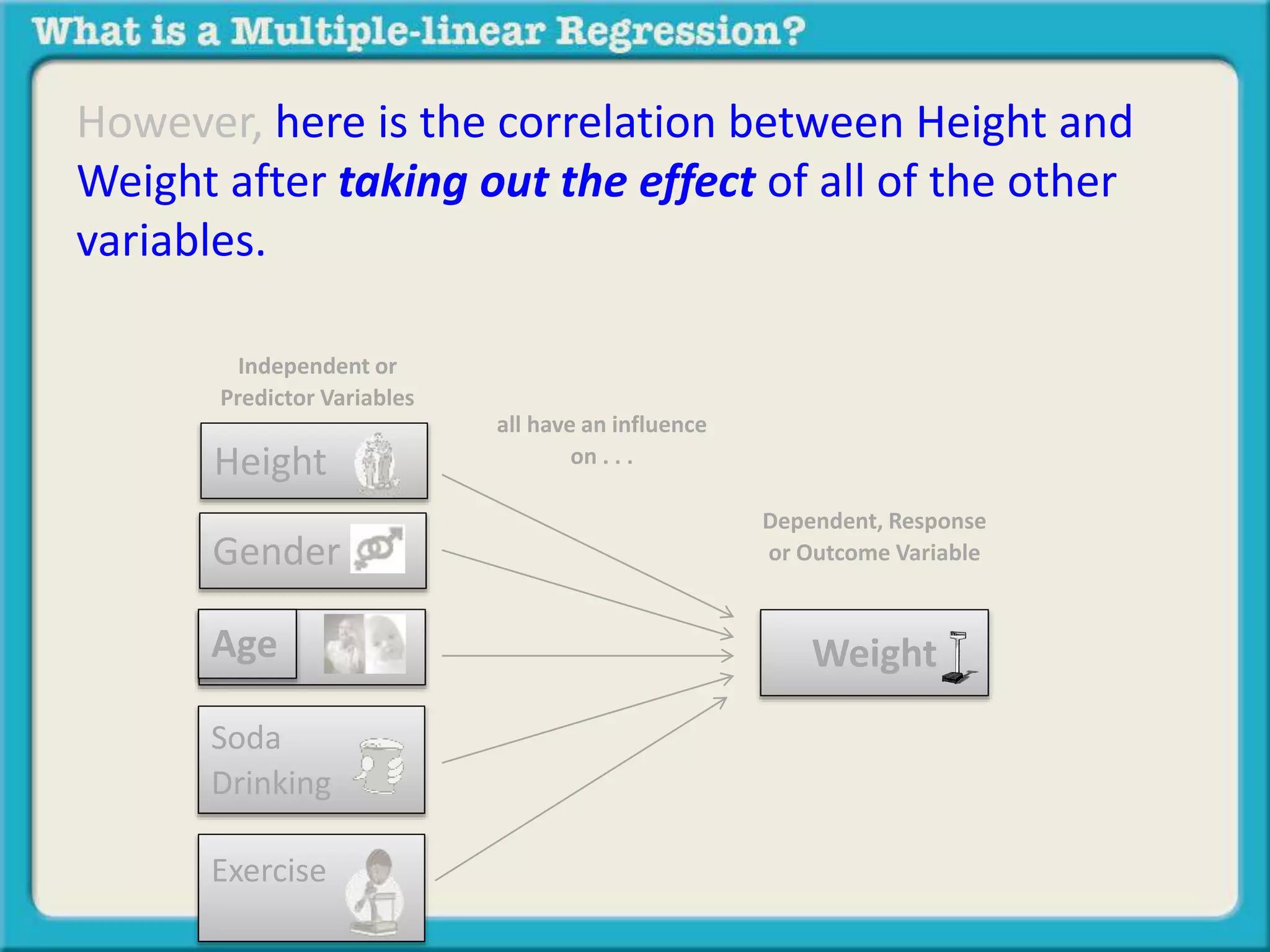
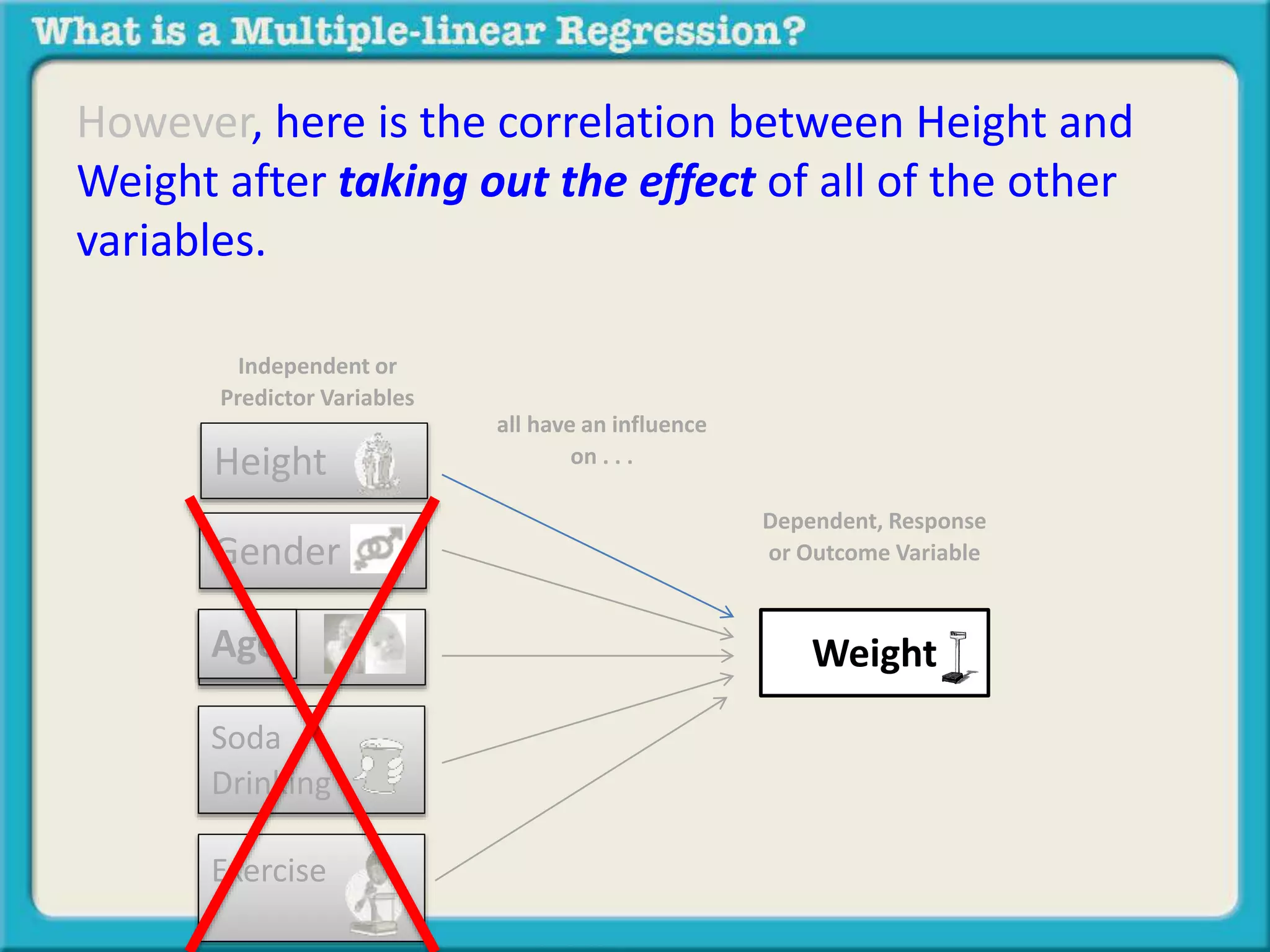
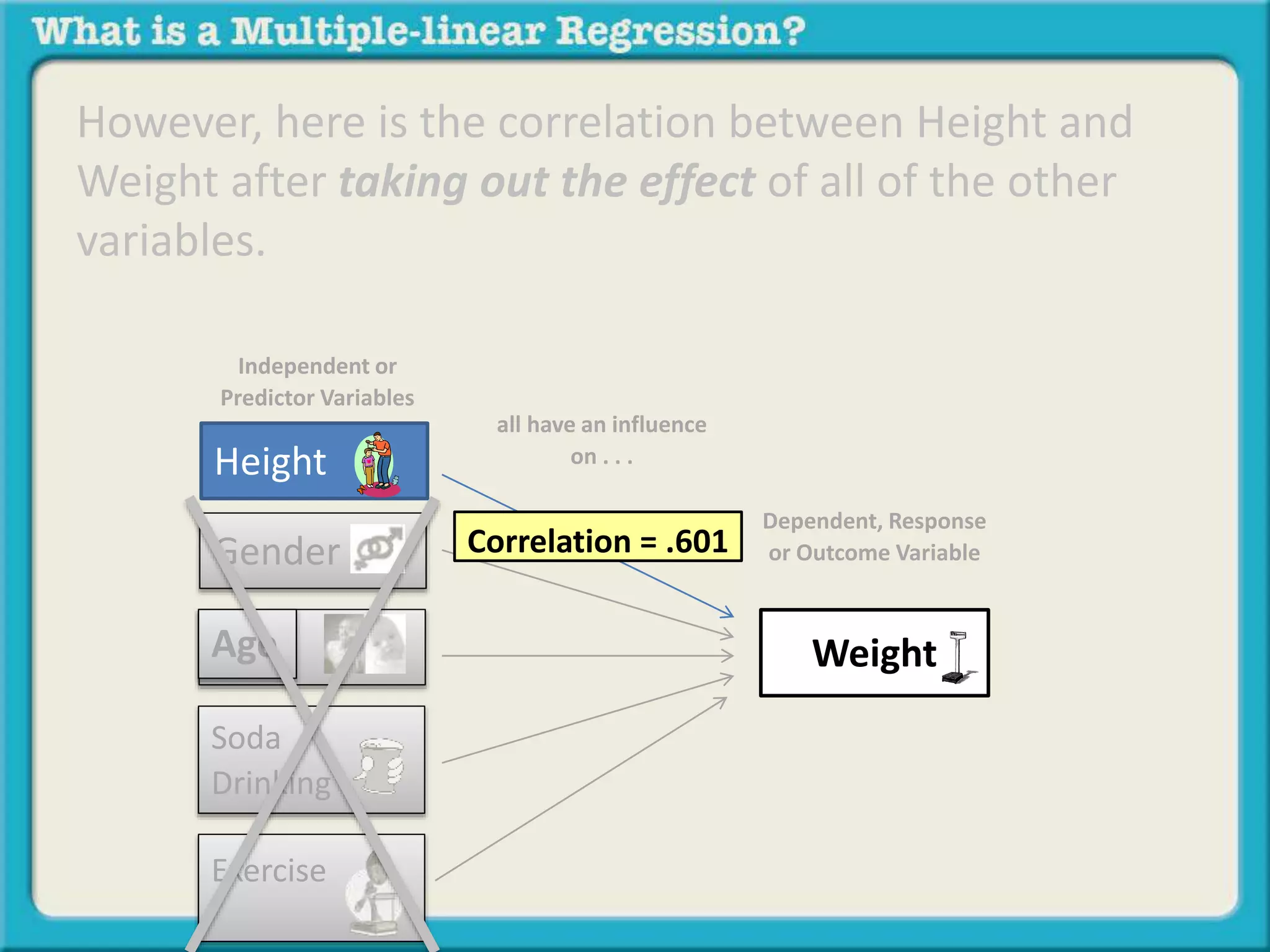
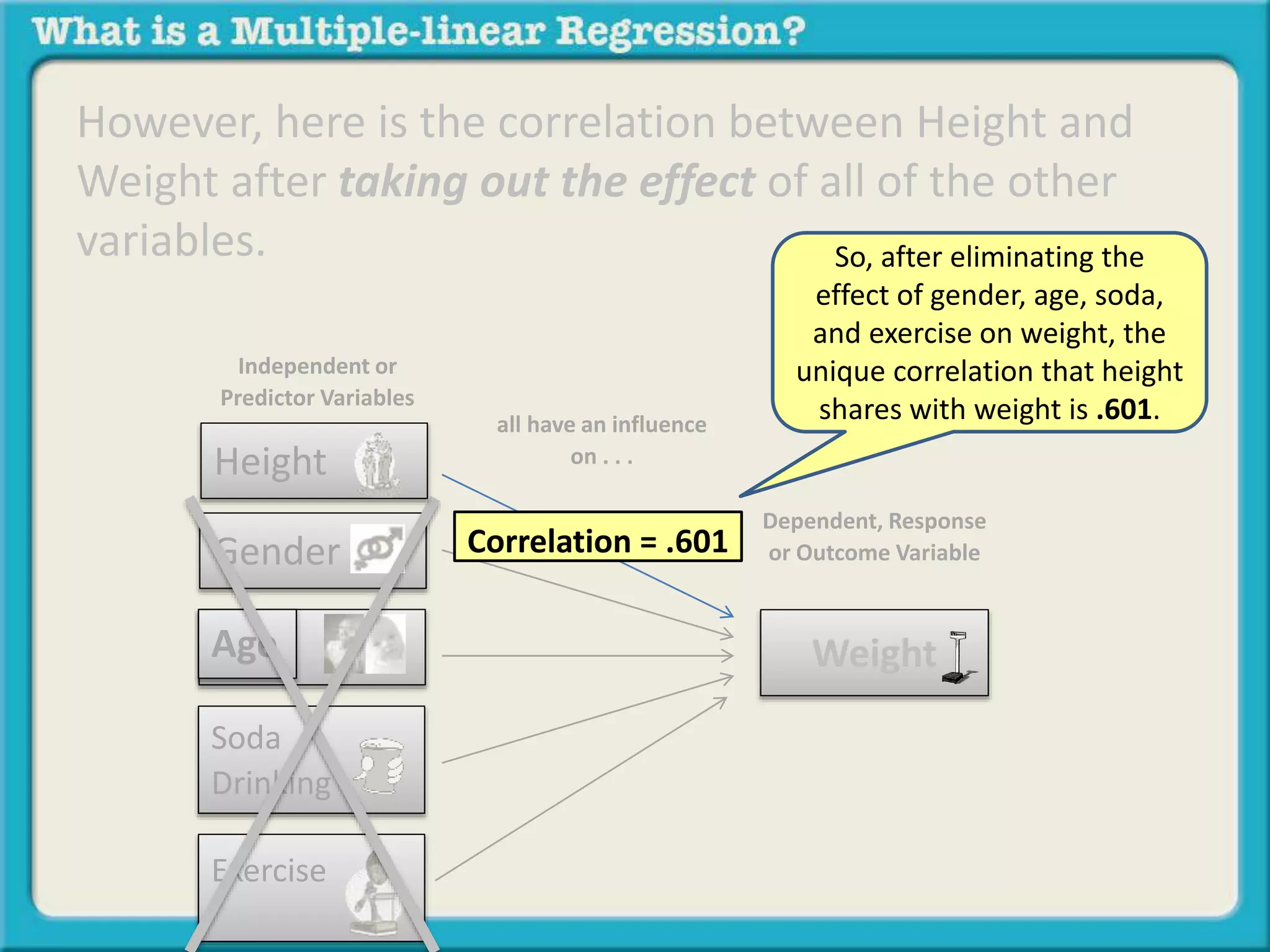
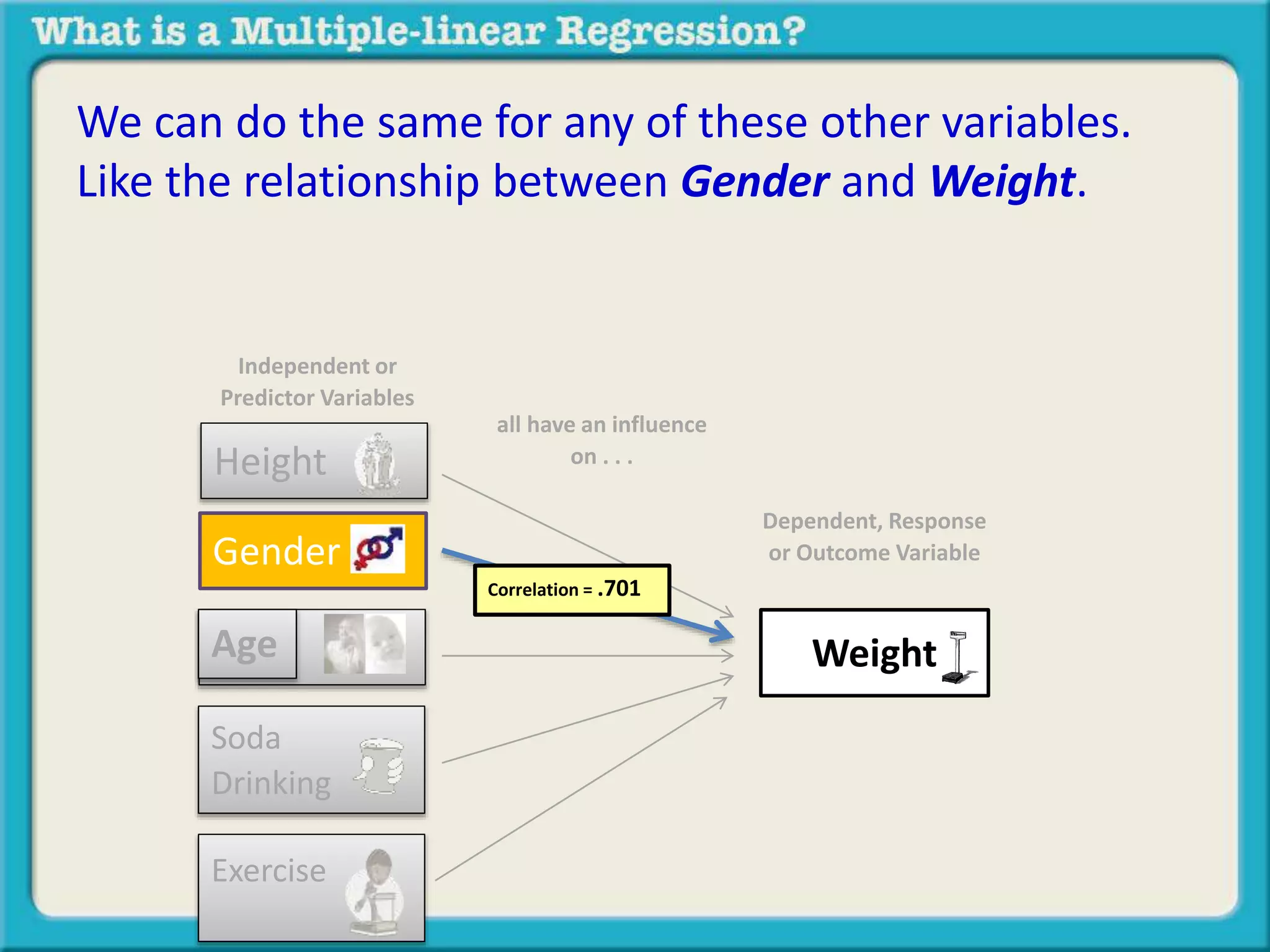
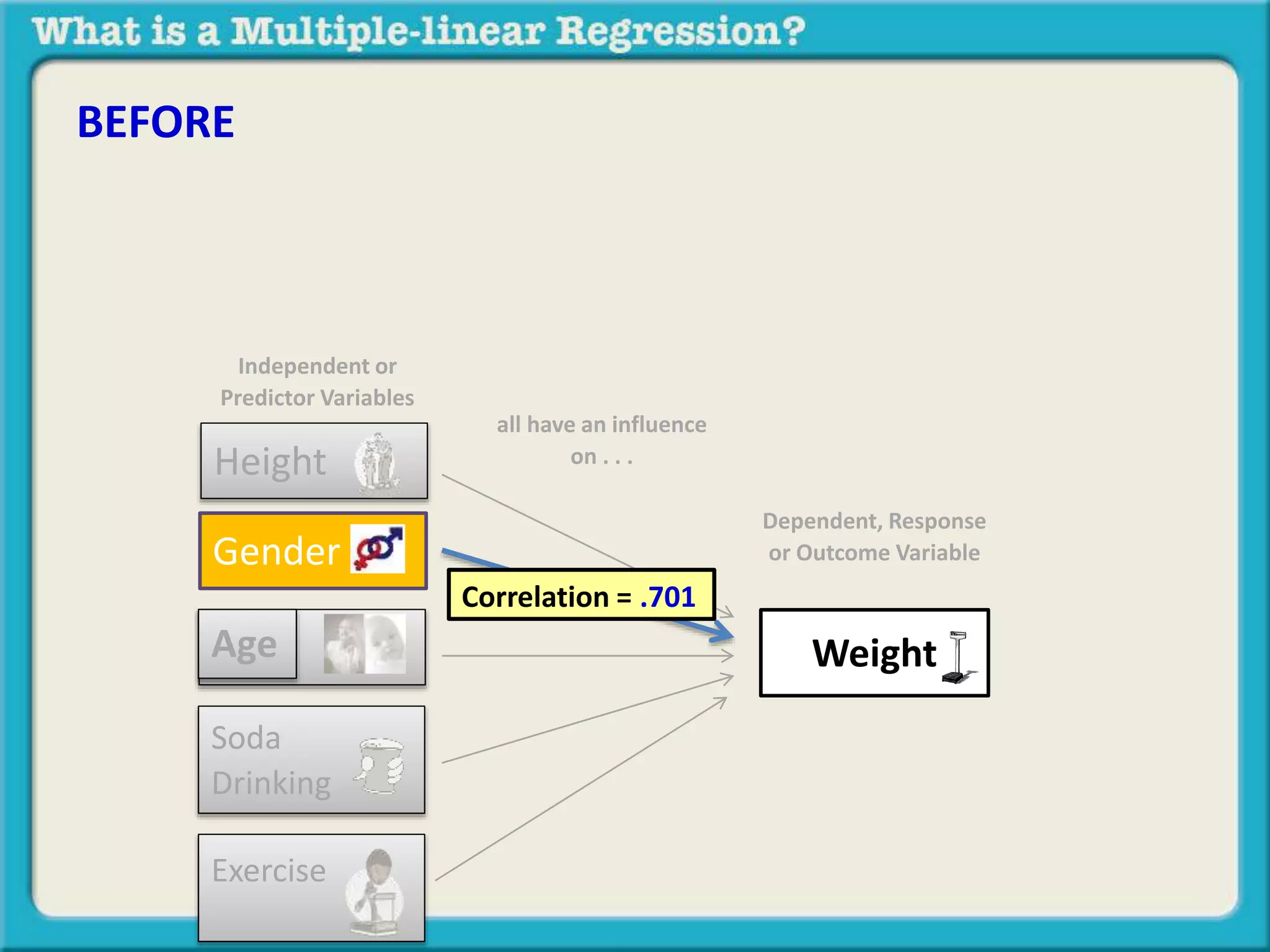
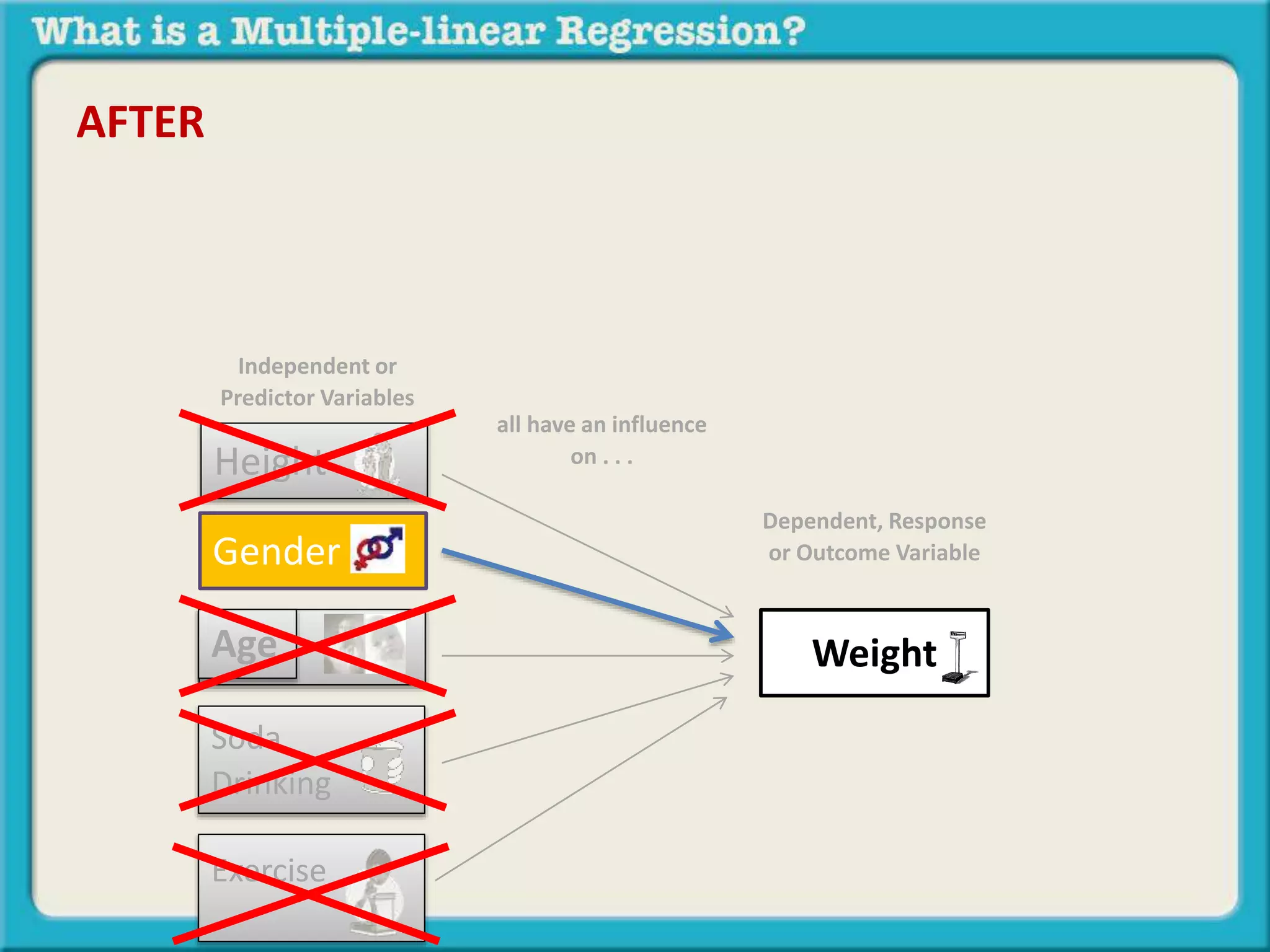
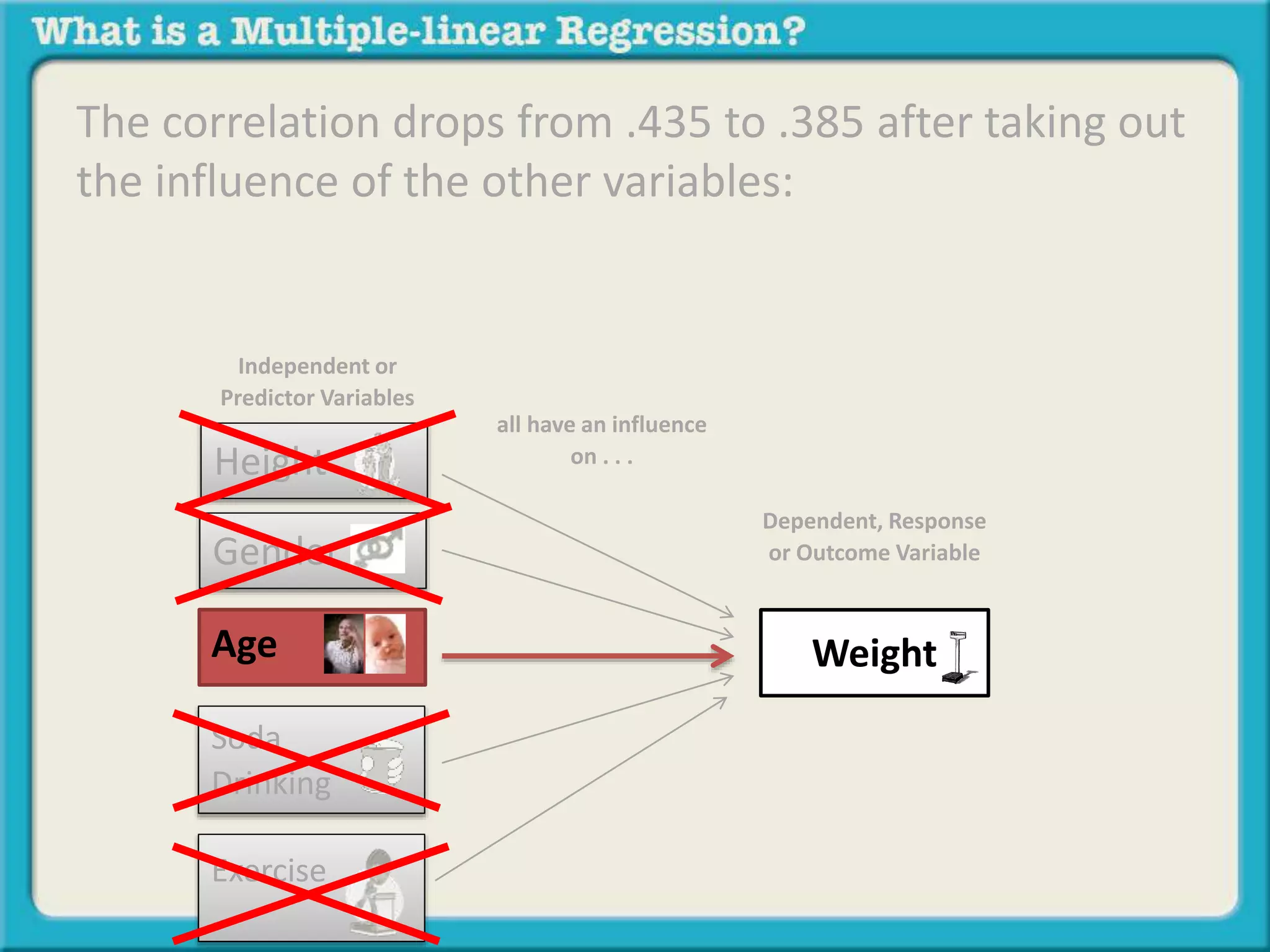
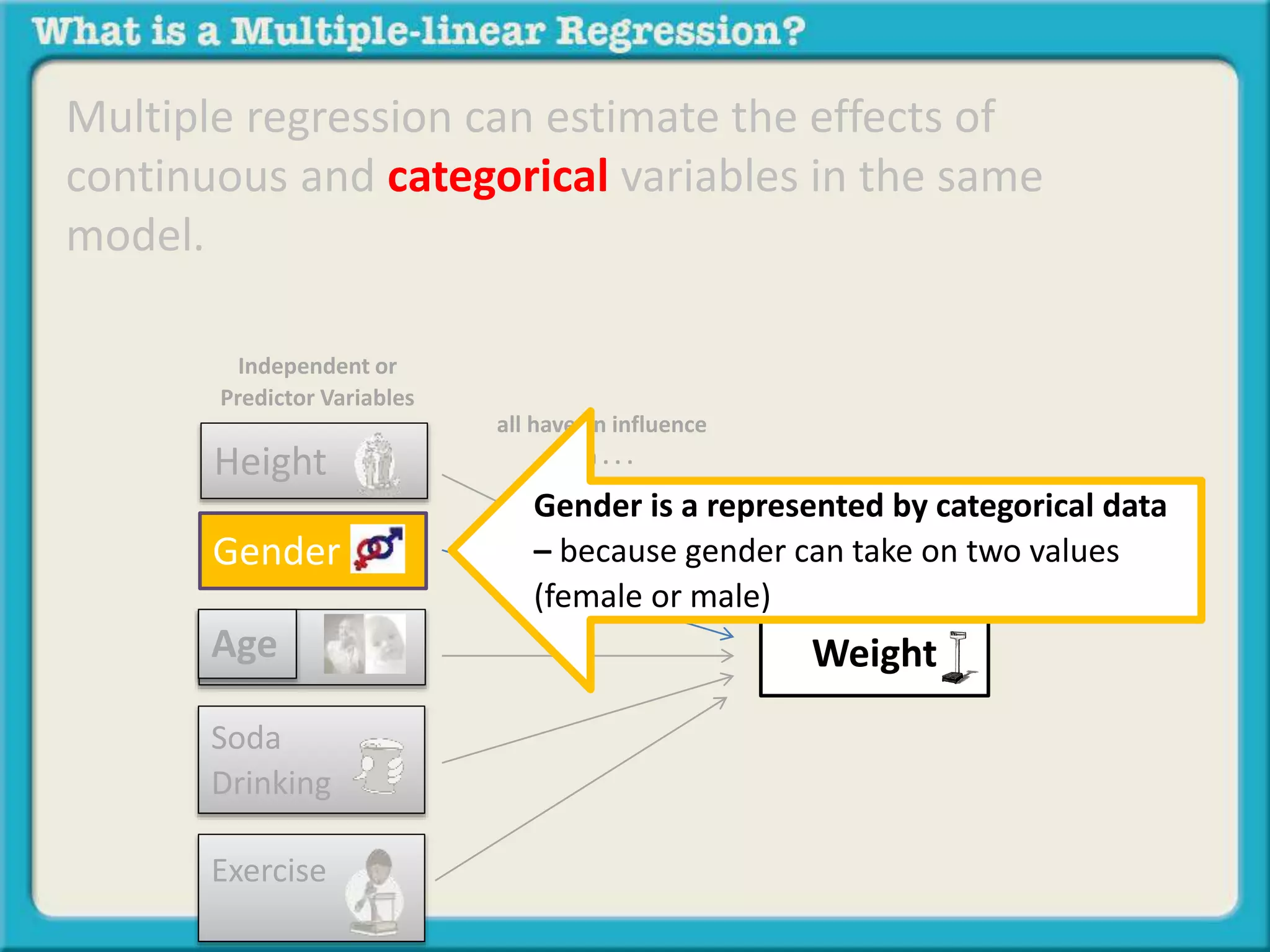
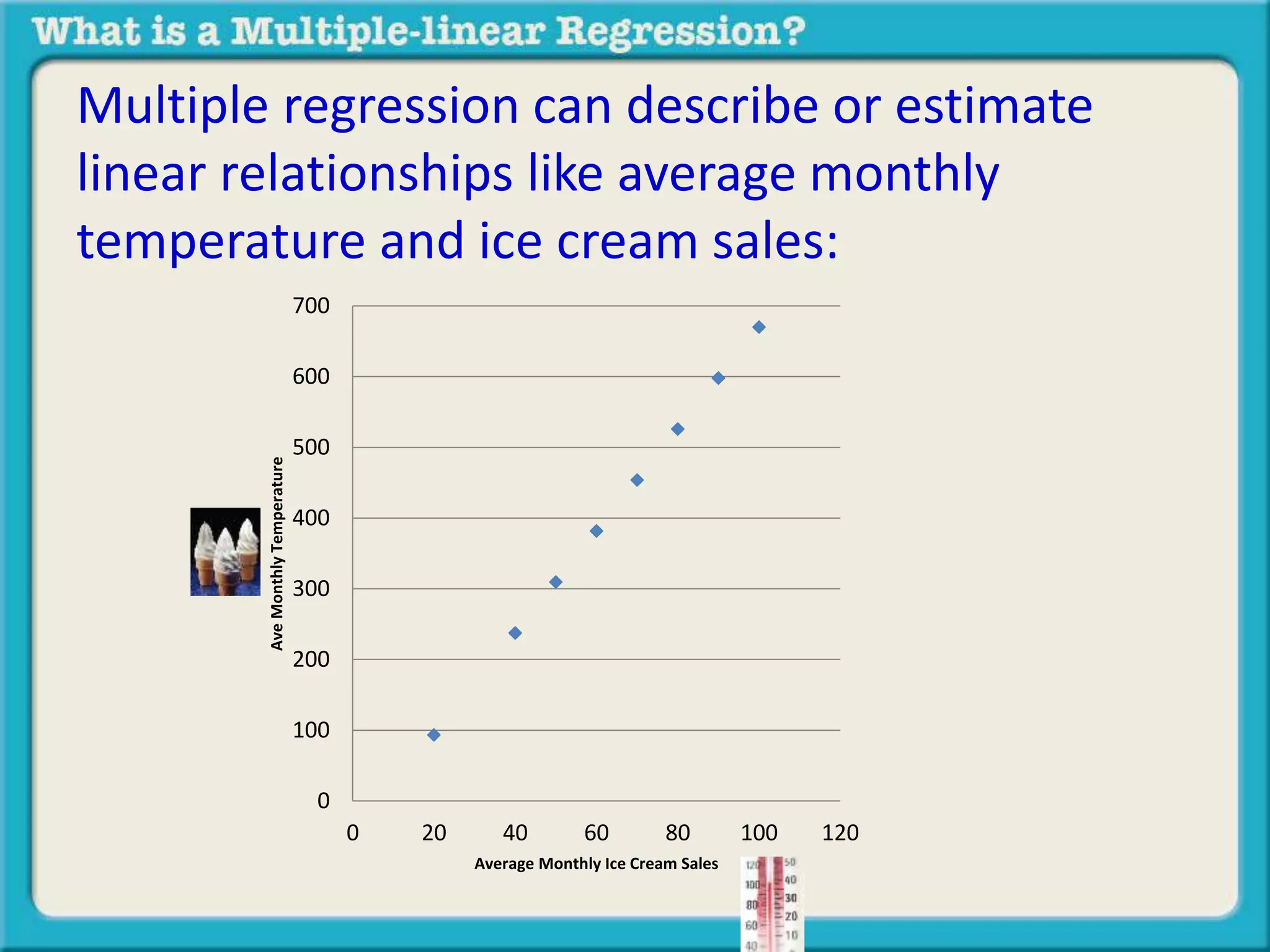
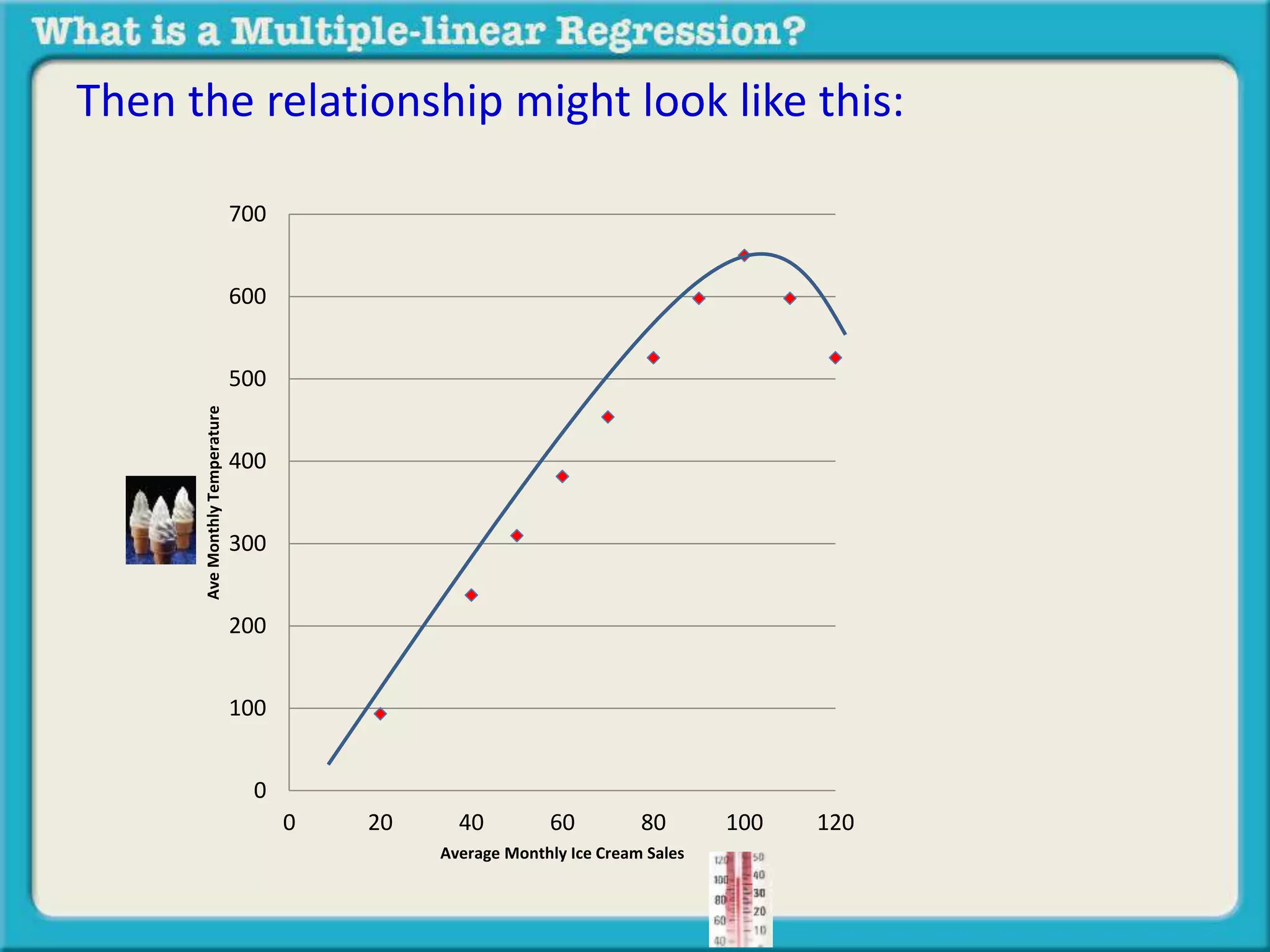
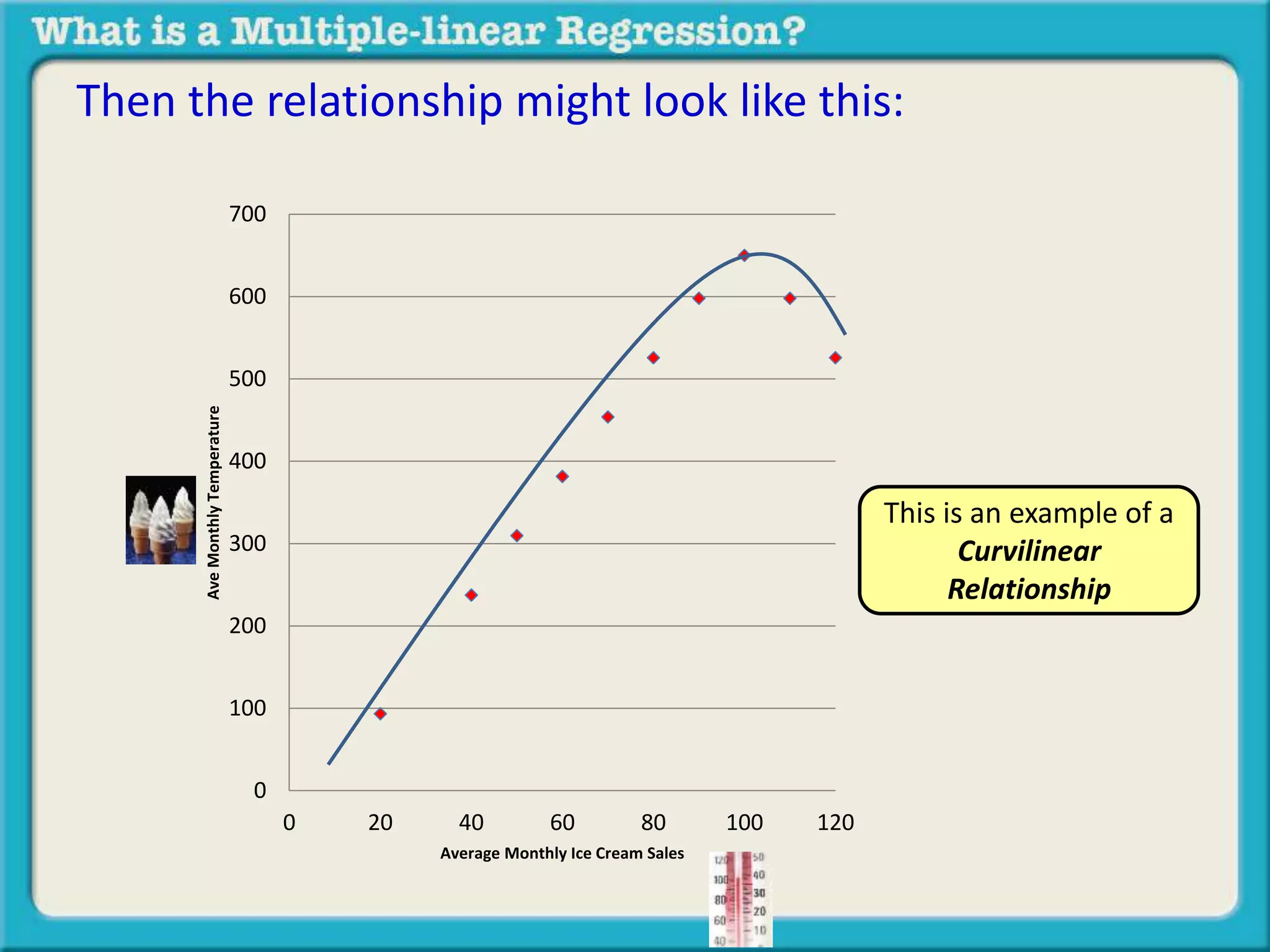
The document discusses multiple linear regression and partial correlation. It explains that multiple regression allows one to analyze the unique contribution of predictor variables to an outcome variable after accounting for the effects of other predictor variables. Partial correlation similarly examines the relationship between two variables while controlling for a third, but only considers two variables, whereas multiple regression examines the effects of multiple predictor variables simultaneously. Examples are given comparing the correlation between height and weight with and without controlling for other relevant variables like gender, age, exercise habits, etc.

Education◦

Embed presentation

Downloaded 416 times
1 / 101
2 / 101
Most read
3 / 101
4 / 101
Most read
5 / 101
Most read
6 / 101
7 / 101
8 / 101
9 / 101
10 / 101
11 / 101
12 / 101
13 / 101
14 / 101
15 / 101
16 / 101
17 / 101
18 / 101
19 / 101
20 / 101
21 / 101
22 / 101
23 / 101
24 / 101
25 / 101
26 / 101
27 / 101
28 / 101
29 / 101
30 / 101
31 / 101
32 / 101
33 / 101
34 / 101
35 / 101
36 / 101
37 / 101
38 / 101
39 / 101
40 / 101
41 / 101
42 / 101
43 / 101
44 / 101
45 / 101
46 / 101
47 / 101
48 / 101
49 / 101
50 / 101
51 / 101
52 / 101
53 / 101
54 / 101
55 / 101
56 / 101
57 / 101
58 / 101
59 / 101
60 / 101
61 / 101
62 / 101
63 / 101
64 / 101
65 / 101
66 / 101
67 / 101
68 / 101
69 / 101
70 / 101
71 / 101
72 / 101
73 / 101
74 / 101
75 / 101
76 / 101
77 / 101
78 / 101
79 / 101
80 / 101
81 / 101
82 / 101
83 / 101
84 / 101
85 / 101
86 / 101
87 / 101
88 / 101
89 / 101
90 / 101
91 / 101
92 / 101
93 / 101
94 / 101
95 / 101
96 / 101
97 / 101
98 / 101
99 / 101
100 / 101
101 / 101
What is a Multiple Linear Regression?
Welcome to this learning module on Multiple Linear Regression
In this presentation we will cover the following aspects of Multiple Regression:
In this presentation we will cover the following aspects of Multiple Regression: - Connection to Partial Correlation and ANCOVA
In this presentation we will cover the following aspects of Multiple Regression: - Connection to Partial Correlation and ANCOVA - Unique contribution of each variable
In this presentation we will cover the following aspects of Multiple Regression: - Connection to Partial Correlation and ANCOVA - Unique contribution of each variable - Contribution of all variables at the same time
In this presentation we will cover the following aspects of Multiple Regression: - Connection to Partial Correlation and ANCOVA - Unique contribution of each variable - Contribution of all variables at the same time - Type of data multiple regression can handle
In this presentation we will cover the following aspects of Multiple Regression: - Connection to Partial Correlation and ANCOVA - Unique contribution of each variable - Contribution of all variables at the same time - Type of data multiple regression can handle - Types of relationships multiple regression describes
In this presentation we will cover the following aspects of Multiple Regression: - Connection to Partial Correlation and ANCOVA - Unique contribution of each variable - Contribution of all variables at the same time - Type of data multiple regression can handle - Types of relationships multiple regression describes
In this presentation we will cover the following aspects of Multiple Regression: - Connection to Partial Correlation and ANCOVA - Unique contribution of each variable - Contribution of In all this variables presentation at the we same will time - Type of data multiple cover the regression concept of can Partial handle Correlation. - Types of relationships multiple regression describes
In this presentation we will cover the following aspects of Multiple Regression: - Connection to Partial Correlation and ANCOVA - Unique contribution of each variable - Contribution of all variables at the same time - Type of data multiple regression can handle - Types of relationships multiple regression describes After going through this presentation look at the presentation on Analysis of Covariance and consider what multiple regression and ANCOVA have in common.
In this presentation we will cover the following aspects of Multiple Regression: - Connection to Partial Correlation and ANCOVA - Unique contribution of each variable - Contribution of What all variables is a Partial at Correlation? the same time - Type of data multiple regression can handle - Types of relationships multiple regression describes
Partial correlation estimates the relationship between two variables while removing the influence of a third variable from the relationship.
Like in the example that follows,
Like in the example that follows, a Pearson Correlation between height and weight would yield a .825 correlation.
Like in the example that follows, a Pearson Correlation between height and weight would yield a .825 correlation. We might then control for gender (because we think being female or male has an effect on the relationship between height and weight).
However, when controlling for gender the correlation between height and weight drops to .770.
However, when controlling for gender the correlation between height and weight drops to .770. Individual Height (inches) Weight (pounds) Sex (1 – male, 2 – female) A 73 240 1 B 70 210 1 C 69 180 1 D 68 160 1 E 70 150 2 F 68 140 2 G 67 135 2 H 62 120 2
However, when controlling for gender the correlation between height and weight drops to .770. Individual Height (inches) Weight (pounds) Sex (1 – male, 2 – female) A 73 240 1 B 70 210 1 C 69 180 1 D 68 160 1 E 70 150 2 F 68 140 2 G 67 135 2 H 62 120 2
However, when controlling for gender the correlation between height and weight drops to .770. Individual Height (inches) Weight (pounds) Sex (1 – male, 2 – female) A 73 240 1 B 70 210 1 C 69 180 1 D 68 160 1 E 70 150 2 F 68 140 2 G 67 135 2 H 62 120 2 &
However, when controlling for gender the correlation between height and weight drops to .770. Individual Height (inches) Weight (pounds) Sex (1 – male, 2 – female) A 73 240 1 B 70 210 1 C 69 180 1 D 68 160 1 E 70 150 2 F 68 140 2 G 67 135 2 H 62 120 2 &
However, when controlling for gender the correlation between height and weight drops to .770. Individual Height (inches) Weight (pounds) Sex (1 – male, 2 – female) A 73 240 1 B 70 210 1 C 69 180 1 D 68 160 1 E 70 150 2 F 68 140 2 G 67 135 2 H 62 120 2 & controlling for
However, when controlling for gender the correlation between height and weight drops to .770. Individual Height (inches) Weight (pounds) Sex (1 – male, 2 – female) A 73 240 1 B 70 210 1 C 69 180 1 D 68 160 1 E 70 150 2 F 68 140 2 G 67 135 2 H 62 120 2 & controlling for
However, when controlling for gender the correlation between height and weight drops to .770. Individual Height (inches) Weight (pounds) Sex (1 – male, 2 – female) A 73 240 1 B 70 210 1 C 69 180 1 D 68 160 1 E 70 150 2 F 68 140 2 G 67 135 2 H 62 120 2 & controlling for = .770
This is very helpful because we may think two variables (height and weight) are highly correlated but we can determine if that correlation holds when we take out the effect of a third variable (gender).
While in partial correlation, only two variables are correlated while holding a third variable constant, in multiple regression several variables are grouped together to predict an outcome variable.
While in partial correlation, only two variables are correlated while holding a third variable constant, in multiple regression several variables are grouped together to predict an outcome variable Independent or Predictor Variables
While in partial correlation, only two variables are correlated while holding a third variable constant, in multiple regression several variables are grouped together to predict an outcome variable Independent or Predictor Variables Height
While in partial correlation, only two variables are correlated while holding a third variable constant, in multiple regression several variables are grouped together to predict an outcome variable Independent or Predictor Variables Height Gender
While in partial correlation, only two variables are correlated while holding a third variable constant, in multiple regression several variables are grouped together to predict an outcome variable Independent or Predictor Variables Height Gender Age
While in partial correlation, only two variables are correlated while holding a third variable constant, in multiple regression several variables are grouped together to predict an outcome variable Independent or Predictor Variables Height Gender Age Soda Drinking
While in partial correlation, only two variables are correlated while holding a third variable constant, in multiple regression several variables are grouped together to predict an outcome variable Independent or Predictor Variables Height Gender Age Soda Drinking Exercise
While in partial correlation, only two variables are correlated while holding a third variable constant, in multiple regression several variables are grouped together to predict an outcome variable Independent or Predictor Variables Height Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable
While in partial correlation, only two variables are correlated while holding a third variable constant, in multiple regression several variables are grouped together to predict an outcome variable Independent or Predictor Variables Height Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable Weight
While in partial correlation, only two variables are correlated while holding a third variable constant, in multiple regression several variables are grouped together to predict an outcome variable Independent or Predictor Variables Height Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable Weight all have an influence on . . .
While in partial correlation, only two variables are correlated while holding a third variable constant, in multiple regression several variables are grouped together to predict an outcome variable Independent or Predictor Variables Height Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable Weight all have an influence on . . .
While in partial correlation, only two variables are correlated while holding a third variable constant, in multiple regression several variables are grouped together to predict an outcome variable Independent or Predictor Variables Height Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable Weight all have an influence on . . .
While in partial correlation, only two variables are correlated while holding a third variable constant, in multiple regression several variables are grouped together to predict an outcome variable Independent or Predictor Variables Height Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable Weight all have an influence on . . .
While in partial correlation, only two variables are correlated while holding a third variable constant, in multiple regression several variables are grouped together to predict an outcome variable Independent or Predictor Variables Height Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable Weight all have an influence on . . .
While in partial correlation, only two variables are correlated while holding a third variable constant, in multiple regression several variables are grouped together to predict an outcome variable Independent or Predictor Variables Height Weight Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence on . . .
In this presentation we will cover the following aspects of Multiple Regression: - Connection to Partial Correlation and ANCOVA - Unique contribution of each variable - Contribution of all variables at the same time - Type of data multiple regression can handle - Types of relationships multiple regression describes
Essentially, the group of predictors are all covariates to each other. Independent or Predictor Variables Height Weight Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence on . . .
Meaning, Independent or Predictor Variables Height Weight Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence on . . .
Meaning, for example, Independent or Predictor Variables Height Weight Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence on . . .
Meaning, for example, that it is possible to identify the unique prediction power of height on weight Independent or Predictor Variables Height Weight Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence on . . .
Meaning, for example, that it is possible to identify the unique prediction power of height on weight Independent or Predictor Variables Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence Height on . . . Weight
Meaning, for example, that it is possible to identify the unique prediction power of height on weight after you’ve taken out the influence of all of the other predictors. Independent or Predictor Variables Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence Height on . . . Weight
Meaning, for example, that it is possible to identify the unique prediction power of height on weight after you’ve taken out the influence of all of the other predictors. Independent or Predictor Variables Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence Height on . . . Weight
For example, Independent or Predictor Variables Height Weight Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence on . . .
For example, here is the correlation between Height and Weight without controlling for all of the other variables. Independent or Predictor Variables Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence Height on . . . Weight
For example, here is the correlation between Height and Weight without controlling for all of the other variables. Independent or Predictor Variables Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence Height on . . . Weight Correlation = .825
However, Independent or Predictor Variables Height Weight Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence on . . .
However, here is the correlation between Height and Weight after taking out the effect of all of the other variables. Independent or Predictor Variables Height Weight Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence on . . .
However, here is the correlation between Height and Weight after taking out the effect of all of the other variables. Independent or Predictor Variables Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence on . . . Weight Height
However, here is the correlation between Height and Weight after taking out the effect of all of the other variables. Independent or Predictor Variables Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence Height on . . . Weight Correlation = .601
However, here is the correlation between Height and Weight after taking out the effect of all of the other variables. Independent or Predictor Variables Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence on . . . Weight Correlation = .601 So, after eliminating the effect of gender, age, soda, and exercise on weight, the unique correlation that height shares with weight is .601. Height
Even though we were only correlating height and weight when we computed a correlation of .825,
Even though we were only correlating height and weight when we computed a correlation of .825, the other four variables still had an influence on weight.
Even though we were only correlating height and weight when we computed a correlation of .825, the other four variables still had an influence on weight. However, that influence was not accounted for and remained hidden.
With multiple regression we can control for these four variables and account for their influence
With multiple regression we can control for these four variables and account for their influence thus calculating the unique contribution height makes on weight without their influence being present.
We can do the same for any of these other variables. Like the relationship between Gender and Weight.
We can do the same for any of these other variables. Like the relationship between Gender and Weight. Independent or Predictor Variables Height Age Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence on . . . Weight Gender
We can do the same for any of these other variables. Like the relationship between Gender and Weight. Independent or Predictor Variables Height Age Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence on . . . Weight Gender Correlation = .701
But when you take out the influence of the other variables the correlation drops from .701 to .582.
BEFORE Independent or Predictor Variables Height Age Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence on . . . Weight Gender Correlation = .701
AFTER
AFTER Independent or Predictor Variables Height Age Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence on . . . Weight Gender
AFTER Independent or Predictor Variables Height Age Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence on . . . Weight Gender Correlation = .582
Here is the correlation between age and weight before you take out the effect of the other variables:
Here is the correlation between age and weight before you take out the effect of the other variables: Independent or Predictor Variables Height Gender Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence on . . . Age Weight
Here is the correlation between age and weight before you take out the effect of the other variables: Independent or Predictor Variables Height Gender Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence on . . . Age Weight Correlation = .435
The correlation drops from .435 to .385 after taking out the influence of the other variables:
The correlation drops from .435 to .385 after taking out the influence of the other variables: Independent or Predictor Variables Height Gender Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence on . . . Age Weight
The correlation drops from .435 to .385 after taking out the influence of the other variables: Independent or Predictor Variables Height Gender Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence on . . . Age Weight Correlation = .385
In this presentation we will cover the following aspects of Multiple Regression: - Connection to Partial Correlation and ANCOVA - Unique contribution of each variable - Contribution of all variables at the same time - Type of data multiple regression can handle - Types of relationships multiple regression describes
Beyond estimating the unique power of each predictor,
Beyond estimating the unique power of each predictor, multiple regression also estimates the combined power of the group of predictors.
Beyond estimating the unique power of each predictor, multiple regression also estimates the combined power of the group of predictors.
Beyond estimating the unique power of each predictor, multiple regression also estimates the combined power of the group of predictors. Independent or Predictor Variables Height Weight Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable
Beyond estimating the unique power of each predictor, multiple regression also estimates the combined power of the group of predictors. Independent or Predictor Variables Height Weight Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable Combined Correlation = .982
In this presentation we will cover the following aspects of Multiple Regression: - Connection to Partial Correlation and ANCOVA - Unique contribution of each variable - Contribution of all variables at the same time - Type of data multiple regression can handle - Types of relationships multiple regression describes
Multiple regression can estimate the effects of continuous and categorical variables in the same model.
Multiple regression can estimate the effects of continuous and categorical variables in the same model. Independent or Predictor Variables Height Dependent, Response or Outcome Variable Gender Age Soda Drinking Exercise Weight
Multiple regression can estimate the effects of continuous and categorical variables in the same model. Independent or Predictor Variables Height Height is represented by continuous data – because height can take on any value between two points in inches or centimeters. Dependent, Response or Outcome Variable Gender Age Soda Drinking Exercise Weight
Multiple regression can estimate the effects of continuous and categorical variables in the same model.
Multiple regression can estimate the effects of continuous and categorical variables in the same model. Independent or Predictor Variables Height Age Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence on . . . Weight Gender Gender is a represented by categorical data – because gender can take on two values (female or male)
In this presentation we will cover the following aspects of Multiple Regression: - Connection to Partial Correlation and ANCOVA - Unique contribution of each variable - Contribution of all variables at the same time - Type of data multiple regression can handle - Types of relationships multiple regression describes
Multiple regression can describe or estimate linear relationships like average monthly temperature and ice cream sales:
Multiple regression can describe or estimate linear relationships like average monthly temperature and ice cream sales: 700 600 500 400 300 200 100 0 0 20 40 60 80 100 120 Ave Monthly Temperature Average Monthly Ice Cream Sales
Multiple regression can describe or estimate linear relationships like average monthly temperature and ice cream sales: 700 600 500 400 300 200 100 0 0 20 40 60 80 100 120 Ave Monthly Temperature Average Monthly Ice Cream Sales
It can also describe or estimate curvilinear relationships.
For example,
For example, what if in our fantasy world the temperature reached 100 degrees and then 120 degrees. Let’s say with such extreme temperatures ice cream sales actually dip as consumers seek out products like electrolyte-enhanced drinks or slushies.
Then the relationship might look like this:
Then the relationship might look like this: 700 600 500 400 300 200 100 0 0 20 40 60 80 100 120 Ave Monthly Temperature Average Monthly Ice Cream Sales
Then the relationship might look like this: 700 600 500 400 300 200 100 0 0 20 40 60 80 100 120 Ave Monthly Temperature Average Monthly Ice Cream Sales This is an example of a Curvilinear Relationship
In summary,
In summary, Multiple Regression is like single linear regression but instead of determining the predictive power of one variable (temperature) on another variable (ice cream sales) we consider the predictive power of other variables (such as socio-economic status or age).
With multiple regression you can estimate the predictive power of many variables on a certain outcome,
With multiple regression you can estimate the predictive power of many variables on a certain outcome, as well as the unique influence each single variable makes on that outcome after taking out the influence of all of the other variables.

More Related Content

PPTX
What is a partial correlation?
byKen Plummer
 
ODP
Multiple Linear Regression II and ANOVA I
byJames Neill
 
PPTX
Regression analysis on SPSS
byAntimDevMishraMTechE
 
PDF
Multiple linear regression
byAvjinder (Avi) Kaler
 
PPTX
Regression analysis: Simple Linear Regression Multiple Linear Regression
byRavindra Nath Shukla
 
PPTX
Covariance vs Correlation
byAniruddha Deshmukh
 
PPTX
Multiple Linear Regression
byIndus University
 
PPT
Linear regression
byvermaumeshverma
 
What is a partial correlation?
byKen Plummer
 
Multiple Linear Regression II and ANOVA I
byJames Neill
 
Regression analysis on SPSS
byAntimDevMishraMTechE
 
Multiple linear regression
byAvjinder (Avi) Kaler
 
Regression analysis: Simple Linear Regression Multiple Linear Regression
byRavindra Nath Shukla
 
Covariance vs Correlation
byAniruddha Deshmukh
 
Multiple Linear Regression
byIndus University
 
Linear regression
byvermaumeshverma
 

What's hot

PPTX
Topic 5 Covariance & Correlation.pptx
byCallplanetsDeveloper
 
PDF
Correlation and Simple Regression
byVenkata Reddy Konasani
 
PDF
Categorical data analysis
bySumit Das
 
PPT
Linear regression
byKarishma Chaudhary
 
PPTX
Correlation and Regression
byRam Kumar Shah "Struggler"
 
PPT
multiple regression
byPriya Sharma
 
PPTX
Regression Analysis presentation by Al Arizmendez and Cathryn Lottier
byAl Arizmendez
 
PPS
Correlation and regression
byKhalid Aziz
 
PPTX
Regression Analysis
bySalim Azad
 
PPTX
Multiple Linear Regression
byVamshi krishna Guptha
 
PPTX
What is a Single Sample Z Test?
byKen Plummer
 
PPT
Time series slideshare
bySabbir Tahmidur Rahman
 
PDF
Probability Distributions
byCIToolkit
 
PPT
Regression analysis
byRavi shankar
 
PDF
Correlation and Regression Analysis using SPSS and Microsoft Excel
bySetia Pramana
 
PPTX
Descriptive statistics
byAileen Balbido
 
PPTX
Regression Analysis
byShiela Vinarao
 
PDF
Simple linear regression
byAvjinder (Avi) Kaler
 
PPT
Least square method
bySomya Bagai
 
PPTX
Sign test
bysukhpal0015
 
Topic 5 Covariance & Correlation.pptx
byCallplanetsDeveloper
 
Correlation and Simple Regression
byVenkata Reddy Konasani
 
Categorical data analysis
bySumit Das
 
Linear regression
byKarishma Chaudhary
 
Correlation and Regression
byRam Kumar Shah "Struggler"
 
multiple regression
byPriya Sharma
 
Regression Analysis presentation by Al Arizmendez and Cathryn Lottier
byAl Arizmendez
 
Correlation and regression
byKhalid Aziz
 
Regression Analysis
bySalim Azad
 
Multiple Linear Regression
byVamshi krishna Guptha
 
What is a Single Sample Z Test?
byKen Plummer
 
Time series slideshare
bySabbir Tahmidur Rahman
 
Probability Distributions
byCIToolkit
 
Regression analysis
byRavi shankar
 
Correlation and Regression Analysis using SPSS and Microsoft Excel
bySetia Pramana
 
Descriptive statistics
byAileen Balbido
 
Regression Analysis
byShiela Vinarao
 
Simple linear regression
byAvjinder (Avi) Kaler
 
Least square method
bySomya Bagai
 
Sign test
bysukhpal0015
 

Similar to Multiple linear regression

PPT
Multiple regression presentation
byCarlo Magno
 
PPTX
4.7 partial correlation
byRajeev Kumar
 
PPTX
Correlation and regression
bycbt1213
 
PPTX
Correlation and Regression.pptx
byJayaprakash985685
 
PPTX
Regression & correlation coefficient
byMuhamamdZiaSamad
 
PPTX
Correlation
byUniversity of the Punjab
 
PPTX
Presentation1.pptx
bymanuelposas
 
PPTX
Module 4- Correlation & Regression Analysis.pptx
byKishlay Kumar
 
PPT
"Understanding Correlation and Regression: Key Concepts for Data Analysis"
byRekhaBoraChatare
 
PPTX
Applied statistics part 4
byMohammad Hadi Farjoo MD, PhD, Shahid behehsti University of Medical Sciences
 
PPT
Ebd1 lecture 8 2010
byReko Kemo
 
DOCX
BUS308 Week 4 Lecture 1 Examining Relationships Expect.docx
bycurwenmichaela
 
PPT
Biostatistics lecture notes 7.ppt
byletayh2016
 
DOCX
RegressionMaking predictions using dataLimitations.docx
bydebishakespeare
 
DOCX
BUS308 Week 4 Lecture 1 Examining Relationships Expect.docx
byjasoninnes20
 
DOCX
BUS308 Week 4 Lecture 1 Examining Relationships Expect.docx
byrichardnorman90310
 
PPT
biv_mult.ppt
byPerumalPitchandi
 
PDF
S1 pb
byInternational advisers
 
DOCX
Chapter 9Multivariable MethodsObjectives• .docx
byspoonerneddy
 
PPTX
4_Correlation and and Regression (1).pptx
bysahibkoh
 
Multiple regression presentation
byCarlo Magno
 
4.7 partial correlation
byRajeev Kumar
 
Correlation and regression
bycbt1213
 
Correlation and Regression.pptx
byJayaprakash985685
 
Regression & correlation coefficient
byMuhamamdZiaSamad
 
Correlation
byUniversity of the Punjab
 
Presentation1.pptx
bymanuelposas
 
Module 4- Correlation & Regression Analysis.pptx
byKishlay Kumar
 
"Understanding Correlation and Regression: Key Concepts for Data Analysis"
byRekhaBoraChatare
 
Applied statistics part 4
byMohammad Hadi Farjoo MD, PhD, Shahid behehsti University of Medical Sciences
 
Ebd1 lecture 8 2010
byReko Kemo
 
BUS308 Week 4 Lecture 1 Examining Relationships Expect.docx
bycurwenmichaela
 
Biostatistics lecture notes 7.ppt
byletayh2016
 
RegressionMaking predictions using dataLimitations.docx
bydebishakespeare
 
BUS308 Week 4 Lecture 1 Examining Relationships Expect.docx
byjasoninnes20
 
BUS308 Week 4 Lecture 1 Examining Relationships Expect.docx
byrichardnorman90310
 
biv_mult.ppt
byPerumalPitchandi
 
S1 pb
byInternational advisers
 
Chapter 9Multivariable MethodsObjectives• .docx
byspoonerneddy
 
4_Correlation and and Regression (1).pptx
bysahibkoh
 

More from Ken Plummer

PPTX
Normal or skewed distributions (inferential) - Copyright updated
byKen Plummer
 
PPTX
Normal or skewed distributions (descriptive both2) - Copyright updated
byKen Plummer
 
PPTX
Levels of the iv
byKen Plummer
 
PPTX
Diff rel gof-fit - jejit - practice (5)
byKen Plummer
 
PPTX
Inferential vs descriptive tutorial of when to use - Copyright Updated
byKen Plummer
 
PPTX
Ordinal and nominal
byKen Plummer
 
PPTX
Independent variables (2)
byKen Plummer
 
PPTX
Relationship covariates
byKen Plummer
 
PPTX
Relationship nature of data
byKen Plummer
 
PPTX
Ordinal (ties)
byKen Plummer
 
PPTX
Dichotomous or scaled
byKen Plummer
 
PPTX
Skewed sample size less than 30
byKen Plummer
 
PPTX
Learn About Range - Copyright updated
byKen Plummer
 
PPTX
Nature of the data (spread) - Copyright updated
byKen Plummer
 
PPTX
Number of variables (predictive)
byKen Plummer
 
PPTX
Nature of the data (descriptive) - Copyright updated
byKen Plummer
 
PPTX
Diff rel ind-fit practice - Copyright Updated
byKen Plummer
 
PPTX
Skewed less than 30 (ties)
byKen Plummer
 
PPTX
Nature of the data practice - Copyright updated
byKen Plummer
 
PPTX
Mode practice 1 - Copyright updated
byKen Plummer
 
Normal or skewed distributions (inferential) - Copyright updated
byKen Plummer
 
Normal or skewed distributions (descriptive both2) - Copyright updated
byKen Plummer
 
Levels of the iv
byKen Plummer
 
Diff rel gof-fit - jejit - practice (5)
byKen Plummer
 
Inferential vs descriptive tutorial of when to use - Copyright Updated
byKen Plummer
 
Ordinal and nominal
byKen Plummer
 
Independent variables (2)
byKen Plummer
 
Relationship covariates
byKen Plummer
 
Relationship nature of data
byKen Plummer
 
Ordinal (ties)
byKen Plummer
 
Dichotomous or scaled
byKen Plummer
 
Skewed sample size less than 30
byKen Plummer
 
Learn About Range - Copyright updated
byKen Plummer
 
Nature of the data (spread) - Copyright updated
byKen Plummer
 
Number of variables (predictive)
byKen Plummer
 
Nature of the data (descriptive) - Copyright updated
byKen Plummer
 
Diff rel ind-fit practice - Copyright Updated
byKen Plummer
 
Skewed less than 30 (ties)
byKen Plummer
 
Nature of the data practice - Copyright updated
byKen Plummer
 
Mode practice 1 - Copyright updated
byKen Plummer
 

Recently uploaded

PPTX
Basics in Phytochemistry, Extraction, Isolation methods, Characterisation etc.
byD. Y. Patil College of Pharmacy, Kolhapur.
 
PDF
Analyzing the data of your initial survey
byThelma Villaflores
 
PPTX
Vitamins and mineral deficiency , signs and symptoms associated with exercise
byvirupa chandrika reddy
 
PDF
DHA/HAAD/MOH/DOH OPTOMETRY MCQ PYQ. .pdf
byAnmol Singh
 
PPTX
Details of Epithelial and Connective Tissue.pptx
byAshish Umale
 
PPTX
Pain. definition, causes, factor influencing pain & pain assessment.pptx
byPompi Begum
 
PDF
Projecte de la porta de la classe de primer A: Mar i cel.
byeduardrubio1
 
PDF
BỘ TEST KIỂM TRA CUỐI HỌC KÌ 1 - TIẾNG ANH 6-7-8-9 GLOBAL SUCCESS - PHIÊN BẢN...
byNguyen Thanh Tu Collection
 
PPTX
10-12-2025 Francois Staring How can Researchers and Initial Teacher Educators...
byEduSkills OECD
 
PPTX
Accounting Skills Paper-II (Registers of PACs and Credit Co-operative Societies)
byDr. Sushil Bansode
 
PDF
Biology Practical Class 12th 2025 PDF(2)-2-52.pdf
bySCPRPWomenCollegeChi
 
PDF
TOM STOPPARD (1937 - 2025) - THE MIND AS A STAGE, THE STAGE AS DESTINY .pdf
byMilanStankovic19
 
PPTX
How to Manage Reception Report in Odoo 18 Inventory
byCeline George
 
PDF
The voice of the rain poem class 11th.pdf
byReeta Baral
 
PDF
Toward Massive, Ultrareliable, and Low-Latency Wireless Communication With Sh...
byMan_Ebook
 
PPTX
Campfens "The Data Qualify Challenge: Publishers, institutions, and funders r...
byNational Information Standards Organization (NISO)
 
PPTX
Kochi MuleSoftMeetup_UnlockingMCPServer.pptx
bysandeepmenon62
 
PPTX
York "Collaboration for Research Support at U-M Library"
byNational Information Standards Organization (NISO)
 
PPTX
Limpitlaw "Licensing: From Mindset to Milestones"
byNational Information Standards Organization (NISO)
 
PPTX
Semester 6 unit 2 Atopic dermatitis.pptx
bysachin7989
 
Basics in Phytochemistry, Extraction, Isolation methods, Characterisation etc.
byD. Y. Patil College of Pharmacy, Kolhapur.
 
Analyzing the data of your initial survey
byThelma Villaflores
 
Vitamins and mineral deficiency , signs and symptoms associated with exercise
byvirupa chandrika reddy
 
DHA/HAAD/MOH/DOH OPTOMETRY MCQ PYQ. .pdf
byAnmol Singh
 
Details of Epithelial and Connective Tissue.pptx
byAshish Umale
 
Pain. definition, causes, factor influencing pain & pain assessment.pptx
byPompi Begum
 
Projecte de la porta de la classe de primer A: Mar i cel.
byeduardrubio1
 
BỘ TEST KIỂM TRA CUỐI HỌC KÌ 1 - TIẾNG ANH 6-7-8-9 GLOBAL SUCCESS - PHIÊN BẢN...
byNguyen Thanh Tu Collection
 
10-12-2025 Francois Staring How can Researchers and Initial Teacher Educators...
byEduSkills OECD
 
Accounting Skills Paper-II (Registers of PACs and Credit Co-operative Societies)
byDr. Sushil Bansode
 
Biology Practical Class 12th 2025 PDF(2)-2-52.pdf
bySCPRPWomenCollegeChi
 
TOM STOPPARD (1937 - 2025) - THE MIND AS A STAGE, THE STAGE AS DESTINY .pdf
byMilanStankovic19
 
How to Manage Reception Report in Odoo 18 Inventory
byCeline George
 
The voice of the rain poem class 11th.pdf
byReeta Baral
 
Toward Massive, Ultrareliable, and Low-Latency Wireless Communication With Sh...
byMan_Ebook
 
Campfens "The Data Qualify Challenge: Publishers, institutions, and funders r...
byNational Information Standards Organization (NISO)
 
Kochi MuleSoftMeetup_UnlockingMCPServer.pptx
bysandeepmenon62
 
York "Collaboration for Research Support at U-M Library"
byNational Information Standards Organization (NISO)
 
Limpitlaw "Licensing: From Mindset to Milestones"
byNational Information Standards Organization (NISO)
 
Semester 6 unit 2 Atopic dermatitis.pptx
bysachin7989
 

Multiple linear regression

  • 1.
    What is aMultiple Linear Regression?
  • 2.
    Welcome to thislearning module on Multiple Linear Regression
  • 3.
    In this presentationwe will cover the following aspects of Multiple Regression:
  • 4.
    In this presentationwe will cover the following aspects of Multiple Regression: - Connection to Partial Correlation and ANCOVA
  • 5.
    In this presentationwe will cover the following aspects of Multiple Regression: - Connection to Partial Correlation and ANCOVA - Unique contribution of each variable
  • 6.
    In this presentationwe will cover the following aspects of Multiple Regression: - Connection to Partial Correlation and ANCOVA - Unique contribution of each variable - Contribution of all variables at the same time
  • 7.
    In this presentationwe will cover the following aspects of Multiple Regression: - Connection to Partial Correlation and ANCOVA - Unique contribution of each variable - Contribution of all variables at the same time - Type of data multiple regression can handle
  • 8.
    In this presentationwe will cover the following aspects of Multiple Regression: - Connection to Partial Correlation and ANCOVA - Unique contribution of each variable - Contribution of all variables at the same time - Type of data multiple regression can handle - Types of relationships multiple regression describes
  • 9.
    In this presentationwe will cover the following aspects of Multiple Regression: - Connection to Partial Correlation and ANCOVA - Unique contribution of each variable - Contribution of all variables at the same time - Type of data multiple regression can handle - Types of relationships multiple regression describes
  • 10.
    In this presentationwe will cover the following aspects of Multiple Regression: - Connection to Partial Correlation and ANCOVA - Unique contribution of each variable - Contribution of In all this variables presentation at the we same will time - Type of data multiple cover the regression concept of can Partial handle Correlation. - Types of relationships multiple regression describes
  • 11.
    In this presentationwe will cover the following aspects of Multiple Regression: - Connection to Partial Correlation and ANCOVA - Unique contribution of each variable - Contribution of all variables at the same time - Type of data multiple regression can handle - Types of relationships multiple regression describes After going through this presentation look at the presentation on Analysis of Covariance and consider what multiple regression and ANCOVA have in common.
  • 12.
    In this presentationwe will cover the following aspects of Multiple Regression: - Connection to Partial Correlation and ANCOVA - Unique contribution of each variable - Contribution of What all variables is a Partial at Correlation? the same time - Type of data multiple regression can handle - Types of relationships multiple regression describes
  • 13.
    Partial correlation estimatesthe relationship between two variables while removing the influence of a third variable from the relationship.
  • 14.
    Like in theexample that follows,
  • 15.
    Like in theexample that follows, a Pearson Correlation between height and weight would yield a .825 correlation.
  • 16.
    Like in theexample that follows, a Pearson Correlation between height and weight would yield a .825 correlation. We might then control for gender (because we think being female or male has an effect on the relationship between height and weight).
  • 17.
    However, when controllingfor gender the correlation between height and weight drops to .770.
  • 18.
    However, when controllingfor gender the correlation between height and weight drops to .770. Individual Height (inches) Weight (pounds) Sex (1 – male, 2 – female) A 73 240 1 B 70 210 1 C 69 180 1 D 68 160 1 E 70 150 2 F 68 140 2 G 67 135 2 H 62 120 2
  • 19.
    However, when controllingfor gender the correlation between height and weight drops to .770. Individual Height (inches) Weight (pounds) Sex (1 – male, 2 – female) A 73 240 1 B 70 210 1 C 69 180 1 D 68 160 1 E 70 150 2 F 68 140 2 G 67 135 2 H 62 120 2
  • 20.
    However, when controllingfor gender the correlation between height and weight drops to .770. Individual Height (inches) Weight (pounds) Sex (1 – male, 2 – female) A 73 240 1 B 70 210 1 C 69 180 1 D 68 160 1 E 70 150 2 F 68 140 2 G 67 135 2 H 62 120 2 &
  • 21.
    However, when controllingfor gender the correlation between height and weight drops to .770. Individual Height (inches) Weight (pounds) Sex (1 – male, 2 – female) A 73 240 1 B 70 210 1 C 69 180 1 D 68 160 1 E 70 150 2 F 68 140 2 G 67 135 2 H 62 120 2 &
  • 22.
    However, when controllingfor gender the correlation between height and weight drops to .770. Individual Height (inches) Weight (pounds) Sex (1 – male, 2 – female) A 73 240 1 B 70 210 1 C 69 180 1 D 68 160 1 E 70 150 2 F 68 140 2 G 67 135 2 H 62 120 2 & controlling for
  • 23.
    However, when controllingfor gender the correlation between height and weight drops to .770. Individual Height (inches) Weight (pounds) Sex (1 – male, 2 – female) A 73 240 1 B 70 210 1 C 69 180 1 D 68 160 1 E 70 150 2 F 68 140 2 G 67 135 2 H 62 120 2 & controlling for
  • 24.
    However, when controllingfor gender the correlation between height and weight drops to .770. Individual Height (inches) Weight (pounds) Sex (1 – male, 2 – female) A 73 240 1 B 70 210 1 C 69 180 1 D 68 160 1 E 70 150 2 F 68 140 2 G 67 135 2 H 62 120 2 & controlling for = .770
  • 25.
    This is veryhelpful because we may think two variables (height and weight) are highly correlated but we can determine if that correlation holds when we take out the effect of a third variable (gender).
  • 26.
    While in partialcorrelation, only two variables are correlated while holding a third variable constant, in multiple regression several variables are grouped together to predict an outcome variable.
  • 27.
    While in partialcorrelation, only two variables are correlated while holding a third variable constant, in multiple regression several variables are grouped together to predict an outcome variable Independent or Predictor Variables
  • 28.
    While in partialcorrelation, only two variables are correlated while holding a third variable constant, in multiple regression several variables are grouped together to predict an outcome variable Independent or Predictor Variables Height
  • 29.
    While in partialcorrelation, only two variables are correlated while holding a third variable constant, in multiple regression several variables are grouped together to predict an outcome variable Independent or Predictor Variables Height Gender
  • 30.
    While in partialcorrelation, only two variables are correlated while holding a third variable constant, in multiple regression several variables are grouped together to predict an outcome variable Independent or Predictor Variables Height Gender Age
  • 31.
    While in partialcorrelation, only two variables are correlated while holding a third variable constant, in multiple regression several variables are grouped together to predict an outcome variable Independent or Predictor Variables Height Gender Age Soda Drinking
  • 32.
    While in partialcorrelation, only two variables are correlated while holding a third variable constant, in multiple regression several variables are grouped together to predict an outcome variable Independent or Predictor Variables Height Gender Age Soda Drinking Exercise
  • 33.
    While in partialcorrelation, only two variables are correlated while holding a third variable constant, in multiple regression several variables are grouped together to predict an outcome variable Independent or Predictor Variables Height Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable
  • 34.
    While in partialcorrelation, only two variables are correlated while holding a third variable constant, in multiple regression several variables are grouped together to predict an outcome variable Independent or Predictor Variables Height Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable Weight
  • 35.
    While in partialcorrelation, only two variables are correlated while holding a third variable constant, in multiple regression several variables are grouped together to predict an outcome variable Independent or Predictor Variables Height Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable Weight all have an influence on . . .
  • 36.
    While in partialcorrelation, only two variables are correlated while holding a third variable constant, in multiple regression several variables are grouped together to predict an outcome variable Independent or Predictor Variables Height Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable Weight all have an influence on . . .
  • 37.
    While in partialcorrelation, only two variables are correlated while holding a third variable constant, in multiple regression several variables are grouped together to predict an outcome variable Independent or Predictor Variables Height Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable Weight all have an influence on . . .
  • 38.
    While in partialcorrelation, only two variables are correlated while holding a third variable constant, in multiple regression several variables are grouped together to predict an outcome variable Independent or Predictor Variables Height Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable Weight all have an influence on . . .
  • 39.
    While in partialcorrelation, only two variables are correlated while holding a third variable constant, in multiple regression several variables are grouped together to predict an outcome variable Independent or Predictor Variables Height Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable Weight all have an influence on . . .
  • 40.
    While in partialcorrelation, only two variables are correlated while holding a third variable constant, in multiple regression several variables are grouped together to predict an outcome variable Independent or Predictor Variables Height Weight Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence on . . .
  • 41.
    In this presentationwe will cover the following aspects of Multiple Regression: - Connection to Partial Correlation and ANCOVA - Unique contribution of each variable - Contribution of all variables at the same time - Type of data multiple regression can handle - Types of relationships multiple regression describes
  • 42.
    Essentially, the groupof predictors are all covariates to each other. Independent or Predictor Variables Height Weight Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence on . . .
  • 43.
    Meaning, Independent or Predictor Variables Height Weight Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence on . . .
  • 44.
    Meaning, for example, Independent or Predictor Variables Height Weight Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence on . . .
  • 45.
    Meaning, for example,that it is possible to identify the unique prediction power of height on weight Independent or Predictor Variables Height Weight Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence on . . .
  • 46.
    Meaning, for example,that it is possible to identify the unique prediction power of height on weight Independent or Predictor Variables Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence Height on . . . Weight
  • 47.
    Meaning, for example,that it is possible to identify the unique prediction power of height on weight after you’ve taken out the influence of all of the other predictors. Independent or Predictor Variables Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence Height on . . . Weight
  • 48.
    Meaning, for example,that it is possible to identify the unique prediction power of height on weight after you’ve taken out the influence of all of the other predictors. Independent or Predictor Variables Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence Height on . . . Weight
  • 49.
    For example, Independentor Predictor Variables Height Weight Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence on . . .
  • 50.
    For example, hereis the correlation between Height and Weight without controlling for all of the other variables. Independent or Predictor Variables Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence Height on . . . Weight
  • 51.
    For example, hereis the correlation between Height and Weight without controlling for all of the other variables. Independent or Predictor Variables Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence Height on . . . Weight Correlation = .825
  • 52.
    However, Independent or Predictor Variables Height Weight Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence on . . .
  • 53.
    However, here isthe correlation between Height and Weight after taking out the effect of all of the other variables. Independent or Predictor Variables Height Weight Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence on . . .
  • 54.
    However, here isthe correlation between Height and Weight after taking out the effect of all of the other variables. Independent or Predictor Variables Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence on . . . Weight Height
  • 55.
    However, here isthe correlation between Height and Weight after taking out the effect of all of the other variables. Independent or Predictor Variables Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence Height on . . . Weight Correlation = .601
  • 56.
    However, here isthe correlation between Height and Weight after taking out the effect of all of the other variables. Independent or Predictor Variables Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence on . . . Weight Correlation = .601 So, after eliminating the effect of gender, age, soda, and exercise on weight, the unique correlation that height shares with weight is .601. Height
  • 57.
    Even though wewere only correlating height and weight when we computed a correlation of .825,
  • 58.
    Even though wewere only correlating height and weight when we computed a correlation of .825, the other four variables still had an influence on weight.
  • 59.
    Even though wewere only correlating height and weight when we computed a correlation of .825, the other four variables still had an influence on weight. However, that influence was not accounted for and remained hidden.
  • 60.
    With multiple regressionwe can control for these four variables and account for their influence
  • 61.
    With multiple regressionwe can control for these four variables and account for their influence thus calculating the unique contribution height makes on weight without their influence being present.
  • 62.
    We can dothe same for any of these other variables. Like the relationship between Gender and Weight.
  • 63.
    We can dothe same for any of these other variables. Like the relationship between Gender and Weight. Independent or Predictor Variables Height Age Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence on . . . Weight Gender
  • 64.
    We can dothe same for any of these other variables. Like the relationship between Gender and Weight. Independent or Predictor Variables Height Age Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence on . . . Weight Gender Correlation = .701
  • 65.
    But when youtake out the influence of the other variables the correlation drops from .701 to .582.
  • 66.
    BEFORE Independent or Predictor Variables Height Age Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence on . . . Weight Gender Correlation = .701
  • 67.
  • 68.
    AFTER Independent or Predictor Variables Height Age Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence on . . . Weight Gender
  • 69.
    AFTER Independent or Predictor Variables Height Age Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence on . . . Weight Gender Correlation = .582
  • 70.
    Here is thecorrelation between age and weight before you take out the effect of the other variables:
  • 71.
    Here is thecorrelation between age and weight before you take out the effect of the other variables: Independent or Predictor Variables Height Gender Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence on . . . Age Weight
  • 72.
    Here is thecorrelation between age and weight before you take out the effect of the other variables: Independent or Predictor Variables Height Gender Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence on . . . Age Weight Correlation = .435
  • 73.
    The correlation dropsfrom .435 to .385 after taking out the influence of the other variables:
  • 74.
    The correlation dropsfrom .435 to .385 after taking out the influence of the other variables: Independent or Predictor Variables Height Gender Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence on . . . Age Weight
  • 75.
    The correlation dropsfrom .435 to .385 after taking out the influence of the other variables: Independent or Predictor Variables Height Gender Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence on . . . Age Weight Correlation = .385
  • 76.
    In this presentationwe will cover the following aspects of Multiple Regression: - Connection to Partial Correlation and ANCOVA - Unique contribution of each variable - Contribution of all variables at the same time - Type of data multiple regression can handle - Types of relationships multiple regression describes
  • 77.
    Beyond estimating theunique power of each predictor,
  • 78.
    Beyond estimating theunique power of each predictor, multiple regression also estimates the combined power of the group of predictors.
  • 79.
    Beyond estimating theunique power of each predictor, multiple regression also estimates the combined power of the group of predictors.
  • 80.
    Beyond estimating theunique power of each predictor, multiple regression also estimates the combined power of the group of predictors. Independent or Predictor Variables Height Weight Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable
  • 81.
    Beyond estimating theunique power of each predictor, multiple regression also estimates the combined power of the group of predictors. Independent or Predictor Variables Height Weight Gender Age Soda Drinking Exercise Dependent, Response or Outcome Variable Combined Correlation = .982
  • 82.
    In this presentationwe will cover the following aspects of Multiple Regression: - Connection to Partial Correlation and ANCOVA - Unique contribution of each variable - Contribution of all variables at the same time - Type of data multiple regression can handle - Types of relationships multiple regression describes
  • 83.
    Multiple regression canestimate the effects of continuous and categorical variables in the same model.
  • 84.
    Multiple regression canestimate the effects of continuous and categorical variables in the same model. Independent or Predictor Variables Height Dependent, Response or Outcome Variable Gender Age Soda Drinking Exercise Weight
  • 85.
    Multiple regression canestimate the effects of continuous and categorical variables in the same model. Independent or Predictor Variables Height Height is represented by continuous data – because height can take on any value between two points in inches or centimeters. Dependent, Response or Outcome Variable Gender Age Soda Drinking Exercise Weight
  • 86.
    Multiple regression canestimate the effects of continuous and categorical variables in the same model.
  • 87.
    Multiple regression canestimate the effects of continuous and categorical variables in the same model. Independent or Predictor Variables Height Age Soda Drinking Exercise Dependent, Response or Outcome Variable all have an influence on . . . Weight Gender Gender is a represented by categorical data – because gender can take on two values (female or male)
  • 88.
    In this presentationwe will cover the following aspects of Multiple Regression: - Connection to Partial Correlation and ANCOVA - Unique contribution of each variable - Contribution of all variables at the same time - Type of data multiple regression can handle - Types of relationships multiple regression describes
  • 89.
    Multiple regression candescribe or estimate linear relationships like average monthly temperature and ice cream sales:
  • 90.
    Multiple regression candescribe or estimate linear relationships like average monthly temperature and ice cream sales: 700 600 500 400 300 200 100 0 0 20 40 60 80 100 120 Ave Monthly Temperature Average Monthly Ice Cream Sales
  • 91.
    Multiple regression candescribe or estimate linear relationships like average monthly temperature and ice cream sales: 700 600 500 400 300 200 100 0 0 20 40 60 80 100 120 Ave Monthly Temperature Average Monthly Ice Cream Sales
  • 92.
    It can alsodescribe or estimate curvilinear relationships.
  • 93.
  • 94.
    For example, whatif in our fantasy world the temperature reached 100 degrees and then 120 degrees. Let’s say with such extreme temperatures ice cream sales actually dip as consumers seek out products like electrolyte-enhanced drinks or slushies.
  • 95.
    Then the relationshipmight look like this:
  • 96.
    Then the relationshipmight look like this: 700 600 500 400 300 200 100 0 0 20 40 60 80 100 120 Ave Monthly Temperature Average Monthly Ice Cream Sales
  • 97.
    Then the relationshipmight look like this: 700 600 500 400 300 200 100 0 0 20 40 60 80 100 120 Ave Monthly Temperature Average Monthly Ice Cream Sales This is an example of a Curvilinear Relationship
  • 98.
  • 99.
    In summary, MultipleRegression is like single linear regression but instead of determining the predictive power of one variable (temperature) on another variable (ice cream sales) we consider the predictive power of other variables (such as socio-economic status or age).
  • 100.
    With multiple regressionyou can estimate the predictive power of many variables on a certain outcome,
  • 101.
    With multiple regressionyou can estimate the predictive power of many variables on a certain outcome, as well as the unique influence each single variable makes on that outcome after taking out the influence of all of the other variables.