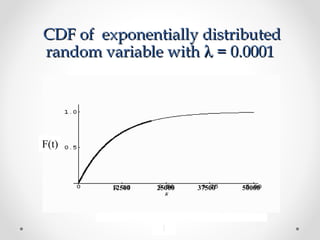
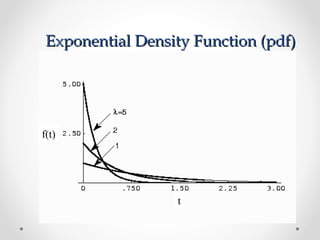
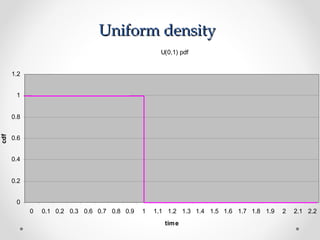
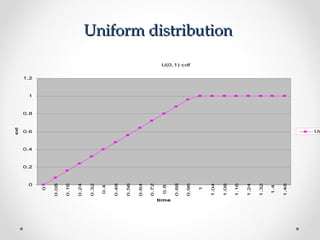
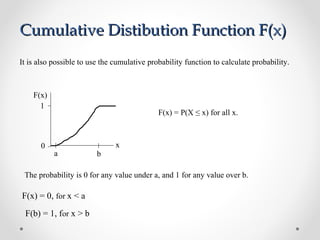
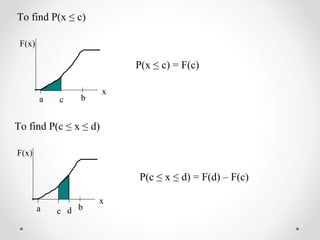
1) Continuous random variables have cumulative distribution functions (CDFs) that are continuous functions of the variable. They can have probability density functions (pdfs) that define their distributions. 2) Exponential distributions describe systems with memoryless properties where the probability of failure does not depend on past events. They commonly model time between events like packet arrivals. 3) Uniform distributions have constant pdfs across their range, resulting in a linear CDF ramp function. They are commonly used in random number generation.

1. Continuous Random VariablesContinuous Random Variables
Prepared By :
Patel Jay C
ME(EC)-140870705004

2. DefinitionsDefinitions
• Distribution function:
• If FX(x) is a continuous function of x, then X is a
continuous random variable.
o FX(x): discrete in x  Discrete rv’s
o FX(x): piecewise continuous  Mixed rv’s
•

3. DefinitionsDefinitions
Equivalence:
• CDF (cumulative distribution function)
• PDF (probability distribution function)
• Distribution function
• FX(x) or FX(t) or F(t)

4. Probability Density Function (pdf)Probability Density Function (pdf)
• X : continuous rv, then,
• pdf properties:
1.
2.

5. DefinitionsDefinitions
• Equivalence: pdf
o probability density function
o density function
o density
o f(t) =
dt
dF
,)(
)()(
0∫
∫
=
=
∞−
t
t
dxxf
dxxftF
For a non-negative
random variable

6. Exponential DistributionExponential Distribution
• Arises commonly in reliability & queuing theory.
• A non-negative random variable
• It exhibits memoryless (Markov) property.
• Related to (the discrete) Poisson distribution
o Interarrival time between two IP packets (or voice calls)
o Time to failure, time to repair etc.
• Mathematically (CDF and pdf, respectively):

7. CDF of exponentially distributedCDF of exponentially distributed
random variable withrandom variable with λλ = 0.0001= 0.0001
t
F(t)
12500 25000 37500 50000

8. Exponential Density Function (pdf)Exponential Density Function (pdf)
f(t)
t

9. Memoryless propertyMemoryless property
• Assume X > t. We have observed that the component
has not failed until time t.
• Let Y = X - t , the remaining (residual) lifetime
• The distribution of the remaining life, Y, does not
depend on how long the component has been operating.
Distribution of Y is identical to that of X.

10. Memoryless propertyMemoryless property
• Assume X > t. We have observed that the component has
not failed until time t.
• Let Y = X - t , the remaining (residual) lifetime
y
t
e
tXP
tyXtP
tXtyXP
tXyYPyG
λ−
−=
>
+≤<
=
>+≤=
>≤=
1
)(
)(
)|(
)|()(

11. Memoryless propertyMemoryless property
• Thus Gt(y) is independent of t and is identical
to the original exponential distribution of X.
• The distribution of the remaining life does
not depend on how long the component has
been operating.
• Its eventual breakdown is the result of some
suddenly appearing failure, not of gradual
deterioration.

12. Uniform Random VariableUniform Random Variable
• All (pseudo) random generators generate
random deviates of U(0,1) distribution; that
is, if you generate a large number of
random variables and plot their empirical
distribution function, it will approach this
distribution in the limit.
• U(a,b)  pdf constant over the (a,b) interval
and CDF is the ramp function

13. Uniform densityUniform density
U(0,1) pdf
0
0.2
0.4
0.6
0.8
1
1.2
0 0.1 0.2 0.3 0.6 0.7 0.8 0.9 1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2 2.1 2.2
time
cdf

14. Uniform distributionUniform distribution
• The distribution function is given by:
{
0 , x < a,
F(x)= , a < x < b
1 , x > b.ab
ax
−
−

15. Uniform distributionUniform distribution
U(0,1) cdf
0
0.2
0.4
0.6
0.8
1
1.2
0
0.08
0.16
0.24
0.32
0.4
0.48
0.56
0.64
0.72
0.8
0.88
0.96
1
1.04
1.08
1.16
1.24
1.32
1.4
1.48
time
cdf
U(

16. a b
F(x)
x0
1
F(x) = 0, for x < a
F(b) = 1, for x > b
It is also possible to use the cumulative probability function to calculate probability.
The probability is 0 for any value under a, and 1 for any value over b.
F(x) = P(X ≤ x) for all x.
Cumulative Distibution Function F(x)Cumulative Distibution Function F(x)

17. a b
F(x)
x
To find P(x ≤ c)
c
c da b
F(x)
x
To find P(c ≤ x ≤ d)
P(x ≤ c) = F(c)
P(c ≤ x ≤ d) = F(d) – F(c)