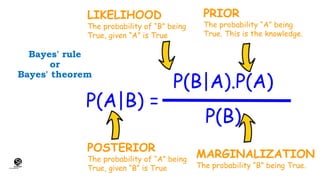
Bayes' theorem is a method for calculating conditional probabilities, linking the likelihood of events based on prior information. It incorporates new evidence to refine probability assessments and is fundamental to Bayesian statistics and probabilistic inference in AI. Applications include medical diagnosis, decision-making, and predictions in areas like weather forecasting.

1. Dr. C.V. Suresh Babu
(CentreforKnowledgeTransfer)
institute

2. Introduction
• Bayes' theorem is also known as Bayes' rule, Bayes' law, or Bayesian
reasoning, which determines the probability of an event with
uncertain knowledge.
• In probability theory, it relates the conditional probability and
marginal probabilities of two random events.
• Bayes' theorem was named after the British mathematician Thomas
Bayes. The Bayesian inference is an application of Bayes' theorem,
which is fundamental to Bayesian statistics.
(CentreforKnowledgeTransfer)
institute

3. What is Bayes Theorem?
• Bayes Theorem is a method of calculating conditional probability.
• The traditional method of calculating conditional probability (the
probability that one event occurs given the occurrence of a different
event) is to use the conditional probability formula, calculating the
joint probability of event one and event two occurring at the same
time, and then dividing it by the probability of event two occurring.
• However, conditional probability can also be calculated in a slightly
different fashion by using Bayes Theorem.
(CentreforKnowledgeTransfer)
institute

4. • When calculating conditional probability with Bayes theorem, you use the
following steps:
• Determine the probability of condition B being true, assuming that condition
A is true.
• Determine the probability of event A being true.
• Multiply the two probabilities together.
• Divide by the probability of event B occurring.
• This means that the formula for Bayes Theorem could be expressed like this:
P(A|B) = P(B|A)*P(A) / P(B)
• Calculating the conditional probability like this is especially useful when the
reverse conditional probability can be easily calculated, or when calculating
the joint probability would be too challenging.
(CentreforKnowledgeTransfer)
institute

5. How?
• It is a way to calculate the value of P(B|A) with the knowledge of
P(A|B)
• Bayes' theorem allows updating the probability prediction of an event
by observing new information of the real world.
• Example: If cancer corresponds to one's age then by using Bayes'
theorem, we can determine the probability of cancer more accurately
with the help of age.
(CentreforKnowledgeTransfer)
institute

6. Bayes' theorem
• Bayes' theorem can be derived using product rule and conditional probability of
event A with known event B:
• As from product rule we can write:
• P(A ⋀ B)= P(A|B) P(B) or
• imilarly, the probability of event B with known event A:
• P(A ⋀ B)= P(B|A) P(A)
• Equating right hand side of both the equations, we will get:
• The above equation (a) is called as Bayes' rule or Bayes' theorem. This equation
is basic of most modern AI systems for probabilistic inference.
(CentreforKnowledgeTransfer)
institute

7. Bayes' rule
or
Bayes' theorem
(CentreforKnowledgeTransfer)
institute

8. • It shows the simple relationship between joint and conditional
probabilities. Here,
• P(A|B) is known as posterior, which we need to calculate, and it will be
read as Probability of hypothesis A when we have occurred an evidence B.
• P(B|A) is called the likelihood, in which we consider that hypothesis is true,
then we calculate the probability of evidence.
• P(A) is called the prior probability, probability of hypothesis before
considering the evidence
• P(B) is called marginal probability, pure probability of an evidence.
• In the equation (a), in general, we can write P (B) = P(A)*P(B|Ai), hence the
Bayes' rule can be written as:
• Where A1, A2, A3,........, An is a set of mutually exclusive and exhaustive
events.
(CentreforKnowledgeTransfer)
institute

9. Applying Bayes' rule:
• Bayes' rule allows us to compute the single term P(B|A) in terms of
P(A|B), P(B), and P(A).
• This is very useful in cases where we have a good probability of these
three terms and want to determine the fourth one.
• Suppose we want to perceive the effect of some unknown cause, and
want to compute that cause, then the Bayes' rule becomes:
(CentreforKnowledgeTransfer)
institute

10. Example #1
Question: what is the probability that a patient has diseases meningitis with a
stiff neck?
Given Data:
• A doctor is aware that disease meningitis causes a patient to have a stiff neck,
and it occurs 80% of the time.
• He is also aware of some more facts, which are given as follows:
• The Known probability that a patient has meningitis disease is 1/30,000.
• The Known probability that a patient has a stiff neck is 2%.
Let a be the proposition that patient has stiff neck and b be the proposition that
patient has meningitis. , so we can calculate the following as:
 P(a|b) = 0.8
 P(b) = 1/30000
 P(a)= .02
Hence, we can assume that 1 patient out of 750 patients has meningitis
disease with a stiff neck.
(CentreforKnowledgeTransfer)
institute

11. Example #2:
• Question: From a standard deck of playing cards, a single card is drawn. The probability
that the card is king is 4/52, then calculate posterior probability P(King|Face), which
means the drawn face card is a king card.
• Solution:
• P(king): probability that the card is King= 4/52= 1/13
• P(face): probability that a card is a face card= 3/13
• P(Face|King): probability of face card when we assume it is a king = 1
• Putting all values in equation (i) we will get:
(CentreforKnowledgeTransfer)
institute

12. • Imagine you are a financial analyst at an investment bank. According to your research of publicly-
traded companies, 60% of the companies that increased their share price by more than 5% in the
last three years replaced their CEOs during the period.
• At the same time, only 35% of the companies that did not increase their share price by more
than 5% in the same period replaced their CEOs. Knowing that the probability that the stock
prices grow by more than 5% is 4%, find the probability that the shares of a company that fires
its CEO will increase by more than 5%.
• Before finding the probabilities, you must first define the notation of the probabilities.
• P(A) – the probability that the stock price increases by 5%
• P(B) – the probability that the CEO is replaced
• P(A|B) – the probability of the stock price increases by 5% given that the CEO has been replaced
• P(B|A) – the probability of the CEO replacement given the stock price has increased by 5%.
• Using the Bayes’ theorem, we can find the required probability:
Example #3:
Thus, the probability that the shares of a company that replaces its CEO will grow by more
than 5% is 6.67%.
(CentreforKnowledgeTransfer)
institute

13. • Using the cancer diagnosis example, we can show that Bayes rule allows us to obtain a much
better estimate.
• Now, we will put some made-up numbers into the example so we can assess the difference that
Bayes rule made.
• Assume that the probability of having cancer is 0.05 — meaning that 5% of people have cancer.
• Now, assume that the probability of being a smoker is 0.10 — meaning that 10% of people are
smokers, and that 20% of people with cancer are smokers, so P(smoker|cancer) = 0.20.
• Initially, our probability for cancer is simply our prior, so 0.05.
• However, using new evidence, we can instead calculate P(cancer|smoke), which is equal to
(P(smoker|cancer) * P(cancer)) / P(smoker) = (0.20 * 0.05) / (0.10) = 0.10.
• By introducing new evidence, we therefore obtained a better probability estimation.
• Initially we had a probability of 0.05, but using the smoker evidence, we were able to get to a
more accurate probability that was double our prior.
• In the given example (even with our made-up numbers), this effect should be quite logical, since
we know that smoking causes cancer.
This therefore demonstrates how Bayes rule allows us to update our beliefs using relevant
information.
Example #4:
(CentreforKnowledgeTransfer)
institute

14. Applications of Bayes' theorem
• It is used to calculate the next step of the robot when the already
executed step is given.
• Bayes' theorem is helpful in weather forecasting.
• It can solve the Monty Hall problem.
(CentreforKnowledgeTransfer)
institute