This document outlines basic probability concepts, including definitions of probability, views of probability (objective and subjective), and elementary properties. It discusses calculating probabilities of events from data in tables, including unconditional/marginal probabilities, conditional probabilities, and joint probabilities. Rules of probability are presented, including the multiplicative rule that the joint probability of two events is equal to the product of the marginal probability of one event and the conditional probability of the other event given the first event. Examples are provided to illustrate key concepts.














![Objective probability
b. Relative frequency or a posteriori probability
depends on repeatability of some process/ability to count
number of repetitions and number of times that the event
of interest occurs
■ If some process is repeated a large number of times, n,
and if some resulting event with the characteristic E
occurs m times, the relative frequency of occurrence of E,
m /n , will be approximately equal to the probability of E
P (E) = m /n [ m /n is an estimate of P (E) ]](https://image.slidesharecdn.com/basicprobabilityconcept-170623040142/75/Basic-probability-concept-15-2048.jpg)











![Rules of probability
1. Multiplicative rule
Joint probability can be calculated as the product of
appropriate marginal probability and appropriate conditional
probability
This relationship is known as multiplication rule of
probability
P (A ∩ B) = P (B) P (A | B), if P (B) ≠ 0
P (A ∩ B) = P (A) P (B | A), if P (A) ≠ 0
[ Note: P (B), P (A) are marginal probabilities ]](https://image.slidesharecdn.com/basicprobabilityconcept-170623040142/75/Basic-probability-concept-27-2048.jpg)
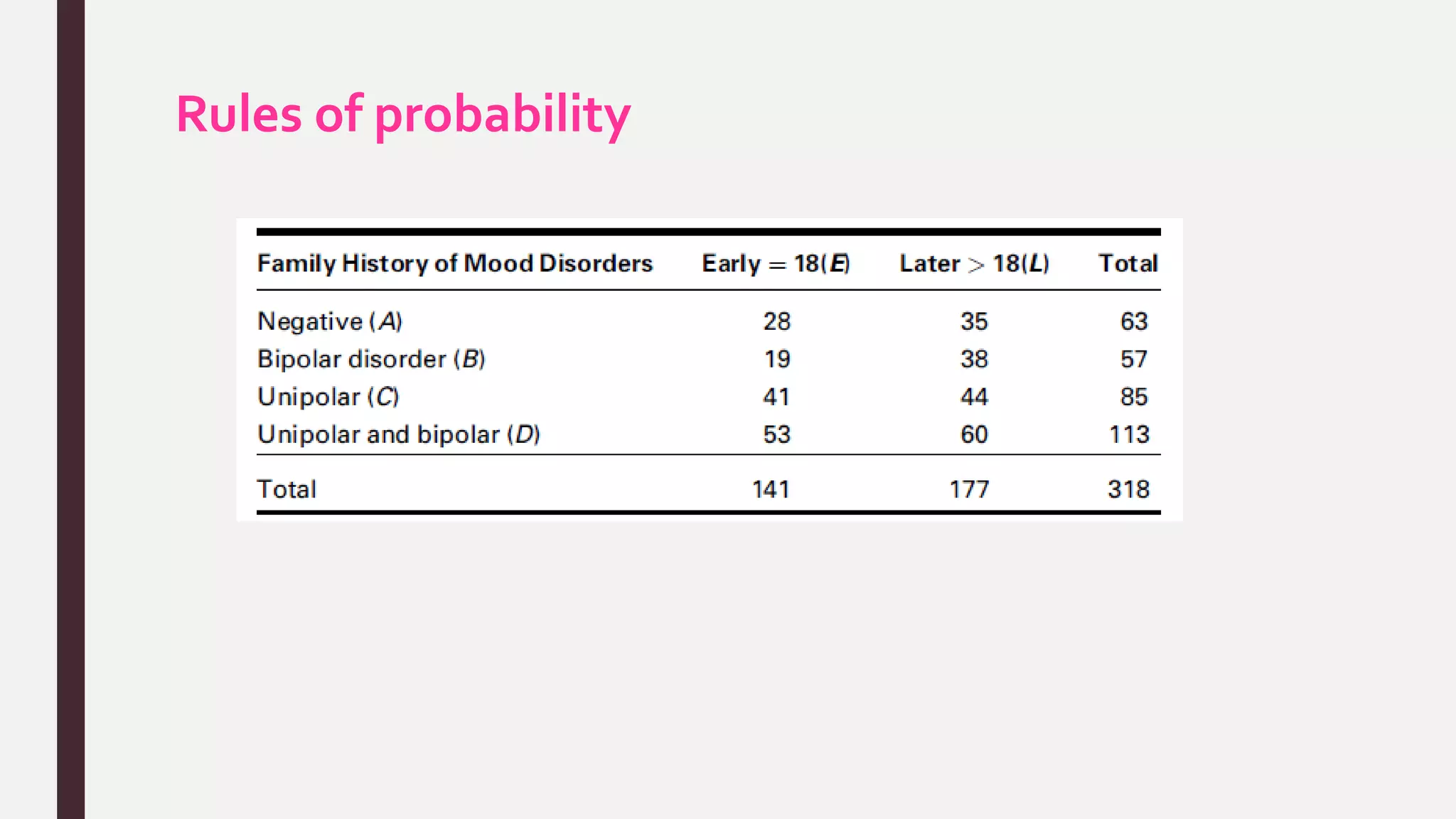



![Rules of probability
2. Additive rule
The probability of the occurrence of either one or the other of
two mutually exclusive events is equal to the sum of their
individual probabilities (Third property of probability)
The probability that a person will be early age (E) or later age
(L) = ?
P(E U L) = P (E) + P (L)
= 141/318 + 177/318
= 1
[Symbol ‘U’ is read as ‘union’ or ‘or’]](https://image.slidesharecdn.com/basicprobabilityconcept-170623040142/75/Basic-probability-concept-32-2048.jpg)



















![Normal Distribution
Also known as Gaussian distribution [Carl Friedrich Gauss (1777-1855)]
Normal density](https://image.slidesharecdn.com/basicprobabilityconcept-170623040142/75/Basic-probability-concept-52-2048.jpg)





