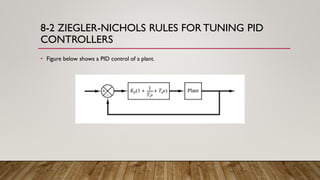
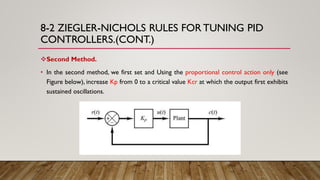
Chapter 8 discusses PID controllers, highlighting their prevalence in industry and various tuning methods including Ziegler-Nichols rules for tuning based on experimental step responses. The chapter emphasizes the utility of PID controls in scenarios where a plant's mathematical model is not known, and outlines both first and second methods for determining optimal controller parameters. It concludes that while Ziegler-Nichols rules provide a useful starting point for tuning PID controllers, further adjustments are often necessary to achieve desired performance.

1. CHAPTER 8
PID CONTROLLERS AND MODIFIED PID CONTROLLERS

2. 7-1 INTRODUCTION
• It is interesting to note that more than half of the industrial controllers in use today are
PID controllers or modified PID controllers.
• Because most PID controllers are adjusted on-site, many different types of tuning rules
have been proposed in the literature. Using these tuning rules, delicate and fine tuning of
PID controllers can be made on-site
• Also, automatic tuning methods have been developed and some of the PID controllers
may possess on-line automatic tuning capabilities. Modified forms of PID control, such as
I-PD control and multi-degrees-offreedom PID control, are currently in use in industry.

3. 7-1 INTRODUCTION(CONT.)
• Many practical methods for bumpless switching (from manual operation to automatic
operation) and gain scheduling are commercially available.
• The usefulness of PID controls lies in their general applicability to most control systems. In
particular, when the mathematical model of the plant is not known and therefore analytical design
methods cannot be used, PID controls prove to be most useful. In the field of process control
systems, it is well known that the basic and modified PID control schemes have proved their
usefulness in providing satisfactory control, although in many given situations they may not provide
optimal control.

4. 8-2 ZIEGLER-NICHOLS RULES FOR
TUNING PID CONTROLLERS

5. 8-2 ZIEGLER-NICHOLS RULES FOR TUNING PID
CONTROLLERS
• Figure below shows a PID control of a plant.

6. 8-2 ZIEGLER-NICHOLS RULES FOR TUNING PID
CONTROLLERS.(CONT.)
• If a mathematical model of the plant can be derived, then it is possible to apply various design techniques
for determining parameters of the controller that will meet the transient and steady-state specifications
of the closed-loop system.
• However, if the plant is so complicated that its mathematical model cannot be easily obtained, then an
analytical or computational approach to the design of a PID controller is not possible. Then we must
resort to experimental approaches to the tuning of PID controllers.
• The process of selecting the controller parameters to meet given performance specifications is known as
controller tuning. Ziegler and Nichols suggested rules for tuning PID controllers (meaning to set values
𝑘 𝑝, 𝑇𝑖 and 𝑇𝑑 ) based on experimental step responses or based on the value of 𝑘 𝑝that results in marginal
stability when only proportional control action is used.

7. 8-2 ZIEGLER-NICHOLS RULES FOR TUNING PID
CONTROLLERS.(CONT.)
• Ziegler–Nichols rules, which are briefly presented in the following, are useful when mathematical
models of plants are not known. (These rules can, of course, be applied to the design of systems
with known mathematical models.)
• Such rules suggest a set of values of 𝑘 𝑝, 𝑇𝑖 and 𝑇𝑑 that will give a stable operation of the system.
However, the resulting system may exhibit a large maximum overshoot in the step response, which
is unacceptable.
• However, the resulting system may exhibit a large maximum overshoot in the step response, which
is unacceptable.In such a case we need series of fine tunings until an acceptable result is obtained.

8. 8-2 ZIEGLER-NICHOLS RULES FOR TUNING PID
CONTROLLERS.(CONT.)
• . In fact, the Ziegler–Nichols tuning rules give an educated guess for the parameter values and
provide a starting point for fine tuning, rather than giving the final settings for 𝑘 𝑝, 𝑇𝑖 and 𝑇𝑑 in a
single shot.

9. 8-2 ZIEGLER-NICHOLS RULES FOR TUNING PID
CONTROLLERS.(CONT.)
Ziegler–Nichols Rules forTuning PID Controllers.
• Ziegler and Nichols proposed rules for determining values of the proportional gain integral
time and derivative time based on the transient response characteristics of a given plant.
• Such determination of the parameters of PID controllers or tuning of PID controllers can be
made by engineers on-site by experiments on the plant. (Numerous tuning rules for PID
controllers have been proposed since the Ziegler–Nichols proposal. They are available in the
literature and from the manufacturers of such controllers.)
• There are two methods called Ziegler–Nichols tuning rules: the first method and the second
method.We shall give a brief presentation of these two methods.

10. 8-2 ZIEGLER-NICHOLS RULES FOR TUNING PID
CONTROLLERS.(CONT.)
First Method.
• In the first method, we obtain experimentally the
response of the plant to a unit-step input, as shown in
Right Figure.
• If the plant involves neither integrator(s) nor
dominant complex-conjugate poles, then such a
unit-step response curve may look S-shaped, as shown in
Right Figure.

11. 8-2 ZIEGLER-NICHOLS RULES FOR TUNING PID
CONTROLLERS.(CONT.)
First Method.(Cont.)
• The S-shaped curve may be characterized by two constants, delay time L and time
constant T. The delay time and time constant are determined by drawing a tangent line at
the inflection point of the S-shaped curve and determining the intersections of the
tangent line with the time axis and line c(t)=K, as shown in previous Figure.

12. 8-2 ZIEGLER-NICHOLS RULES FOR TUNING PID
CONTROLLERS.(CONT.)
First Method.(Cont.)
• Table below Ziegler–Nichols Tuning Rule Based on Step Response of Plant (First Method)

13. 8-2 ZIEGLER-NICHOLS RULES FOR TUNING PID
CONTROLLERS.(CONT.)
Second Method.
• In the second method, we first set and Using the proportional control action only (see
Figure below), increase Kp from 0 to a critical value Kcr at which the output first exhibits
sustained oscillations.

14. 8-2 ZIEGLER-NICHOLS RULES FOR TUNING PID
CONTROLLERS.(CONT.)
Second Method.
• In the second method, we first set and Using the proportional control action only (see
Figure below), increase Kp from 0 to a critical value Kcr at which the output first exhibits
sustained oscillations. (If the output does not exhibit sustained oscillations for whatever
value Kp may take, then this method does not apply.).
• Thus, the critical gain Kcr and the corresponding period are experimentally determined.

15. 8-2 ZIEGLER-NICHOLS RULES FOR TUNING PID
CONTROLLERS.(CONT.)
Second Method.
• Table below Ziegler–Nichols Tuning Rule Based on Critical Gain Kcr and Critical Period
(Second Method)

16. 8-2 ZIEGLER-NICHOLS RULES FOR TUNING PID
CONTROLLERS.(CONT.)
Comments.
• Ziegler–Nichols tuning rules have been widely used to tune PID controllers in process
control systems where the plant dynamics are not precisely known. Over many years,
such tuning rules proved to be very useful. Ziegler–Nichols tuning rules can, of course, be
applied to plants whose dynamics are known.

17. Eng. Elaf Ahmed Saeed
Email: elafe1888@gmail.com
LinkedIn: https://www.linkedin.com/in/elaf-a-saeed
Facebook: https://www.facebook.com/profile.php?id=100004305557442
GitHub: https://github.com/ElafAhmedSaeed