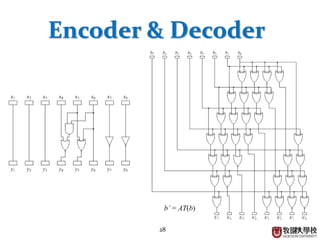
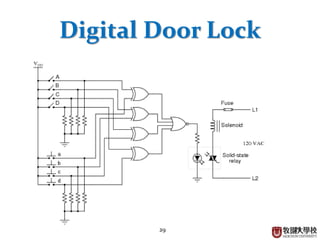
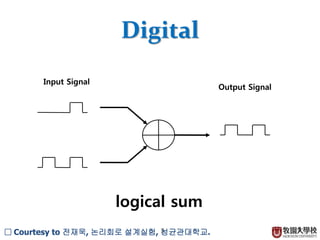
The document discusses combinational logic circuits. It begins with an introduction to analog and digital signals and binary number systems. It then covers Boolean algebra and logic gates such as AND, OR, NAND, NOR, XOR and XNOR. Combinational logic circuits are classified and examples like half adders, full adders, encoders and decoders are presented. One application discussed is a digital door lock circuit using logic gates.

1. Combinational Logic
Circuit
Yong Heui Cho @ Mokwon University
Some of slides are referred to:
[1] 전재욱, 논리회로 설계실험, 성균관대학교.
[2] Imran Waris, Digital and Logic Design, slideshare, 2014.

2. 2
Basic Computer Design
2. Introduction to Arduino
3. Basic Computer Architecture
4. Combinational Logic Circuit
5. Sequential Logic Circuit

3. 3
Analog & Digital
3
V
T
0
V
T
0
Analog (유사성) Digital (숫자 집합)
- Continuous @ time and amplitude
- Precise representation
- Sensitive to noise
- Old theory
□ Courtesy to 전재욱, 논리회로 설계실험, 성균관대학교.
- Discrete @ time or amplitude
- Approximate presentation
- Robust to noise
- Modern theory

4. 4
Analog
4
Input Signal
Output Signal
arithmetic sum
□ Courtesy to 전재욱, 논리회로 설계실험, 성균관대학교.

5. 5
Digital
5
Input Signal
Output Signal
logical sum
□ Courtesy to 전재욱, 논리회로 설계실험, 성균관대학교.

6. 6
Binary System
○ Binary System
– 0 or 1
– Notation: 10001001(2)
– Bit (binary digit)
– Byte = 8 bits
○ Decimal to Binary Conversion
6
652
32 … 1
16 … 0
08 … 0
04 … 0
02 … 0
01 … 0
2
2
2
2
2
1000001
128 64 32 16 8 4 2 1
0 1 0 0 0 0 0 1Binary :
□ Courtesy to 전재욱, 논리회로 설계실험, 성균관대학교.

7. 7
Power of 2
7
□ Courtesy to Imran Waris, Digital and Logic Design, slideshare.

8. 8
Decimal & Hexadecimal
8
□ Courtesy to Imran Waris, Digital and Logic Design, slideshare.

9. 9
Boolean Algebra
• Logical Sum : +
► A + B = Y
0 + 0 = 0
0 + 1 = 1
1 + 1 = 1
• Logical Product : •
► A • B = Y
0 • 0 = 0
0 • 1 = 0
1 • 1 = 1
• Logical Not : ~, ‾, n,’
► A ( ~A, nA, A’) = Y
0’ = 1
1’ = 0
9
A B Y
0 0 0
0 1 1
1 0 1
1 1 1
Truth Table
□ Courtesy to 전재욱, 논리회로 설계실험, 성균관대학교.

10. 10
Venn Diagram
10
XY
XY XY
□ Courtesy to 전재욱, 논리회로 설계실험, 성균관대학교.
John Venn

11. 11
De Morgan Law
11
A + B = A • B
A • B = A + B
□ Courtesy to 전재욱, 논리회로 설계실험, 성균관대학교.
Augustus
De Morgan

12. 12
Logic Signals
12
□ Courtesy to Imran Waris, Digital and Logic Design, slideshare.

13. 13
Buffer & NOT Gate
13
NOT Gate Buffer
Input Output
0 1
1 0
Input Output Input Output
Input Output
0 0
1 1
□ Courtesy to 전재욱, 논리회로 설계실험, 성균관대학교.

14. 14
Analog NOT Gate Circuit
14
Input
Output
B
C
E
B = 0
B = 1
□ Courtesy to 전재욱, 논리회로 설계실험, 성균관대학교.
A NOT gate is a transistor (TR)!

15. 15
Gate?
• Logic gate
– Physical device implementing a Boolean
function
• “Gate” is the terminal name of a vacuum
tube.
15

16. 16
AND & NAND Gate
16
AND Gate NAND (NOT + AND) Gate
Input A
Input B
Output
Input A
Input B
Output
Input A Input B Output
0 0 0
0 1 0
1 0 0
1 1 1
Input A Input B Output
0 0 1
0 1 1
1 0 1
1 1 0
□ Courtesy to 전재욱, 논리회로 설계실험, 성균관대학교.

17. 17
Analog AND Gate Circuit
17
B
C
E
=>
B
C E
Output
Input A Input B
< TR > < Switch >
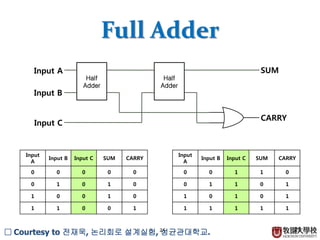
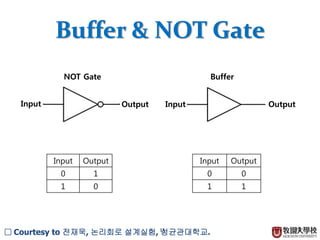
□ Courtesy to 전재욱, 논리회로 설계실험, 성균관대학교.
An AND gate is series wire connection!
+5 [V]

18. 18
OR & NOR Gate
18
OR Gate NOR (NOT + OR) Gate
Input A
Input B
Output
Input A
Input B
Output
Input A Input B Output
0 0 0
0 1 1
1 0 1
1 1 1
Input A Input B Output
0 0 1
0 1 0
1 0 0
1 1 0
□ Courtesy to 전재욱, 논리회로 설계실험, 성균관대학교.

19. 19
Analog OR Gate Circuit
19
Input A Input B
Output
□ Courtesy to 전재욱, 논리회로 설계실험, 성균관대학교.
An OR gate is parallel wire connection!
+5 [V]

20. 20
XOR & XNOR Gate
20
XOR (Exclusive OR) Gate XNOR Gate
Input A
Input B
Output
Input A
Input B
Output
Input A Input B Output
0 0 0
0 1 1
1 0 1
1 1 0
Input A Input B Output
0 0 1
0 1 0
1 0 0
1 1 1
A ⊙ B = YA B = Y
□ Courtesy to 전재욱, 논리회로 설계실험, 성균관대학교.

21. 21
Combinational Logic
21
Input A
Input B
Input C
Input D
Output
(A+B) (CD) = Output
□ Courtesy to 전재욱, 논리회로 설계실험, 성균관대학교.

22. 22
Classification
22

23. 23
Half Adder
23
Half
Adder
Input A
Input B
Sum
Carry
Input
A
Input B Sum Carry
0 0 0 0
0 1 1 0
1 0 1 0
1 1 0 1
0
+0
00
0
+1
01
1
+0
01
1
+1
10
0010011
+1000001
1010010
Half
Adder
Half
Adder
Half
Adder
Half
Adder
Half
Adder
Half
Adder
Half
Adder
Carry ?
□ Courtesy to 전재욱, 논리회로 설계실험, 성균관대학교.

24. 24
Circuit of Half Adder
24
Input A
Input B
SUM
CARRY
(A B) = SUM
A • B = CARRY
□ Courtesy to 전재욱, 논리회로 설계실험, 성균관대학교.

25. 25
Full Adder
25
Half
Adder
Half
Adder
Input A
Input B
SUM
CARRY
Input C
Input
A
Input B Input C SUM CARRY
0 0 0 0 0
0 1 0 1 0
1 0 0 1 0
1 1 0 0 1
Input
A
Input B Input C SUM CARRY
0 0 1 1 0
0 1 1 0 1
1 0 1 0 1
1 1 1 1 1
□ Courtesy to 전재욱, 논리회로 설계실험, 성균관대학교.

26. 26
Circuit of Full Adder
26
Carry
Input A
Input B SUM
Carry
Input
□ Courtesy to 전재욱, 논리회로 설계실험, 성균관대학교.

27. 27
Combination of Full Adder
27
Full
Adder
Half
Adder
Full
Adder
Full
Adder
Full
Adder
Full
Adder
Full
Adder
Full
Adder
A1 B1A2 B2A3 B3A4 B4A5 B5A6 B6A7 B7A8 B8
SUM1SUM2SUM3SUM4SUM5SUM6SUM7SUM8CARRY
10010011
+10010001
100100100
□ Courtesy to 전재욱, 논리회로 설계실험, 성균관대학교.

28. 28
Encoder & Decoder
28

29. 29
Digital Door Lock
29