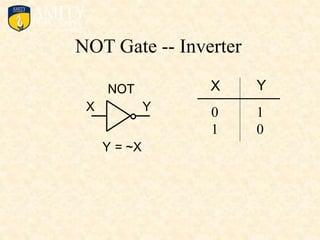
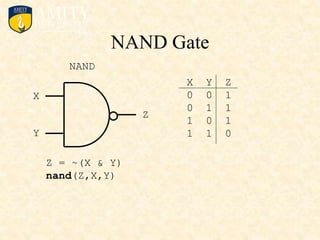
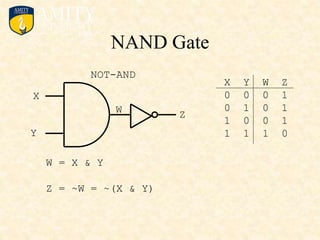
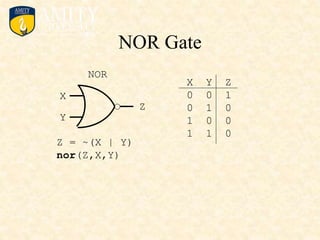
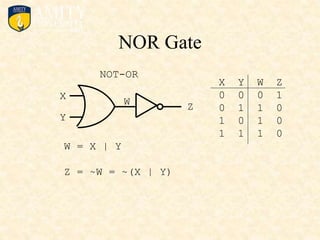
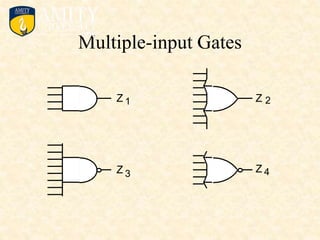
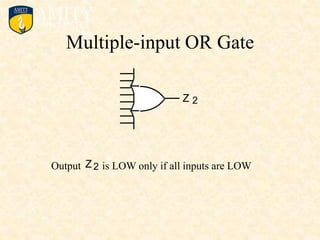
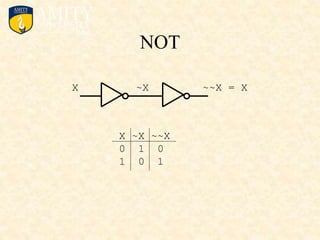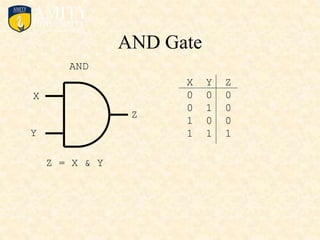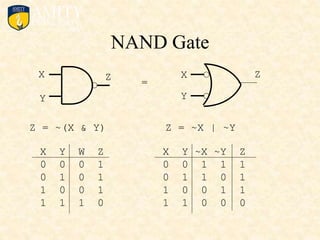This document outlines the syllabus for a Digital Electronics & Computer Organization Lab course. The syllabus includes simulations of basic logic circuits like half adders, full adders, and arithmetic logic units using ORCAD software. It also covers the study of the 8085 microprocessor instruction set and basic logic gates like AND, OR, NOT, NAND, NOR, XOR, and XNOR gates. Multiple-input logic gates are also discussed.

1. Digital Electronics & Computer
Organization Lab

2. Syllabus
• Simulation using ORCAD
• To simulate Half Adder circuit
• To simulate Full Adder Circuit
• To simulate the logical part of a simple Arithmetic logical Unit
• To simulate a 4-bit binary adder-subtractor circuit
• Simulation of one digit BCD Adder.
• To simulate and study the tristate buffer
• To simulate the common bus using tri-state buffers and decoder
• To simulate the common bus using multiplexers.
• Study of 8085Microprocessor
• Study of instruction set of 8085

3. Basic Logic Gates

4. Basic Logic Gates
and Basic Digital Design
• NOT, AND, and OR Gates
• NAND and NOR Gates
• Exclusive-OR (XOR) Gate
• Multiple-input Gates

5. NOT gate
• Referred to as an inverter
• Converts the input state to an opposite
output state
• Only two input combinations possible

6. NOT Gate -- Inverter
X Y
0
1
1
0
X Y
Y
NOT
X Y
Y = ~X
NOT

7. • Y = ~X (Verilog)
• Y = !X (ABEL)
• Y = not X (VHDL)
• Y = X’
• Y = X
• Y = X (textook)
• not(Y,X) (Verilog)
NOT

8. NOT
X ~X ~~X = X
X ~X ~~X
0 1 0
1 0 1

9. AND gate
• Two or more inputs and a single output
• Produces a 1 output only when all inputs are
1s
• Total number of possible combinations: N =
2power(n) where: n = total number of input
variables
• Performs basic operation of multiplication

10. AND Gate
AND
X
Y
Z
Z = X & Y
X Y Z
0 0 0
0 1 0
1 0 0
1 1 1

11. • X & Y (Verilog and ABEL)
• X and Y (VHDL)
• X Y
• X Y
• X * Y
• XY (textbook)
• and(Z,X,Y) (Verilog)
AND
U
V

12. OR gate
• Produces a 1 output if any of its inputs are
1s
• Performs basic operation of addition
• Can have any number of inputs greater than
one

13. OR Gate
OR
X
Y
Z
Z = X | Y
X Y Z
0 0 0
0 1 1
1 0 1
1 1 1

14. OR
• X | Y (Verilog)
• X # Y (ABEL)
• X or Y (VHDL)
• X + Y (textbook)
• X V Y
• X U Y
• or(Z,X,Y) (Verilog)

15. NAND gate
• Combination of an inverter and an AND
gate (NOT-AND)
• Most commonly used logic function
• Produces a 1 output when any of the inputs
are 0s
• Available with two, three, four, eight, and
thirteen inputs

16. NAND Gate
NAND
X
Y
Z
X Y Z
0 0 1
0 1 1
1 0 1
1 1 0
Z = ~(X & Y)
nand(Z,X,Y)

17. NAND Gate
NOT-AND
X
Y
Z
W = X & Y
Z = ~W = ~(X & Y)
X Y W Z
0 0 0 1
0 1 0 1
1 0 0 1
1 1 1 0
W

18. NOR gate
• Combination of an inverter and an OR gate
(NOT-OR)
• Produces a 1 output only when both inputs
are 0s
• Available with two, three, four, and eight
inputs

19. NOR Gate
NOR
X
Y
Z
X Y Z
0 0 1
0 1 0
1 0 0
1 1 0
Z = ~(X | Y)
nor(Z,X,Y)

20. NOR Gate
NOT-OR
X
Y
W = X | Y
Z = ~W = ~(X | Y)
X Y W Z
0 0 0 1
0 1 1 0
1 0 1 0
1 1 1 0
Z
W

21. NAND Gate
X
Y
X
Y
Z Z
Z = ~(X & Y) Z = ~X | ~Y
=
X Y W Z
0 0 0 1
0 1 0 1
1 0 0 1
1 1 1 0
X Y ~X ~Y Z
0 0 1 1 1
0 1 1 0 1
1 0 0 1 1
1 1 0 0 0

22. NOR Gate
X
Y
Z
Z = ~(X | Y)
X Y Z
0 0 1
0 1 0
1 0 0
1 1 0
X
Y
Z
Z = ~X & ~Y
X Y ~X ~Y Z
0 0 1 1 1
0 1 1 0 0
1 0 0 1 0
1 1 0 0 0

23. X-OR and X-NOR gates
Exclusive OR gate (XOR)
• Has only two inputs
• Produces a 1 output only if both inputs are
different
Exclusive NOR gate (XNOR)
• Complement of the XOR gate
• Produces a 1 output only when both inputs
are the same

24. Exclusive-OR Gate
X Y Z
XOR
X
Y
Z 0 0 0
0 1 1
1 0 1
1 1 0
Z = X ^ Y
xor(Z,X,Y)

25. XOR
• X ^ Y (Verilog)
• X $ Y (ABEL)
• X @ Y
• xor(Z,X,Y) (Verilog)
X Y (textbook)


26. Exclusive-NOR Gate
X Y Z
XNOR
X
Y
Z 0 0 1
0 1 0
1 0 0
1 1 1
Z = ~(X ^ Y)
Z = X ~^ Y
xnor(Z,X,Y)

27. XNOR
• X ~^ Y (Verilog)
• !(X $ Y) (ABEL)
• X @ Y
• xnor(Z,X,Y) (Verilog)
X Y

28. Multiple-input Gates
Z 1 2
3 4
Z Z
Z

29. Multiple-input AND Gate
Z 1
Output is HIGH only if all inputs are HIGH
Z1
An open input will float HIGH

30. Multiple-input OR Gate
Output is LOW only if all inputs are LOW
Z2
2
Z

31. Multiple-input NAND Gate
Output is LOW only if all inputs are HIGH
Z3
3
Z

32. Multiple-input NOR Gate
Output is HIGH only if all inputs are LOW
Z4
4
Z

33. Summary
• An AND gate produces a 1 output when all
of its inputs are 1s
• An OR gate produces a 1 output if any of its
inputs are 1s
• A NOT gate converts the input state to an
opposite output state
• A NAND gate produces a 1 output when
any of the inputs are 0s

34. Summary
• A NOR gate produces a 1 output only when
both inputs are 0s
• An exclusive OR (XOR) gate produces a 1
output only if both inputs are different
• An exclusive NOR (XNOR) gate produces
a 1 output only when both inputs are the
same

35. Any Questions?