Skip to main content
UploadLanguage (EN)Support
BusinessMobileSocial MediaMarketingTechnologyArt & PhotosCareerDesignEducationPresentations & Public SpeakingGovernment & NonprofitHealthcareInternetLawLeadership & ManagementAutomotiveEngineeringSoftwareRecruiting & HRRetailSalesServicesScienceSmall Business & EntrepreneurshipFoodEnvironmentEconomy & FinanceData & AnalyticsInvestor RelationsSportsSpiritualNews & PoliticsTravelSelf ImprovementReal EstateEntertainment & HumorHealth & MedicineDevices & HardwareLifestyle
Mirza Salman Baig, profile picture
Uploaded byMirza Salman Baig
PDF, PPTX1,156 views

Chemical kinetics v2

The document discusses various topics related to chemical kinetics including: - Rate of reaction is defined as the change in concentration of reactants or products over time. Rate laws relate the rate of reaction to the concentrations of reactants. - Reaction order refers to the sum of powers in the rate law. Molecularity is the actual number of reacting species. Pseudo-orders occur when one reactant is in excess. 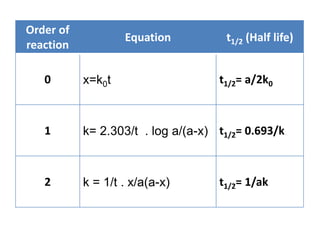- Rate constants have different units for different reaction orders. Integrated rate laws and the half-life method can be used to determine the order of a reaction experimentally. 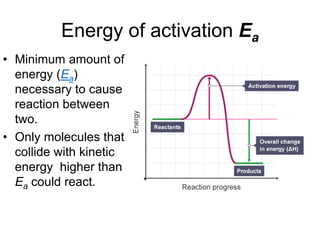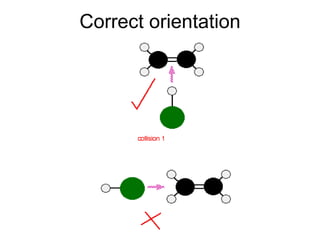- Collision theory states that molecules must collide with sufficient energy and correct orientation to react. Physical factors like temperature, solvent, and

Science◦
Download as PDF, PPTX
Chemical kinetics V2 (Dr.) Mirza Salman Baig Assistant Professor (Pharmaceutics) AIKTC, School of Pharmacy,New Panvel Affiliated to University of Mumbai (INDIA)
Rate of reaction • A → B • Rate of reaction is defined as the change in concentration of any of reactant or product per unit time. – Rate of reaction = Rate of disappearance of A – Rate of reaction = Rate of appearance of B • Unit = M/s • Rate= dA/dt
Rate of reaction • Rate of reaction = - d[A] /dt • Rate of reaction = + d[B] /dt
Rate law • The Equation which shows how rate is related to concentration Reaction • 2NO + 2H2 → N2 + 2H2O Rate Law • Rate of reaction = k[H2] [NO]2
Rate Law • The rate of reaction is directly proportional to the reactant concentration, each concentration being raised to some power. • 2A + B → Product • Rate =k[A]m[B]n (k = specific rate constant)
Order of reaction • Order of reaction is defined as sum of powers of concentration in rate law. • Rate =k[A]m[B]n • Order of reaction in above case is (m+n) • It is the number of concentration of chemical species which determine the rate of reaction depends.
Molecularity of reaction Number of molecules (chemical species) which take part in chemical reaction. It is number (integer) not a fraction. Types • Unimolecular cis to trans • Bimolecular A+B ---> C • Termolecular A+B+C --> D
Reaction Order • Sum of powers of concentration terms in rate law • Experimentally determined • It can have fractional value • It can assume zero value Molecularity • Number of reacting species in a reaction • Therotical concept • It is always a whole number • It cannot have zero value
Order of reaction wrt A
Overall order of reaction
First Order Reaction • A--> Product • At time t=0 concentration of reactant A is a mole/lit, • After time t, x mole of A have changed, the final concentration after time t will be (a-x) • For first order reaction dx/dt is directly proportional to (instantaneous) concentration of reactant... • dx/dt= k(a-x) • dx/(a-x)= kdt
First Order Reaction • dx/(a-x)= kdt …. (1) • Integrating above equation.. • ∫dx/(a-x)= ∫kdt • -ln (a-x) = kt + I …. (2) If t=0, x=0 then I= -ln a Substituting I in equation (2) • ln [a/(a-x)]= kt or k = (1/t) ln [a/(a-x)] • Converting it to common log • k = log
First Order Reaction • After integration • K= 2.303/t . Log a/(a-x) • k= 2.303/(t2-t1) . log (a-x1)/(a-x2) • t1 and t2 are time interval at which x1 and x2 amount of reactant changed respectively
Second Order Reaction Reaction A--> Product Initial conc a 0 Final conc a-x x • For second order reaction rate of reaction is proportional to square of concentration of reactants • dx/dt= k (a-x)2
Second Order Reaction • dx/dt= k (a-x)2 • dx/(a-x)2=k dt • On integration ∫ dx/(a-x)2= ∫k dt • 1/(a-x) = kt +I At t=0, x=0.... I = 1/a
Second Order Reaction • Substituting value of I in above equation • 1/(a-x) = kt + 1/a • kt = 1/(a-x) - 1/a • k = .
Zero Order reaction • Rate of reaction is independent of concentration of reactant/product • Time A --> Product • Initial conc 0 a 0 • Final conc t a-x x
Zero Order reaction • Rate of reaction = -d[A]/dt= k0[A]0 • dx/dt= k0 (a-x)0 • x=k0t • k0 is rate constant (or specific rate constant) of zero order reaction • Rate constant is the rate of reaction at all concentrations x/t
Pseudo order reaction • Experimental order of reaction which is not actual is known as pseudo order • Reaction A+B → Product • If B is in excesses, its concentration will practically constant and only concentration of A will affect rate of reaction hence rate law will be.. • Rate = k' [A]...
Pseudo order reaction (Example) • Ethyle acetate+ Water (excesses) --> Acetic acid + EtOH
Units of rate constant • Units of rate constant for different order reaction are different • For Zero order • k= d[A]/dt • k= mol/lit . 1/time • k= mol lit-1 time-1
Units of rate constant • For first order • k= 2.303/t . log a/(a-x) • k= 2.303/t . log [A]0/[A]t • k= 1/time • k= time-1
Units of rate constant • For second order reaction • k= 1/t . x/a(a-x) • k= 1/t . x/[A]0([A]0-x) • k= 1/time . concentration/concentration2 • k= 1/time . 1/concentration • k= 1/time . 1/(mol/lit) • k= mol-1 lit time-1
How to determine order of reaction • Using integrated rate equations • Graphical Method • Using half life period • Oswald isolation method
Using integrated rate equations • Perform the reaction using different initial concentration of of reactant (a) and note the concentration (a-x) at regular time intervals (t) • These values are then substituted in integrated rate equations (first order, second order, zero order) • The rate equation which yield constant value for k corrosponds to that order of reaction.
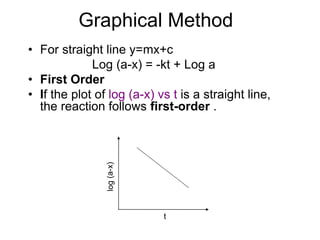
Graphical Method • For straight line y=mx+c Log (a-x) = -kt + Log a • First Order • If the plot of log (a-x) vs t is a straight line, the reaction follows first-order . t
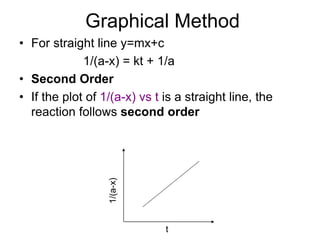
Graphical Method • For straight line y=mx+c 1/(a-x) = kt + 1/a • Second Order • If the plot of 1/(a-x) vs t is a straight line, the reaction follows second order t
Graphical Method x=k0t
Half life reaction • It is defined as the time required as for the decrease in concentration of reactant to half of its initial value. • When x= a/2, then time is termed as t1/2 • We can substitute this value in equation of reaction
Using Half life method • Seperate experiments should be performed using different initial concentration. Let initial concentration be A1 and A2 and corresponding half life t1 and t2 • Half life for nth order reaction is • t1/2→ 1/ [A] n-1
Using Half life method • Zero order: Half life is directly proportional to initial concentration of the reactants • First order: Half life is independent of the initial concentration of reactants • Second order: Half life is inversly proportional to initial cincentration of reactants
Order of reaction Equation t1/2 (Half life) 0 x=k0t t1/2= a/2k0 1 k= 2.303/t . log a/(a-x) t1/2= 0.693/k 2 k = 1/t . x/a(a-x) t1/2= 1/ak
Collision Theory of Reaction Rate • According to this theory, chemical reaction take place only when there is collision between reacting molecules. • Colliding molecules must possess enough kinetic energy • A-A + B-B --> 2 A-B • Molecules must collide with correct orientation
Energy of activation Ea • Minimum amount of energy (Ea) necessary to cause reaction between two. • Only molecules that collide with kinetic energy higher than Ea could react.
Correct orientation
Limitations of collision theory • It applies to simple gaseous reactions only • Values of rate constant (k) calculated by Arrhenius equation are in agreement with simple bimolecular reaction only (not for complex molecules) • Theory consider only (linier) kinetic energy but not rotational, vibrational energy. • Theory don’t speaks about breaking of bonds involved in it.
Physical and chemical factors influencing the chemical degradation of pharmaceutical product: • Temperature • Solvent & Dielectric constant • Ionic strength • Specific acid base catalysis • General acid base catalysis
Effect of Temperature (Arrhenius equation) • Rate of reaction increase 3-folds by increase in temperature by about 10oC • Relation between rate constant, temperature and Ea .....Arrhenius equation • k= Ae-Ea/RT • R= gas constant • T = Temperature in Kelvin • A= Factor related to frequency of collision • Ea= Energy of activation • e= mathematical const (Napier’s ) ≈ 2.71828
Effect of Temperature
Effect of Solvent • Rate of reaction will be fast if product is more soluble than reactant, in reaction solvent. • Rate of reaction will be slow if reactant are more soluble in solvent than product. • A→ B
Effect of solvent (Dielectric constant) • Reactions involving ions of opposit charge are accelerated by solvents with low dielectric constant (ability of a substance to store electrical energy in an electric field) • Ex. Rate of hydrolysis of sulphate ester is greater in low dielectric constant solvent like methylene chloride than in water. • Acid inversion of sucrose, rate of reaction increases if dielectric constant (of water ) reduced (by adding dioxane) • Reaction between similar charged ions is favoured by high dielectric constant solvents • Reaction between neutral molecules which produce highly polar transition state is favoured by high dielectric constant solvents
Effect of Ionic strength • Ionic strength may affect inter-ionic attraction • Increase in ionic strength expected to decrease (not favorable) rate of reaction between oppositely charged ions • Increase in ionic strength expected to Increase (favorable) rate of reaction between similar charged ions... as per Debye-Hukel equation
Catalyst • It is a substance that influence speed of reaction without itself being altered chemically. • When catalyst decrease rate of reaction then it is known as negative catalyst. Mechanism : • It may form intermediate complex with reactant • May produce free radicles like *CH3 • Homogeneous catalyst→ Catalyst and reactant are in same phase • Heterogeneous catalyst→ ex. Finely divided platinum
Specific acid base catalysis • Specific acid base catalysis refer to catalysis by hydrogen ion (H+) or Hydroxyl Ion (OH-) hence (H+ and OH-) terms involved in rate law. • Ex. Rate of hydrolysis of ester ethylacetate • CH3-COOC2H5 → CH3COOH + C2H5-OH • It is studied at constant pH (buffered soln), rate of disappearance of ethyl acetate (ester) will apparently First order. • If reaction is studied at different pH (in acidic range) then different first order rate constant k is observed at different pH.
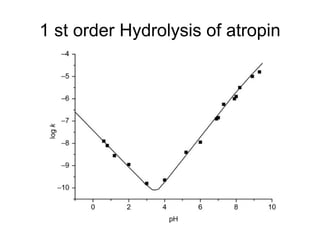
Specific acid base catalysis • Observed rate depend on concentration of ester and [H+], therefore it is actually second order reaction. • Observed rate constant (kobs) at different pH in acidic region, is proportional to [H+] • kobs = kacid [H+] • logkobs = log kacid + log [H+] • logkobs = log kacid - pH
Specific acid base catalysis • Log kobs = log kacid - pH • It suggest log kobs vs pH is straight line with slop -1 and y-intercept log kacid • If we study same reaction in alkaline pH then we observe different rate constant at different pH • log kobs = log kbase + log [OH-] • kobs = kacid[H+] + kbase [OH-]
1 st order Hydrolysis of atropin
General acid base catalysis • Acid or base catalysis is not restricted to effect of [H+] or [OH-] • Other components of buffer (which is generally used in pharma formulations) may cause catalysis. • Undissociated acid and base can often produce catalytic effect • Metal can also serve as catalyst • Ex. Mutarotation of glucose in acetate buffer is catalysed by [H+], [OH-], Acetate ion [CH3COO-], undissociated acid [CH3COOH] undissociated acetic acid.
Problem Q1. Solution of drug contained 500unit/ml of drug when prepared. It was analyzed after 40 days and found to contain 300 unit/ml. Assume decomposition is first order, at what time will the drug have decomposed to one half of its original concentration?
Ans 1 • a= 500 unit/ml • (a-x) = 300 unit/ml • t= 40 days • k= 2.303/t . log a/(a-X) • k= 2.303/40 . log 500/300 • k= 0.0576 × log 1.667 • k= 0.0576 × 0.222 • k= 0.01278 day-1
• t1/2 = 0.693/k .... for first order • t1/2 = 0.693/ 0.01278 • t1/2 = 54.23 Days
Problem • Q2 Consider the reaction: 2B → C + 3D. In one experiment it was found that at 300 K the rate constant is 0.134 L/(mol.s). A second experiment showed that at 450 K, the rate constant was 0.569 L/(mol.s). Determine the activation energy for the reaction
• Ans 2. • Ea = 10.8 kJ
Thank You