This document provides background information on reaction rates and mechanisms. It discusses how factors like reactant concentrations, temperature, catalysts, and surface area can influence reaction rates. It also defines concepts like the rate law, rate constant, reaction order, energy of activation, and Arrhenius equation. Methods for determining reaction order are described, including by varying reactant concentrations and analyzing integrated rate expressions for zero, first, and second order reactions. The effects of temperature on reaction rates are also addressed through the Arrhenius equation.

1. I. Background on Rates & Mechanisms
 Main Factors which influence reaction rate:
 Concentrations of Reactants - Rates usually increase as
reactant concentrations increase.
 Reaction Temperature - An increase in temperature
increases the rate of a reaction.
 Presence of a Catalyst (not all rxns have catalysts)
 A catalyst is a substance which increases the rate of a reaction
without being consumed in the overall reaction.
 The concentration of the catalyst or its surface area (if insoluble) are
variables which influence the rate.
 Some catalysts are incredibly complex - like enzymes; and others are
quite simple: H+ + H2O + CH2 = CH2 ------) CH3-CH2-OH + H+
 Type of Reactants
 “Surface Area of an Insoluble Reactant”
RAJVEER BHASKAR, RCPIPER

2. II. Rates
 Reaction Rate = either the increase in M of product per unit time
or the decrease in M of reactant per unit time; ΔM / ΔT
Note: [X] = moles X / Liter
 Example: H+ Catalyst
Sucrose + H2O --------------) Glucose + Fructose
Rate = rate of formation of either product.
Rate = Δ M of glucose / Δsec = Δ[glucose] / Δsec
or
Rate = rate of disappearance of either reactant.
Rate = - Δ[sucrose] / Δsec (- since want a + rate)
 In order to obtain rate, we need a way to measure ΔM of a
reactant or product with respect to time.

3. II. Rates
 Example: 2 N2O5 -----) 4 NO2 + 1 O2
If we want to equalize the rates then:
Rate = Δ[O2] = 1/4 Δ[NO2] = - 1/2 Δ[N2O5]
Δt Δt Δt
- divide by balancing coefficients when we equalize rates.
 Various Rates can be determined: 1) instantaneous rate at a
given time; 2) average rate over a long period of time; or 3) the
initial rate – rate at the beginning of the rxn; ie rate at t=0.0 (this
is used the most).
 On next slide the Δ[O2] versus time is plotted for a reaction.
Note: 1) how the rate changes with time & 2) that rate is the tangent
at a given point on the curve.

4. II. Rates
 Need to obtain the change in M of a given reagent per change in
time; could follow any parameter related to concentration.
 Examples of what one might follow to obtain rates:
- a change in pressure (if gas produced or consumed in the rxn)
- a change in pH (if acidity changes in the rxn)
- a change in absorbance of electromagnetic radiation (EMR)
Usually measure absorbance of Visible or UV EMR at a given λ - caused
by a change in reactant or product concentration.
A = Εbc at given λ (wavelength) This is Beer’s Law from Ch 121 (know)
A = absorbance; use spectrophotometer to measure; has no units.
Ε = molar absorptivity = a constant @ given λ; has units of M-1cm-1
b = pathlength of EMR through sample; usually 1.00 cm cuvette used.
c = concentration in M
 A plot of A versus M @ given λ will yield a straight line and the equation:
A = Ebc + intercept If follow ΔA then can convert to ΔM & get rate.

5. III. Rate Law: rate = k x [A]m x [B]n for A + B
 Rate Law relates the rate to temperature & concentration.
 Rate law is given in terms of REACTANTS only (convention).
 k = rate constant & handles the temperature variable.
 The exponents are the order & handle the concentration variables.
 General form of the rate law for: a A + b B c C + d D
rate = k x [A]m x [B]n
- Order for A is m & order for B is n; Overall order is: m + n
- m & n are determined experimentally.
- k, also determined experimentally & units depend upon overall order.

6. III. Rate Law - Rate Constant & Units
Note: Assume time is in seconds (s). Rate = k [A]x
Solve for k & plug in units; k = Rate / [A]x
(this may be useful for one of the online HW problems)
Overall Rxn Order, x Units for k
zero Ms-1
first s-1
second M-1s-1
third M-2s-1

7. IV. Order
 The concentration variables are handled by the exponents - the order.
 The orders are determined experimentally except for one case: An
elementary reaction.
 Elementary reactions are one step reactions which are the individual
steps in a mechanism. (For an elementary reaction only: the
balancing coefficients determine the order.) - Important
Example 1 for a multistep reaction: 1 CH2Br2 + 2 KI ---) 1 CH2I2 + 2 KBr
If experimentation found that m & n were both first order; then:
rate = k [CH2Br2 ]1 [KI]1
Example 2 for an elementary reaction: 2 O3 ---) 3 O2 (told it is elementary)
No need for experimentation; order comes from balancing coefficients:
rate = k[O3]2

8. IV. Determination of Order
 Order - from units of k: If you are given the units of the
rate constant for a reaction, then you will know the overall
order (slide 14). Not too common.
 Order by Method #1 - from altering M: Measure initial
rates keeping one reactant constant and change the
concentration of another; observe the rates; calculate order
as illustrated in the next few slides.
 Order by Method #2 - from integrated rate expression:
Use calculus & integrate the rate expression between the
limits of time = 0 & time = t. By plotting out the variables
of these integrated rate expressions you can determine the
order. This will be shown in the lecture, and you will be
doing this in the kinetics lab.

9. Order by Method #1 - from altering M:
Measure initial rates keeping one reactant
constant and change the concentration of
another; observe the rates; calculate order as
illustrated in the next few slides.

10. IV. Determination of Order by varying M
 Example #1: Determine the order for & rate expression for:
2N2O5 ---) 4NO2 + 1O2 rate = k [N2O5]m
Exp #1: Rate = 4.8x10-6 Ms-1 at 1.0x10-2 M N2O5
Exp #2: Rate = 9.6x10-6 Ms-1 at 2.0x10-2 M N2O5
Order: Note that when [N2O5] doubles, the rate doubles. Since
rate α [N2O5]m & rate doubles when [N2O5] doubles, the value of
must be 1; the order is 1.
- rate α [N2O5]m & rate doubles when [N2O5] doubles, then:
go from [1]m = 1 to [2]m = 2 m has to be 1
Rate law: rate = k x [N2O5]1

11. IV. Determination of Order by varying M
Summary
EFFECTS of doubling reagent M while keeping others constant:
Rate remains the same 0th order: [M]0
Rate doubles 1st order: [M]1
Rate quadruples 2nd order: [M]2
Rate increases eightfold 3rd order: [M]3

12. IV. Determination of Order by varying M
 Example #2: 2 NO + Cl2 -----) 2 NOCl - Calculate order of Rxn
Exp Initial [NO] Initial [Cl2] Initial Rate, Ms-1
1 0.0125 0.0255 2.27x10-5
2 0.0125 0.0510 4.57x10-5
3 0.0250 0.0255 9.08x10-5
Rate = k[NO]m[Cl2]n
a) calculate n: From 1 & 2 - double [Cl2] & keep [NO] constant
& rate increases by factor of 2.01; n = 1
b) calculate m: From 1 & 3 - double [NO] & keep [Cl2] constant
& rate increases by factor of 4.00; m = 2
Rate = k[NO]2[Cl2]1
2nd order wrt [NO]; 1st order wrt [Cl2]; 3rd order overall

13. Order by Method #2 - from integrated rate
expression:
 Integrate the rate expression between the limits of
time = 0 and time = t. By plotting out the variables of
these integrated rate expressions you can determine the
order. You will be doing this in the kinetics lab.

14. IV. Determination of Order by Integrated Rate Expression
 Summary on use of logarithms
 Log: involves #’s to the base 10; Log 10x = x
 Ln: Natural log uses #’s to the base e; Ln ex = x
 Ln [A/B] = Ln A - Ln B (or Log)
 Ln [A x B] = Ln A + Ln B (or Log)
 Ln Ab = b Ln A (or Log)
 To obtain either log or ln use the appropriate calculator function.
 Log 2.1x10-4 = - 3.68 (note significant figure change - see below)
(-4.0000000…. + 0.32 = -3.68 ; cut off at first doubtful digit)
 To remove Ln & Log use the inverse; ex & 10x functions on cal.
 Inverse [log 3.00] or 103.00 = 1.0 x 103
 Inverse [ln 3.00] or e3.00 = 20.

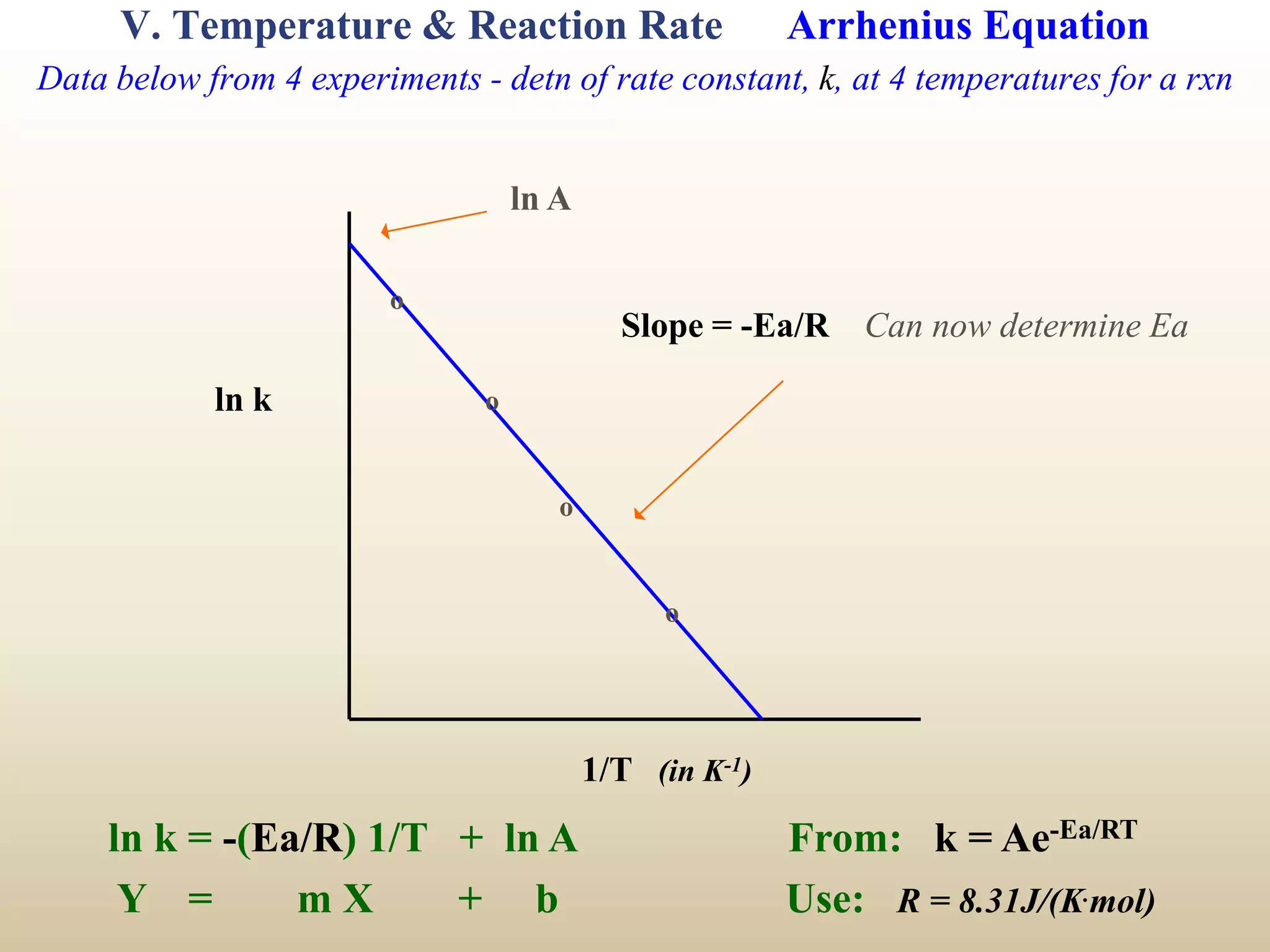
15. IV. Order Integrated Rate Law - First Order Rxns
1) 1st Order Reactions: aA -----) Products If 1st order, then
-Δ[A]/Δt = k[A]1 (rate expression)
- This plot for first order data only gives minimal information
[A]
Time

16. IV. Order Integrated Rate Law - First Order Rxns
1) 1st Order Reactions: aA -----) bB -Δ[A]/Δt = k[A]1
- if we integrate from time t to 0, we get the following:
Y = mX + b
ln[A]t = - kt + ln[A]o or ln{[A]t/[A]o} = -kt
where [A]t = M of A at time = t & [A]o = M of A at t = 0
- A plot of ln[A]t versus t gives a straight line (Y = mX +b):
b Slope (m) = - k
Note: Only linear for 1st order
ln[A]t
Time, t

17. IV. Order Integrated Rate Law - First Order Rxns
 Half-Life (t1/2) of 1st Order Reaction:
t1/2 = time it takes for [A]o to decrease to 1/2 initial M = ½[A]o
ln [A]t /[A]o = -kt ln 1/2[A]o /[A]o = -kt1/2
ln 1/2 = -kt1/2 -0.693 = -kt1/2 t1/2 = 0.693 / k
Note: 1) Time for 1/2 to disappear is independent of [A] for 1st order reaction.
2) This is an easy way to calculate 1st order rate constant, k.
Example: If t1/2 = 189 sec for 1st order decomposition of 1.0
mole of H2O2, then how much H2O2 will be left after 378 sec?
Note: 378/189 = 2 Goes through two half lives
1.0 mol ---) 0.50 mol ---) 0.25 mol

18. IV. Order Integrated Rate Law - Second Order Rxns
2) Second Order Reactions:
- Assume that aA -----) Products is 2nd order
Rate = - Δ[A] / Δ t = k [A]2
Integrate rate expression from time t to 0 & get following:
1/[A]t = k t + 1/[A]o So, a plot of 1/[A]t vs t should give a
straight line with slope = k and y intercept = 1/[A]o
t1/2 = 1 Note: Now t1/2 depends on initial M
k x [A]0
Note: can tell if reaction is 2nd order from 1/[A] vs t plot.

19. IV. Order Integrated Rate Law - Second Order Rxns Example
Plot of ln[NO2] vs t is not
linear – not 1st order.

20. IV. Order Integrated Rate Law - 0th Order
3) 0th Order Reactions Assume A ---) B is 0th order:
Rate = -k[A]0
Rate = -k
- “Integrated” Rate Equation for a 0th order reaction:
[A]t = -k x t + [A]0
- a plot of [A]t versus t will give a straight line
- Again, if you let [A]t = 1/2 [A]o then t = t1/2
- t1/2 = [A]0 / 2k

21. IV. Order Integrated Rate Law - Summary
Δ Rate
when
double [M]
None
Double
Quadruple

22. IV. Order Integrated Rate Law - Summary
[A]t
Time, t
ln[A]t
Time, t
1/[A]t
Time, t
0th Order n=0
[A]t = - kt + [A]o
1st Order n=1
ln[A]t = - kt + ln[A]o
2th Order n=2
1/[A]t = kt + 1/[A]o
A B Δ[A]/Δt = k[A]n
Note: slope = k in
each case

23. V. Temperature
 A collision needs to occur before a reaction can take place, &
the rate constant (& rate) of the reaction depends upon the:
1) collision frequency (temperature)
2) number of collisions having enough energy for rxn (Ea)
3) orientation of particles upon collision
 Ea = energy of activation = minimum energy of collision in
order for the reaction to take place.
 Ea & ΔH can be represented by Potential Energy Diagram;
can draw for one step or for several steps in a mechanism.

24. V. Temperature & Reaction Rate
A) Potential Energy Diagram for an Elementary Reaction
ΔH
(Exothermic)
What is Ea for reverse reaction?

25. V. Temperature & Reaction Rate Arrhenius Equation
 Arrhenius Equation relates: rate constant (k), temperature
(T), energy of activation (Ea in J/mole), & orientation factor.
k = A e-Ea/RT R = gas constant; use R = 8.31 J/(Kmole)
Take ln of both sides: ln k = -(Ea/R) 1/T + ln A
Y = m X + b
 Measure k at several temperatures and make plot of ln k
versus 1/T. Slope of the curve = - Ea/R (will give Ea)
 Note: A is a constant & includes orientation factor.
 Note: Page 559 contains a form of the Arrhenius equation
which may be useful for some online HW questions.

26. V. Temperature & Reaction Rate Arrhenius Equation
Data below from 4 experiments - detn of rate constant, k, at 4 temperatures for a rxn
ln k
1/T (in K-1)
ln k = -(Ea/R) 1/T + ln A From: k = Ae-Ea/RT
Y = m X + b Use: R = 8.31J/(K.mol)
Slope = -Ea/R Can now determine Ea
ln A
o
o
o
o

27. VI. Mechanisms A) Introduction
 Mechanism = step by step progress of chemical reaction.
 Most likely mechanism is determined experimentally from
a study of rate data.
 The mechanism consists of one or more elementary
reactions which add up to give you the overall reaction.
 Species which is generated & then consumed in the
mechanism is called an intermediate; Species which is
added, consumed & then regenerated is a catalyst.
 Step with largest Ea (slowest step) is called the rate
determining step & governs overall reaction rate.

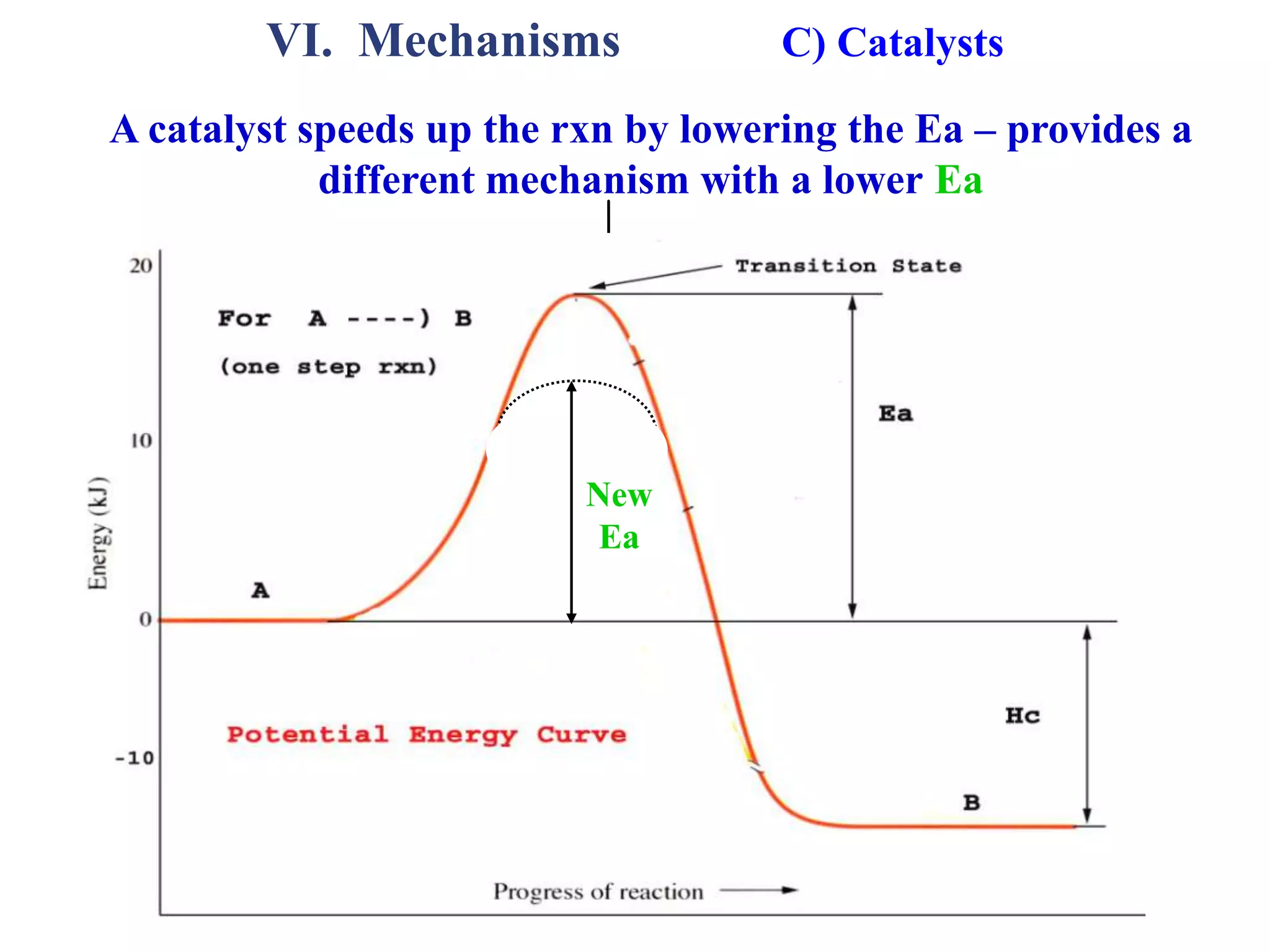
28. VI. Mechanisms B) Example 1 - Information
Overall Rxn: O3 + 2NO2 -----) O2 + N2O5
 Suggested two-step mechanism (from experimentation):
Step 1) O3 + NO2 -----) NO3 + O2 (slow)
Step 2) NO3 + NO2 -----) N2O5
rate = k [O3]1[NO2]1 - from slow first step
 Notes: a) Two elementary reactions (NOTE: balancing
coefficients = orders in an elementary rxn)
b) Steps add up to give overall rxn
c) NO3 is an intermediate (produced & used up)
d) There is no catalyst
e) Slowest step governs the overall rate
 mechanism is useful & will give us: a) practical data, b) rate
law, c) theoretical data, d) understanding of reaction

29. VI. Mechanisms B) Example 2 - Calculate Rate Expression
 Determine a) general rate expression & b) complete rate law from
the following mechanism Note: can directly get the order for an
elementary rxn from the balancing coefficients.
1) 1I2 2Io (fast equilibrium)
2) 2Io + 1H2 2HI (slow)
a) Overall Rxn from addn of steps: 1I2 + 1H2 2HI
General rate law: rate = k[I2]x[H2]y
b) Complete rate expression from mechanism:
From step #2: (rxn rate = slow step rate) rate = k2 [Io]2 x [H2]1
From step #1: Keq = [Io]2/[I2]1 [Io]2 = Keq[I2]1 Substitute into above:
rate = k2 Keq [I2]1 [H2]1
rate = k [I2]1 [H2]1

30. IV. Mechanisms C) Catalysts
 Catalyst = A chemical which speeds up a reaction without being
consumed in the reaction.
- They operate by lowering the Ea for the rate determining step.
- One example is Pt which speeds up the following rxn:
CO + 1/2 O2 -----) CO2
- Pt can be used in catalytic converter for your car exhaust.
 Most famous catalysts are proteins called enzymes.
- Enzymes = extremely specific biochemical catalysts that allow
complex reactions to take place in living systems under mild
conditions.
- Enzymes are very complex, well designed, and usually have
molecular weights in the tens of thousands.
- Their mode of operation uncovered only ~ 60 years ago.

31. VI. Mechanisms C) Catalysts
A catalyst speeds up the rxn by lowering the Ea – provides a
different mechanism with a lower Ea
New
Ea

32. VI. Mechanisms C) Catalysts