Chemical kinetics

Chemical Kinetics:
Rates and Mechanisms of
Chemical Reactions
C.P. Huang
University of Delaware
1

Content
1. Introduction
2. Reaction rate
3. Rate laws
4. Analysis of rate equations
5. Rate theories
6. Reaction mechanisms
1. Complex
2. Catalysis
3. Chain
7. Reactions in solution
8. Reactions at interface
2

• Chemical Kinetics: study of rates of chemical
reactions and mechanisms by which they occur
• A reaction may be spontaneous but does not occur at
measurable rates
Objectives
4

• How fast a reaction can take place?
• What steps or pathways are involved in any chemical
reaction?
• How complete is the chemical reaction?
• What are the two major factors controlling the
outcome of chemical reactions?
• Chemical thermodynamics
• Chemical kinetics
Why kinetics
5

Definition of reaction rate
• Rate – change in some variable per unit time
• Reaction rate – change in concentration per unit time;
M/s or mol/(L-s)
• Rates are determined by monitoring concentration as
a function of time
• Rates are negative for reactants and positive
quantities for products
7
Rate 1/time

Types of reaction rate
• Instantaneous rate – rate at a specific time
• Average rate – ∆[A] over a specific time interval
• Initial rate – instantaneous rate at t = 0
• Note: Rates and rate laws are not based on
stoichiometry!! They must be determined
experimentally.
8

• Kinetics are very difficult to describe from first
principles
– Structure, elements, behavior
• Rate of reaction describes how fast reactants are
used up and products are formed
• There are 4 basic factors that affect reaction rates
– Nature of reactants
– Effective concentrations
– Temperature
– Presence of catalysts
– Number of steps
Factors affecting reaction rate
9

Nature of reactants: particle size
• The degree of intimacy among particles obviously
depends on the physical nature of the particles.
• Particles in the liquid state are closer than in the
solid state.
• Likewise, particles in a finely divided solid will be
closer than in a chunk of the solid
• In both situations, there is a larger surface area
available for the reaction to take place
• This leads to an increase in rate.
The smaller the particles the faster the reaction rates
10

Nature of reactants: bonding
• Ions react rapidly:
Ag+ + Cl- AgCl(s) Very fast
• Reactions which involve bond breaking are slower:
NH4
+ + OCN- OC(NH2)2
• Redox reactions in solutions are slow
• Transfer of electrons are faster than those of atoms.
• Reactions between covalently bonded molecules are
slow:
2 HI(g) H2(g) + I2(g)
11


Concentration
• For every reaction the particles must come into
intimate contact with each other.
• High concentrations by definition implies that
particles are closer together (than dilute
solutions).
• So rate increases with concentration.
• Surface area
– larger surface area increases reaction
• Mixing increases interaction
• Need to minimized precipitation or colloid
formation
12

• Temperature affects rate by affecting the
number and energy of collisions
• So an increase in temperature will have the
effect of increasing reaction rate
Temperature
13

• Rate has units of moles per liter per unit time
- M s-1, M h-1
• Consider the hypothetical reaction
aA + bB  cC + dD
• We can write
Reaction rates and stoichiometry
14
t
D
dt
C
c
t
B
bt
A
a
r












][1][1
][1][1

15
Example
At a given time, the rate of C2H4 reaction is 0.23
M/s. What are the rates of the other reaction
components?
C2H4(g) + 3 O2(g) → 2 CO2(g) + 2 H2O(g)
0.23 M/s ? ? ?

Rate law
• Consider the following reaction
aA + bB  products
• Rate Law: equation describing the
relationship between the reaction rate and
concentration of a reactant or reactants
Rate = k[A]m[B]n
where k is called the rate constant
17

Concentration and rate
aA + bB → cC + dD
• General form of rate law:
rate = k[A]m[B]n
[A], [B] – concentration, in M or P
k – rate constant; units vary
m, n – reaction orders
• Reaction orders and, thus, rate laws must be
determined EXPERIMENTALLY!!!
– Note: m ≠ a and n ≠ b
– Overall order = sum of individual orders
18

Reaction order
• Rate = k[A][B]0 m = 1 and n = 0
- reaction is first order in A and zero order in B
- overall order = 1 + 0 = 1
- usually written: Rate = k[A]
• The values of the reaction order must be determined
experimentally; they cannot be found by looking at
the equation, i.e., the stoichiometry of the reaction
19

Rate law
• m, n are called reaction orders - they indicate the
sensitivity of the rate to concentration changes of
each reactant
• NOTE: the orders have nothing to do with the
stoichiometric coefficients in the balanced overall
equation
• An exponent of 0 means the reaction is zero order in
that reactant - rate does not depend on the
concentration of that reactant
20

Rate Law
• An exponent of 1, rate is directly proportional to the
concentration of that reactant
- if concentration is doubled, rate doubles
- reaction is first order in that reactant
• An exponent of 2, rate is proportional to the square
of concentration of that reactant
– if concentration is double, rate is quadrupled
– reaction is second order in that reactant
• The overall reaction order is the sum of all the orders
21

Reaction orders
For the reaction: A →B, the rate law is:
rate = k[A]m
Order (m) ∆[A] by a factor of Rate increases by
Zero (0) 2, 4, 15, ½, etc. None
1st (1)
2 2X
3 3X
2nd (2)
2 4X
3 9X
½ ¼X
22

Example
1. What is the order with respect to NO?
2. What is the order with respect to H2?
3. What is the overall order?
4. If [NO] is doubled, what is the effect on the reaction
rate?
5. If [H2] is halved, what is the effect on the reaction
rate?
6. What are the units of k?
23
2
1
3
quadrupled
halved
M-2-s-2
2 NO(g) + 2 H2(g) → N2(g) + 2 H2O(g)
rate = k[NO]2[H2]

24
Rate = 9x10-3 (h-1) x 0.02 (M) = 1.8x10-5 (M-h-1)
d[Cl]/dt = rate = 1.8x10-5 (M-h-1)
What is the rate of Cl- production under
these conditions?
Calculate the rate of reaction when the
concentration of PtCl2(NH3)2 is 2.0x10-2 M.
PtCl2(NH3)2 + H2O  PtCl(H2O)(NH3)2 + Cl-
Example

Calculate rate when [NO] = 0.025 M and [H2] = 0.015 M.
25
Rate = 6x10-4 (M-2-s-1)x0.025 M x 0.015 M
=225 (M-s-1)
2 NO(g) + 2 H2(g) → N2(g) + 2 H2O(g)
rate = k[NO]2[H2] k = 6.0 x 104 M-2s-1 @1000K
Example

Measurement of reaction rate
• Average reaction rate: a measure of the change in
concentration with time
• Instantaneous rate: rate of change of concentration
at any particular instant during the reaction
• Initial rate: instantaneous rate at t = 0; that is, when
the reactants are first mixed
26
Rate may be measured in three ways

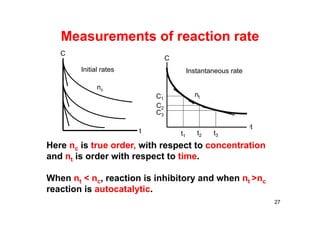
Measurements of reaction rate
Here nc is true order, with respect to concentration
and nt is order with respect to time.
When nt < nc, reaction is inhibitory and when nt >nc
reaction is autocatalytic.
27
Instantaneous rate
ntC1
C2
C3
t1 t2 t3
t
C
t
C
nc
Initial rates
nc
C
t

In this reaction, the
concentration of butyl
chloride, C4H9Cl, is
measured at various
times.
C4H9Cl(aq) + H2O(l) → C4H9OH(aq) + HCl(aq)
28
Time, s [C4H9Cl], M
0 0.1000
50 0.0905
100 0.0820
150 0.0741
200 0.0671
300 0.0549
400 0.0448
500 0.0368
800 0.0200
10,000 0

29
Time, s [C4H9Cl], M Average rate, M/s
0 0.1000
50 0.0905 1.9E-4
100 0.0820 1.7E-4
150 0.0741 1.6E-4
200 0.0671 1.4E-4
300 0.0549 1.22E-4
400 0.0448 1.01E-4
500 0.0368 0.8E-4
800 0.0200 0.56E-4
10,000 0

C4H9Cl(aq) + H2O(l) → C4H9OH(aq) + HCl(aq)
30
Initial rate
Instantaneous rate at 500 s

Determination of rate law
• Measuring the initial rates as a function of the initial
concentrations
• Avoids problems of reversible reactions
• Initially there are no products so they cannot affect
the measured rate
• This method is chosen to check the effect of a single
reactant on the rate
31
The method of initial rate

Atlas Reactors
33
http://www.syrris.com/batch-products/atlas-parallel-system

Stopped-Flow Technique
34
http://www.hi-techsci.com/techniques/stoppedflow

Temperature Jump
35

Quench-Flow Technique
36

Summary of Experimental Methods
37
Method Range of half-life, s
Conventional 102 – 108
Flow 10-3 - 102
Relaxation 10-10 -1
pressure jump 10-6 - 1
temperature jump 10-7 - 1
field pulse 10-10 – 10-3
shock tubes 10-9 – 10-3
Kinetic spectroscopy 10-15 – 10-10

Types of rate laws
39
• Differential rate law or rate law: Shows how the
reaction rate changes with concentration
• Integrated rate law: Shows how concentration
changes with time

First order
]A)[I,T(k
dt
]A[d
ν
R
A

1
t)I,T(k
o e]A[]A[ 

t
.
)I,T(k
]Alog[]Alog[ o
3032

1.0
0.1
0.01
0.001
1 2 3
t
Log [A]
40

Second order
2
A
]A)[T(k
dt
]A[d1
R 


t)T(kν
]A[]A[
i
0
11
41
  t)T(k]A[]B[
]A[
]B[
ln
]A[
]B[]A[
ln oAoB
o
oAoAoB





 





 

Third order
]C][B][A)[T(k
dt
]A[d1
R
A



1CBA 
ooo ]C[]B[]A[ 
t)T(k2
]A[
1
]A[
1
2
o
2

42

Summary Rate Equations
43
Rate = k[A]n; [A] = concentration at time t, [Ao] = initial concentration, [X] =
product conc.
[A0]-[A] = kt, [X] = kt
ln[A0] - ln[A] = kt, ln[A0] - ln([Ao] - [X]) = kt
0 order k = M/s
1st order k = 1/s
2nd order
k = M-1-s-1
3rd order k = M-2-s-1

Half-life
• The half-life, t1/2, is defined as the time it takes for
the reactant concentration to drop to half its
initial value
• Note: the half-life for a first order reaction does
not depend on the initial concentration
• The value of the half-life is constant
44

Half-Life
45
• Half-life
– A =Aoe-t
–  = ln2/t1/2
– If a rate half life is known,
fraction reacted or
remaining can be
calculated
(CH3)2N2(g)  N2(g) + C2H6(g)
Time Pressure (torr)
0 36.2
30 46.5
Ct =Coe-kt
kt0.5=ln(2)
to.5 = - [ln(2) t]/[ln(Ct/Co)]
to.5 = - [ln(2) (30)]/[ln(25.9/36.5)]=62.1 (min)
t A B C
0 36.2 0 0
3036.2(1-x) 36.2x 36.2x
46.5 = 36.2(1-x+2x)=36.2(1+x)=36.2+36.2x
46.5-36.2 = 36.2x x = 0.285
A = 36.5(1-0.285) = 25.9

46
t0.5
2t0.5
t0.53
t0.5 t0.5
t0.5

ARRHENIUS’ EQUATION
• In 1885, Hood proposed the following
equation:
• In 1884, vant’s Hoff-Arrhenius
proposed the following equation:
Kc is the equilibrium constant
T
A'
Blogk 
2
c
RT
E
dT
Klnd 

48

ARRHENIUS’ EQUATION
49
E1
E2
E=Ea
Initial state
Final state
Activated state; X*
E1
E2
E=Ea
Initial state
Final state
Activated state; X*
DCBA kk
 11
]][[]][[ 11 DCkBAk 
]][[
]][[
1
1
BA
DC
k
k
Kc 

11  EEE
2
11 lnln
RT
E
dt
kd
dt
kd 
 
1
ln
2
11

RT
E
dt
kd
1
ln
2
11
 
RT
E
dt
kd
2
ln
RT
E
dT
kd a

C
RT
E
k a
ln C = constant

Arrhenius Equation
• Svante Arrhenius developed an equation for the
mathematical relationship between k and Ea.
• A is the frequency factor, which represents the
number of effective collisions.
• : Boltzmann expression for the fraction of system
having energy in excess of the value, Ea, so that is
may be identified with the fraction of reactant
molecules that are activated complexes
50
RT
Ea
e


Arrhenius Equation
Y = m x + b
51
Or
log k = log A –Ea/(2.303 R) (1/T)
Slope = Ea/2.303 R = Ea/4.57 Cal

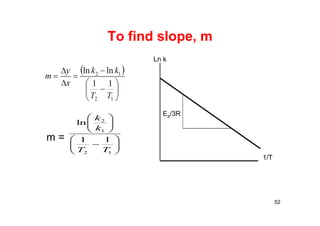
To find slope, m
52













12
1
2
11
ln
TT
k
k
m =
Ln k
1/T
Ea/3R

Arrhenius’ Equation
• This is Arrhenius’ Equation
• Can be arranged in the form of a straight line
• ln k = (-Ea/R)(1/T) + ln A
• Plot ln k vs. 1/T  slope = -Ea/R
1.0
0.1
0.01
0.001
1 2 3
1/T
Log [k]
EA/2.303
= dlog K/d(1/T)
Diffusion
regime
Reaction
regime
Ea < 5 kcal/mol: diffusion
control reaction
Ea > 5 kcal/mol; reactive
control
53

Activation Energy, Ea
• Energy barrier (hump) that must be overcome
for a chemical reaction to proceed
• Activated complex or transition state –
arrangement of atoms at the top of the barrier
54

Temperature Effects
• At higher temperatures, more molecules will have
adequate energy to react.
• This increases the reaction rate.
Maxwell-Boltzmann Distribution
55

Example
56
A reaction which rate constant doubles when
temperature is raised by 10oK from 300 oK. What is
its Ea value?
Given k310 = 2k300
or k1 = 2k0
Given k310 = 2k300
or k1 = 2k0
 
)mol/J(53594
k2
k
ln)34.8(
)310300(
300)(310
k
k
ln
TT
TT
E
o
o
1
0
1o
o1
a 





Summary of A and Ea
Reaction A Ea(kJ/mol)
N2ON2+O 8x1011 251 1st
N2O5 2NO+O2 6x1014 88 1st
N2+ON+NO 1x1011 315 2nd
OH+H22H2O+H 1x1011 42 2nd
CO2+OH-HCO3
- 1x1011 315 2nd
57

Example








12
a
1
2
1
a
1
T
1
T
1
R
E
k
k
ln
RT
E
Alnkln














1
2
12
21
a
k
k
lnR
TT
TT
E
)mol/kJ(8.57)mol/J(57811
00123.0
0394.0
)34.8(
298350
)298)(350(
Ea 













94.5578.070.8
298
1
308
1
324.8
57811
)00123.0ln(kln 






)ms/1(10x63.200263.0ek 394.5 

58
It is given for a specific reaction, k =0.00123 /ms at
290oK and 0.0394/ms at 350oK. What is its Ea and k
at 308oK?

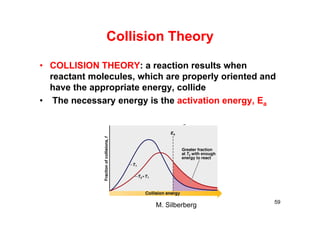
Collision Theory
• COLLISION THEORY: a reaction results when
reactant molecules, which are properly oriented and
have the appropriate energy, collide
• The necessary energy is the activation energy, Ea
M. Silberberg 59

Molecular Orientation and Effective
Collisions
• Not all collisions leads to a reaction
• For effective collisions proper
orientation of the molecules must be
possible
60

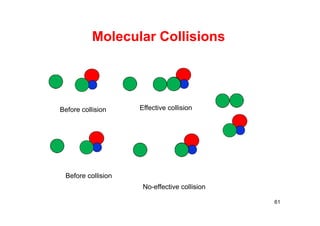
Molecular Collisions
61
Before collision Effective collision
Before collision
No-effective collision

Collision Theory
RT
E
AAezv


22
AA ncd2
2
1
z 
m
T
dn2
m
T8
nd2
2
1
z 2222
AA





RT
E
BA
BA2
ABBA e
mm
mm
T8dnnv
2
1






 
 62
molecules/(cm3-s)
mπ
Tκ
c
8
 = average velocity of each molecule
m: mass of each molecules
k = Boltzmann constant
dAB: average distance, sum of radii
two identical gas molecules colliding with each other at a velocity,
v (molecules/cm3-s) [N.C. Leuis (1918) and Eyring (1935)]
zAA = # collision/(s-cm3)

Collision Theory
RT
E
BA
BA2
AB
BA
e
mm
mm
T8d
nn
v
'k
2
1






 

RT
E
BA
BA2
ABa e
mm
mm
T8dNk
2
1






 

Z
mm
mm
T8dNA
2
1
BA
BA2
ABa 




 

RT
E
2
1
eBTk


T
Z
B 
RT
E
PZek


63
k = k’Na (cm3/mol-s)
RT
E
BA
BA2
ABBA e
mm
mm
T8dnnv
2
1






 


Example
64
Estimate he rate constant for the decomposition of HI(g)
molecules at 321.4oC according to the collision theory.
Given for the HI(g) molecules the following prosperities:
2HI(g) = H2(g) +I2(g)
= 3.5 Å = 3.5x10-8 cm;
E = 44,000 cal/g-mol;
mA = mB = MHI = 128 g;
R = Na = 1.38x10-16x6.023x1023
= 8.3x107 (erg/oK-mol) = 1.98 (cal/oK-g-mol)
T = 273 + 321.4 = 594.6 oK

Example
 
)smolecules/cm(10x72.9
e10x70.1
e
128
2
6.59410x3.88)10x5.3('k
327
4.3710
)6.594)(10x34.8(44000728 7
2
1


















65
k =9.72x10-27
(cm3/moleculesx)(6.023x1023)(molecules/mol)
= 5.86x10-3 (cm3/mol-s)
=5.86x10-3x(1000)
=5.85x10-6 (L/mol-s)

Example
Collision of two water molecules at room temperature, 298 oK,
given:
d = 0.30 nm, T=298oK;
mA=mB=18(g-mol-1)/6.023x1023 =2.99x10-26 kg;
 =1.38x10-23 J/oK
    
  
)smolecules/cm(10x37.2
)smolecules/m(10x37.2
10x6/10x99.2
29810x38.18
10x3.0Z
310
316
2
1
26226
23
29

















66

Example
Reaction k’
(cm3-molecules-1-s-1)
k
(L-mol-1-s-1)
CH4+OHCH3 + H2O 8.14x10-15 4.9x1012
CH3+O2 CH2O+OH 3.76x10-36 2.26x10-9
CH3O+O CH2O+OH 1.7x10-11 1.02x1016
67
k (L-mol-1-s-1) = 1000 x6.023x1023 k’ (cm3-molecules-1-s-1)

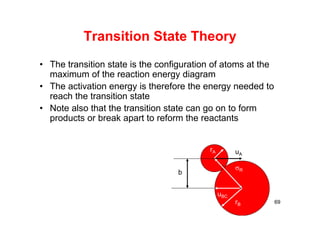
Transition State Theory
• During a chemical reaction, reactants do not suddenly
convert to products
• The formation of products is a continuous process of
bonding breaking and forming
• At some point, a transitional species is formed containing
“partial” bonds
• This species is called the transition state or activated
complex
68

• The transition state is the configuration of atoms at the
maximum of the reaction energy diagram
• The activation energy is therefore the energy needed to
reach the transition state
• Note also that the transition state can go on to form
products or break apart to reform the reactants
b
rA
rB
R
uBC
uA
69

]][[
*][**
*
BA
AB
aa
a
K
BA
AB
BA
AB



]][[*
*
BAKr
BA
AB



RT
G
eK
*
*



T
  = 6.624x10-27 erg/s
70

K = 1.38x10-16 erg/oK
A + B = AB*  C
r = [AB*];  (s-1); [AB*](molecules/cm3)

Transiton Theory
 RTHRS
BA
AB
e
T
r /*/*
*











 RS
BA
AB
e
T
A /*
*











 
   
RTH
RTHRS
RTHRS
BA
AB
TZe
eef
T
ee
T
r
/*
/*/*
/*/*
*


















E =H*
71

Summary of Rate Theory
RT
Ea
Aek

 RT
Ea
RT
E
2
1
eBTk


RT
Ea
RT
*H
R
*S
ee
T
k



R
*S
e
T 
 RT
*H
Rate Theory Equation A term Exponential
term
Arrhenius A
Collision BT1/2
Activated
Complex
(Transition)
72

Reaction Mechanisms
• Reactions occur in a series of elementary steps
collectively called a mechanism.
• Determining the reaction mechanism is the overall goal
of kinetic studies.
• One step, the rate-determining step (RDS), is much
slower than the other.
• Usually, an intermediate (isolable) or a transition state
(non-isolable) is formed at some point during the
reaction.
• molecularity – the number of molecules that participate
in a reaction
74

Reaction Mechanism
• MECHANISM: the step-by-step pathway by which a
reaction occurs
• Each step is called an elementary step
– NO2(g) + CO(g)  NO(g) + CO2(g)
• Mechanism:
– NO2(g) + NO2(g)  NO(g) + NO3(g)
– NO3(g) + CO(g)  NO2(g) + CO2(g)
• NO3 is a reaction intermediate
75

Reaction Mechanism
• The slow step is called the rate-
determining step (RDS) or rate-limiting
step (RLS)
• A reaction can never occur faster than its
slowest step
• Overall reaction = sum of all elementary
steps
• The mechanism proposed must be
consistent with the rate law
76

Elementary Steps and Molecularity
Molecularity is the number of molecules reacting.
77
Molecularity Elementary Reaction Rate Law
Unimolecular A  products Rate = k[A]
Bimolecular A + A  products Rate = k[A]2
Bimolecular A + B  products Rate = k[A][B]
Trimolecular A + A + A  products Rate = k[A]3
Trimolecular A + A +  products Rate = k[A]2[B]
Trimolecular A + B + C  products Rate = k[A][B][C]

Steady-state Approach
• When reaction mechanism has several steps of
comparable rates, the rate-limiting step is often not
obvious. There are intermediates in some steps.
• SSA: a method used to derive a rate law based on the
assumption that one intermediate is consumed as
quickly as it is generated.
78
2 N2O5  4NO2 + O2 N2O5  NO2 + NO3 (1)
NO3 + NO2  NO+ NO2 + O2 (2)
NO3 + NO  2NO (3)

79
2N2O5 4NO + O2
N2O5 NO2 + NO3
k1
k-1
NO3 + NO NO + NO2 + O2
k2
NO3 + NO 2NO
k3
0]][[]][[
][
3332  NONOkNONOk
dt
NOd
][
]][[
][
33
232
NOk
NONOk
NO 
0]][[]][[]][[][
][
32133232521
3
  NONOkNONOkNONOkONk
dt
NOd
]][[]][[]][[
][
][
32133232
521
3
NONOkNONOkNONOk
ONk
NO



80
])[2(
][
][])[(
][
][][][
][
][
212
521
2
3
2
3212
521
21322
521
3
NOkk
ONk
NO
k
k
kNOkk
ONk
NOkNOkNOk
ONk
NO















]['
)2(
][
])[2(
]][[
]][[
][
52
12
52321
212
252321
232
2
ONk
kk
ONkkk
NOkk
NOONkkk
NONOk
dt
Od
r









Catalysis
• Catalyst – increases the rate of a reaction without being
consumed or changing chemically
• Accomplishes this by lowering the activation energy by
changing the reaction mechanism.
• Heterogeneous vs. homogeneous catalysis
• Examples:
– Catalytic converter
– Enzymes in the body
– Ozone depletion
81

Catalysis
• Reaction rates are also affected by catalysts
• Catalyst: a substance that increases the rate
of a reaction without being consumed in the
reaction
• Catalysts work by providing alternative
pathways that have lower activation energies
• A catalyst may be homogeneous or
heterogeneous
• Homogeneous: catalyst and reactants are in
the same phase
82

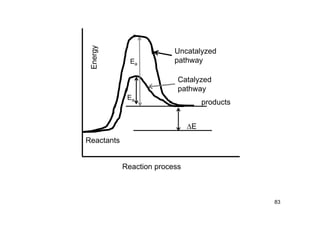
83
Energy
Reaction process
Uncatalyzed
pathway
Catalyzed
pathway
Reactants
products
E
Ea
Ea

• Heterogeneous: catalyst in a different phase
• Typically: a solid in a liquid
• An important example: catalytic converters in
automobile
- convert pollutants to CO2 H2O, O2, N2
- usually Pt, Pd, V2O5, Cr2O3, CuO
• Cars must use unleaded fuels – lead poisons the
catalytic bed
84

Enzyme Kinetics
Michaelis-Menten mechanism for enzyme kinetics is:
85

86
Catalytic efficiency, 
 = kcat/KM
 = k2/[(k-1+k2)/k1]
  max, = k1; if k2 >>k-1
k1 = rate of formation of ES
Diffusion limit ~ 108 – 109 M-1-s-1
For enzyme sized molecules at room
temperature
Decomposition of hydrogen peroxide
 = 4x108 M-1-s-1
Turnover number or catalytic constant
= number of catalytic cycles performed by the activate
Site in a given time intervals divided by the duration of that

87
Lineweaver Burk Plot ][
][max
SK
Sv
v
M 

   SSv
K
v
M 111
max

   
maxmax v
S
v
K
v
S M
   MM K
v
K
v
S
v
 max
1/vmax
KM/vmax
1/v
1/[S]
vmax/KM
1/KM
v/[S]
v
KM/vmax
1/vmax
[S]/v
[S]

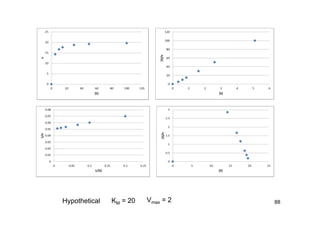
88Hypothetical KM = 20 Vmax = 2

89
Enzyme Inhibition
Reversible: enzyme activity can be regenerated by
removing the inhibitors.
Irreversible: complete loss of enzyme activity after
a period of time

90
Competitive Inhibition
0][][]][[
][
211   ESkESkSEk
dt
ESd
0][][]][[
][
433   EIkEIkIEk
dt
EId
  
  MK
k
kk
ES
SE


 
1
21
  
  IK
EI
IE

][][][ EIESEEo 
IM
o
K
IE
K
SE
EE
]][[]][[
][ 







IM
o
K
I
K
S
EE
][][
1][
IM
o
K
I
K
S
E
E
][][
1
][


E + S ES  E + P
k1
+
I
EI E + Q
k3
KI
k-1
k2
k-3

91
][
][
2 ESk
dt
Pd

MK
SE
k
dt
Pd ]][[][
2
][
][][
1
][ 2
S
K
I
K
S
E
K
k
dt
Pd
IM
o
M 









][
][
1
][][ 2
S
K
I
K
SEk
dt
Pd
v
I
M
o
oEkv 2max 
1/v
[S]
1/vmax
[I]








][
][
1
][max
S
K
I
K
Sv
v
I
M
][
1][
1
11
maxmax SK
I
v
K
vv I
M














I
M
K
I
v
K ][
1
max
Inhibitor is replaced
from the active sites
by substrate at high [S]

92
Non-competitive inhabitation
Inhibitor binds to some other binding sites;
Inhibitor combines with both free E and ES
2 possible mechanisms:
Ternary complex is a dead-end complex and does
not breakdown to yield products
Ternary complex breaks down at a slow rate than he
ES complex
E + S ES  E + P
KM
+
I
+
I
EI + S EIS  E + P
KM
KI KI

93
E + S ES  E + P
k1
+
I
+
I
EI + S EIS  E + P
k3
KI KI
k-1
k2
k-3
][2 ESkv 
MIIM
M
KK
SI
K
I
K
S
K
S
v
v
]][[][][
1
][
max 















IM
M
K
I
S
K
S
K
S
v
v
][
1][
][
1
][
max
Vmax=k2E0
1/v
1/[S]
1/vmax-app







M
M
K
S
K
][
1
Iapp Kv
I
vv maxmaxmax
][11


1/vmax-app
[I]
1/vmax
1/(vmaxKI)
Henri-Michaelis-Menton Eq

94
Uncompetitive inhibition
No binding site for inhibitor until substrate is bound to
the enzyme, so only ternary complex is possible

95
][2 ESkv 
MIM
M
KK
SI
K
S
K
S
v
v
]][[][
1
][
max 

 







I
M
K
I
vSv
K
v
][
1
1
][
11
maxmax
Vmax=k2E0
1/v
1/[S]
1/v’
[I]
E + S ES  E + P
KM
+
I
EIS  E + Q
KI
 







IK
I
v
][
1
1
max
maxv
KM
IK
I
vv
][1
'
1
max

1/vmax
1/KI
Uncompetitive Inhibition

96
PESnSE n
n
n
SE
ES
K
]][[
][

n
n
n
n
SEKE
SEK
ESE
ES
Y
]][[][
]][[
][][
][




n
SK
Y
Y
][
1


KSn
Y
Y
log]log[
1
log 






][2 ESkv 
][][ ESEEo 
n
o SEKEE ]][[][ 
n
o
SK
E
E
][1
][


n
no
SK
SKE
ES
][1
][
][


n
n
o
n
SK
SKEk
ESkv
][1
][
][ 2
2


maxmax ][
11
v
K
Svv n

Yield
Hill eq.
n: Hill coefficient

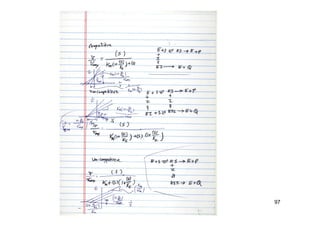
Chain Reactiosn
98
][
][
''1
]][['][
2
22
2
1
Br
HBr
k
BrHk
dt
HBrd


Chain reactions usually involve free radicals
The experimental rate law is
H2+Br2=2HBr

99
Initiation

 BrBrBr ak
2
Inhibition

 BrHHBrH dk
2
Termination 2BrBrBr ek
 
Propagation

 HHBrHBr bk
2

 BrHBrBrH ck
2

The Lindemann Mechanism
104
N2O5 = NO2 + NO3.
k1 >> k-2 [N2O5]
Rate  k2[N2O5]2
k1 << k-2 [N2O5]

7. Elementary Reaction in Solution
• Solvent effect
• Physical transfer
• Chemical effect
106

Reactions in Solution
• Upper limit for bimolecular steps of solution reaction.
Solutes behave like spheres undergoing Brown motion in
a viscous fluid and shows that the number of encounter
per cm3 per second is:
   111
4 BABABAE NNrrDDR  
dx
dN
DJ A
A
1

107

dr
dN
DrR A
AB
1
2
4
1
AN at r=(rA+rB) is 0
1
( 0)
1
2 4 A
rr
N
Ar
dr
B NdDR
BA
A
 


 
1
)(4 AABAB NDrrR  
   111
4 BABABAE NNrrDDR  
1000
))((4 BABAa
diff
rrDDN
k



L-mol-1-s-1
108
Total flux at r from B:

)(6 Tr
T
D



BA
BAa
diff
rrT
rrTN
k
)(3000
)(2 2

 

)(3000
8
T
RT
kdiff


)/(104.6
)01.0(3000
)298)(1031.8(8 8
7
smolLx
x
kdiff 
1)exp( 



diff
est
diff kk
Trr
ezz
BA
BA


)(
2


109

8. REACTION AT INTERFACES
• Mechanisms of surface reactions
• Transport from the bulk to the interface; AS
• Becomes adsorbed onto the surface: A+SAS
• Reacted at the surface: ASPS
• Desorbed from the surface: PS—P+S
• Transported back to the bulk:
P Bulk
110

Adsorption isotherms
(Langmuir)
11
1
BA
AS
NN
N
K 
1
AN = n/V =NaP/RT1
SN 1
TN=(1-)
1
ASN 1
TN= 
PN
T
K
a
1
1 



bP
bP


1

)(
1034.7 1
21

 atm
T
Kx
T
K
RT
KN
b a

111
K = RT/(1-)NaP
A+ S = AS; K
pV = nRT
n/V =P/RT

Adsorption Isotherm
(Fruendlich)
  

Pb
Pf
f
i
i
ii
1

f() = exp()
 = fraction of sites with energy of adsorption e between 0 and d.



 d
Pb
Pb





0
)(f(1
)(f(
Let Eads = 
T
PbT 
 )'(
m
aP
112

Maximum Adsorption Rate
112
2
1
1 8
SASE NN
T
R 









S
AS
AS
m
mm
mm



2222
SAS  
S = Total surface area of spheres in 1 cm3
12
)4( SS NrS 
= total number of spheres in 1 cm31
SN
1
2
1
1
2
A
A
S SN
m
T
R 








11
ASS SNkR 
2
1
2 






A
s
m
T
k


T
A
s pe
m
T
k 


 







2
1
2
113
A+SAS

Example
Calculate the rate constant for the adsorption of a
metal ion, with molecular weight of 100 g at room
temperature, 298 oK.
)/1)(/1)(/(1091.4
)/1)(/1)(/)(10023.6()10(1015.8
)(1015.8
1002
298104.1
2
22339
12139
2
1
16
12
scmmolLx
scmmolLxxxx
scmmoleculescmx
xx
xx
ks













114
2
1
2 






A
s
m
T
k



Langmuir-Hinshelwood
]][[
;
;
;
BSASkR
kSPBSAS
KBSSB
KASSA
s
s
B
A




2
)1( BBAA
BBAA
s
PbPb
PbPb
kR


A
B
s
AA
BB
s
AA
BBAA
s
P
P
k
Pb
Pb
k
Pb
PbPb
kR '
2
)(

2
)( BBAA
BBAA
s
PbPb
PbPb
kR


B
A
s
BB
AA
s
BB
BBAA
s
P
P
k
Pb
Pb
k
Pb
PbPb
kR '
)()( 2

BAs
BBAA
s PPk
PbPb
kR ,
1

115
bBPB <bAPA
bBPB > bAPA
bBPB , bAPA <1

Eley-Ridel Equation
skSCASB
KASSA
;
; 1


B
AA
AA
ss P
Pb
Pb
kASbkR


1
]][[
BsB
A
AA
sB
AA
AA
s PkP
P
Pb
kP
Pb
Pb
kR '
1



BAsBAAsB
AA
AB
s PPkPPbkP
Pb
Pb
kR '
1



116

Chemical kinetics

More Related Content

What's hot

Similar to Chemical kinetics

Recently uploaded

Chemical kinetics