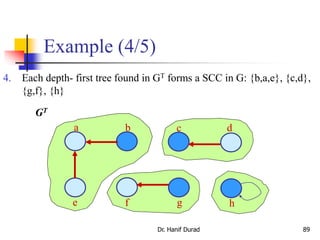
This document provides an outline and overview of a lecture on elementary graph algorithms. It begins with contact information for the lecturer, Dr. Muhammad Hanif Durad. It then outlines topics to be covered, including definition and representation of graphs, breadth-first search, depth-first search, topological sort, and strongly connected components. The document discusses the importance of graphs and examples of problems that can be modeled with graphs. It provides definitions and descriptions of basic graph terminology like vertices, edges, types of graphs. It also covers representations of graphs using adjacency lists and adjacency matrices. The document dives deeper into breadth-first search and depth-first search algorithms, providing pseudocode and examples. It discusses applications and analysis of the algorithms.

1. Chapter 23
Elementary Graph
Algorithms
Dr. Muhammad Hanif Durad
Department of Computer and Information Sciences
Pakistan Institute Engineering and Applied Sciences
hanif@pieas.edu.pk
Some slides have bee adapted with thanks from some other lectures
available on Internet. It made my life easier, thanks to Allah
Almighty .

2. Lecture Outline
 Definition and Representation
 Breadth-First Search
 Depth-First Search
 Topological Sort
 Strongly Connected Components (SCC)

3. Importance of Graphs
 Used to model a huge number of important (electrical
and computer) engineering problems
 General Scheduling and Allocation Problems
 relevant to parallel processing, manufacturing, etc…
 Design of Digital Systems (Synthesis, Verification and Test)
 from the physical level of abstraction to the system of abstraction
 Compilers
 All phases of compilation
 Analysis and Design of Communication Networks
 routing, bandwidth allocation, etc…
3
SL10.ppt

4. Graphs (1/2)
 Graph G = (V, E)
 V = set of vertices and E = set of edges
 Types of graphs
 Undirected: edge (u, v) = (v, u); for all v, (v, v)  E (No self
loops.)
 Directed: (u, v) is edge from u to v, denoted as u  v. Self loops
are allowed.
 Weighted: each edge has an associated weight, given by a weight
function w : E  R.
 Dense: |E|  |V|2.
 Sparse: |E| << |V|2
 |E| = O(|V|2)
19-graph1.ppt

5. Graphs (2/2)
 If (u, v)  E, then vertex v is adjacent to vertex u.
 Adjacency relationship is:
 Symmetric if G is undirected.
 Not necessarily so if G is directed.
 If G is connected:
 There is a path between every pair of vertices.
 Furthermore, if |E| = |V| – 1, then G is a tree.
 Other definitions in Appendix B (B.4 and B.5) as needed
|E|  |V| – 1 is wrong
MIT lectures

6. Representation of Graphs
 Two standard ways.
 Adjacency Lists.
 Adjacency Matrix
Dr. Hanif Durad 6
a
dc
b a
b
c
d
b
a
d
d c
c
a b
a c
a
dc
b
1 2
3 4
1 2 3 4
1 0 1 1 1
2 1 0 1 0
3 1 1 0 1
4 1 0 1 0

7. Adjacency Lists
 Consists of an array Adj of |V| lists.
 One list per vertex.
 For u  V, Adj[u] consists of all vertices adjacent to u.
a
dc
b a
b
c
d
b
c
d
d c
a
dc
b a
b
c
d
b
a
d
d c
c
a b
a c
If weighted, store weights also in
adjacency lists.

8. Storage Requirement
 For directed graphs:
 Sum of lengths of all adj. lists is
out-degree(v) = |E|
vV
 Total storage: (V+E)
 For undirected graphs:
 Sum of lengths of all adj. lists is
degree(v) = 2|E|
vV
 Total storage: (V+E)
No. of edges leaving v
No. of edges incident on v. Edge (u,v) is incident
on vertices u and v.

9. Pros and Cons: Adjacency Lists
 Pros
 Space-efficient, when a graph is sparse.
 Can be modified to support many graph variants.
 Cons
 Determining if an edge (u,v) G is not efficient.
 Have to search in u’s adjacency list. (degree(u)) time.
 (V) in the worst case.
Dr. Hanif Durad 9

10. Adjacency Matrix
 V|  |V| matrix A.
 Number vertices from 1 to |V| in some arbitrary manner.
 A is then given by:
a
dc
b
3 4
1 2 3 4
1 0 1 1 1
2 0 0 1 0
3 0 0 0 1
4 0 0 0 0
a
dc
b
1 2
3 4
1 2 3 4
1 0 1 1 1
2 1 0 1 0
3 1 1 0 1
4 1 0 1 0


 

otherwise0
),(if1
],[
Eji
ajiA ij
A = AT for undirected graphs.

11. Space and Time
 Space: (V2).
 Not memory efficient for large graphs.
 Time: to list all vertices adjacent to u: (V).
 Time: to determine if (u, v)  E: (1).
 Can store weights instead of bits for weighted graph.
Dr. Hanif Durad 11

12. Assignment 1
 Problems 22.1-1  22.1-3, 22.1-5 22.4-7,
page 530 531
 Last Date
 Tuesday -15 June 2010
Dr. Hanif Durad 12

13. Graph-searching Algorithms
 Searching a graph:
 Systematically follow the edges of a graph to visit the vertices
of the graph.
 Used to discover the structure of a graph.
 Efficiency and correctness
 Efficiency: Don’t loop or visit vertices repeatedly.
 Correctness: Don’t miss any vertex.
Dr. Hanif Durad 13
Ref: lecture11_elementary_graph_algorithms.pdf

14. Order of searching
 The order in which we search vertices depends
on the container used for storing discovered but
not finished vertices.
 There are two types of containers used:
 Queue: leads to so called breadth-first search.
 Stack: leads to so called depth-first search.
 We will investigate these two graph searching
algorithms in more detail
Dr. Hanif Durad 14
Ref: lecture11_elementary_graph_algorithms.pdf

15. 22.2 Breadth-First
Search (BFS)
Dr. Hanif Durad 15

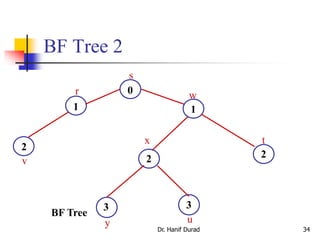
16. Breadth-First Search (BFS)
 Input: Graph G = (V, E), either directed or undirected,
and source vertex s  V.
 Output:
 d[v] = distance (smallest # of edges, or shortest path) from s
to v, for all v  V. d[v] =  if v is not reachable from s.
 [v] = u such that (u, v) is last edge on “shortest path” from s
to v.
 u is v’s predecessor.
 Builds breadth-first tree with root s that contains all reachable
vertices.
16
19-graph1.ppt
Shortest Path- path containing smallest no. of edges

17. Data Structure for BFS
 Expands the frontier between discovered and undiscovered
vertices uniformly across the breadth of the frontier.
 A vertex is “discovered” the first time it is encountered during the
search.
 A vertex is “finished” if all vertices adjacent to it have been
discovered.
 Colors the vertices to keep track of progress.
 White – Undiscovered.
 Gray – Discovered but not finished.
 Black – Finished.
 Colors are required only to reason about the algorithm. Can be implemented
without colors.
19-graph1.ppt

18. BFS for Shortest Paths
Dr. Hanif Durad 18
FinishedDiscoveredUndiscovered
S
11
1
S2
2
2
2
2
2
S
3
3 3
3
3

19. 19
BFS(G,s)
1. for each vertex u in V[G] – {s}
2 do color[u]  white
3 d[u]  
4 [u]  nil
5 color[s]  gray
6 d[s]  0
7 [s]  nil
8 Q  
9 enqueue(Q,s)
10 while Q  
11 do u  dequeue(Q)
12 for each v in Adj[u]
13 do if color[v] = white
14 then color[v]  gray
15 d[v]  d[u] + 1
16 [v]  u
17 enqueue(Q,v)
18 color[u]  black
white: undiscovered
gray: discovered
black: finished
Q: a queue of discovered
vertices
color[v]: color of v
d[v]: distance from s to v
[u]: predecessor of v
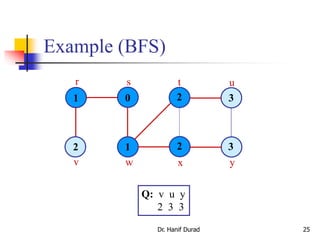
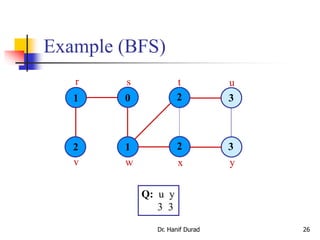
Example: animation.
Initialization
Set up s and initialize Q
Explore all the vertices
adjacent to u and update
d,  and Q

20. Example (BFS)
 0
  
 

r s t u
v w x y
Q: s
0
(Courtesy of Prof. Jim Anderson)
Dr. Hanif Durad 20

21. Example (BFS)
1 0
1  
 

r s t u
v w x y
Q: w r
1 1
Dr. Hanif Durad 21

22. Example (BFS)
1 0
1 2 
2 

r s t u
v w x y
Q: r t x
1 2 2
Dr. Hanif Durad 22

23. Example (BFS)
1 0
1 2 
2 
2
r s t u
v w x y
Q: t x v
2 2 2
Dr. Hanif Durad 23

24. Example (BFS)
1 0
1 2 
2 3
2
r s t u
v w x y
Q: x v u
2 2 3
Dr. Hanif Durad 24

25. Example (BFS)
1 0
1 2 3
2 3
2
r s t u
v w x y
Q: v u y
2 3 3
Dr. Hanif Durad 25

26. Example (BFS)
1 0
1 2 3
2 3
2
r s t u
v w x y
Q: u y
3 3
Dr. Hanif Durad 26

27. Example (BFS)
1 0
1 2 3
2 3
2
r s t u
v w x y
Q: y
3
Dr. Hanif Durad 27

28. Example (BFS)
1 0
1 2 3
2 3
2
r s t u
v w x y
Q: 
Output=?
Dr. Hanif Durad 28

29. Analysis of BFS (1/2)
 Initialization takes O(V).
 Outer loop (while):
 Can we bound the time until Q becomes empty?
 Only white vertices are enqueued, and they are
always grayed when enqueued
 Thus a vertex can be enqueued at most once
 One vertex dequeued for every lap
 Thus outer while loop executed O(|V|) times
29Dr. Hanif Durad

30. Analysis of BFS (2/2)
 Inner loop (for):
 The adjacency list of a vertex is scanned at most once,
and each element in the list is accessed only once
 Thus, the total time in inner loop is proportional
to sum of lengths of all adjacency lists O(|E|)
 Whole loop nest  O(|V|) + O(|E|) = O(|V| + |E|)
 Correctness Proof
 Self Study
30Dr. Hanif Durad
O(|V| + |E|)≠O (|EV|)

31. Print out the vertices on a shortest
path from s to v
Dr. Hanif Durad 31

32. PRINT-PATH Illustration
Dr. Hanif Durad 32
(1) PRINT-PATH(G, s, y)
(2) PRINT-PATH(G, s, x)
y
(3) PRINT-PATH(G, s, w)
x
y
(4) PRINT-PATH(G, s, s)
w
x
y
(5) s
w
x
y

33. BF Tree 1
3
y
1
r 0
s
2
t
3
u
2
v 2
x
BF Tree
1
w
Unique ?
Predecessor Subgraph

34. BF Tree 2
1
r 0
s
2
t
2
v 2
x
BF Tree
1
w
3
y
3
u
Dr. Hanif Durad 34

35. BF Tree 3
3
y
1
r 0
s
2
t
3
u
2
v 2
x
BF Tree
1
w
Dr. Hanif Durad 35

36. Application of BFS
 One application concerns how to find
connected components in a graph
 If a graph has more than one connected
components, BFS builds a BFS-forest (not just
BFS-tree)!
 Each tree in the forest is a connected component.
Dr. Hanif Durad 36
bfs2.ppt

37. BFS-forest
 Tree
 connected graph
without cycles
 Forest
 collection of trees
22_Graph.pdf
Dr. Hanif Durad 37

38. Assignment 2
 Problems 22.2-1, 22.2-3 22.4-8, Page 538
539
 C++ coding for BFS problem
 Last Date
 Tuesday -15 June 2010
Dr. Hanif Durad 38

39. 22.3 Depth-First
Search (DFS)
Dr. Hanif Durad 39

40. Depth-first Search (DFS)
 Explore edges out of the most recently discovered vertex v.
 When all edges of v have been explored, “backtrack” to
explore other edges leaving the vertex from which v was
discovered (its predecessor).
 “Search as deep as possible first.”
 Continue until all vertices reachable from the original
source are discovered.
 If any undiscovered vertices remain, then one of them is
chosen as a new source and search is repeated from that
source.
19-graph1.ppt
Dr. Hanif Durad 40

41. Data Structure for DFS
 Adjacency list
 color[u] for each vertex
 WHITE if u has not been discovered
 GRAY if u is discovered but not finished
 BLACK if u is finished
 Timestamps: 1  d[u] < f[u]  2|V|
 d[u] records when u is first discovered (and grayed)
 f[u] records when the search finishes examining u’s
adjacency list (and blacken u)
 [u] for predecessor of u
unit14.ppt

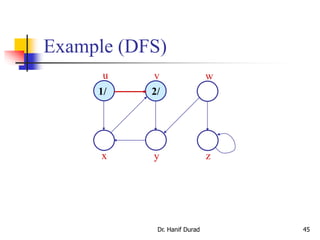
42. Depth-first Search (DFS)
 Input: G = (V, E), directed or undirected. No source
vertex given!
 Output:
 2 timestamps on each vertex. Integers between 1 and
2|V|.
 d[v] = discovery time (v turns from white to gray)
 f [v] = finishing time (v turns from gray to black)
 [v] : predecessor of v = u, such that v was discovered
during the scan of u’s adjacency list.
 Uses the same coloring scheme for vertices as BFS.
19-graph1.ppt

43. Pseudo-code
DFS(G)
1. for each vertex u  V[G]
2. do color[u]  white
3. [u]  NIL
4. time  0
5. for each vertex u  V[G]
6. do if color[u] = white
7. then DFS-Visit(u)
Uses a global timestamp time.
DFS-Visit(u)
1. color[u]  GRAY  White vertex u
has been discovered
2. time  time + 1
3. d[u]  time
4. for each v  Adj[u]
5. do if color[v] = WHITE
6. then [v]  u
7. DFS-Visit(v)
8. color[u]  BLACK  Blacken u;
it is finished.
9. f[u]  time  time + 1
Example: animation.
43
Init all
vertices
Visit all
children
recursively
Dr. Hanif Durad

44. Example (DFS)
1/
u v w
x y z
(Courtesy of Prof. Jim Anderson)
Dr. Hanif Durad 44

45. Example (DFS)
1/ 2/
u v w
x y z
Dr. Hanif Durad 45

46. Example (DFS)
1/
3/
2/
u v w
x y z
Dr. Hanif Durad 46

47. Example (DFS)
1/
4/ 3/
2/
u v w
x y z
Dr. Hanif Durad 47

48. Example (DFS)
1/
4/ 3/
2/
u v w
x y z
B
Dr. Hanif Durad 48

49. Example (DFS)
1/
4/5 3/
2/
u v w
x y z
B
Dr. Hanif Durad 49

50. Example (DFS)
1/
4/5 3/6
2/
u v w
x y z
B
Dr. Hanif Durad 50

51. Example (DFS)
1/
4/5 3/6
2/7
u v w
x y z
B
Dr. Hanif Durad 51

52. Example (DFS)
1/
4/5 3/6
2/7
u v w
x y z
BF
Dr. Hanif Durad 52

53. Example (DFS)
1/8
4/5 3/6
2/7
u v w
x y z
BF
Dr. Hanif Durad 53

54. Example (DFS)
1/8
4/5 3/6
2/7 9/
u v w
x y z
BF
Dr. Hanif Durad 54

55. Example (DFS)
1/8
4/5 3/6
2/7 9/
u v w
x y z
BF C
Dr. Hanif Durad 55

56. Example (DFS)
1/8
4/5 3/6 10/
2/7 9/
u v w
x y z
BF C
Dr. Hanif Durad 56

57. Example (DFS)
1/8
4/5 3/6 10/
2/7 9/
u v w
x y z
BF C
B
Dr. Hanif Durad 57

58. Example (DFS)
1/8
4/5 3/6 10/11
2/7 9/
u v w
x y z
BF C
B
Dr. Hanif Durad 58

59. Example (DFS)
1/8
4/5 3/6 10/11
2/7 9/12
u v w
x y z
BF C
B
Dr. Hanif Durad 59

60. Analysis of DFS
 Loops on lines 1-2 & 5-7 take (V) time,
excluding time to execute DFS-Visit.
 DFS-Visit is called once for each white vertex vV
when it’s painted gray the first time. Lines 3-6 of
DFS-Visit is executed |Adj[v]| times. The total
cost of executing DFS-Visit is vV|Adj[v]| = (E)
 Total running time of DFS is (V+E).
Dr. Hanif Durad 60

61. Output
 Tree or forest ?
 Is there any other forest possibility ?
1/8
4/5 3/6 10/11
2/7 9/12
x y z
BF C
B
Forest
Yes
 May depend upon order
 examined in line 5 of DFS,
 order in which the neighbors visited in line 4 of
DFS-VISIT.
 Don’t to cause problems in practice result
with essentially equivalent results
IA, P-542

62. Depth-First Trees
 Predecessor subgraph defined slightly different from
that of BFS.
 The predecessor subgraph of DFS is G = (V, E) where
E ={([v],v) : v  V and [v]  NIL}.
 How does it differ from that of BFS?
 The predecessor subgraph G forms a depth-first forest
composed of several depth-first trees. The edges in E are
called tree edges.
Dr. Hanif Durad 62
Definition:
Forest: An acyclic graph G that may be disconnected.

63. DFS on Undirected Graphs
 DFS on an undirected graph is complicated by the fact
that edges should be explored in one direction only,
 but they are represented twice in the data structure
(symmetric digraph equivalence)
 Depth-first search provides an orientation for each of its
edges
 they are oriented in the direction in which they are first
encountered (during exploring)
 the reverse direction is then ignored.
Dr. Hanif Durad 63
Modify Algo ?
CH07.ppt, P 32/36

64. Theorem 22.7
For all u, v, exactly one of the following holds:
1. d[u] < f [u] < d[v] < f [v] or d[v] < f [v] < d[u] < f [u] and neither
u nor v is a descendant of the other.
2. d[u] < d[v] < f [v] < f [u] and v is a descendant of u.
3. d[v] < d[u] < f [u] < f [v] and u is a descendant of v.
 So d[u] < d[v] < f [u] < f [v] cannot happen.
 Like parentheses:
 OK: ( ) [ ] ( [ ] ) [ ( ) ]
 Not OK: ( [ ) ] [ ( ] )
Corollary
v is a proper descendant of u if and only if d[u] < d[v] < f [v] < f [u].
Parenthesis Theorem
19-graph1.ppt

65. Dr. Hanif Durad 65
Relation to Stack ?
Stack Stack

66. White-path Theorem
Dr. Hanif Durad 66
Theorem 22.9
The white path property states that v is a descendant of u if
and only if, at the time of discovery of u, there is a white path
from u to v.
http://www.cs.mcgill.ca/~cs251/OldCourses/1997/topic26/
 Proof
 Self Study

67. Classification of Edges
 Tree edge: in the depth-first forest. Found by
exploring (u, v).
 Back edge: (u, v), where u is a descendant of v (in
the depth-first tree).
 Forward edge: (u, v), where v is a descendant of
u, but not a tree edge.
 Cross edge: any other edge. Can go between
vertices in same depth-first tree or in different
depth-first trees.
Dr. Hanif Durad 67

68. Classification of Edges
Dr. Hanif Durad 68
1/8
4/5 3/6 10/11
2/7 9/12
x y z
BF C
B
Tree edges Back edges Forward edges Cross edges

69. DFS of an Undirected Graph
Dr. Hanif Durad 69
Theorem:
In DFS of an undirected graph, we get only tree and back edges.
No forward or cross edges.
 Proof
 Self Study
1/8
4/5 3/6 10/11
2/7 9/12
x y z
BF C
B
Is it ok ?

70. Assignment 3
 Problems 22.3-1, 22.3-4, 22.3-7, 22.3-9 
22.3-12, Page 547 549
 C++ coding for DFS problem
 Last Date
 Tuesday -22 June 2010
Dr. Hanif Durad 70

71. Applications of
Depth-First
Search
Dr. Hanif Durad 71

72. 22.4 Topological
Sort
Dr. Hanif Durad 72

73. Directed Acyclic Graph (DAG)
 A directed path is a sequence of vertices
(v0, v1, . . . , vk)
 Such that (vi, vi+1) is an arc
 A directed cycle is a directed path such that the
first and last vertices are the same.
 A directed graph is acyclic if it does not contain
any directed cycles
Dr. Hanif Durad 73
connectivity-directed_graph.ppt

74. Topological Sort
 A topological sort of a DAG is a linear order of all
its vertices such that if G contains an edge (u, v),
then u appears before v in the ordering
 If the graph is not acyclic, then no linear ordering is
possible.
 A topological sort can be viewed as an ordering of its
vertices along a horizontal line so that all directed edges
go from left to right
 DAG are used in many applications to indicate
precedence among events
unit14.ppt

75. Topological Sort
Dr. Hanif Durad 75
Topological-Sort (G)
1. call DFS(G) to compute finishing times f [v] for all v  V
2. as each vertex is finished, insert it onto the front of a linked
list
3. return the linked list of vertices
Time: (V + E).
20-graph2.ppt

76. Characterizing a DAG (1/2)
Proof: : Show that back edge  cycle.
 Suppose there is a back edge (u, v). Then v is ancestor of
u in depth-first forest.
 Therefore, there is a path from v u, so v u v is
a cycle.
76
Lemma 22.11
A directed graph G is acyclic iff a DFS of G yields no back edges.
v u
T T T
B
20-graph2.ppt

77. Characterizing a DAG (2/2)
 Proof (Contd.):  : Show that a cycle implies a back edge.
 c : cycle in G, v : first vertex discovered in c, (u, v) : preceding
edge in c.
 At time d[v], vertices of c form a white path v u. Why?
 By white-path theorem, u is a descendent of v in depth-first forest.
 Therefore, (u, v) is a back edge.
77
Lemma 22.11
A directed graph G is acyclic iff a DFS of G yields no back edges.
v u
T T T
B
20-graph2.ppt

78. 78
unit14.ppt

79. Theorem 22.12
• TOPOLOGICAL-SORT(G) produces a
topological sort of a directed acyclic graph G
– Suppose that DFS is run on a given DAG G to determine
finishing times for its vertices. It suffices to show that for
any pair of distinct vertices u, v, if there is an edge in G
from u to v, then f[v] < f[u].
• The linear ordering is corresponding to finishing time ordering
– Consider any edge (u, v) explored by DFS(G). When this
edge is explored, v cannot be gray (otherwise, (u, v) will be
a back edge). Therefore v must be either white or black
• If v is white, v becomes a descendant of u, f[v] <f[u] (ex. pants &
shoes)
• If v is black, it has already been finished, so that f[v] has already
been set  f[v] < f[u] (ex. belt & jacket)
Dr. Hanif Durad 79
Self Study

80. Assignment 4
 Problems 22.4-1 22.4-5, Page 551 552
 C++ coding for Topological Sort
 Last Date
 Tuesday -22 June 2010
Dr. Hanif Durad 80

81. Strongly Connected Components
 G is strongly connected if every pair (u, v) of vertices in
G is reachable from one another.
 A strongly connected component (SCC) of G is a
maximal set of vertices C  V such that for all u, v  C,
both u v and v u exist.
20-graph2.ppt

82. Component Graph
 GSCC = (VSCC, ESCC).
 VSCC has one vertex for each SCC in G.
 ESCC has an edge if there’s an edge between the
corresponding SCC’s in G.
 GSCC for the example considered:
Dr. Hanif Durad 82
20-graph2.ppt
fig.from -lecture25.pdf

83. GSCC is a DAG
Dr. Hanif Durad 83
Lemma 22.13
Let C and C be distinct SCC’s in G, let u, v  C, u, v  C, and
suppose there is a path u u in G. Then there cannot also be a path
v v in G.
Proof:
 Suppose there is a path v v in G.
 Then there are paths u u v and v v u in G.
 Therefore, u and v are reachable from each other, so
they are not in separate SCC’s.
20-graph2.ppt

84. Transpose of a Directed Graph
 GT = transpose of directed G.
 GT = (V, ET), ET = {(u, v) : (v, u)  E}.
 GT is G with all edges reversed.
 Can create GT in Θ(V + E) time if using adjacency
lists.
 G and GT have the same SCC’s. (u and v are
reachable from each other in G if and only if
reachable from each other in GT.)
Dr. Hanif Durad 84
20-graph2.ppt

85. Algorithm to determine SCCs
Dr. Hanif Durad 85
SCC(G)
1. call DFS(G) to compute finishing times f [u] for all u
2. compute GT
3. call DFS(GT), but in the main loop, consider vertices in order of
decreasing f [u] (as computed in first DFS)
4. output the vertices in each tree of the depth-first forest formed in
second DFS as a separate SCC
Time: (V + E).
20-graph2.ppt

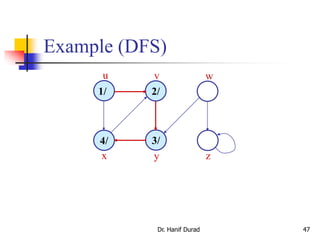
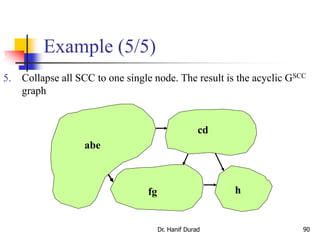
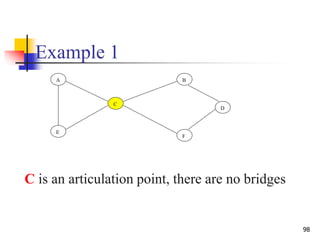
86. Example (1/5)
Dr. Hanif Durad 86
(Courtesy of Prof. Jim Anderson)
13/14
12/15 3/4 2/7
11/16 1/10
a b c
e f g
5/6
8/9
h
d
G
Sort nodes on their finishing time:
b,e,a,c,d,g,f,h
1. call DFS(G) to compute finishing times f [u] for all u
20-graph2.ppt
text taken from: lecture11_elementary_graph_algorithms.pdf

87. Example (2/5)
Dr. Hanif Durad 87
a b c
e f g h
d
GT
2. compute GT

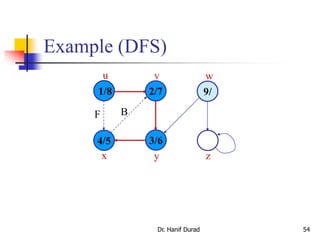
88. Example (3/5)
Dr. Hanif Durad 88
(Courtesy of Prof. Jim Anderson)
Deep- first- trees found: {b,a,e}, {c,d}, {g,f}, {h}
3. call DFS(GT), but in the main loop, consider vertices in order of
decreasing f [u] (as computed in line 1  b,e,a,c,d,g,f,h)
a b c
e f g h
d
GT

89. Example (4/5)
Dr. Hanif Durad 89
4. Each depth- first tree found in GT forms a SCC in G: {b,a,e}, {c,d},
{g,f}, {h}
a b c
e f g h
d
GT

90. Example (5/5)
Dr. Hanif Durad 90
cd
hfg
abe
5. Collapse all SCC to one single node. The result is the acyclic GSCC
graph

91. Analysis of SCC algorithm
1. Call DFS(G) to compute finishing times f[u] for each
vertex u in G Θ(V + E)
2. Compute transpose graph GT  Θ(V + E)
3. Call DFS(GT), but in he main loop, consider the
vertices in decreasing f[u] (as computed in line 1)
 Θ(V + E)
4. Collapse each depth-first tree found in GT to a SCC
 Θ(V + E)
Overall total time: Θ(V + E)
Dr. Hanif Durad 91

92. Assignment 5
 Section Problems 22.5-1, 22.5-3, 22.5-5
22.5-6, Page 557
 Chapter Problems 22-122-4 Page 558 560
 C++ coding for SCC
 Last Date
 Tuesday -22 June 2010
Dr. Hanif Durad 92

93. Graph Connectivity
 Connectivity
 Biconnectivity
 Articulation Points and Bridges
 Connectivity in Directed Graphs
Dr. Hanif Durad 93
L25-Connectivity.ppt

94. Connectivity
 Definition:
 An undirected graph is said to be connected if for
any pair of nodes of the graph, the two nodes are
reachable from one another (i.e. there is a path
between them).
 If starting from any vertex we can visit all other
vertices, then the graph is connected
Dr. Hanif Durad 94

95. Biconnectivity
Dr. Hanif Durad 95
A graph is biconnected, if there are no vertices
whose removal will disconnect the graph.
A B
C
D
E
A B
C
D
E
biconnected not biconnected

96. Articulation Points
Dr. Hanif Durad 96
Definition: A vertex whose removal makes the
graph disconnected is called an articulation
point or cut-vertex
A B
C
D
E
C is an articulation point
We can compute articulation points
using depth-first search and a special
numbering of the vertices in the order
of their visiting.

97. Bridges
Dr. Hanif Durad 97
Definition:
An edge in a graph is called a bridge, if its removal
disconnects the graph.
Any edge in a graph, that does not lie on a cycle, is a bridge.
Obviously, a bridge has at least one articulation point at its end,
however an articulation point is not necessarily linked in a bridge.
A B
C
D
E
(C,D) and (E,D) are bridges

98. 98
Example 1
A B
C
E
F
D
C is an articulation point, there are no bridges

99. 99
Example 2
A B
C
E
F
D
C is an articulation point, CB is a bridge

100. 100
Example 3
A
B
C
E
F
G
D
B and C are articulation points, BC is a bridge

101. 101
Example 4
A
B C D
E
B and C are articulation points. All edges are bridges

102. 102
Example 5
A
B
C
D E
F
G
Biconnected graph - no articulation points and no
bridges

103. 103
Connectivity in Directed Graphs (I)
Definition: A directed graph is said to be strongly
connected if for any pair of nodes there is a path
from each one to the other
A B
C
D
E

104. 104
Connectivity in Directed Graphs
(II)
Definition: A directed graph is said to be
unilaterally connected if for any pair of nodes at
least one of the nodes is reachable from the other
A B
C
D
E
Each strongly
connected graph is
also unilaterally
connected.

105. 105
Connectivity in Directed Graphs
(III)
Definition: A directed graph is said to be weakly
connected if the underlying undirected graph is
connected
A B
C
D
E
There is no path
between B and D
Each unilaterally
connected graph is
also weakly connected

106. Self Study Articles
 Articulation Points and Bridges
 Bi-connected Component
 Algorithm to Articulation Points in a Graph
 Euler Tour
 Reachability
Dr. Hanif Durad 106
Are Related Chapter Problems 22-122-4
Page 558 560

107. Self Study Slides
from here onward
Dr. Hanif Durad 107

108. How does it work? (1/2)
 Idea:
 By considering vertices in second DFS in decreasing
order of finishing times from first DFS, we are
visiting vertices of the component graph in
topologically sorted order.
 Because we are running DFS on GT, we will not be
visiting any v from a u, where v and u are in different
components.
Dr. Hanif Durad 108

109. How does it work? (2/2)
 Notation:
 d[u] and f [u] always refer to first DFS.
 Extend notation for d and f to sets of vertices U  V:
 d(U) = minuU{d[u]} (earliest discovery time)
 f (U) = maxuU{ f [u]} (latest finishing time)
Dr. Hanif Durad 109

110. 110
SCCs and DFS finishing times
Proof:
 Case 1: d(C) < d(C)
» Let x be the first vertex discovered in
C.
» At time d[x], all vertices in C and C
are white. Thus, there exist paths of
white vertices from x to all vertices in
C and C.
» By the white-path theorem, all
vertices in C and C are descendants
of x in depth-first tree.
» By the parenthesis theorem, f [x] = f
(C) > f(C).
Lemma 22.14
Let C and C be distinct SCC’s in G = (V, E). Suppose there is an
edge (u, v)  E such that u  C and v C. Then f (C) > f (C).
C C
u v
x

111. 111
SCCs and DFS finishing times
Proof:
 Case 2: d(C) > d(C)
» Let y be the first vertex discovered in C.
» At time d[y], all vertices in C are white
and there is a white path from y to each
vertex in C  all vertices in C become
descendants of y. Again, f [y] = f (C).
» At time d[y], all vertices in C are also
white.
» By earlier lemma, since there is an edge
(u, v), we cannot have a path from C to
C.
» So no vertex in C is reachable from y.
» Therefore, at time f [y], all vertices in C
are still white.
» Therefore, for all w  C, f [w] > f [y],
which implies that f (C) > f (C).
Lemma 22.14
Let C and C be distinct SCC’s in G = (V, E). Suppose there is an
edge (u, v)  E such that u  C and v C. Then f (C) > f (C).
C C
u v
yx

112. 112
SCCs and DFS finishing times
Dr. Hanif Durad
Proof:
 (u, v)  ET  (v, u)  E.
 Since SCC’s of G and GT are the same, f(C) > f (C),
by Lemma 22.14.
Corollary 22.15
Let C and C be distinct SCC’s in G = (V, E). Suppose there is an edge
(u, v)  ET, where u  C and v  C. Then f(C) < f(C).

113. Correctness of SCC (1/3)
 When we do the second DFS, on GT, start with
SCC C such that f(C) is maximum.
 The second DFS starts from some x  C, and it visits
all vertices in C.
 Corollary 22.15 says that since f(C) > f (C) for all C
 C, there are no edges from C to C in GT.
 Therefore, DFS will visit only vertices in C.
 Which means that the depth-first tree rooted at x
contains exactly the vertices of C.
Dr. Hanif Durad 113

114. Correctness of SCC (2/3)
 The next root chosen in the second DFS is in
SCC C such that f (C) is maximum over all
SCC’s other than C.
 DFS visits all vertices in C, but the only edges out of
C go to C, which we’ve already visited.
 Therefore, the only tree edges will be to vertices in C.
 We can continue the process.
Dr. Hanif Durad 114

115. Correctness of SCC (3/3)
 Each time we choose a root for the second DFS,
it can reach only
 vertices in its SCC—get tree edges to these,
 vertices in SCC’s already visited in second DFS—get
no tree edges to these.
Dr. Hanif Durad 115