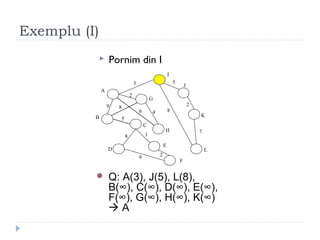
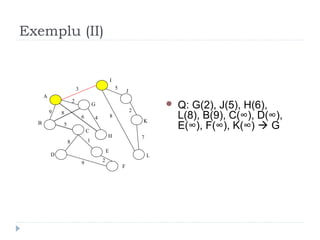
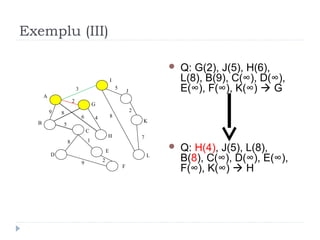
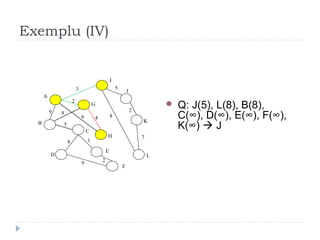
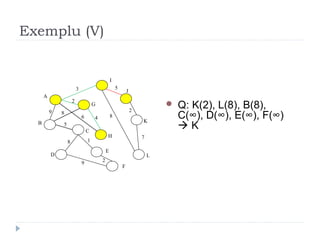
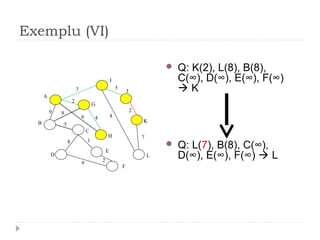
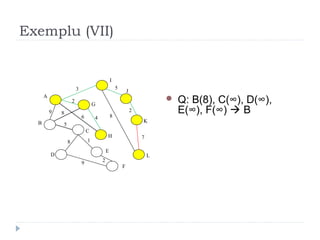
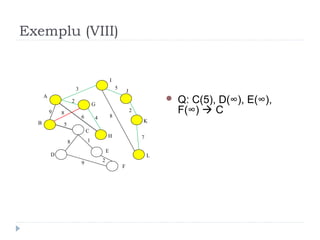
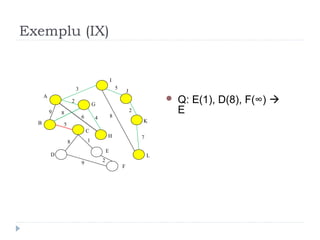
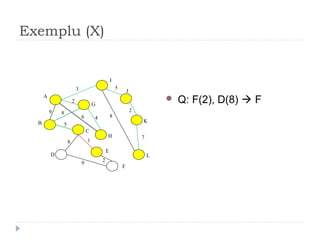
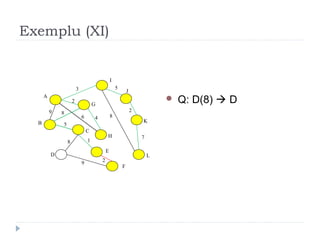
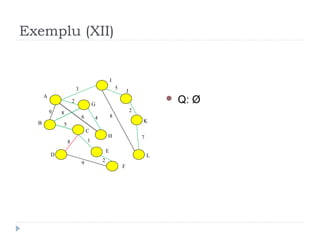
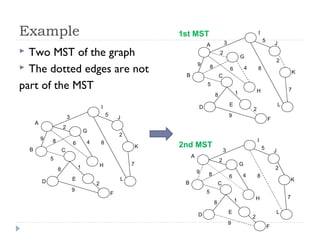
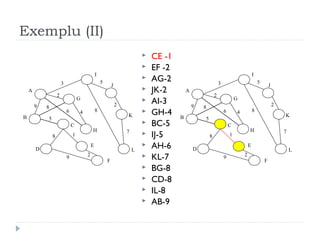
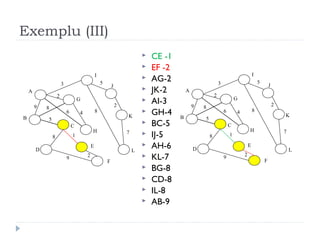
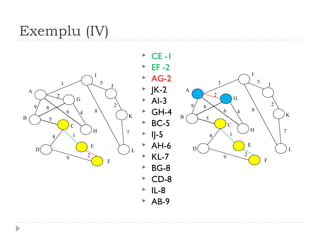
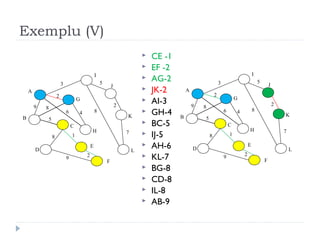
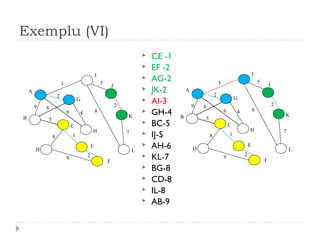
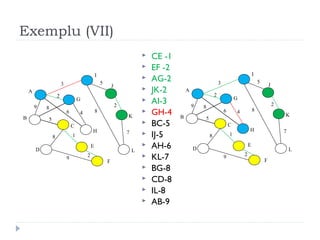
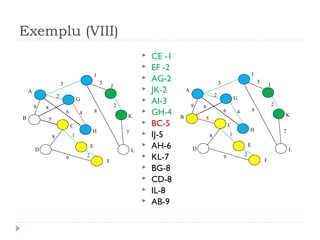
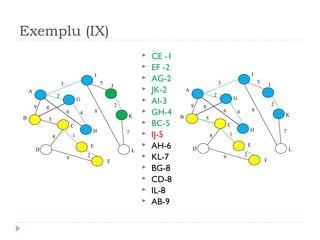
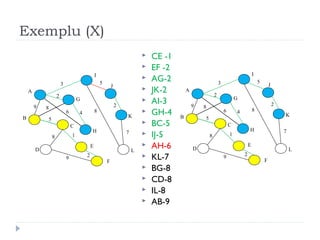
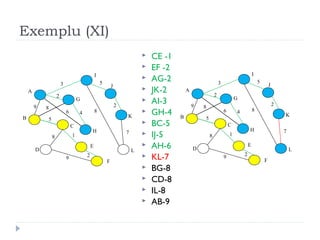
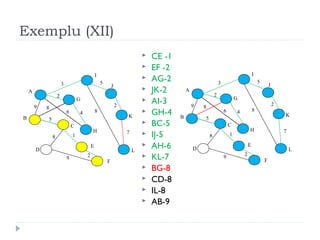
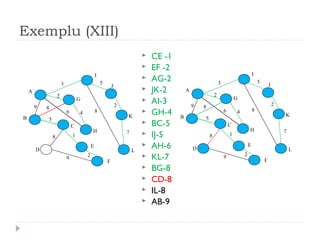
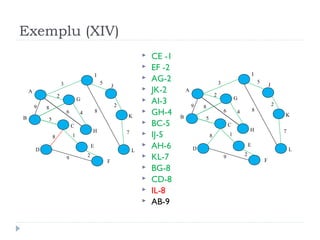
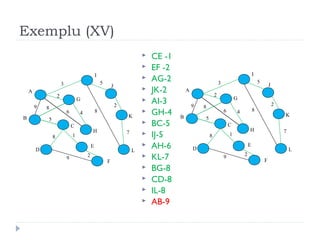
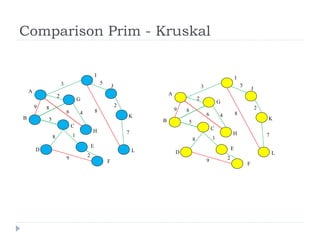
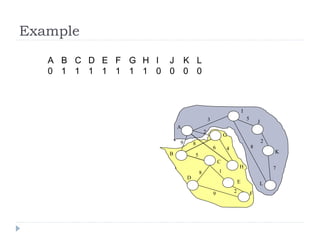
The document describes Kruskal's algorithm for finding the minimum spanning tree (MST) of a connected, undirected graph. Kruskal's algorithm works by sorting the edges by weight and then greedily adding edges to the MST one by one, skipping any edges that would create cycles. It uses the property that a minimum edge between disjoint components of the partial MST must be part of the overall MST. The runtime is O(ElogE) where E is the number of edges. An example run on a graph is shown step-by-step to demonstrate the algorithm.

1. Algorithm Design and
Complexity
Course 9

2. Overview






Minimum Spanning Trees
Generic Algorithm
Kruskal’s Algorithm
Disjoint Sets
Prim’s Algorithm
Fibonacci Heaps

3. Spanning Trees

G(V, E) undirected, connected and weighted graph

The weight (cost) function w: E → R
w(u, v) = the weight of the edge (u, v)


A spanning tree of G is a connected, undirected and
acyclic graph (a tree) that covers all the vertices of the
graph



T(V, E’), E’ ⊆ E
|E’| = |V| - 1
The weight of a spanning tree = the sum of the weights of
the edges that are part of the tree
 w(T) = Σ w(e), e ∈ E’

4. Minimum Spanning Trees

A minimum spanning tree (MST) is a spanning tree whose
total weight is minimized over all the possible spanning
trees that can be build for a given graph

Optimization problem





Does it have optimal substructure?
Are the sub-solutions optimal as well?
Maybe greedy or dynamic programming
A graph may have more than a single MST
We want to find only one of them

We can also find all of them, but is more difficult

5. Unique MST

If the weights of all the edges in the graph are distinct =>
unique MST

If there are two edges with the same weight => probably
there are more MSTs

A graph that has the same weight for all the edges => all
the spanning trees have the same cost

6. Example
1st MST
Two MST of the graph
 The dotted edges are not
part of the MST
I

5
3
A
2
9
8
G
A
2
9
8
B
8
K
5
9
2
9
L
2
5
3
7
H
1
E
F
I
2nd MST
A
8
L
2
9
J
C
D
E
2
4
6
7
H
1
D
G
K
5
I
5
8
C
8
3
2
4
6
B
J
8
G
2
4
6
B
J
8
K
C
5
F
D
E
9
7
H
1
8
L
2
F

7. MST – Applications

Computer networks
Road infrastructure
Other networks

Clustering in an Euclidian space

Approximation algorithms for NP-complete problems



E.g. for TSP

8. MST – Examples

Image source: http://hansolav.net/sql/prim_graph.png

9. MST – Solution

In order to find out the minimum spanning tree T(V, E’), we
need to find out the set of edges E’

Build an algorithm that builds a set of edges A
Initially, A is empty
At each step, we add an edge such that the following loop
invariant is respected:






A is a subset of a MST
Therefore, we add only edges that maintain the invariant.
These are called safe edges
If A is a subset of a MST, an edge (u,v)∈E is safe for A if and
only if A U {(u, v)} is also a subset of a MST for G
Optimal sub-structure!

10. MST – Generic Algorithm




Follows directly from the presented solution
The loop invariant is respected
However, it does not provide a way to select the safe
edges => the algorithm is not fully specified
Need to extend it in order to determine how to find the
safe edges
GENERIC-MST(G, w)
A=∅
WHILE (|A| < |V| – 1)
find an edge (u, v) that is safe for A
A = A U {(u, v)}
RETURN A

11. Finding Safe Edges

If A = ∅


If A != ∅




The edge with the lowest cost in G is safe for A = ∅
Let S ⊂ V the set of vertices covered by the edges in A
V S is not empty
The edge (c, f), c∈S, f∈V S, that has the minimum cost from
all the edges that have one endpoint in S and the other one in
V S
But these are greedy choices!

12. Definitions

A cut (S, V S) of a graph is a partition of vertices into two
disjoint sets






S
VS
An edge (u, v)∈E crosses the cut (S, V S) if it has one
endpoint in S and the other one in V S
A cut respects a set of edges A⊆E if no edge in A crosses the
cut
A light edge for a cut is one of the edges that crosses the cut
and has the minimum weight out of all the edges that cross
the cut
A cut has >= 1 light edges! They are not unique!

13. Theorem – Finding Safe Edges
A is a subset of a MST for G
 (S, V S) is a cut that respects A
 (u, v) is a light edge for the cut (S, V S)
Then
 (u, v) is a safe edge for A

Proof: Assume that we have
another MST T that does not
contain (u,v), but contains (x,y)
that crosses the cut. We can
build T’ = T {(x,y)} U {(u,v)}
which should also be a MST

14. Generic MST Revisited


Initially, A = ∅
Therefore, the partial MST contains all the vertices in G, but
no edges


=> We have a forest of |V| components, one vertex per component
At each step, we choose a safe edge that connects any two
components

Light edge for the cut that has one component in S and the other in
VS

The two connected components are merged into a larger
single connected component

Each component in the partial MST is a tree

In the end, we shall have a single component => the MST

15. Property

Let C = (Vc, Ec) a connected component in the partial
MST corresponding to the forest GA=(V, A)

(u, v) is a light edge connecting C with some other
component in GA


If (u, v) is a light edge for the cut (Vc, V Vc)
Then (u, v) is safe for A

Starting point for Kruskal’s algorithm

16. Kruskal’s Algorithm




Starts from the Generic MST algorithm
Sorts the edges of the graph according to their weight
Initially, A = ∅ and each vertex is in its own connected
component
Repeatedly merge two components into one by choosing the
light edge between them


This edge should also be a light edge for the cut between one of the
components and the rest of the graph
This is true if we consider the edges according to their
increasing weight

If the endpoints are in different components, then this is a safe edge!
Merge the two components

17. Kruskal – Pseudocode
KRUSKAL(G, w)
A=∅
FOREACH (v∈V)
MAKE-SET(v)
sort E by increasing order of their weights
FOREACH ((u, v)∈E taken from the sorted list)
IF (FIND-SET(u) != FIND-SET(v))
A = A U {(u, v)}
UNION(u, v)
RETURN A



// can also check if |A|<|V|-1
Complexity: Θ(m * logm + m * FIND-SET + n * UNION)
In the worst case, we consider all the edges in the graph, for
each of them we call FIND-SET twice!
UNION is always called O(n) times

18. Kruskal – Example


Example from “Proiectarea Algoritmilor 2010” course
Thanks to Costin Chiru 


I
5
3
A
2
9
B
8

G
6
4
C
K
H
1
9
2


7

E
D

2
8
5
8

J
L
F






CE -1
EF -2
AG-2
JK-2
AI-3
GH-4
BC-5
IJ-5
AH-6
KL-7
BG-8
CD-8
IL-8
AB-9

19. Exemplu (II)


I
5
3
A
2
9
B
8

J

G
6
2
8
4
K
5
H
1
7
E
D
9


C
8


L
2
F






CE -1
EF -2
AG-2
JK-2
AI-3
GH-4
BC-5
IJ-5
AH-6
KL-7
BG-8
CD-8
IL-8
AB-9
I
5
3
A
2
9
B
8
J
G
6
2
8
4
K
5
C
H
1
8
7
E
D
9
L
2
F

20. Exemplu (III)


I
5
3
A
2
9
B
8

J

G
6
2
8
4
K
5
H
1
7
E
D
9


C
8


L
2
F






CE -1
EF -2
AG-2
JK-2
AI-3
GH-4
BC-5
IJ-5
AH-6
KL-7
BG-8
CD-8
IL-8
AB-9
I
5
3
A
2
9
B
8
J
G
6
2
8
4
K
5
C
H
1
8
7
E
D
9
L
2
F

21. Exemplu (IV)


I
5
3
A
2
9
B
8

J

G
6
2
8
4
K
5
H
1
7
E
D
9


C
8


L
2
F






CE -1
EF -2
AG-2
JK-2
AI-3
GH-4
BC-5
IJ-5
AH-6
KL-7
BG-8
CD-8
IL-8
AB-9
I
5
3
A
2
9
B
8
J
G
6
2
8
4
K
5
C
H
1
8
7
E
D
9
L
2
F

22. Exemplu (V)


I
5
3
A
2
9
B
8

J

G
6
2
8
4
K
5
H
1
7
E
D
9


C
8


L
2
F






CE -1
EF -2
AG-2
JK-2
AI-3
GH-4
BC-5
IJ-5
AH-6
KL-7
BG-8
CD-8
IL-8
AB-9
I
5
3
A
2
9
B
8
J
G
6
2
8
4
K
5
C
H
1
8
7
E
D
9
L
2
F

23. Exemplu (VI)


I
5
3
A
2
9
B
8

J

G
6
2
8
4
K
5
H
1
7
E
D
9


C
8


L
2
F






CE -1
EF -2
AG-2
JK-2
AI-3
GH-4
BC-5
IJ-5
AH-6
KL-7
BG-8
CD-8
IL-8
AB-9
I
5
3
A
2
9
B
8
J
G
6
2
8
4
K
5
C
H
1
8
7
E
D
9
L
2
F

24. Exemplu (VII)


I
5
3
A
2
9
B
8

J

G
6
2
8
4
K
5
H
1
7
E
D
9


C
8


L
2
F






CE -1
EF -2
AG-2
JK-2
AI-3
GH-4
BC-5
IJ-5
AH-6
KL-7
BG-8
CD-8
IL-8
AB-9
I
5
3
A
2
9
B
8
J
G
6
2
8
4
K
5
C
H
1
8
7
E
D
9
L
2
F

25. Exemplu (VIII)


I
5
3
A
2
9
B
8

J

G
6
2
8
4
K
5
H
1
7
E
D
9


C
8


L
2
F






CE -1
EF -2
AG-2
JK-2
AI-3
GH-4
BC-5
IJ-5
AH-6
KL-7
BG-8
CD-8
IL-8
AB-9
I
5
3
A
2
9
B
8
J
G
6
2
8
4
K
5
C
H
1
8
7
E
D
9
L
2
F

26. Exemplu (IX)


I
5
3
A
2
9
B
8

J

G
6
2
8
4
K
5
H
1
7
E
D
9


C
8


L
2
F






CE -1
EF -2
AG-2
JK-2
AI-3
GH-4
BC-5
IJ-5
AH-6
KL-7
BG-8
CD-8
IL-8
AB-9
I
5
3
A
2
9
B
8
J
G
6
2
8
4
K
5
C
H
1
8
7
E
D
9
L
2
F

27. Exemplu (X)


I
5
3
A
2
9
B
8

J

G
6
2
8
4
K
5
H
1
7
E
D
9


C
8


L
2
F






CE -1
EF -2
AG-2
JK-2
AI-3
GH-4
BC-5
IJ-5
AH-6
KL-7
BG-8
CD-8
IL-8
AB-9
I
5
3
A
2
9
B
8
J
G
6
2
8
4
K
5
C
H
1
8
7
E
D
9
L
2
F

28. Exemplu (XI)


I
5
3
A
2
9
B
8

J

G
6
2
8
4
K
5
H
1
7
E
D
9


C
8


L
2
F






CE -1
EF -2
AG-2
JK-2
AI-3
GH-4
BC-5
IJ-5
AH-6
KL-7
BG-8
CD-8
IL-8
AB-9
I
5
3
A
2
9
B
8
J
G
6
2
8
4
K
5
C
H
1
8
7
E
D
9
L
2
F

29. Exemplu (XII)


I
5
3
A
2
9
B
8

J

G
6
2
8
4
K
5
H
1
7
E
D
9


C
8


L
2
F






CE -1
EF -2
AG-2
JK-2
AI-3
GH-4
BC-5
IJ-5
AH-6
KL-7
BG-8
CD-8
IL-8
AB-9
I
5
3
A
2
9
B
8
J
G
6
2
8
4
K
5
C
H
1
8
7
E
D
9
L
2
F

30. Exemplu (XIII)


I
5
3
A
2
9
B
8

J

G
6
2
8
4
K
5
H
1
7
E
D
9


C
8


L
2
F






CE -1
EF -2
AG-2
JK-2
AI-3
GH-4
BC-5
IJ-5
AH-6
KL-7
BG-8
CD-8
IL-8
AB-9
I
5
3
A
2
9
B
8
J
G
6
2
8
4
K
5
C
H
1
8
7
E
D
9
L
2
F

31. Exemplu (XIV)


I
5
3
A
2
9
B
8

J

G
6
2
8
4
K
5
H
1
7
E
D
9


C
8


L
2
F






CE -1
EF -2
AG-2
JK-2
AI-3
GH-4
BC-5
IJ-5
AH-6
KL-7
BG-8
CD-8
IL-8
AB-9
I
5
3
A
2
9
B
8
J
G
6
2
8
4
K
5
C
H
1
8
7
E
D
9
L
2
F

32. Exemplu (XV)


I
5
3
A
2
9
B
8

J

G
6
2
8
4
K
5
H
1
7
E
D
9


C
8


L
2
F






CE -1
EF -2
AG-2
JK-2
AI-3
GH-4
BC-5
IJ-5
AH-6
KL-7
BG-8
CD-8
IL-8
AB-9
I
5
3
A
2
9
B
8
J
G
6
2
8
4
K
5
C
H
1
8
7
E
D
9
L
2
F

33. Comparison Prim - Kruskal
I
3
A
2
9
B
8
I
5
J
A
G
6
2
8
4
C
H
1
8
9
B
8
6
F
4
K
5
H
1
8
2
2
8
C
L
J
G
7
E
D
2
9
K
5
5
3
7
E
D
9
L
2
F

34. Disjoint Sets


http://en.wikipedia.org/wiki/Disjoint-set_data_structure
We want to partition the vertices of the graph into a number
of separate and non-overlapping sets


To remember the connected components in the partial MST tree
Operations:



MAKE-SET(u): creates a set with a single element u
FIND-SET(u): finds the set that u is part of (usually returns the
representative element of that set, e.g. an ID of each set)
UNION(u, v): merges two distinct sets into a single one (need to
move all the elements of a set into the other one, in the end all the
elements in the new set must have the same representative)

35. Alternatives for Disjoint Sets

Can be implemented using lists, arrays, forest of trees
and forest of trees + heuristics

Simplest solutions: use arrays

set[1..n] = array with the representative of each element
in all the disjoint sets

36. Example
A B C D E F G H I J K L
0 1 1 1 1 1 1 1 0 0 0 0
I
5
3
A
2
9
8
B
J
G
6
8
4
2
K
5
C
D
H
1
8
7
E
9
2
L
F

37. Arrays as Disjoint Sets

Complexity?


MAKE-SET(u): Θ(1)
FIND-SET(u): Θ(1)


UNION(u, v): Θ(n)


Have to walk through all the elements of the smallest disjoint set and
change their representative to the one of the highest disjoint set!
Kruskal complexity?


Just return set[u]
Θ(m*logm + m + n2) = Θ(m*logm + n2)
Want better!

38. Forest of Trees as Disjoint Sets




Use a forest of trees
One tree for each disjoint set
The representative of the disjoint set is the root element of
each tree
Complexity?


MAKE-SET(u): Θ(1)
FIND-SET(u): Θ(max_height)



Need to return the root element
Start from u and walk up to the root
UNION(u, v): Θ(max_height)



Need to append all the elements in one tree to the other tree
Just make the root of the first tree point to an element in the second
tree (the root of the second tree or even to v)
But for this we need to find the root of the first tree

39. Forest of Trees as Disjoint Sets (2)

But, in the worst case

When unions are not made very wisely

max_height of a tree is O(n)
Therefore, the complexity of the two operations is O(n)

Need to improve it using heuristics:



Union by rank
Path compression

40. Heuristic 1: Union by Rank


Union wisely 
Always add the smallest tree to the root of the highest
one

This way, we keep the trees somewhat balanced and the
height does not increase a lot after multiple union
operations

It can be shown that max_height will be O(log n) in this
case

41. Heuristic 2: Path Compression

Flatten the tree whenever FIND-SET(u) is called

How?
Make all the elements on the path from u up to the root
of the tree point directly to the root
Thus, when we call FIND-SET for these elements, we can
return the root in Θ(1)


I
A
I
J
A
K
J
K
L
L

42. Forests with Both Heuristics


When using forests with union-by-rank and path-compression,
the average time of any operation on the disjoint set structure
(FIND-SET, UNION) is:
Θ(α(n)) = Θ(1) even for n – very large
α(n) = Ack-1(n, n)

Ack(m,n) = 2 ↑m-2 (n+3) – 3
A function that increases very, very quickly
Therefore α(n) increases very, very slowly

Kruskal complexity?



Θ(m*logm + m + n) = Θ(m*logm + n) = Θ(m*logn) WHY?

43. Prim’s Algorithm

Instead of building the partial MST in different connected
components
Build the partial MST in a single connected component S
Always consider the cut (S, V S) and choose the light
edge for this cut
Easier to implement?
Easier to understand?

Need a start vertex – it may be any vertex in G





44. Prim - Pseudocode
Prim(G, w, s)
FOREACH (v∈V)
p[v] = NULL; d[v] = INF;
d[s] = 0
A=∅
S=∅
Q = PRIORITY-QUEUE(V, d)
// used only to denote the cut
// build a priority queue indexed by the vertices V
// with priorities in d[u] for each vertex
WHILE (!Q.EMPTY())
u = Q.EXTRACT-MIN()
// pick the light edge = safe edge
S = S U {u}
// add the current vertex to the other side of the cut
A = A U {(u, p[u])}
// add the current edge to the partial MST
FOREACH (v∈Adj[u])
IF (d[v] > w(u,v))
// found a better edge from S to v
d[v] = w(u,v)
// need to heapify-up the element!
// Q.DECREASE-KEY(v, w(u,v))
p[v] = u
RETURN A {(s, p(s))}

45. Prim – Remarks




Uses a priority queue in order to allow finding the light
edge for the cut (S, V S) as efficiently as possible
The vertices that are in the priority queue are the ones
in V S
d[v] contains the minimum weight of an edge that
connects v with any vertex from S (true for each vertex
that is still in the priority queue)
(p[u], u) is exactly this minimum weight edge!

46. Prim – Complexity

Depends how we implement the priority queue:
Θ(n * EXTRACT-MIN + m * DECREASE-KEY)

If the priority queue is a simple array:





EXTRACT-MIN: O(n)
DECREASE-KEY: O(1)
Prim: Θ(n2 +m)  good for dense graphs
If the priority queue is a binary heap:



EXTRACT-MIN: O(logn)
DECREASE-KEY: O(logn)
Prim: Θ(nlogn +mlogn) = Θ(mlogn)  good for sparse graphs

47. Prim & Fibonacci Heaps


Best solution: use Fibonacci heaps
http://en.wikipedia.org/wiki/Fibonacci_heap



EXTRACT-MIN: O(logn)
DECREASE-KEY: O(1)
Prim: Θ(nlogn + m) = Θ(nlogn+m)  good for sparse and
dense graphs

48. Exemplu (I)

Pornim din I
I
5
3
A
2
9
B
8
G
6
2
8
4
K
5
C
H
1
8
7
E
D
9

J
L
2
F
Q: A(3), J(5), L(8),
B(∞), C(∞), D(∞), E(∞),
F(∞), G(∞), H(∞), K(∞)
A

49. Exemplu (II)
I
5
3
A
2
9
B
8
J

G
6
2
8
4
K
5
C
H
1
8
7
E
D
9
L
2
F
Q: G(2), J(5), H(6),
L(8), B(9), C(∞), D(∞),
E(∞), F(∞), K(∞)  G

50. Exemplu (III)

Q: G(2), J(5), H(6),
L(8), B(9), C(∞), D(∞),
E(∞), F(∞), K(∞)  G

Q: H(4), J(5), L(8),
B(8), C(∞), D(∞), E(∞),
F(∞), K(∞)  H
I
5
3
A
2
9
B
8
J
G
6
2
8
4
K
5
C
H
1
8
7
E
D
9
L
2
F

51. Exemplu (IV)
I
5
3
A
2
9
B
8
J

G
6
2
8
4
K
5
C
H
1
8
7
E
D
9
L
2
F
Q: J(5), L(8), B(8),
C(∞), D(∞), E(∞), F(∞),
K(∞)  J

52. Exemplu (V)
I
5
3
A
2
9
B
8
J

G
6
2
8
4
K
5
C
H
1
8
7
E
D
9
L
2
F
Q: K(2), L(8), B(8),
C(∞), D(∞), E(∞), F(∞)
K

53. Exemplu (VI)

Q: K(2), L(8), B(8),
C(∞), D(∞), E(∞), F(∞)
K

Q: L(7), B(8), C(∞),
D(∞), E(∞), F(∞)  L
I
5
3
A
2
9
B
8
J
G
6
2
8
4
K
5
C
H
1
8
7
E
D
9
L
2
F

54. Exemplu (VII)
I
5
3
A
2
9
B
8
J

G
6
2
8
4
K
5
C
H
1
8
7
E
D
9
L
2
F
Q: B(8), C(∞), D(∞),
E(∞), F(∞)  B

55. Exemplu (VIII)
I
5
3
A
2
9
B
8
J

G
6
2
8
4
K
5
C
H
1
8
7
E
D
9
L
2
F
Q: C(5), D(∞), E(∞),
F(∞)  C

56. Exemplu (IX)
I
5
3
A
2
9
B
8
J

G
6
2
8
4
K
5
C
H
1
8
7
E
D
9
L
2
F
Q: E(1), D(8), F(∞) 
E

57. Exemplu (X)
I
5
3
A
2
9
B
8
J

G
6
2
8
4
K
5
C
H
1
8
7
E
D
9
L
2
F
Q: F(2), D(8)  F

58. Exemplu (XI)
I
5
3
A
2
9
B
8
J

G
6
2
8
4
K
5
C
H
1
8
7
E
D
9
L
2
F
Q: D(8)  D

59. Exemplu (XII)
I
5
3
A
2
9
B
8
J

G
6
2
8
4
K
5
C
H
1
8
7
E
D
9
L
2
F
Q: Ø

60. References

CLRS – Chapter 24

R. Sedgewick, K Wayne – Algorithms and Data Structures –
Princeton 2007 www.cs.princeton.edu/~rs/AlgsDS07/
01UnionFind si 14MST

MIT OCW – Introduction to Algorithms – video lecture 16