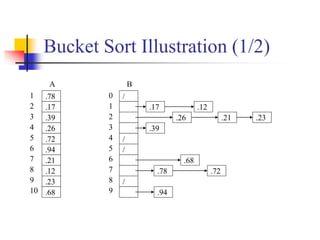
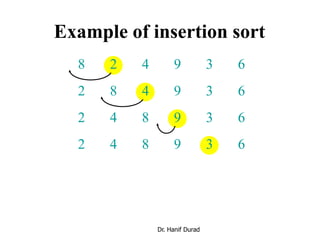
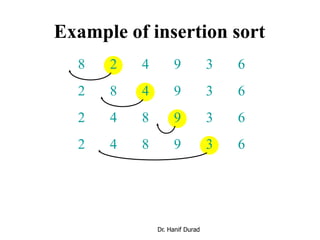
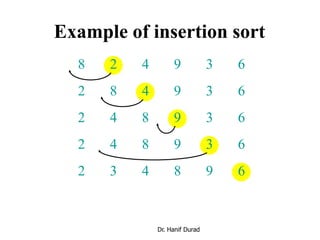
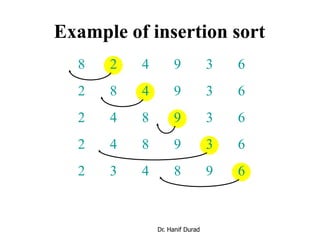
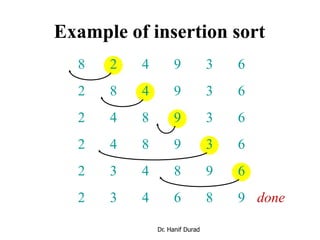
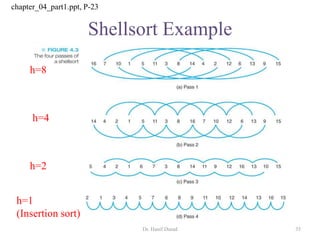
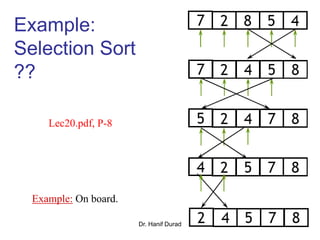
This document provides an overview of sorting algorithms including bubble sort, insertion sort, shellsort, and others. It discusses why sorting is important, provides pseudocode for common sorting algorithms, and gives examples of how each algorithm works on sample data. The runtime of sorting algorithms like insertion sort and shellsort are analyzed, with insertion sort having quadratic runtime in the worst case and shellsort having unknown but likely better than quadratic runtime.

1. Chapter 4
Sorting
Dr. Muhammad Hanif Durad
Department of Computer and Information Sciences
Pakistan Institute Engineering and Applied Sciences
hanif@pieas.edu.pk
Some slides have bee adapted with thanks from some other lectures
available on Internet. It made my life easier, as life is always
miserable at PIEAS (Sir Muhammad Yusaf Kakakhil )

2. Dr. Hanif Durad 2
Lecture Outline
 Why we do sorting?
1. Bubble Sort
2. Selection sort
3. Merge sort
4. Quick sort
5. Counting Sort
6. Radix Sort
7. Bucket Sort

3.  Commonly encountered programming task in
computing.
 Examples of sorting:
 List containing exam scores sorted from Lowest to Highest or
from Highest to Lowest
 List containing words that were misspelled and be listed in
alphabetical order.
 List of student records and sorted by student number or
alphabetically by first or last name.
Why we do sorting?
ISSort-AndyLe.ppt

4. Why we do sorting?
 Searching for an element in an array will be
more efficient. (example: looking up for
information like phone number).
 It’s always nice to see data in a sorted display.
(example: spreadsheet or database application).
 Computers sort things much faster.
ISSort-AndyLe.ppt

5. History of Sorting
 Sorting is one of the most important operations
performed by computers. In the days of magnetic tape
storage before modern databases, database updating was
done by sorting transactions and merging them with a
master file.
 It's still important for presentation of data extracted
from databases: most people prefer to get reports sorted
into some relevant order before flipping through pages
of data!
ISSort-AndyLe.ppt

6. Sorting – Definitions (1/3)
 Input: n records, R1 … Rn , from a file.
 Each record Ri has
 a key Ki
 possibly other (satellite) information
 The keys must have an ordering relation that satisfies
the following properties:
 Trichotomy: For any two keys a and b, exactly one of a b, a = b, or a b
is true.
 Transitivity: For any three keys a, b, and c, if a b and b c, then a c.
The relation = is a total ordering (linear ordering) on keys.
Dr. Hanif Durad 6

 
 

DSAL COMP 550-001, 04-sorting.ppt

7. Sorting – Definitions (2/3)
 Sorting: determine a permutation  = (p1, … , pn) of n
records that puts the keys in non-decreasing order Kp1
< … < Kpn.
 Permutation: a one-to-one function from
{1, …, n} onto itself. There are n! distinct
permutations of n items.
 Rank: Given a collection of n keys, the rank of a key is
the number of keys that precede it. That is, rank(Kj) =
|{Ki| Ki < Kj}|. If the keys are distinct, then the rank of
a key gives its position in the output file.
Dr. Hanif Durad 7

8. Sorting – Definitions (3/3)
 Internal (the file is stored in main memory and can be randomly
accessed) vs. External (the file is stored in secondary memory &
can be accessed sequentially only)
 Comparison-based sort: uses only the relation among keys, not
any special property of the representation of the keys themselves.
 Stable sort: records with equal keys retain their original relative
order; i.e., i < j & Kpi = Kpj  pi < pj
 Array-based (consecutive keys are stored in consecutive memory
locations) vs. List-based sort (may be stored in nonconsecutive
locations in a linked manner)
 In-place sort: needs only a constant amount of extra space in
addition to that needed to store keys.
Dr. Hanif Durad
8

9. The problem of sorting
Input: sequence a1, a2, …, an of numbers.
Example:
Input: 8 2 4 9 3 6
Output: 2 3 4 6 8 9
Output: permutation a'1, a'2, …, a'n such
that a'1  a'2 …  a'n .
l1.ppt
Dr. Hanif Durad

10. 1. Insertion sort
Dr. Hanif Durad 10

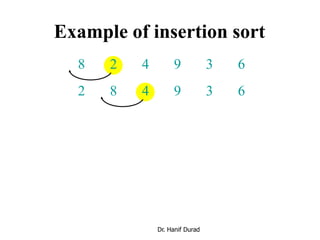
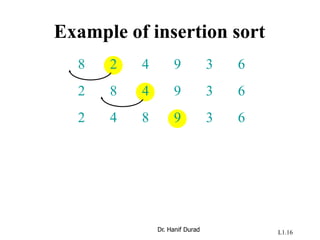
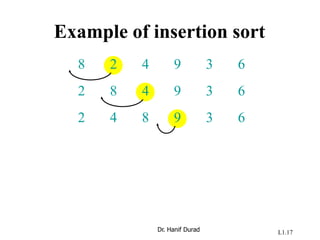
11. Insertion sort
INSERTION-SORT (A, n) ⊳ A[1 . . n]
for j ← 2 to n
do key ← A[ j]
i ← j – 1
while i > 0 and A[i] > key
do A[i+1] ← A[i]
i ← i – 1
A[i+1] = key
“pseudocode”
i j
key
sorted
A:
1 n
Dr. Hanif Durad

12. Example of insertion sort
8 2 4 9 3 6
Dr. Hanif Durad

13. Example of insertion sort
8 2 4 9 3 6
Dr. Hanif Durad

14. Example of insertion sort
8 2 4 9 3 6
2 8 4 9 3 6
Dr. Hanif Durad

15. Example of insertion sort
8 2 4 9 3 6
2 8 4 9 3 6
Dr. Hanif Durad

16. L1.16
Example of insertion sort
8 2 4 9 3 6
2 8 4 9 3 6
2 4 8 9 3 6
Dr. Hanif Durad

17. L1.17
Example of insertion sort
8 2 4 9 3 6
2 8 4 9 3 6
2 4 8 9 3 6
Dr. Hanif Durad

18. Example of insertion sort
8 2 4 9 3 6
2 8 4 9 3 6
2 4 8 9 3 6
2 4 8 9 3 6
Dr. Hanif Durad

19. Example of insertion sort
8 2 4 9 3 6
2 8 4 9 3 6
2 4 8 9 3 6
2 4 8 9 3 6
Dr. Hanif Durad

20. Example of insertion sort
8 2 4 9 3 6
2 8 4 9 3 6
2 4 8 9 3 6
2 4 8 9 3 6
2 3 4 8 9 6
Dr. Hanif Durad

21. Example of insertion sort
8 2 4 9 3 6
2 8 4 9 3 6
2 4 8 9 3 6
2 4 8 9 3 6
2 3 4 8 9 6
Dr. Hanif Durad

22. Example of insertion sort
8 2 4 9 3 6
2 8 4 9 3 6
2 4 8 9 3 6
2 4 8 9 3 6
2 3 4 8 9 6
2 3 4 6 8 9 done
Dr. Hanif Durad

23. Running time analysis
DesktopSortinginsertionsort(1).ppt
IA,P-25

24. Some explanation
 “times” column refers to how many times
each stmt is executed (max)
 n = length[A]
 tj = # times the while loop test in line 5 is
executed for that value of the index j

25. Best Case Analysis
T(n) = c1n + c2(n-1) + c4(n-1) + c5(n-1) +c8(n-1)
T(n) is a linear function of n
(array is already sorted)

26. Worst Case Analysis
So T(j) = j, for j = 2,3,…,n
Must compare each element A[j] w/ each element
in the entire sorted subarray A[1..j-1]
Thus, T(n) = c1n + c2(n-1) + c4(n-1) + c5(n(n+1)/2 – 1)
+ c6(n(n-1)/2) + c7(n(n-1)/2) + c8(n-1)
T(n) is a quadratic function of n
(array reverse-sorted)

27. O(N2) Runtime Example
Assume you are sorting 250,000,000 items
N = 250,000,000
N2 = 6.25 x 1016
If you can do one operation per
nanosecond (10-9 sec) which is fast!
It will take 6.25 x 107 seconds
So 6.25 x 107
60 x 60 x 24 x 365
= 1.98 years

28. 2. ShellSort
Dr. Hanif Durad 28

29. The idea of shellsort
 With insertion sort, each time we insert an element, other elements
get nudged one step closer to where they ought to be
 What if we could move elements a much longer distance each
time?
 We could move each element:
 A long distance
 A somewhat shorter distance
 A shorter distance still
 This approach is what makes shellsort so much faster than
insertion sort
17-shellsort.pptx

30. Sorting nonconsecutive subarrays
 Consider just the red locations
 Suppose we do an insertion sort on just these numbers, as
if they were the only ones in the array?
 Now consider just the yellow locations
 We do an insertion sort on just these numbers
 Now do the same for each additional group of numbers
• Here is an array to be sorted (numbers aren’t important)
• The resultant array is sorted within groups, but not overall

31. Doing the 1-sort
 In the previous slide, we compared numbers that were
spaced every 5 locations
 This is a 5-sort
 Ordinary insertion sort is just like this, only the numbers
are spaced 1 apart
 We can think of this as a 1-sort
 Suppose, after doing the 5-sort, we do a 1-sort?
 In general, we would expect that each insertion would involve
moving fewer numbers out of the way
 The array would end up completely sorted

32. Diminishing gaps
 For a large array, we don’t want to do a 5-sort; we want
to do an N-sort, where N depends on the size of the array
 N is called the gap size, or interval size
 We may want to do several stages, reducing the gap size
each time
 For example, on a 1000-element array, we may want
to do a 364-sort, then a 121-sort, then a 40-sort,
then a 13-sort, then a 4-sort, then a 1-sort
 Why these numbers?

33. The Knuth gap sequence
 No one knows the optimal sequence of diminishing gaps
 This sequence is attributed to Donald E. Knuth:
 Start with h = 1
 Repeatedly compute h = 3*h + 1
 1, 4, 13, 40, 121, 364, 1093
 Stop when h is larger than the size of the array and use as the first gap, the
previous number (364)
 To get successive gap sizes, apply the inverse formula:
h = (h – 1) / 3
 This sequence seems to work very well
 It turns out that just cutting the array size in half each time does
not work out as well

34. Shellsort
ShellSort(A, n)
1. h  1
2. while h  n {
3. h  3h + 1
4. }
5. repeat
6. h  h/3
7. for i = h to n do {
8. key  A[i]
9. j  i
10. while key < A[j - h] {
11. A[j]  A[j - h]
12. j  j - h
13. if j < h then break
14. }
15. A[j]  key
16. }
17. until h  1
Comp 122
When h=1, this is insertion sort.
Otherwise, performs insertion
sort on keys h locations apart.
h values are set in the outermost
repeat loop. Note that they are
decreasing and the final value is 1.
DSAL COMP 550-001, 04-sorting.ppt

35. Shellsort Example
Dr. Hanif Durad 35
chapter_04_part1.ppt, P-23
h=2
h=8
h=4
h=1
(Insertion sort)

36. Analysis (1/2)
 You cut the size of the array by some fixed amount, n, each time
 Consequently, you have about log n stages
 Each stage takes O(n) time
 Hence, the algorithm takes O(n log n) time
 Right?
 Wrong! This analysis assumes that each stage actually moves
elements closer to where they ought to be, by a fairly large amount
 What if all the red cells, for instance, contain the largest numbers in
the array?
 None of them get much closer to where they should be
 In fact, if we just cut the array size in half each time, sometimes we
get O(n2) behavior!

37. Analysis (2/2)
 So what is the real running time of shellsort?
 Nobody knows!
 Experiments suggest something like O(n3/2) or
O(n7/6)
 Analysis isn’t always easy!

38. 3. Bubble Sort
Dr. Hanif Durad 38

39. Bubble Sort
 If we compare pairs of adjacent elements and
none are out of order, the list is sorted
 If any are out of order, we must have to swap
them to get an ordered list
 Bubble sort will make passes though the list
swapping any adjacent elements that are out of
order
39
chapter_04_part1.ppt, P-12

40. Bubble Sort
 After the first pass, we know that the largest
element must be in the correct place
 After the second pass, we know that the second
largest element must be in the correct place
 Because of this, we can shorten each successive
pass of the comparison loop
40
chapter_04_part1.ppt, P-13

41. Bubble Sort Example
9, 6, 2, 12, 11, 9, 3, 7
6, 9, 2, 12, 11, 9, 3, 7
6, 2, 9, 12, 11, 9, 3, 7
6, 2, 9, 12, 11, 9, 3, 7
6, 2, 9, 11, 12, 9, 3, 7
6, 2, 9, 11, 9, 12, 3, 7
6, 2, 9, 11, 9, 3, 12, 7
6, 2, 9, 11, 9, 3, 7, 12The 12 is greater than the 7 so they are exchanged.
The 12 is greater than the 3 so they are exchanged.
The twelve is greater than the 9 so they are exchanged
The 12 is larger than the 11 so they are exchanged.
In the third comparison, the 9 is not larger than the 12 so no
exchange is made. We move on to compare the next pair without
any change to the list.
Now the next pair of numbers are compared. Again the 9 is the
larger and so this pair is also exchanged.
Bubblesort compares the numbers in pairs from left to right
exchanging when necessary. Here the first number is compared
to the second and as it is larger they are exchanged.
The end of the list has been reached so this is the end of the first pass. The
twelve at the end of the list must be largest number in the list and so is now in
the correct position. We now start a new pass from left to right.
bubblesortexample.ppt

42. Bubble Sort Example
6, 2, 9, 11, 9, 3, 7, 122, 6, 9, 11, 9, 3, 7, 122, 6, 9, 9, 11, 3, 7, 122, 6, 9, 9, 3, 11, 7, 122, 6, 9, 9, 3, 7, 11, 12
6, 2, 9, 11, 9, 3, 7, 12
Notice that this time we do not have to compare the last two
numbers as we know the 12 is in position. This pass therefore only
requires 6 comparisons.
First Pass
Second Pass

43. Bubble Sort Example
2, 6, 9, 9, 3, 7, 11, 122, 6, 9, 3, 9, 7, 11, 122, 6, 9, 3, 7, 9, 11, 12
6, 2, 9, 11, 9, 3, 7, 12
2, 6, 9, 9, 3, 7, 11, 12
Second Pass
First Pass
Third Pass
This time the 11 and 12 are in position. This pass therefore only
requires 5 comparisons.

44. Bubble Sort Example
2, 6, 9, 3, 7, 9, 11, 122, 6, 3, 9, 7, 9, 11, 122, 6, 3, 7, 9, 9, 11, 12
6, 2, 9, 11, 9, 3, 7, 12
2, 6, 9, 9, 3, 7, 11, 12
Second Pass
First Pass
Third Pass
Each pass requires fewer comparisons. This time only 4 are needed.
2, 6, 9, 3, 7, 9, 11, 12Fourth Pass

45. Bubble Sort Example
2, 6, 3, 7, 9, 9, 11, 122, 3, 6, 7, 9, 9, 11, 12
6, 2, 9, 11, 9, 3, 7, 12
2, 6, 9, 9, 3, 7, 11, 12
Second Pass
First Pass
Third Pass
The list is now sorted but the algorithm does not know this until it
completes a pass with no exchanges.
2, 6, 9, 3, 7, 9, 11, 12Fourth Pass
2, 6, 3, 7, 9, 9, 11, 12Fifth Pass

46. Bubble Sort Example
2, 3, 6, 7, 9, 9, 11, 12
6, 2, 9, 11, 9, 3, 7, 12
2, 6, 9, 9, 3, 7, 11, 12
Second Pass
First Pass
Third Pass
2, 6, 9, 3, 7, 9, 11, 12Fourth Pass
2, 6, 3, 7, 9, 9, 11, 12Fifth Pass
Sixth Pass
2, 3, 6, 7, 9, 9, 11, 12
This pass no exchanges are made so the algorithm knows the list is
sorted. It can therefore save time by not doing the final pass. With
other lists this check could save much more work.

47. Bubble Sort Algortithm
1. for i←1 to length[A]
2. for j←length[A] down to i+1
3. if (A[j] < A[j-1])
4. swap(A[j] ,A[j-1]);
Dr. Hanif Durad 47
DS-1, P-453

48. Best-Case Analysis
 If the elements start in sorted order, the for loop
will compare the adjacent pairs but not make
any changes
 There are N – 1 comparisons in the best case
48
chapter_04_part1.ppt, P-16 modified according to DS-1,P453

49. Worst-Case Analysis
 If in the best case the outer loop is done
once, in the worst case the outer loop
must be done as many times as possible
 Each pass of the for loop must make at least
one swap of the elements
 The number of comparisons will be:
49
 
1
2
1
( 1)*
T( ) O
2i N
n n
n i n
 

  
chapter_04_part1.ppt, P-17 modified according to DS-1,P453

50. Bubble Sort Quiz
1. Which number is definitely in its correct position at the end of the
first pass?
 Answer: The last number must be the largest.
2. How does the number of comparisons required change as the pass
number increases?
 Answer: Each pass requires one fewer comparison than the last.
3. How does the algorithm know when the list is sorted?
 Answer: When a pass with no exchanges occurs.
4. What is the maximum number of comparisons required for a list of
10 numbers?
 Answer: 9 comparisons, then 8, 7, 6, 5, 4, 3, 2, 1 so total 45
Dr. Hanif Durad 50
bubblesortexample.ppt

51. 4. Selection sort
Dr. Hanif Durad 51

52. Selection sort
 How does it work:
 first find the smallest in the array and exchange it with the
element in the first position, then find the second smallest
element and exchange it with the element in the second
position, and continue in this way until the entire array is
sorted.
 How does it sort the list in a non increasing order?
 Selection sort is:
 The simplest sorting techniques.
 a good algorithm to sort a small number of elements
 an incremental algorithm – induction method
C:Documents and SettingsAdministratorDesktopSortingCS251-lecture3-Sort.ppt

53. Selection sort
 Selection sort is Inefficient for large lists.
Incremental algorithms
process the input elements one-by-one and maintain
the solution for the elements processed so far.
CS251-lecture3-Sort.ppt

54. Selection Sort Algorithm
Input: An array A[1..n] of n elements.
Output: A[1..n] sorted in nondecreasing order.
1. for i  1 to n - 1
2. k  i
3. for j  i + 1 to n {Find the i th smallest element.}
4. if A[j] < A[k] then k  j
5. end for
6. if k  i then interchange A[i] and A[k]
7. end for

55. Analysis of Algorithms
 Algorithm analysis: quantify the performance of the algorithm,
i.e., the amount of time and space taken in terms of n.
 T(n) is the total number of accesses made from the beginning of
selection_sort until the end.
 selection_sort itself simply calls swap and find_min_index as i
goes from 1 to n-1




1
1
min)(
n
i
swapelementfindnT
= n-1 + n-2 + n-3 + … + 1 = n(n-1)/2
Or = ∑ (n - i) = n (n - 1) / 2 - O(n2)

56. Dr. Hanif Durad 56
Example:
Selection Sort
??
Lec20.pdf, P-8
Example: On board.

57. 5. Merge sort
(Divide and conquer)
Dr. Hanif Durad 57

58. Divide and Conquer
 Recursive in structure
 Divide the problem into sub-problems that are
similar to the original but smaller in size
 Conquer the sub-problems by solving them
recursively. If they are small enough, just solve
them in a straightforward manner.
 Combine the solutions to create a solution to the
original problem
Dr. Hanif Durad 58

59. An Example: Merge Sort
Sorting Problem: Sort a sequence of n elements into non-
decreasing order.
 Divide: Divide the n-element sequence to be sorted into
two subsequences of n/2 elements each
 Conquer: Sort the two subsequences recursively using
merge sort.
 Combine: Merge the two sorted subsequences to
produce the sorted answer.
Dr. Hanif Durad 59

60. Merge Sort – Example
1
8
2
6
3
2
6 4
3
1
5
9 1
1
8
2
6
3
2
6 4
3
1
5
9 1
1
8
2
6
3
2
6 4
3
1
5
9 1
2618 632 1543 19
26 32 6 43 15 9 1
18 26 32 6 4 15 9 1
18 26 326 15 43 1 9
6 18 26 32 1 9 15 43
1 6 9 15 18 26 32 43
26
18 26
1
8
2
6
32
32
6
6
3
2
6
1
8
2
6
3
2
6
43
43
15
15
4
3
1
5
9
9
1
1
9 1
4
3
1
5
9 1
1
8
2
6
3
2
6 4
3
1
5
9 1
18 26 632
626 3218
1543 19
1 915 43
16 9 1518 26 32 43
Original Sequence Sorted Sequence

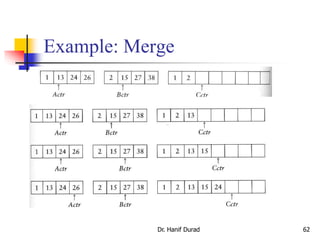
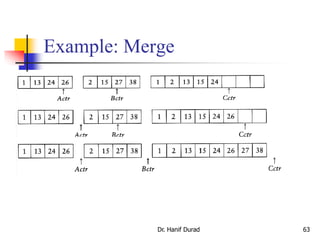
61. How to merge two Arrays?
Dr. Hanif Durad 61
 Input: two sorted array A and B
 Output: an output sorted array C
 Three counters: Actr, Bctr, and Cctr
 initially set to the beginning of their respective arrays
(1) The smaller of A[Actr] and B[Bctr] is copied to the next entry in C,
and the appropriate counters are advanced
(2) When either input list is exhausted, the remainder of the other list is
copied to C
D:DSALCOMP171 Data Structures and Algorithmmergesort.ppt

62. Example: Merge
Dr. Hanif Durad 62

63. Example: Merge
Dr. Hanif Durad 63

64. Running Time Analysis
 Clearly, merge takes O(m1 + m2) where m1 and
m2 are the sizes of the two sub lists.
 Space requirement:
 merging two sorted lists requires linear extra
memory
 additional work to copy to the temporary array and
back
Dr. Hanif Durad 64

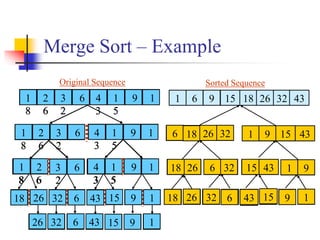
65. Merge Sort Algorithm
 The procedure MERGE-SORT(A, p, r) sorts the elements in the
sub-array A[ p…r].
 The divide step simply computes an index q that partitions A[ p…r]
into two sub-arrays: A[ p…q], containing n/2 elements, and A[ q +
1…r], containing n/2 elements.
 To sort the entire sequence A ={A[1], A[2], . . . ,
A[ n]}, we make the initial call MERGE-SORT( A, 1, length[ A]),
where length[ A] = n.
02_Getting Started_2.ppt

66. L1.66
66
// Copy A[p, q] to L
// Copy A[q+1, r] to R
// Compute # of elements in L
// Compute # of elements in R
// Put a sentinel card at the end of L
// Put a sentinel card at the end of R
// Put the smaller of
L[i] and R[j] to A[K
unit03.ppt

67. 67
Merge Sort
 The key operation of the merge sort algorithm is the
merging of two sorted sequences in the "combine" step. To
perform the merging, we use an auxiliary procedure
MERGE(A, p, q, r), where A is an array and p, q, and r
are indices numbering elements of the array such that p ≤ q
< r.
 The procedure assumes that the sub-arrays A[ p…q] and
A[ q + 1…r] are in sorted order. It merges them to form a
single sorted sub-array that replaces the current sub-array
A[ p…r].

68. 68
Merge Example (1/2)
 The operation of lines 10-17 in the call MERGE(A, 9, 12, 16).
Example: On board. DS-1,P-470

69. 69
Merge Example (2/2)
 The operation of lines 10-17 in the call MERGE(A, 9, 12, 16)

70. Analyzing Merge Sort
Statement Effort
Dr. Hanif Durad 70
So T(n) = (1) when n = 1, and
2T(n/2) + (n) when n > 1
MergeSort(A, left, right) { T(n)
if (left < right) { (1)
mid = floor((left + right) / 2); (1)
MergeSort(A, left, mid); T(n/2)
MergeSort(A, mid+1, right); T(n/2)
Merge(A, left, mid, right); (n)
}
}

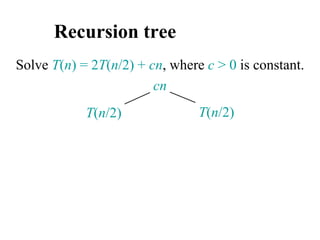
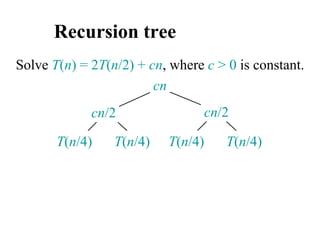
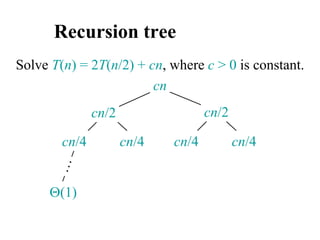
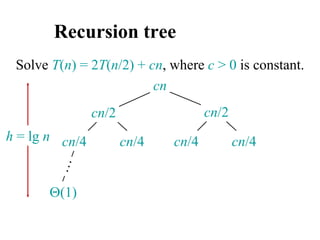
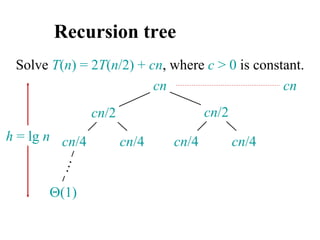
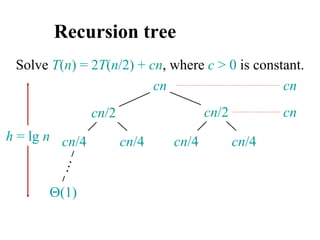
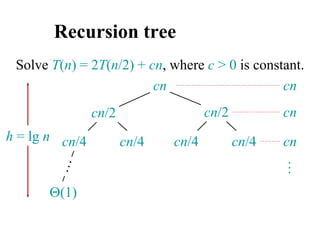
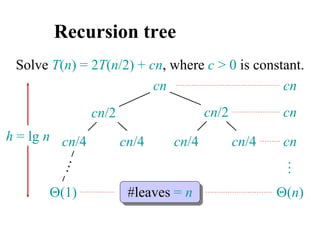
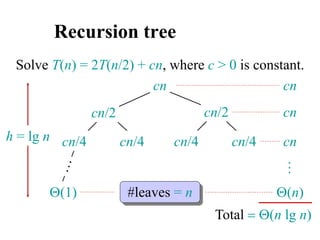
71. Analyzing merge sort
MERGE-SORT A[1 . . n]
1. If n = 1, done.
2. Recursively sort A[ 1 . . n/2 ]
and A[ n/2+1 . . n ] .
3. “Merge” the 2 sorted lists
T(n)
(1)
2T(n/2)
(n)
Sloppiness: Should be T( n/2 ) + T( n/2 ) ,
but it turns out not to matter asymptotically.

72. Recurrence for merge sort
T(n) =
(1) if n = 1;
2T(n/2) + (n) if n > 1.
• We shall usually omit stating the base
case when T(n) = (1) for sufficiently
small n, but only when it has no effect on
the asymptotic solution to the recurrence.

73. Recursion tree
Solve T(n) = 2T(n/2) + cn, where c > 0 is constant.

74. Recursion tree
Solve T(n) = 2T(n/2) + cn, where c > 0 is constant.
T(n)

75. Recursion tree
Solve T(n) = 2T(n/2) + cn, where c > 0 is constant.
T(n/2) T(n/2)
cn

76. Recursion tree
Solve T(n) = 2T(n/2) + cn, where c > 0 is constant.
cn
T(n/4) T(n/4) T(n/4) T(n/4)
cn/2 cn/2

77. Recursion tree
Solve T(n) = 2T(n/2) + cn, where c > 0 is constant.
cn
cn/4 cn/4 cn/4 cn/4
cn/2 cn/2
(1)

78. Recursion tree
Solve T(n) = 2T(n/2) + cn, where c > 0 is constant.
cn
cn/4 cn/4 cn/4 cn/4
cn/2 cn/2
(1)
h = lg n

79. Recursion tree
Solve T(n) = 2T(n/2) + cn, where c > 0 is constant.
cn
cn/4 cn/4 cn/4 cn/4
cn/2 cn/2
(1)
h = lg n
cn

80. Recursion tree
Solve T(n) = 2T(n/2) + cn, where c > 0 is constant.
cn
cn/4 cn/4 cn/4 cn/4
cn/2 cn/2
(1)
h = lg n
cn
cn

81. Recursion tree
Solve T(n) = 2T(n/2) + cn, where c > 0 is constant.
cn
cn/4 cn/4 cn/4 cn/4
cn/2 cn/2
(1)
h = lg n
cn
cn
cn
…

82. Recursion tree
Solve T(n) = 2T(n/2) + cn, where c > 0 is constant.
cn
cn/4 cn/4 cn/4 cn/4
cn/2 cn/2
(1)
h = lg n
cn
cn
cn
#leaves = n (n)
…

83. Recursion tree
Solve T(n) = 2T(n/2) + cn, where c > 0 is constant.
cn
cn/4 cn/4 cn/4 cn/4
cn/2 cn/2
(1)
h = lg n
cn
cn
cn
#leaves = n (n)
Total (n lg n)
…

84. Conclusions
• (n lg n) grows more slowly than (n2).
• Therefore, merge sort asymptotically
beats insertion sort in the worst case.
• In practice, merge sort beats insertion
sort for n > 30 or so.

85. O(NLogN) Runtime Example
Assume same 250,000,000 items
N*Log(N) = 250,000,000 x 8.3
= 2, 099, 485, 002
With the same processor as before
2 seconds
See back slide 27

86. 6. Quick sort
(Divide and Conquer)
Dr. Hanif Durad 86

87. Introduction
 Another divide-and-conquer recursive algorithm, like
mergesort
 Quicksort pros [advantage]:
 Sorts in place
 Sorts O(n lg n) in the average case
 Very efficient in practice , it’s quick
 Quicksort cons [disadvantage]:
 Sorts O(n2) in the worst case
 And the worst case doesn’t happen often … sorted
Dr. Hanif Durad 87
D:DSALCOMP171 Data Structures and Algorithmqsort.ppt
C:Documents and SettingsAdministratorDesktopSortingquicksortalgo_Lecture 6 quick_sor.ppt

88.  Divide step:
 Pick any element (pivot) v in S
 Partition S – {v} into two disjoint
groups
S1 = {x  S – {v} | x <= v}
S2 = {x  S – {v} | x  v}
 Conquer step: recursively sort S1 and
S2
 Combine step: the sorted S1 (by the
time returned from recursion), followed
by v, followed by the sorted S2 (i.e.,
nothing extra needs to be done)
v
v
S1 S2
S
QuickSort
D:DSALCOMP171 Data Structures and Algorithmqsort.ppt
Dr. Hanif Durad

89. Quicksort Example 1 (1/2)
Dr. Hanif Durad

90. Quicksort Example 1 (2/2)
Dr. Hanif Durad

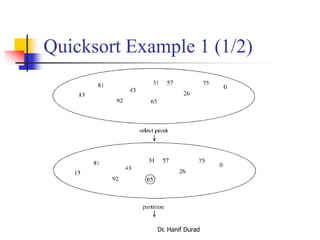
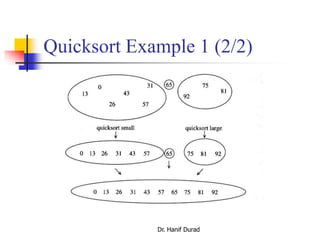
91. Quicksort Example 2 (1/7)
150 300 650 550 800 400 350 450
scanUp scanDown
v[0] v[9]v[8]v[7]v[6]v[5]v[4]v[3]v[2]v[1]
pivot
500 900
 The quicksort algorithm uses a series of recursive calls to partition a
list into smaller and smaller sublists about a value called the pivot.
 Example: Let v be a vector containing 10 integer values:
 v = {800, 150, 300, 650, 550, 500, 400, 350, 450,
900}
D:DSALCLRlect6
Dr. Hanif Durad

92. Quicksort Example 2 (3/7)
Before the exchange
After the exchange and updates to scanUp and scanDown
150 300 650 550 800 400 350 450
scanUp scanDown
v[0] v[9]v[8]v[7]v[6]v[5]v[4]v[3]v[2]v[1]
pivot
500 900
150 300 450 550 800 400 350 650
scanUp scanDown
v[0] v[9]v[8]v[7]v[6]v[5]v[4]v[3]v[2]v[1]
pivot
500 900
Dr. Hanif Durad

93. Quicksort Example 2 (3/7)
Before the exchange
After the exchange and updates to scanUp and scanDown
150 300 450 550 800 400 350 650
scanUp scanDown
v[0] v[9]v[8]v[7]v[6]v[5]v[4]v[3]v[2]v[1]
pivot
500 900
150 300 450 350 800 400 550 650
scanUp scanDown
v[0] v[9]v[8]v[7]v[6]v[5]v[4]v[3]v[2]v[1]
pivot
500 900
Dr. Hanif Durad

94. Quicksort Example 2 (4/7)
Before the exchange
After the exchange and updates to scanUp and scanDown
150 300 450 350 800 400 550 650
scanUp scanDown
v[0] v[9]v[8]v[7]v[6]v[5]v[4]v[3]v[2]v[1]
pivot
500 900
150 300 450 350 400 800 550 650
scanUpscanDown
v[0] v[9]v[8]v[7]v[6]v[5]v[4]v[3]v[2]v[1]
pivot
500 900
Dr. Hanif Durad

95. Quicksort Example 2 (4/7)
400 150 300 450 350 500 800 550 650
v[0] v[9]v[8]v[7]v[6]v[5]v[4]v[3]v[2]v[1]
900
Pivot in its final position
400 150 300 450 350 500 800 550 650
v[0] v[9]v[8]v[7]v[6]v[5]v[4]v[3]v[2]v[1]
v[0] - v[4] v[6] - v[9]
900
Dr. Hanif Durad

96. Quicksort Example 2 (5/7)
pivot
300 150 400 450 350
scanUp
v[0] v[4]v[3]v[2]v[1]
Initial Values
scanDown
pivot
300 150 400 450 350
v[0] v[4]v[3]v[2]v[1]
scanUp
After Scans Stop
scanDown
150 300 400 450 350
v[0] v[4]v[3]v[2]v[1]
Dr. Hanif Durad

97. pivot
650 550 800 900
scanUp
v[6] v[9]v[8]v[7]
Initial Values
scanDown
pivot
650 550 800 900
v[6] v[9]v[8]v[7]
scanUp
After Stops
scanDown
550 650 800 900
v[6] v[9]v[8]v[7]
Quicksort Example 2 (6/7)
Dr. Hanif Durad

98. Quicksort Example 2 (7/7)
v[0] v[4]v[3]v[2]v[1] v[6] v[9]v[8]v[7]v[5]
150 900800650550500350450400300
400 450 350
v[4]v[3]v[2]
Before Partitioning
350 400 450
v[4]v[3]v[2]
After Partitioning
150 300 350 400 450 500
v[0] v[4]v[3]v[2]v[1]
550 650 800 900
v[6] v[9]v[8]v[7]v[5]
Dr. Hanif Durad

99. QuickSort
Like in MERGESORT, we use Divide-and-Conquer:
1. Divide: partition A[p..r] into two subarrays A[p..q-1] and
A[q+1..r] such that each element of A[p..q-1] is ≤ A[q], and each
element of A[q+1..r] is ≥ A[q]. Compute q as part of this
partitioning.
2. Conquer: sort the subarrays A[p..q-1] and A[q+1..r] by recursive
calls to QUICKSORT.
3. Combine: the partitioning and recursive sorting leave us with a
sorted A[p..r] – no work needed here.
An obvious difference is that we do most of the work in the divide
stage, with no work at the combine one.
C:Documents and SettingsAdministratorDesktopSortingquicksortAlgorithms-Ch7.ppt

100. The Pseudo-Code
QuickSort
C:Documents and SettingsAdministratorDesktopSortingquicksortAlgorithms-Ch7.ppt

101. QuickSort
Example: IA,P-147 On board from Notes
Example: DS-1,P-478
Example: DS-2,P-478
C:Documents and SettingsAdministratorDesktopSortingquicksortAlgorithms-Ch7.ppt

102. Analysis of QuickSort (1/2)
 Levels in call tree (log n)
 Elements at each level (average case)
 Level 0 (1 vector of n elements)
 Level 1 (2 vectors of approx. n/2 elements)
 Level 2 (4 vectors of approx. n/4 elements)
 ….
 Level k (2k vectors of approx. n/2k elements)
 Each level has n elements & O(n) effort required to find all pivotIndexes
& partitions at each level
 There are approx. k = log n level
 QuickSort is O(n log n) in best and average cases

103. Analysis of QuickSort-Worst
Case (2/2)
 If pivot is largest or smallest value
 One sub-vector will be empty
 The other will contain n-1 values
 If this happens at every level of recursion
 The call tree has n-1 rather than log n levels
 The effort to find the pivot Index is then
 (n-1) + (n-2) + … + 2 + 1
 So quicksort is O(n2) in the worst case
 It is easy to see how this could happen if the first value is chosen as the
pivot and the array is already sorted.

104. 7. Counting Sort
Dr. Hanif Durad 106
D:DSAL5165 Advanced Algorithm and Programming Languageunit08.ppt

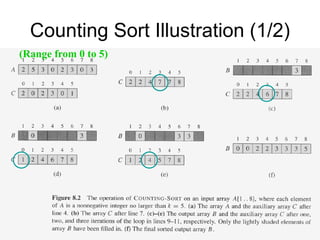
105. Counting Sort Overview
 Assumption: n input elements are integers in the range of 0
to k (integer).
 (n+k)  When k=O(n), counting sort: (n)
 Basic Idea
 For each input element x, determine the number of elements less
than or equal to x
 For each integer i (0  i  k), count how many elements whose
values are i
 Then we know how many elements are less than or equal to i
 Algorithm storage
 A[1..n]: input elements
 B[1..n]: sorted elements
 C[0..k]: hold the number of elements less than or equal to i

106. Counting Sort Illustration (1/2)
108
(Range from 0 to 5)

107. Counting Sort Illustration (2/2)
2 5 3 0 2 3 0 3A 0 3 3B
1 2 4 5 7 8C
0 2 3 3B
1 2 3 5 7 8C
0 0 2 3 3B
0 2 3 5 7 8C
0 0 2 3 3 3B
0 2 3 4 7 8C
0 0 2 3 3 3 8B
0 2 3 4 7 7C
0 0 2 2 3 3 3 8
0 2 3 4 7 7C
B
2
4
0
1
3
5
5
8
2
2

108. Counting Sort Algorithm
(k)
(n)
(k)
(n)
(n+k)

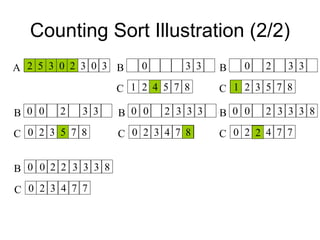
109. Counting Sort Is Stable
 A sorting algorithm is stable if
 Numbers with the same value appear in the output array
in the same order as they do in the input array
 Ties between two numbers are broken by the rule that
which ever number appears first in the input array
appears first in the output array
 Line 9 of counting sort: for jlength[A] down to 1
is essential for counting sort to be stable
 What if for j  1 to length[A]

110. 8. Radix Sort
Dr. Hanif Durad 112

111. Radix Sort Illustration
1. Sort on the least significant digit first
2. It is essential that the digit sorts in this algorithm be stable
(why?)

112. Radix Sort Algorithm
d digits in
total
Lemma 8.3 Given n d-digit numbers in which each digit can take on
up to k possible
values, RADIX-SORT correctly sorts these numbers in (d(n+k))
time
 Correctness: Exercise 8.3-3
 Use counting sort to sort each digit: (n+k)
 When d is constant and k=O(n)  (n)

113. 9. Bucket Sort
Dr. Hanif Durad 115

114. Bucket Sort Overview
 Bucket sort runs in linear time when the input is
drawn from a uniform distribution over the interval
[0, 1)
 Basic idea
 Divide [0,1) into n equal-sized subintervals (buckets)
 Distribute the n numbers into the buckets
 Sort the numbers in each bucket
 Go through the buckets in order, list the elements in
each

115. Bucket Sort Illustration (1/2)
.78
.17
.39
.26
.72
.94
.21
.12
.23
.68
/
/
/
/
A B
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
6
7
8
9
.17 .12
.26 .21 .23
.39
.78
.94
.68
.72

116. Bucket Sort Illustration (2/2)
118

117. 119
Bucket Sort Algorithm
As long as the input has the property that the sum of the squares
of the bucket size is linear in the total number of elements,
bucket sort will run in linear time