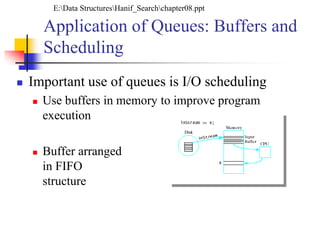
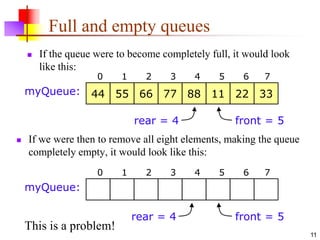
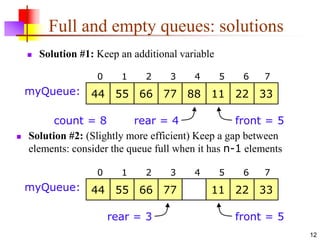
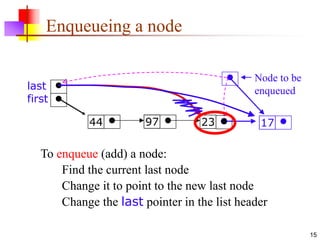
This document discusses queues and their applications. It begins by defining queues as first-in, first-out (FIFO) data structures and describes how they can be implemented using arrays or linked lists. Common applications of queues include I/O buffering, job scheduling, and round-robin threading. The document also covers double-ended queues (deques), priority queues, and their implementations and applications.

1. Chapter 7
QUEUES
Dr. Muhammad Hanif Durad
Department of Computer and Information Sciences
Pakistan Institute Engineering and Applied Sciences
hanif@pieas.edu.pk
Some slides have bee adapted with thanks from some other lectures
available on Internet. It made my life easier, as life is always
miserable at PIEAS (Sir Muhammad Yusaf Kakakhil )

2. Dr. Hanif Durad 2
Lecture Outline
 Queues
 Deques
 Priority Queue

3. Visualization of a Queue
Dr. Hanif Durad 3
D:Data StructuresPRG DS CS11001L9-3.pdf

4. 4
Queues, and Deques
 A queue is a first in, first out (FIFO) data structure
 Items are removed from a queue in the same order as they
were inserted
 A deque is a double-ended queue—items can be
inserted and removed at either end
D:Data StructuresHanif_SearchQueues23-stacks-queues-deques.ppt

5. Queue Applications
 Real life examples
 Waiting in line
 Waiting on hold for tech support
 Applications related to Computer Science
 Threads
 Job scheduling (e.g. Round-Robin algorithm for
CPU allocation)
Dr. Hanif Durad 5
D:Data StructuresCSCE3110Queues.ppt

6. 6
Queues (1/2)
 A queue differs from a stack in that its insertion and removal
routines follows the first-in-first-out (FIFO) principle.
 Elements may be inserted at any time, but only the element which
has been in the queue the longest may be removed.
 Elements are inserted at the rear (enqueued) and removed from
the front (dequeued)
Front RearQueue
D:Data StructuresHanif_SearchQueues ad5.ppt,P-23

7. 7
Queues (2/2)
 The queue supports three fundamental methods:
 New():ADT – Creates an empty queue
 Enqueue(S:ADT, o:element):ADT - Inserts object o at the rear
of the queue
 Dequeue(S:ADT):ADT - Removes the object from the front of
the queue; an error occurs if the queue is empty
 Front(S:ADT):element - Returns, but does not remove, the
front element; an error occurs if the queue is empty

8. 8
Array implementation of queues
 A queue is a first in, first out (FIFO) data structure
 This is accomplished by inserting at one end (the rear) and
deleting from the other (the front)
 To insert: put new element in location 4, and set rear to 4
 To delete: take element from location 0, and set front to 1
17 23 97 44
0 1 2 3 4 5 6 7
myQueue:
rear = 3front = 0
D:Data StructuresHanif_SearchQueues23-stacks-queues-deques.ppt

9. 9
Array implementation of queues
 Notice how the array contents “crawl” to the right as elements are
inserted and deleted
 This will be a problem after a while!
17 23 97 44 333After insertion:
23 97 44 333After deletion:
rear = 4front = 1
17 23 97 44Initial queue:
rear = 3front = 0

10. 10
Circular arrays
 We can treat the array holding the queue elements as
circular (joined at the ends)
44 55 11 22 33
0 1 2 3 4 5 6 7
myQueue:
rear = 1 front = 5
 Elements were added to this queue in the order 11, 22,
33, 44, 55, and will be removed in the same order
 Use: front = (front + 1) % myQueue.length;
and: rear = (rear + 1) % myQueue.length;

11. 11
Full and empty queues
 If the queue were to become completely full, it would look
like this:
 If we were then to remove all eight elements, making the queue
completely empty, it would look like this:
44 55 66 77 88 11 22 33
0 1 2 3 4 5 6 7
myQueue:
rear = 4 front = 5
0 1 2 3 4 5 6 7
myQueue:
rear = 4 front = 5
This is a problem!

12. 12
Full and empty queues: solutions
 Solution #1: Keep an additional variable
 Solution #2: (Slightly more efficient) Keep a gap between
elements: consider the queue full when it has n-1 elements
44 55 66 77 88 11 22 33
0 1 2 3 4 5 6 7
myQueue:
rear = 4 front = 5count = 8
44 55 66 77 11 22 33
0 1 2 3 4 5 6 7
myQueue:
rear = 3 front = 5

13. Queue Implementation using
Linked List
 Basic idea:
 Create a linked list to which items would be added to one end and deleted
from the other end.
 Two pointers will be maintained:
 One pointing to the beginning of the list (point fromwhere elements will be
deleted). <Front>
 Another pointing to the end of the list (point where new elements will be
inserted). <Rear>
13
D:Data StructuresPRG DS CS11001L9-3.pdf

14. 14
Linked-list implementation of queues
 In a queue, insertions occur at one end, deletions at
the other end
 Operations at the front of a singly-linked list (SLL)
are O(1), but at the other end they are O(n)
 Because you have to find the last element each time
 BUT: there is a simple way to use a singly-linked
list to implement both insertions and deletions in
O(1) time
 You always need a pointer to the first thing in the list
 You can keep an additional pointer to the last thing in the
list

15. 15
Enqueueing a node
17
Node to be
enqueued
To enqueue (add) a node:
Find the current last node
Change it to point to the new last node
Change the last pointer in the list header
2344
last
first
97

16. 16
Dequeueing a node
 To dequeue (remove) a node:
 Copy the pointer from the first node into the header
44 97 23 17
last
first

17. 17
Queue implementation details
 With an array implementation:
 you can have both overflow and underflow
 you should set deleted elements to null
 With a linked-list implementation:
 you can have underflow
 overflow is a global out-of-memory condition
 there is no reason to set deleted elements to null

18. Queue and Multiprogramming
(1/2)
 Multiprogramming is a way of achieving a
limited form of parallelism
 It allows to run multiple tasks or
computational threads at the same time
 E.g., one thread can be responsible for
catching mouse clicks while others can be
responsible for moving parts of animation
around in a screen canvas
E:DSALcomp202 ULPweek2[1].ppt

19. Queue and Multiprogramming
(2/2)
 When we design a program or operating system
that uses multiple threads, we must disallow an
individual thread to monopolise the CPU, in order
to avoid application or applet hanging
 One of the solutions is to utilize a queue to
allocate the CPU time to the running threads in
the round-robin protocol.

20. Application of Queues: Buffers and
Scheduling
 Important use of queues is I/O scheduling
 Use buffers in memory to improve program
execution
 Buffer arranged
in FIFO
structure
E:Data StructuresHanif_Searchchapter08.ppt

21. Application of Queues: Buffers and
Scheduling
 Consider a keyboard buffer
 Acts as a queue
 But elements may be
removed from the back of
the queue with
backspace key
 A printer spool is a queue of print jobs

22. Application of Queues: Buffers and
Scheduling
 Queues used to
schedule tasks
within an operating
system
 Job moves from disk to ready queue

23. 23
Deques
 A deque is a double-ended queue
 Insertions and deletions can occur at either end
 Implementation is similar to that for queues
 Deques are not heavily used
 You should know what a deque is, but we won’t
explore them much further
D:Data StructuresHanif_SearchQueues23-stacks-queues-deques.ppt

24. Application of Queues: Buffers and
Scheduling
 Also times when insertions, deletions must be
made from both ends
 This requires a double
ended queue
 Called a deque (pronounced "deck")
 Could also be considered a double ended stack (or
"dack")
D:Data StructuresHanif_Searchchapter08.ppt

25. Priority Queues
 Priority queues are queues in which items are ordered by priority
rather than temporally (i.e. order in which received).
 Any queue implementation then can be taken and modified to
acquire a priority queue.
 Instead of unconditionally adding to the back, the queue must be
scanned for the correct insertion point.
 An array implementation then would require shifting elements
 Hence a linked list implementation is preferred.
 A heap can be used as the underlying implementation of a priority
queue (to be discussed in heapsort algorithm).
E:Data StructuresHanif_SearchQueueschapter_05-queues.ppt

26. Application of Queues: Buffers and
Scheduling
 Ready queue may actually
be a priority queue … job may get to "cut the
line" based on its priority
D:Data StructuresHanif_Searchchapter08.ppt

27. Priority Queue
 Priority queues are often used in resource management, Event
simulation, and in the implementation of some algorithms (e.g.,
some graph algorithms, some backtracking algorithms).
 Several data structures can be used to implement priority queues.
Below is a comparison of some:
Dequeue MinFind MinEnqueueData structure
O(n)O(n)O(1)Unsorted List
O(1)O(1)O(n)Sorted List
O(log n)O(log n)O(log n)AVL Tree
O(log n)O(1)O(log n)MinHeap
D:Data StructuresICS202Lecture21.ppt+
D:Data StructuresHanif_SearchQueuesad5.ppt