The document discusses binary search trees (BSTs), including their representation as linked data structures, common operations like search, insertion, deletion, finding minimum/maximum elements, and predecessors/successors. While BST operations take O(h) time where h is the tree height, h can be as large as n for an unbalanced tree. The document thus notes that better balanced search trees like AVL trees and red-black trees are preferable to ensure O(log n) performance of operations.

1. Chapter 9
Binary Search Trees
Dr. Muhammad Hanif Durad
Department of Computer and Information Sciences
Pakistan Institute Engineering and Applied Sciences
hanif@pieas.edu.pk
Some slides have bee adapted with thanks from some other lectures
available on Internet. It made my life easier, as life is always
miserable at PIEAS (Sir Muhammad Yusaf Kakakhil )

2. Dr. Hanif Durad 2
Lecture Outline
 Binary Search Trees
 BST – Representation
 Various Operation in Binary Search Trees
 Inorder Traversal
 Tree Search
 Finding Min & Max
 Predecessor and Successor
 Insertion and Delete
 BST Problems
 Better Search Trees
IA, Chapter 12 P-251

3. Binary Search Trees-
Introduction
 View today as data structures that can support
dynamic set operations.
 Search, Minimum, Maximum, Predecessor, Successor,
Insert, and Delete.
 Can be used to build
 Dictionaries.
 Priority Queues.
 Basic operations take time proportional to the height
of the tree – O(h).
D:DSALCOMP 550-00115-btrees.ppt

4. Why BST
DeletionInsertionRetrievalData Structure
O(log n)
FAST
O(log n)
FAST
O(log n)
FAST
BST
O(n)
SLOW
O(n)
SLOW
O(log n)
FAST*
Sorted Array
O(n)
SLOW
O(n)
SLOW
O(n)
SLOW
Sorted Linked List
 BSTs provide good logarithmic time performance in the best and
average cases.
 Average case complexities of using linear data structures compared
to BSTs:
*using binary search
D:Data StructuresICS202Lecture18.ppt

5. 9.2 Binary Search Tree Property
(1/2)
 Stored keys must satisfy
the binary search tree
property.
  y in left subtree of x,
then key[y]  key[x].
  y in right subtree of x,
then key[y]  key[x].
56
26 200
18 28 190 213
12 24 27

6. 666
Binary Search Tree Property (2/2)
6
D:Data StructuresCOMP171 Data Structures and Algorithmbst.ppt

7. Binary Search Trees
A binary search tree
Not a binary search tree
D:Data StructuresCOMP171 Data Structures and Algorithmbst.ppt

8. BST – Representation
 Represented by a linked data structure of
nodes.
 root(T) points to the root of tree T.
 Each node contains fields:
 key
 left – pointer to left child: root of left subtree.
 right – pointer to right child : root of right subtree.
 p – pointer to parent. p[root[T]] = NIL (optional).
Rightleft
key
Parent
D:DSALCOMP 550-00115-btrees.ppt

9. 9.3 Various Operation in Binary
Search Trees

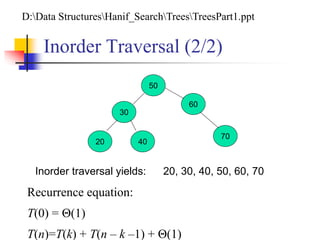
10. Inorder Traversal (1/2)
Inorder-Tree-Walk (x)
1. if x  NIL
2. then Inorder-Tree-Walk(left[p])
3. print key[x]
4. Inorder-Tree-Walk(right[p])
The binary-search-tree property allows the keys of a binary search
tree to be printed, in (monotonically increasing) order, recursively.
D:DSALCOMP 550-00115-btrees.ppt

11. Inorder Traversal (2/2)
50
70
60
30
4020
Inorder traversal yields: 20, 30, 40, 50, 60, 70
D:Data StructuresHanif_SearchTreesTreesPart1.ppt
Recurrence equation:
T(0) = Θ(1)
T(n)=T(k) + T(n – k –1) + Θ(1)

12. Querying a Binary Search Tree
 All dynamic-set search operations can be
supported in O(h) time.
 h = (lg n) for a balanced binary tree (and for
an average tree built by adding nodes in
random order.)
 h = (n) for an unbalanced tree that resembles
a linear chain of n nodes in the worst case.

13. Tree Search
Tree-Search(x, k)
1. if x = NIL or k = key[x]
2. then return x
3. if k < key[x]
4. then return Tree-Search(left[x], k)
5. else return Tree-Search(right[x], k)
Running time: O(h)
56
26 200
18 28 190 213
12 24 27
IA, P-256

14. Example: search in a binary tree
Dr. Hanif Durad 14
IA, P-257
Search for 13 in the tree

15. Iterative Tree Search
Iterative-Tree-Search(x, k)
1. while x  NIL and k  key[x]
2. do if k < key[x]
3. then x  left[x]
4. else x  right[x]
5. return x
The iterative tree search is more efficient on most computers.
The recursive tree search is more straightforward.
56
26 200
18 28 190 213
12 24 27

16. Finding Min & Max
Tree-Minimum(x) Tree-Maximum(x)
1. while left[x]  NIL 1. while right[x]  NIL
2. do x  left[x] 2. do x  right[x]
3. return x 3. return x
Q: How long do they take?
 The binary-search-tree property guarantees that:
 The minimum is located at the left-most node.
 The maximum is located at the right-most node.

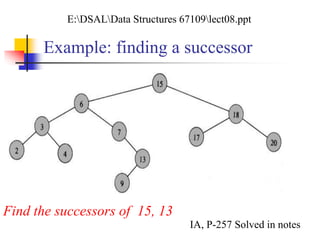
17. Predecessor and Successor
 Successor of node x is the node y such that key[y] is
the smallest key greater than key[x].
 The successor of the largest key is NIL.
 Search consists of two cases.
 If node x has a non-empty right subtree, then x’s successor is
the minimum in the right subtree of x.
 If node x has an empty right subtree, then:
 As long as we move to the left up the tree (move up through right
children), we are visiting smaller keys.
 x’s successor y is the node that x is the predecessor of (x is the
maximum in y’s left subtree).
 In other words, x’s successor y, is the lowest ancestor of x whose left
child is also an ancestor of x.

18. Pseudo-code for Successor
Code for predecessor is symmetric.
Running time: O(h)
56
26 200
18 28 190 213
12 24 27
Tree-Successor(x)
 if right[x]  NIL
2. then return Tree-Minimum(right[x])
3. y  p[x]
4. while y  NIL and x = right[y]
5. do x  y
6. y  p[y]
7. return y

19. Example: finding a successor
Find the successors of 15, 13
IA, P-257 Solved in notes
E:DSALData Structures 67109lect08.ppt

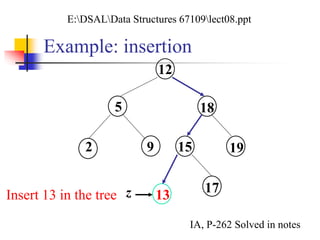
20. BST Insertion – Pseudocode
Tree-Insert(T, z)
1. y  NIL
2. x  root[T]
3. while x  NIL
4. do y  x
5. if key[z] < key[x]
6. then x  left[x]
7. else x  right[x]
8. p[z]  y
9. if y = NIL
10. then root[t]  z
11. else if key[z] < key[y]
12. then left[y]  z
13. else right[y]  z
 Change the dynamic set
represented by a BST.
 Ensure the binary-search-
tree property holds after
change.
 Insertion is easier than
deletion.
56
26 200
18 28 190 213
12 24 27

21. Analysis of Insertion
 Initialization: O(1)
 While loop in lines 3-7
searches for place to
insert z, maintaining
parent y.
This takes O(h) time.
 Lines 8-13 insert the
value: O(1)
 TOTAL: O(h) time to
insert a node.
Tree-Insert(T, z)
1. y  NIL
2. x  root[T]
3. while x  NIL
4. do y  x
5. if key[z] < key[x]
6. then x  left[x]
7. else x  right[x]
8. p[z]  y
9. if y = NIL
10. then root[t]  z
11. else if key[z] < key[y]
12. then left[y]  z
13. else right[y]  z

22. Example: insertion
12
5
9
18
1915
17
2
13Insert 13 in the tree z
IA, P-262 Solved in notes
E:DSALData Structures 67109lect08.ppt

23. Exercise: Sorting Using BSTs
Sort (A)
for i  1 to n
do tree-insert(A[i])
inorder-tree-walk(root)
 What are the worst case and best case running times?
 In practice, how would this compare to other sorting
algorithms?

24. Answers to Exercise: Sorting
Using BSTs
 Analysis
 Each item’s insertion takes O(logN)
 N times- O(N*logN) or O(N2)
 Traversal O(N)
Printed as 5A

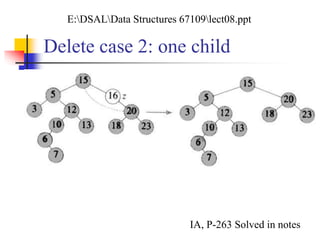
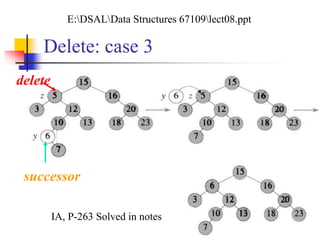
25. Tree-Delete (T, x)
if x has no children  case 0
then remove x
if x has one child  case 1
then make p[x] point to child
if x has two children (subtrees)  case 2
then swap x with its successor
perform case 0 or case 1 to delete it
 TOTAL: O(h) time to delete a node

26. Deletion – Pseudocode (1/2)
Tree-Delete(T, z)
/* Determine which node to splice out: either z or z’s successor. */
 if left[z] = NIL or right[z] = NIL
 then y  z
 else y  Tree-Successor[z]
/* Set x to a non-NIL child of x, or to NIL if y has no children. */
4. if left[y]  NIL
5. then x  left[y]
6. else x  right[y]
/* y is removed from the tree by manipulating pointers of p[y] and x */
7. if x  NIL
8. then p[x]  p[y]
/* Continued on next slide */

27. Deletion – Pseudocode (2/2)
Tree-Delete(T, z) (Contd. from previous slide)
9. if p[y] = NIL
10. then root[T]  x
11. else if y  left[p[i]]
12. then left[p[y]]  x
13. else right[p[y]]  x
/* If z’s successor was spliced out, copy its data into z */
14. if y  z
15. then key[z]  key[y]
16. copy y’s satellite data into z.
17. return y

28. Delete case 1: no children!
IA, P-263Solved in notes
E:DSALData Structures 67109lect08.ppt

29. Delete case 2: one child
IA, P-263 Solved in notes
E:DSALData Structures 67109lect08.ppt

30. Delete: case 3
successor
delete
IA, P-263 Solved in notes
E:DSALData Structures 67109lect08.ppt

31. Inefficiency of general BSTs
 All operations in BST are performed in time
O(h), where h is the height of BST
 Unfortunately h might be as large as n, e.g.,
after n consecutive insertions of elements with
keys in increasing order
 The advantages of the binary search (O(log n)
time update) might be lost if BST is not
balanced
E:DSALcomp202 ULPweek3[1].ppt

32. BST Problems
Same entries, different insertion sequence:
 Not good! Would like to keep tree balanced.
D:Data StructuresHanif_SearchTrees2-3Trees.ppt

33.  Prevent the degeneration of the BST :
 A BST can be set up to maintain balance during
updating operations (insertions and removals)
 Types of ST which maintain the optimal performance:
 splay trees
 AVL trees
 2-4 Trees
 Red-Black trees
 B-trees
Better Search Trees
E:Data StructuresCSCE3110BinarySearchTrees.ppt