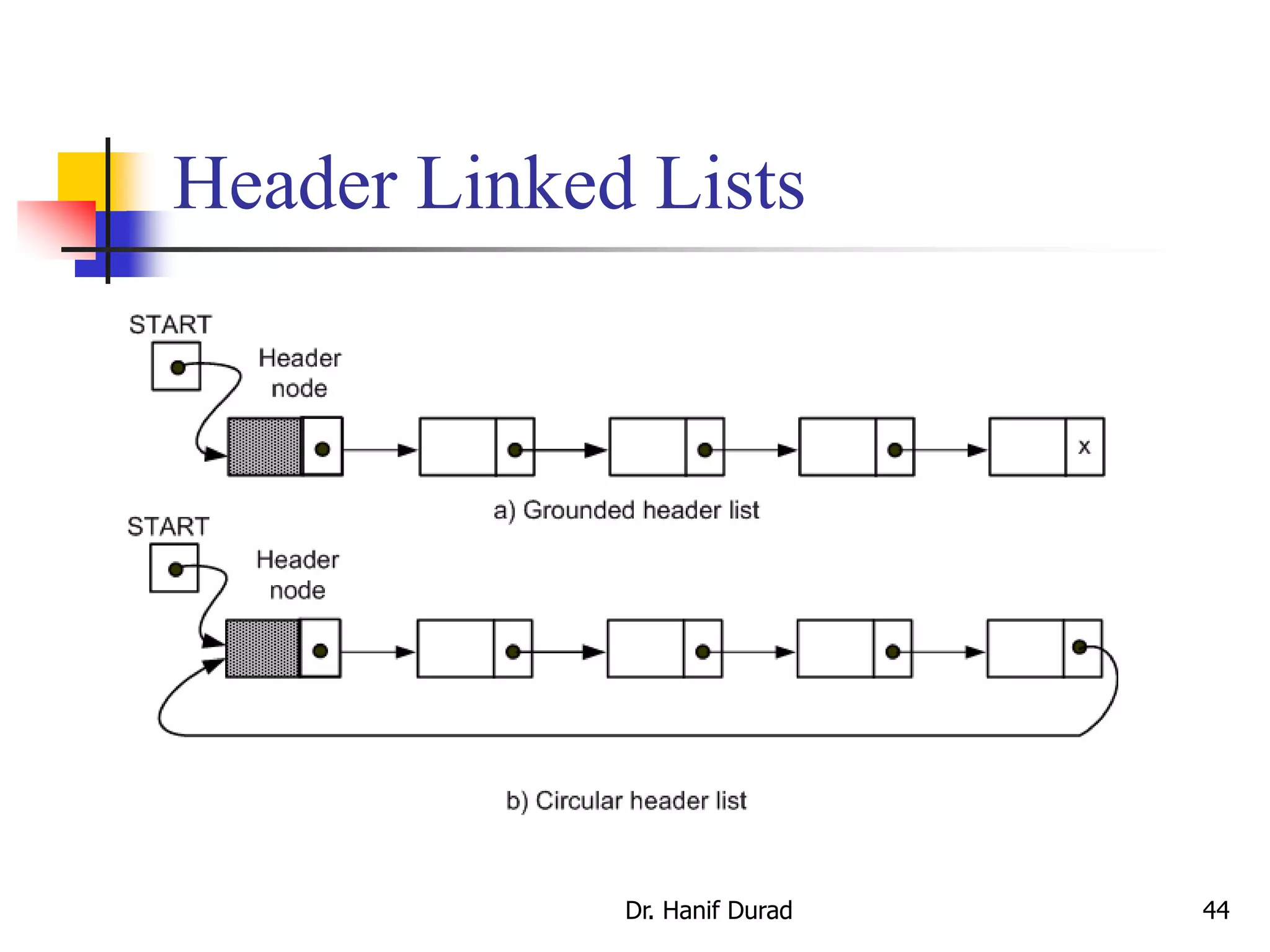
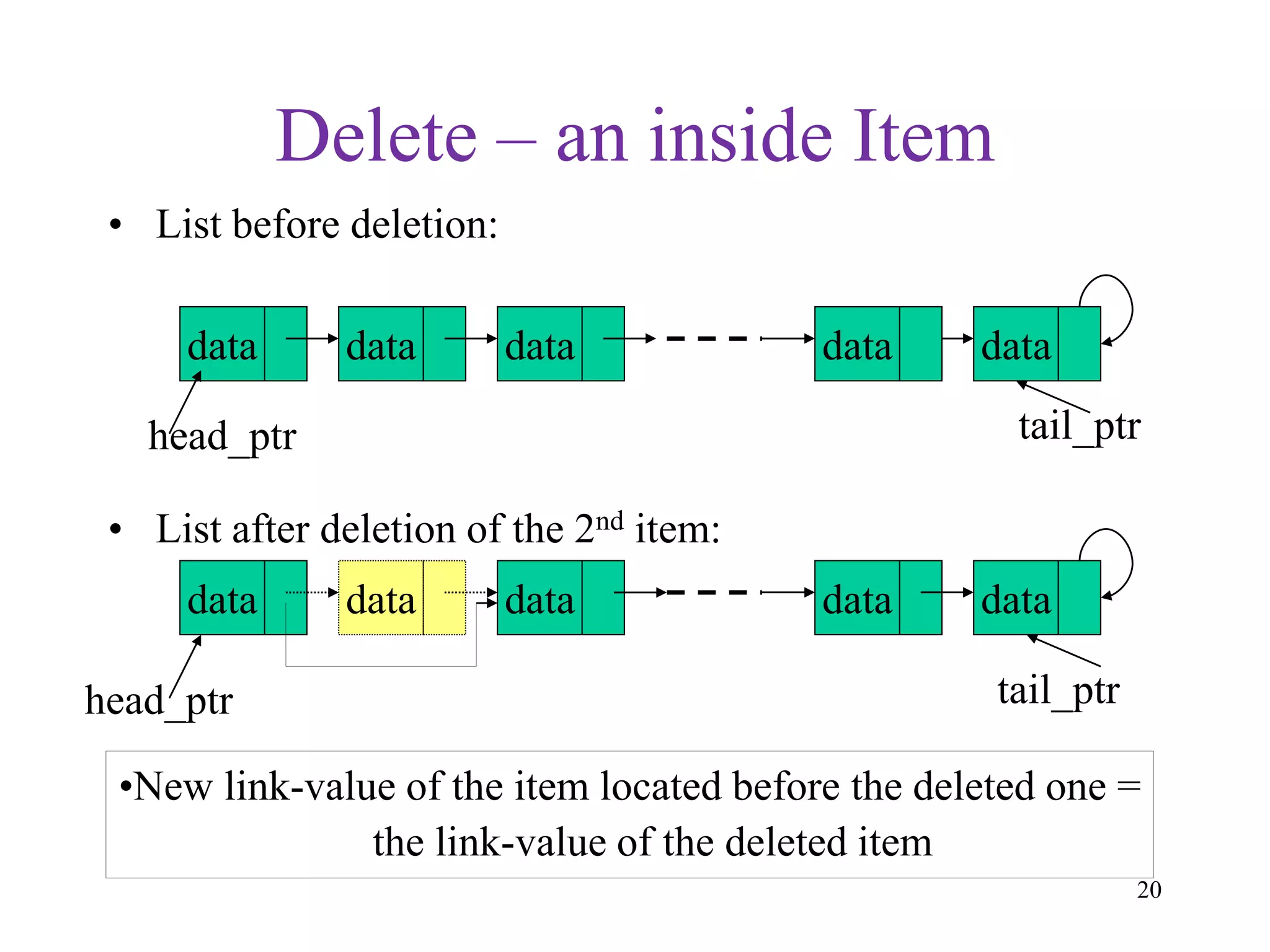
The document outlines the key concepts of linked lists including: - Linked lists allow for dynamic resizing and efficient insertion/deletion unlike arrays. - A linked list contains nodes that have a data field and a pointer to the next node. - Common operations on linked lists include insertion, deletion, searching, and traversing the list. - The time complexity of these operations depends on whether it's at the head, tail, or interior node. - Linked lists can be implemented using classes for the node and linked list objects.

1. Chapter 5
Linked Lists
Dr. Muhammad Hanif Durad
Department of Computer and Information Sciences
Pakistan Institute Engineering and Applied Sciences
hanif@pieas.edu.pk
Some slides have bee adapted with thanks from some other lectures
available on Internet. It made my life easier, as life is always
miserable at PIEAS (Sir Muhammad Yusaf Kakakhil )

2. Dr. Hanif Durad 2
Lecture Outline
 Abstract Data Types (ADTs)
 Arrays: pluses and minuses
 Singly Linked Lists
 Examples of Linked Lists
 Operations on Linked Lists
 Header Linked Lists
 Circular Linked Lists
 Doubly Linked Lists
 The Polynomial ADT

3. 33
Primitive Data Type vs. Abstract
Data Types
data
programmer
Primitive DT:
programmer
ADT:
Interface (API)
Implementation
(methods)
Data
D:Data StructuresCPT S 223adt.ppt

4. 44
Abstract Data Types (ADTs)
 ADT is a set of objects together with a set of operations.
 “Abstract” in that implementation of operations not specified in ADT
definition
 E.g., List
 Insert, delete, search, sort
 C++ class perfect for ADTs
 Can change ADT implementation details without breaking code
using ADT
4

5. Arrays: pluses and minuses
 + Fast element access.
 -- Impossible to resize.
 Many applications require resizing!
 Required size not always immediately
available.
Dr. Hanif Durad 5
D:Data StructuresHanif_SearchLinked ListsLinkedLists.ppt, P-1

6. Arrays: pluses and minuses
 To insert or remove an element at an interior location in an
Array requires shifting of data and is an O(n) operation.
6
D:Data StructuresHanif_SearchLinked Lists 10. Linked Lists.ppt, P-2

7. Definition of Singly Linked Lists
 A linked list is a sequence of items (objects)
where every item is linked to the next.
 Graphically:
data data data data
head_ptr tail_ptr
D:Data StructuresHanif_SearchLinked Lists lecture6.ppt, P-2

8. 8
Definition Details
 Each item has a data part (one or more data
members), and a link that points to the next item
 One natural way to implement the link is as a
pointer; that is, the link is the address of the next
item in the list
 It makes good sense to view each item as an object,
that is, as an instance of a class.
 We call that class: Node
 The last item does not point to anything. We set its
link member to NULL. This is denoted graphically
by a self-loop

9. 9
Examples of Linked Lists
(A Waiting Line)
 A waiting line of customers: John, Mary, Dan,
Sue (from the head to the tail of the line)
 A linked list of strings can represent this line:
John Mary Dan Sue
head_ptr
tail_ptr

10. 10
Examples of Linked Lists
(A Stack of Numbers)
 A stack of numbers (from top to bottom):
10, 8, 6, 8, 2
 A linked list of ints can represent this stack:
10 8 6 2
head_ptr tail_ptr
8

11. 11
Examples of Linked Lists
(A Set of Non-redundant Elements)
 A set of characters: a, b, d, f, c
 A linked list of chars can represent this set:
a b d c
head_ptr tail_ptr
f

12. 12
Examples of Linked Lists
(A Sorted Set of Non-redundant Elements)
 A set of characters: a, b, d, f, c
 The elements must be arranged in sorted
order: a, b, c, d, f
 A linked list of chars can represent this set:
a b c f
head_ptr tail_ptr
d

13. 13
Examples of Linked Lists
(A Polynomial)
 A polynomial of degree n is the function
Pn(x)=a0+a1x+a2x2+…+anxn. The ai’s are called
the coefficients of the polynomial
 The polynomial can be represented by a linked
list (2 data members and a link per item):
a0,0 a1,1 a2,2 an,n
head_ptr tail_ptr

14. 14
Operations on Linked Lists
 Insert a new item
 At the head of the list, or
 At the tail of the list, or
 Inside the list, in some designated position
 Search for an item in the list
 The item can be specified by position, or by some value
 Delete an item from the list
 Search for and locate the item, then remove the item,
and finally adjust the surrounding pointers
 size( );
 isEmpty( )

15. 15
Insert– At the Head
• Insert a new data A. Call new: newPtr
List before insertion:
• After insertion to head:
data data data data
head_ptr tail_ptr
A
data data data data
head_ptr tail_ptr
A
•The link value in the new item = old head_ptr
•The new value of head_ptr = newPtr

16. 16
Insert – at the Tail
• Insert a new data A. Call new: newPtr
List before insertion
• After insertion to tail:
data data data data
head_ptr tail_ptr
A
data data data data
head_ptr tail_ptr
A
•The link value in the new item = NULL
•The link value of the old last item = newPtr

17. 17
Insert – inside the List
• Insert a new data A. Call new: newPtr
List before insertion:
• After insertion in 3rd position:
data data data data
head_ptr tail_ptr
data
data A data data
head_ptr
tail_ptr
data
•The link-value in the new item = link-value of 2nd item
•The new link-value of 2nd item = newPtr

18. 18
Delete – the Head Item
• List before deletion:
• List after deletion of the head item:
data data data data
head_ptr tail_ptr
data data data data
head_ptr tail_ptr
data
•The new value of head_ptr = link-value of the old head item
•The old head item is deleted and its memory returned
data

19. 19
Delete – the Tail Item
• List before deletion:
• List after deletion of the tail item:
data data data data
head_ptr
tail_ptr
data data data
head_ptr tail_ptr
•New value of tail_ptr = link-value of the 3rd from last item
•New link-value of new last item = NULL.
data
datadata

20. 20
Delete – an inside Item
• List before deletion:
• List after deletion of the 2nd item:
data data data data
head_ptr tail_ptr
data data
head_ptr tail_ptr
•New link-value of the item located before the deleted one =
the link-value of the deleted item
data
data datadata

21. 21
size() and isEmpty()
 We need to scan the items in the list from the head_ptr
to the last item marked by its link-value being NULL
 Count the number of items in the scan, and return the
count. This is the size().
 Alternatively, keep a counter of the number of item,
which gets updated after each insert/delete. The function
size( ) returns that counter
 If head_ptr is NULL, isEmpty() returns true; else, it
returns false.

22. 22
Searching for an Item
 Suppose you want to find the item whose data value is A
 You have to search sequentially starting from the head
item rightward until the first item whose data member is
equal to A is found.
 At each item searched, a comparison between the data
member and A is performed.

23. CS 103 23
Time of the Operations
 Time to search() is O(L) where L is the relative
location of the desired item in the List. In the worst
case. The time is O(n). In the average case it is
O(N/2)=O(n).
 Time for remove() is dominated by the time for
search, and is thus O(n).
 Time for insert at head or at tail is O(1).
 Time for insert at other positions is dominated by
search time, and thus O(n).
 Time for size() is O(1), and time for isEmpty() is O(1)

24. Implementation
Notes
Dr. Hanif Durad 24

25. 25
Implementation of an Item
 Each item is a collection of data and pointer
fields, and should be able to support some basic
operations such as changing its link value and
returning its member data
 Therefore, a good implementation of an item is a
class
 The class will be called Node

26. 26
Class Node Design for Item
 The member variables of Node are:
 The data field(s)
 The link pointer, which will be called next
 The functions are:
Function Action Why Needed
getNext( ) returns the link. for navigation
getData( ) returns the data for search
setNext(Node *ptr) sets link to ptr for insert/delete
setData(type x) sets data to x. to modify data
contents

27. 27
Class Node Type
 class Node {
private:
int data; // different data type for other apps
Node *next; // the link pointer to next item
public:
Node(int x=0;Node * ptr=NULL); // constructor
int getData( );
Node *getNext( );
void setData(int x);
void setNext(Node *ptr);
};

28. 28
Class Node Implementation
 Node::Node(int x, Node *p){ data=x; next=p;};
 int Node::getData( ){return data;};
 Node * Node::getNext( ){return next;};
 void Node::setData(int x) {data=x;};
 void Node::setNext(Node *ptr){next=ptr;};

29. 29
Implementation of Linked List
 A linked list is a collection of Node objects, and
must support a number of operations
 Therefore, it is sensible to implement a linked list
as a class
 The class name for it is List

30. 30
Class Design for List
 The member variables are:
 Node *head_ptr; Node *tail_ptr;
 int numOfItems;
 Member functions
 Node * search(int x); Node * itemAt(int position);
 void removeHead(); void removeTail();
void remove(int x);
 void insertHead(int x); void insertTail(int x);
void insert(Node *p, int x) // inserts item after the item
// pointed to by p
 int size( ); Node *getHead( ); Node getTail( );
 bool isEmpty( );

31. 31
Class List Type
 class List {
private:
Node *head_ptr; Node *tail_ptr; int numOfItems;
public:
List( ); // constructor
int size( ); Node *getHead( ); Node *getTail( );
bool isEmpty( );
Node *search(int x); Node *itemAt(int position);
void removeHead(); void removeTail();
void remove(int x); // delete leftmost item having x
void insertHead(int x); void insertTail(int x);
void insert(Node *p, int x);
};

32. 32
Implementation of Class List
 List::List( ){head_ptr= NULL; tail_ptr=NULL;
numOfItems=0;};
 int List::size( ){return numOfItems;};
 Node * List::getHead( ) {return head_ptr;};
 Node * List::getTail( ) {return tail_ptr;};
 bool List::isEmpty() {return (numOfItem==0);};

33. 33
Implementation of search( )
 Node *List::search(int x){
Node * currentPtr = getHead( );
while (currentPtr != NULL){
if (currentPtr->getData( ) == x)
return currentPtr;
else
currentPtr = currentPtr->getNext();
}
return NULL; // Now x is not, so return NULL
};

34. 34
Implementation of itemAt( )
 Node *List::itemAt(int position){
if (position<0 || position>=numOfItems)
return NULL;
Node * currentPtr = getHead( );
for(int k=0;k != position; k++)
currentPtr = currentPtr -> getNext( );
return currentPtr;
};

35. 35
Implementation of removeHead( )
 void List::removeHead( ){
if (numOfItems == 0)
return;
Node * currentPtr = getHead( );
head_ptr=head_ptr->getNext( );
delete currentPtr;
numOfItems--;
};

36. 36
Implementation of removeTail( )
 void List::removeTail( ){
if (numOfItems == 0)
return;
if (head_ptr == tail_ptr){
head_ptr=NULL; tail_ptr= NULL;
numOfItems=0; return; }
Node * beforeLast = itemAt(numOfItems-2);
beforeLast->setNext(NULL); // beforeLast becomes last
delete tail_ptr; // deletes the last object
tail_ptr=beforeLast;
numOfItems--;
};

37. 37
Implementation of remove( )
 void List::remove(int x){
if (numOfItems == 0) return;
if (head_ptr==tail_ptr && head_ptr->getData()==x){
head_ptr=NULL; tail_ptr= NULL; numOfItems=0; return; }
Node * beforePtr=head_ptr; // beforePtr trails currentPtr
Node * currentPtr=head_ptr->getNext();
Node * tail = getTail();
while (currentPtr != tail)
if (currentPtr->getData( ) == x){ // x is found. Do the bypass
beforePtr->setNext(currentPtr->getNext());
delete currentPtr; numOfItems--; }
else { // x is not found yet. Forward beforePtr & currentPtr.
beforePtr = currentPtr;
currentPtr = currentPtr->getNext(); }

38. 38
Implementation of insertHead( )
 void List::insertHead(int x){
Node * newHead = new Node(x,head_ptr);
head_ptr= newHead;
if (tail_ptr == NULL) // only one item in list
tail_ptr = head_ptr;
numOfItems++;
};

39. 39
Implementation of insertTail( )
 void List::insertTail(int x){
if (isEmpty())
insertHead(x);
else{
Node * newTail = new Node(x);
tail_ptr->setNext(newTail);
tail_ptr = newTail; numOfItems++;
}
};

40. 40
Implementation of insert( )
 // inserts item x after the item pointed to by p
 void List::insert(Node *p, int x){
Node *currentPtr = head_ptr;
while(currentPtr !=NULL && currentPtr != p)
currentPtr = currentPtr->getNext();
if (currentPtr != NULL ) { // p is found
Node *newNd=new Node(x,p->getNext());
p->setNext(newNd);
numOfItems++;
}
};

41. Header Linked Lists
Dr. Hanif Durad 41

42. Dummy Head Nodes
 Dummy head node
 Always present, even when the linked list is empty
 Insertion and deletion algorithms initialize prev to
reference the dummy head node, rather than NULL
D:Data StructuresHanif_Search LL04.ppt, P-31/39

43. Header Linked Lists
 A header linked list is a linked list which always contains a
special node, called the header or sentinel node, at the beginning
of the list. The following are two widely used header lists:
 A grounder header list is a header list where the last node contains
the null pointer.
 A circular header list where the last node points back to the header
node.
 The header record may also be used to store information about the
entire file.
Dr. Hanif Durad 43
D:Data StructuresHanif_Search Data+Structures2.ppt, P-9 & 11

44. Header Linked Lists
Dr. Hanif Durad 44

45. Circular Linked Lists
 Last node references the first node
 Every node has a successor
 No node in a circular linked list contains NULL
D:Data StructuresHanif_SearchLL 04.ppt, P-30/39

46. Circular Linked Lists
 Last node references the first node
 Every node has a successor
 No node in a circular linked list contains NULL

47. Doubly Linked
Lists
Dr. Hanif Durad 47

48. Doubly linked list
 A linked list is a data structure in which the objects are arranged
in linear order
 The order in a linked list is determined by pointers in each object
 Doubly linked list
 Each element is an object with a key field and two other pointer fields:
next and prev, among other satellite fields. Given an element x
 next[x] points to its successor
 if x is the last element (called tail), next[x] = NIL
 prev[x] points to its predecessor
 if x is the first element (called head), prev[x] = NIL
 An attribute head[L] points to the first element of the list
 if head[L] = NIL, the list is empty
D:DSAL5165 Advanced Algorithm and Programming Languageunit09.ppt

49. Doubly linked list
 Singly linked list: omit the prev pointer in each
element
 Sorted linked list: the linear order of the list
corresponds to the linear order of keys stored in
elements of the list
 The minimum element is the head
 The maximum element is the tail
 Circular linked list: the prev pointer of the head points
to the tail, and the next pointer of the tail points to the
head

50. Illustration of A Doubly Linked
List
NIL

51. Searching A Linked List
 LIST-SEARCH(L, k): finds the first element with key k in list L
by a simple linear search, returning a pointer to this element
 If no object with key k appears in the list, then NIL is
returned

52. Illustration of LIST-SEARCH
head[L] 9/ 16 4 1 /
x
LIST-SEARCH(L, 4)
x x
x  head[L]while x  NIL and key[x]  4x  next[x]while x  NIL and key[x]  4x  next[x]while x  NIL and key[x]  4
return x
How about LIST-SEARCH(L, 7)?

53. Inserting Into A Linked List
 LIST-INSERT(L, x): given an element
pointed by x, splice x onto the front of the
linked list

54. Illustration of LIST-INSERT
head[L] 9/ 16 4 1 /
x 25/ next[x]head[L]prev[head[L]]  xhead[L]  xprev[x]  NIL
LIST-INSERT(L, x)

55. Deleting From A Linked List
 LIST-DELETE(L, x): given an element
pointed by x, remove x from the linked list

56. Illustration of LIST-DELETE
head[L]
9/ 16 4 1 /25/
x
next[prev[x]]  next[x]
prev[x] next[x]
LIST-DELETE(L, x)
prev[next[x]]  prev[x]
Need garbage collection for x

57. Linked Lists and
Polynomials
Dr. Hanif Durad 57
D:Data StructuresCOMP171 Data Structures and Algorithmlist.ppt

58. Example: The Polynomial ADT
 An ADT for single-variable polynomials
 Array implementation


N
i
i
i xaxf
0
)(

59. The Polynomial ADT
 Acceptable if most of the coefficients Aj are
nonzero, undesirable if this is not the case
 E.g. multiply
 most of the time is spent multiplying zeros and stepping
through nonexistent parts of the input polynomials
51123)(
1510)(
14921990
2
141000
1


xxxxP
xxxP

60. The Polynomial ADT…
 Each term is contained in one cell, and the cells are
sorted in decreasing order of exponents
coef expon link

61. 3 14 2 8 1 0
a
8 14 -3 10 10 6
b
11 14
d
a->expon == b->expon
3 14 2 8 1 0
a
8 14 -3 10 10 6
b
11 14
d
a->expon < b->expon-3 10
Adding Polynomials (1/2)
Morelists.ppt,6/24

62. 3 14 2 8 1 0
a
8 14 -3 10 10 6
b
11 14
a->expon > b->expon
-3 10
d
2 8
Adding Polynomials (2/2)